三角
三角学 释文见 2 页。
三角 即“三角学”。
球面三角 见“三角学”。
角度
平面角的大小。角度的度量制有多种,常见的有六十分制:周角的三百六十分之一称为一度,一度的六十分之一称为一分,一分的六十分之一称为一秒。度、分、秒分别用记号°、′、″表示,例如,3 度40 分 15 秒记作 3°40′15″。另一种是弧度制:当圆周上某段圆弧的弧长等于该圆的半径时,称此圆弧所对的圆心角为一“弧度”,常用符号rad表示。中国古代称之为“弪”。周角等于 2
 弧度。一弧度约等于57.296°,即 57°17′45″。
弧度。一弧度约等于57.296°,即 57°17′45″。
弧度 见“角度”。
弪 “弧度”的古称。见“角度”。
仰角 在同一铅垂面内,当视线在水平线上方时,视线与水平线的夹角。
俯角 在同一铅垂面内,当视线在水平线下方时,视线与水平线的夹角。
象限角 某一方向线与磁针方向线(南北向)之间所夹的锐角,称为此方向的“象限角”。以指北方向或指南方向起向两旁计算,用北偏东、北偏西或南偏东、南偏西几度来表示。如图,OA的方向是北偏东 30°,OB的方向是南偏西 60°。
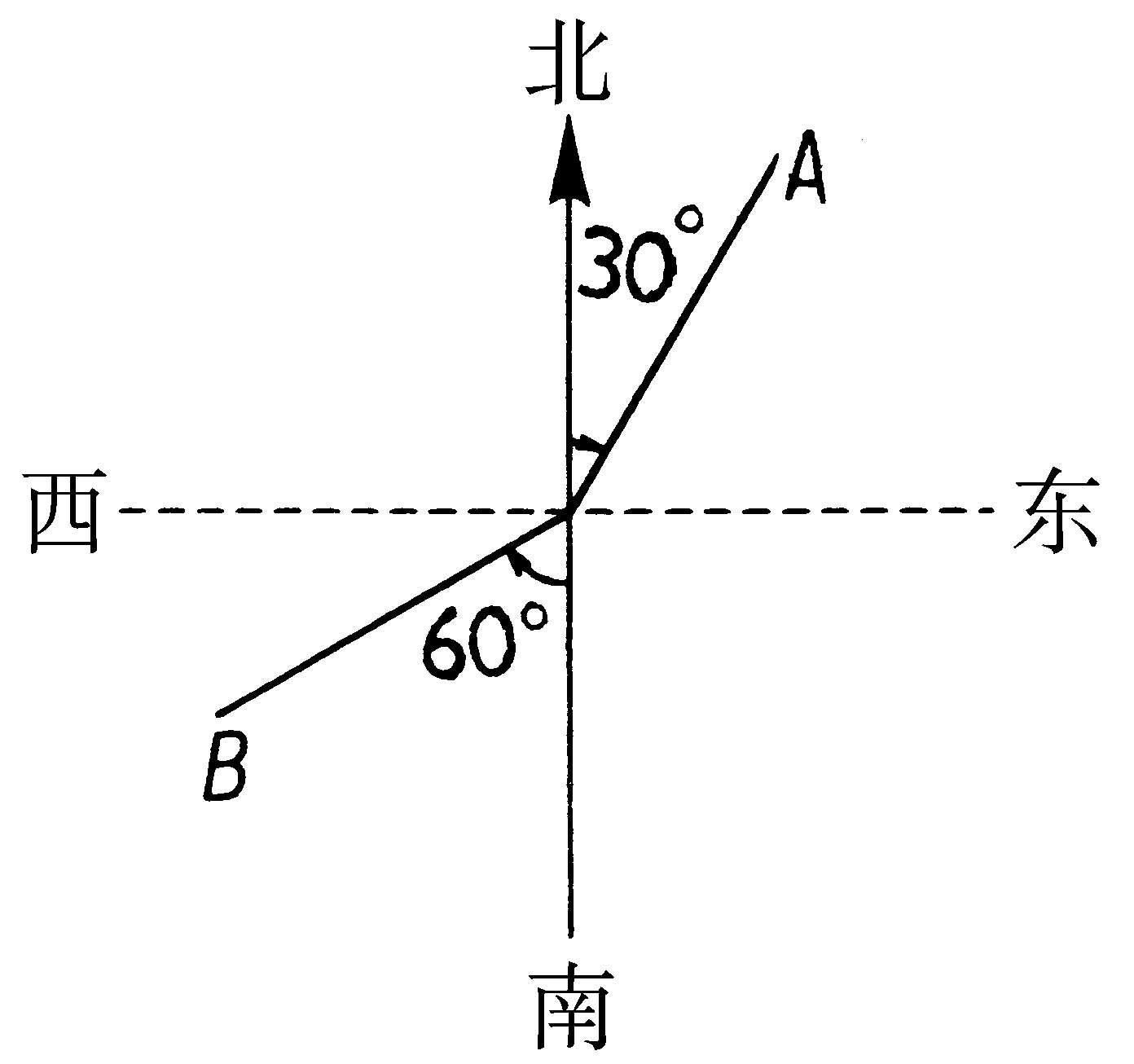
象限角
方位角 某一方向线与指北方向线之间的夹角,称为此方向的“方位角”。以指北方向线起按顺时针方向计算,在 0° ~ 360°之间。如图,OA的方向是方位角 30°,OB的方向是方位角
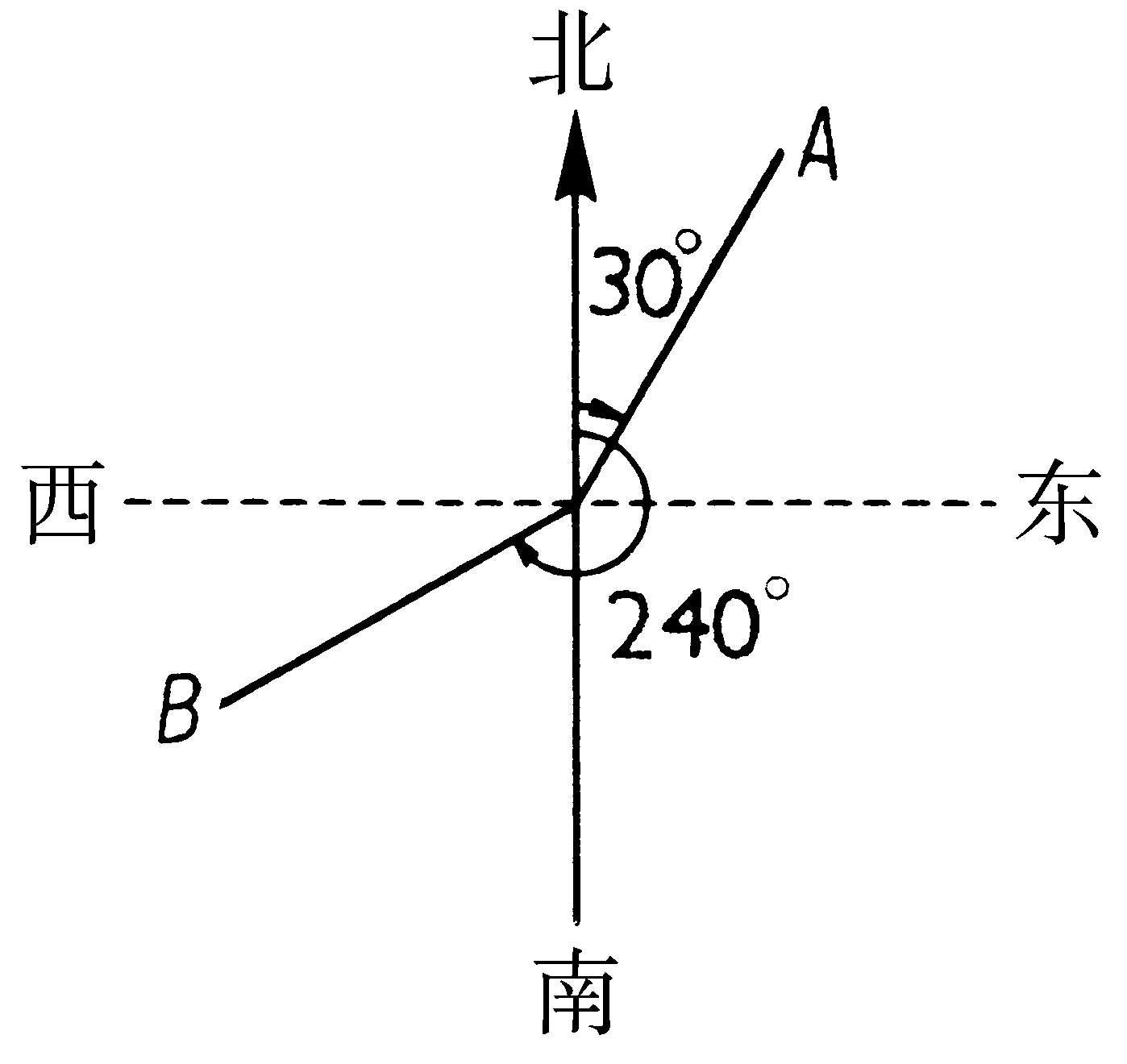
方位角
三角函数
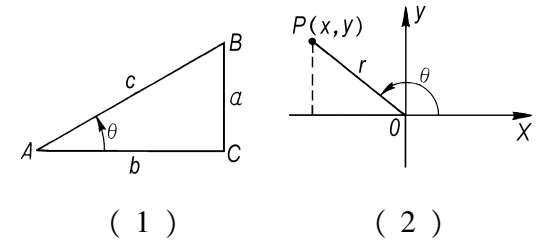
设以θ为一锐角的直角三角形的三边为a、b、c(81 页图 1 ),比
 分别称为角θ的正弦、余弦、正切、余切、正割、余割,并依次记为sinθ、 cosθ、 tanθ(或tgθ)、 cotθ(或ctgθ)、secθ、 cscθ(或cosecθ)。当θ变化时,它们都随之而变化,因而每一个都是θ的函数,称为“三角函数”。有时用到 1 -cosθ,称为θ的“正矢”,记为versθ;1 - sinθ称为θ的“余矢”,记为coversθ。还可以用坐标法把三角函数的概念推广到任意角。在平面上引进直角坐标系,对于任意角θ,顶点在原点O,一边沿正实轴,在角的另一边上任取一点P(x,y),P到O的距离为
分别称为角θ的正弦、余弦、正切、余切、正割、余割,并依次记为sinθ、 cosθ、 tanθ(或tgθ)、 cotθ(或ctgθ)、secθ、 cscθ(或cosecθ)。当θ变化时,它们都随之而变化,因而每一个都是θ的函数,称为“三角函数”。有时用到 1 -cosθ,称为θ的“正矢”,记为versθ;1 - sinθ称为θ的“余矢”,记为coversθ。还可以用坐标法把三角函数的概念推广到任意角。在平面上引进直角坐标系,对于任意角θ,顶点在原点O,一边沿正实轴,在角的另一边上任取一点P(x,y),P到O的距离为
 (图 2)。角θ的三角函数定义如下:
(图 2)。角θ的三角函数定义如下:

三角函数具有周期性,是重要的周期函数。
正弦 三角函数之一。
余弦 三角函数之一。
正切 三角函数之一。
余切 三角函数之一。
正割 三角函数之一。
余割 三角函数之一。
八线 中国旧时称三角函数为“八线”,因八个三角函数值可以用图中八条线段表示,即
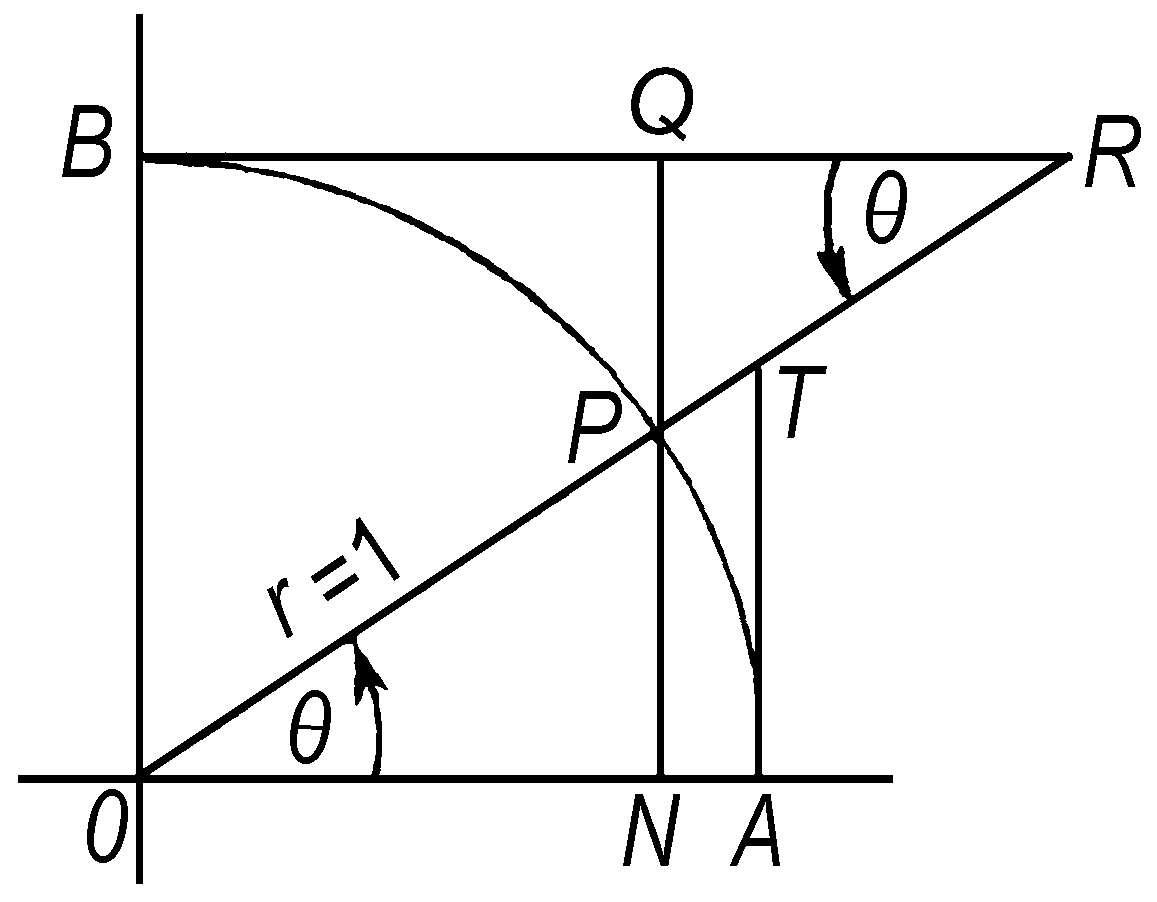
八 线
这里
 为第一象限的单位圆周(圆半径r= 1)。
为第一象限的单位圆周(圆半径r= 1)。
正弦曲线
正弦函数y= sinx的图形。由于正弦函数是周期为 2
 的周期函数,所以这条曲线是由图中从 0 到 2
的周期函数,所以这条曲线是由图中从 0 到 2
 这一段,重复地向左右两方无限延伸而得的。
这一段,重复地向左右两方无限延伸而得的。

正弦曲线
余弦曲线
余弦函数y= cosx的图形。由于余弦函数是周期为 2
 的周期函数,所以这条曲线是由图中从 0到 2
的周期函数,所以这条曲线是由图中从 0到 2
 这一段,重复地向左右两方无限延伸而得的。
这一段,重复地向左右两方无限延伸而得的。

余弦曲线
正切曲线
正切函数y= tanx的图形。由于正切函数是周期为
 的周期函数,所以它的图像是把图中从
的周期函数,所以它的图像是把图中从
 到
到
 一支分别接连向左及右平行移动距离
一支分别接连向左及右平行移动距离
 而得。
而得。

正切曲线
反三角函数
三角函数的反函数。是多值函数。它们是反正弦arcsinx、反余弦arccosx、反正切arctanx、反余切arccotx、反正割arcsecx、反余割arccscx等。各表示其正弦、余弦、正切、余切、正割、余割为x的角。往往对反三角函数的值加以限制,使之成为单值函数,将反正弦函数的值y限在
 ,称y为反正弦函数的主值,记为y= arcsinx;相应地,反余弦函数的主值y= arccosx,限在 0≤y≤
,称y为反正弦函数的主值,记为y= arcsinx;相应地,反余弦函数的主值y= arccosx,限在 0≤y≤
 ;反正切函数的主值y= arctanx,限在
;反正切函数的主值y= arctanx,限在
 ;反余切函数的主值y=arccotx,限在 0 <y<
;反余切函数的主值y=arccotx,限在 0 <y<
 。
。
加法定理 两角和或差的三角函数公式的统称。如
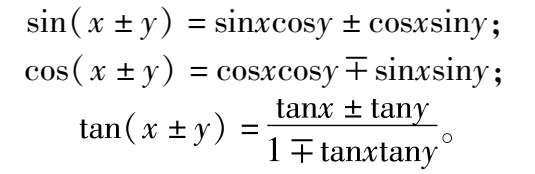
加法定理是三角公式的基础公式,倍角、半角及和差化积等公式都可由此推出。
倍角公式 用角x的三角函数来表示角2x的三角函数的公式。如
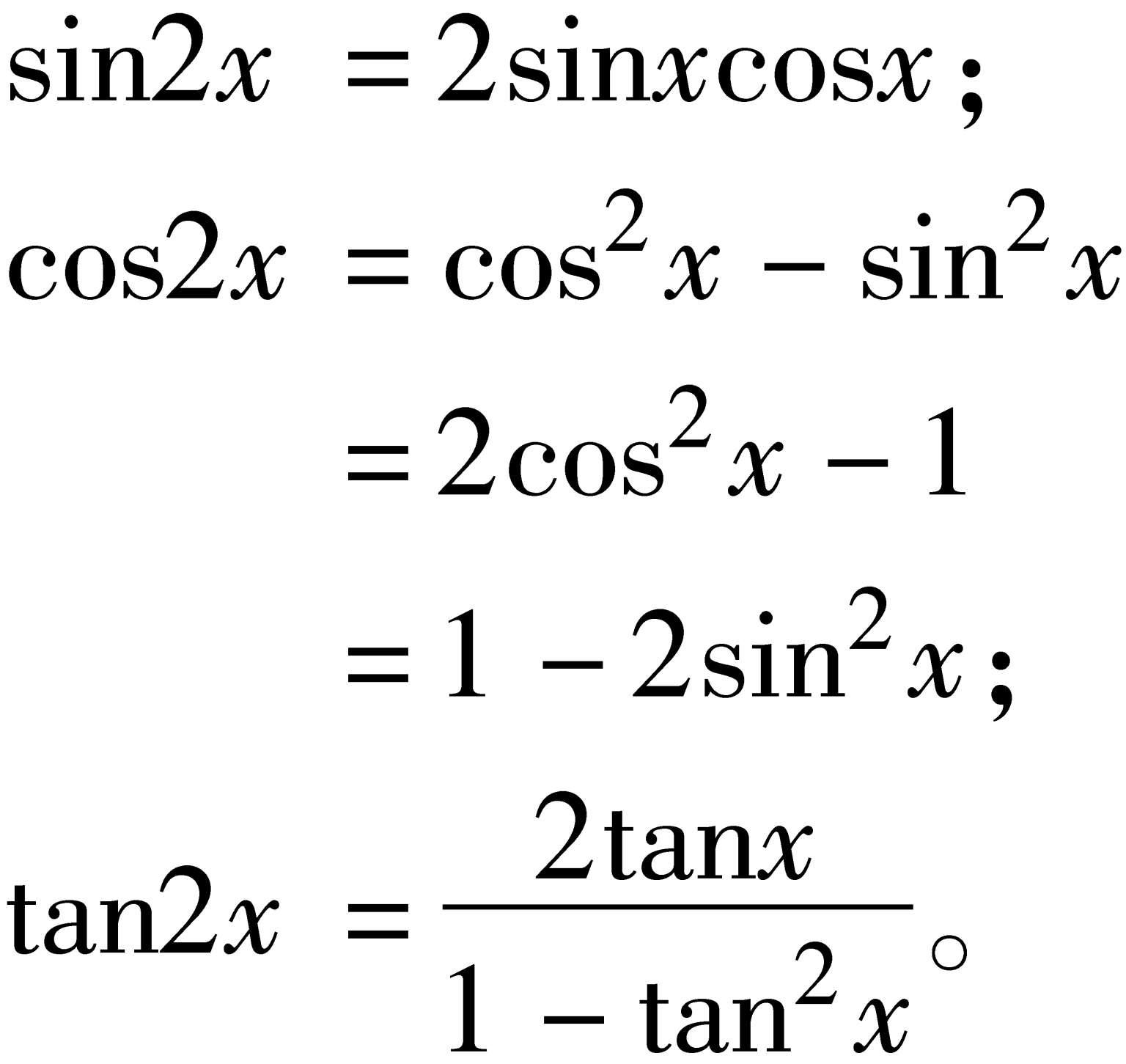
相应地,双曲函数的倍角公式有
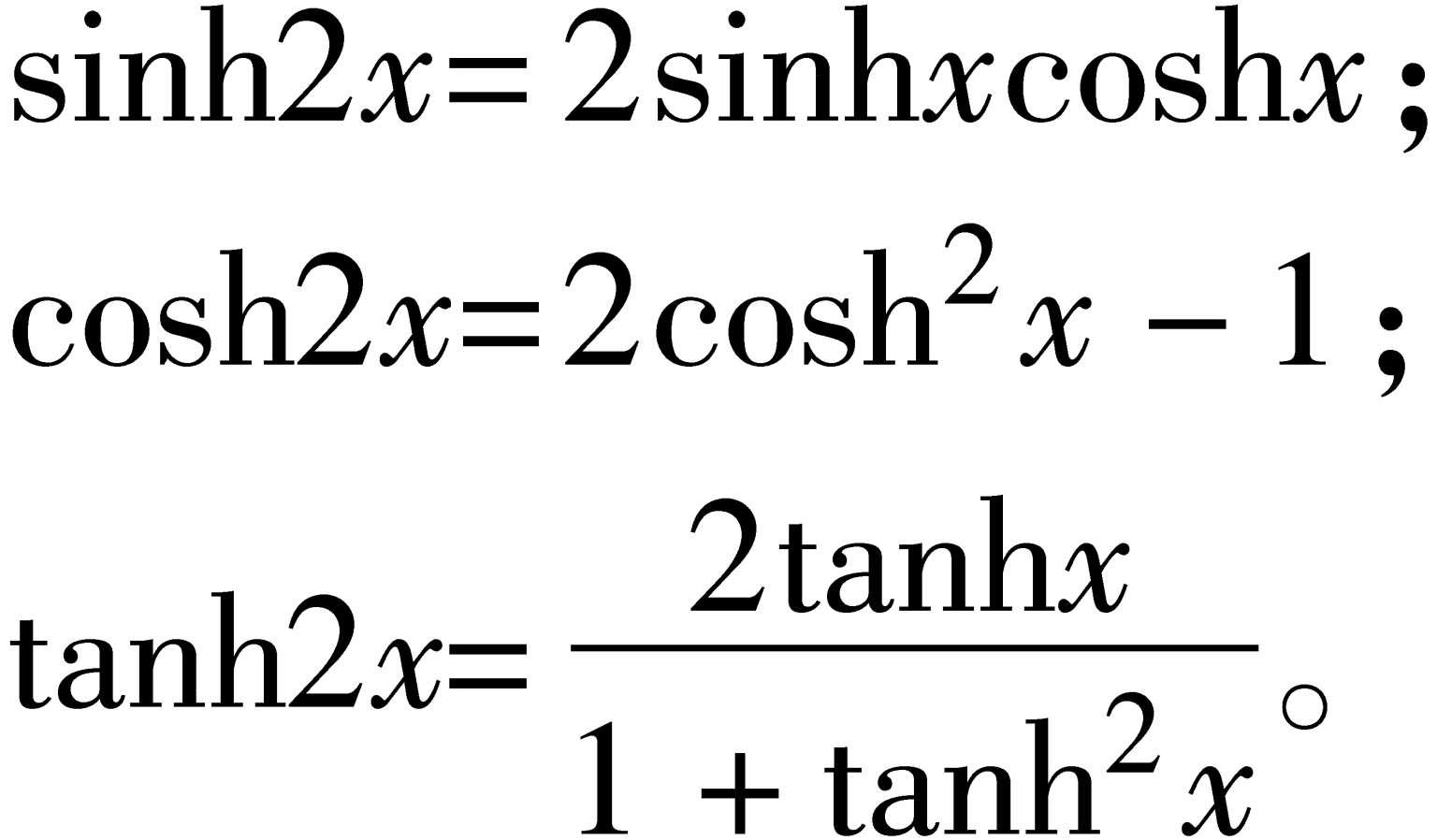
半角公式
用角x的三角函数来表示角
 的三角函数的公式。如
的三角函数的公式。如

相应地,双曲函数的半角公式有
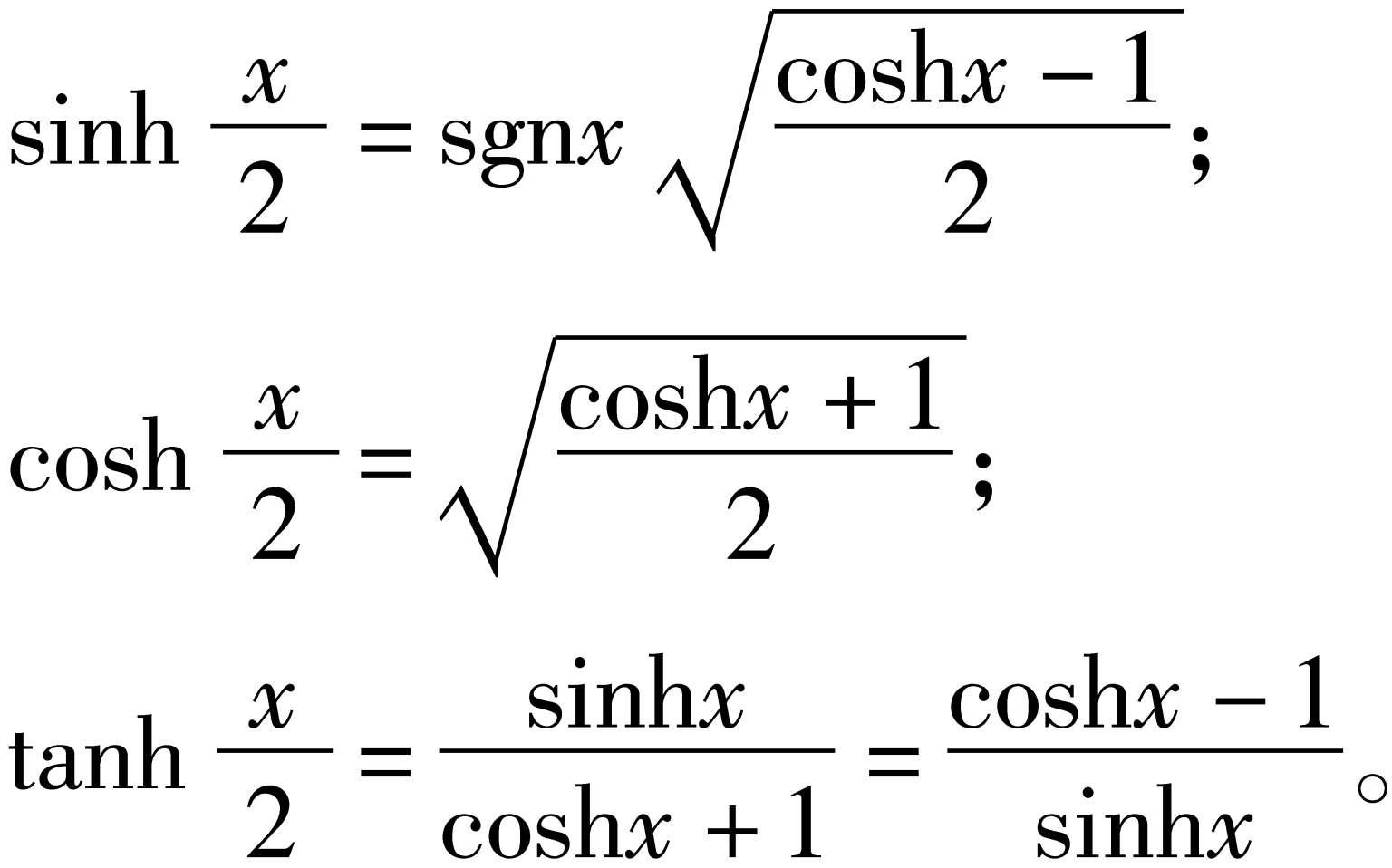
和差化积 将三角函数的和或差经过三角恒等变换,化为乘积的形式。如

积化和差 将三角函数的积经过三角恒等变换,化为和或差的形式。如
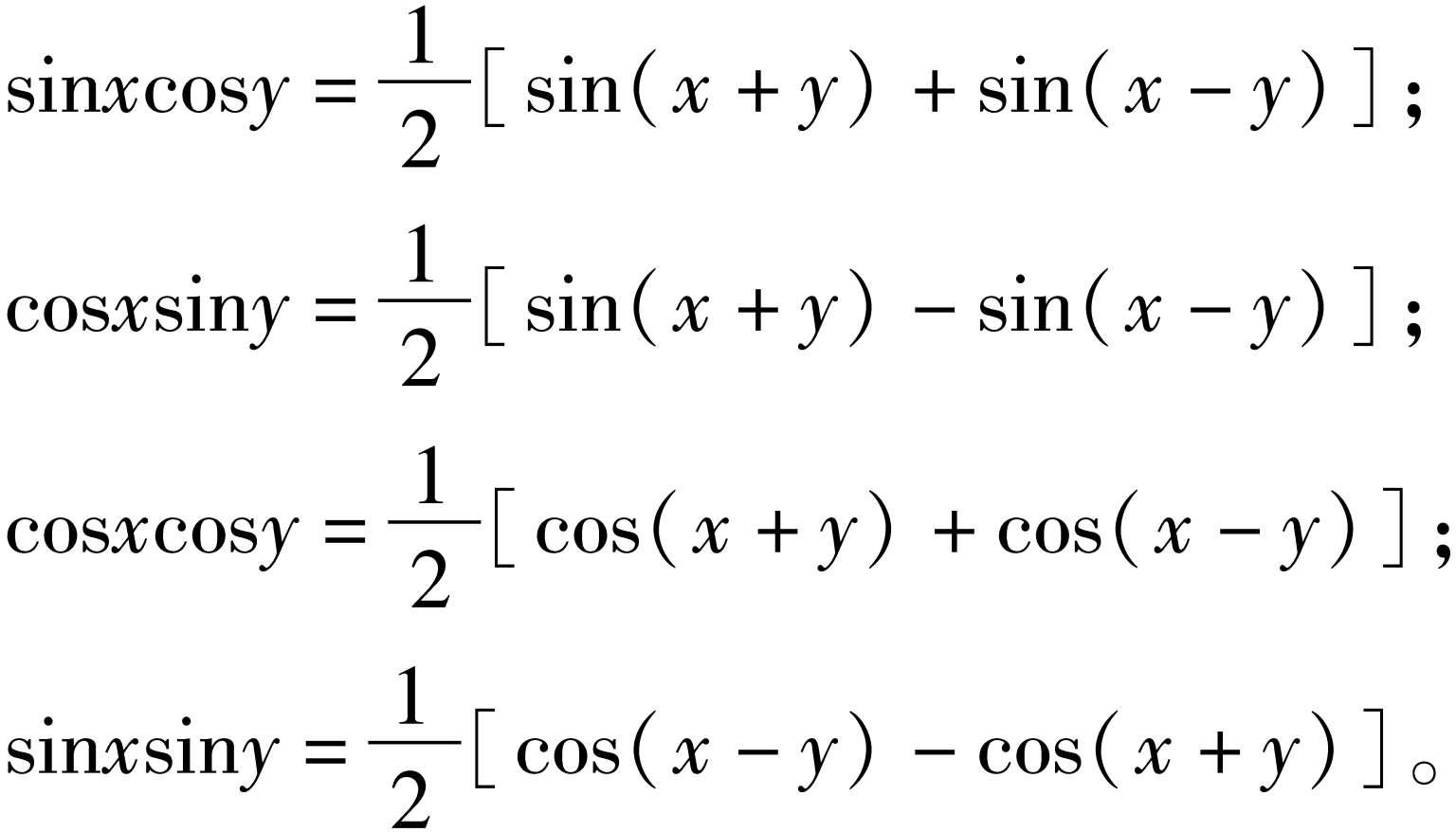
三角恒等式 在表示角的字母允许值范围内,对字母取任何数值都成立的三角函数等式。如
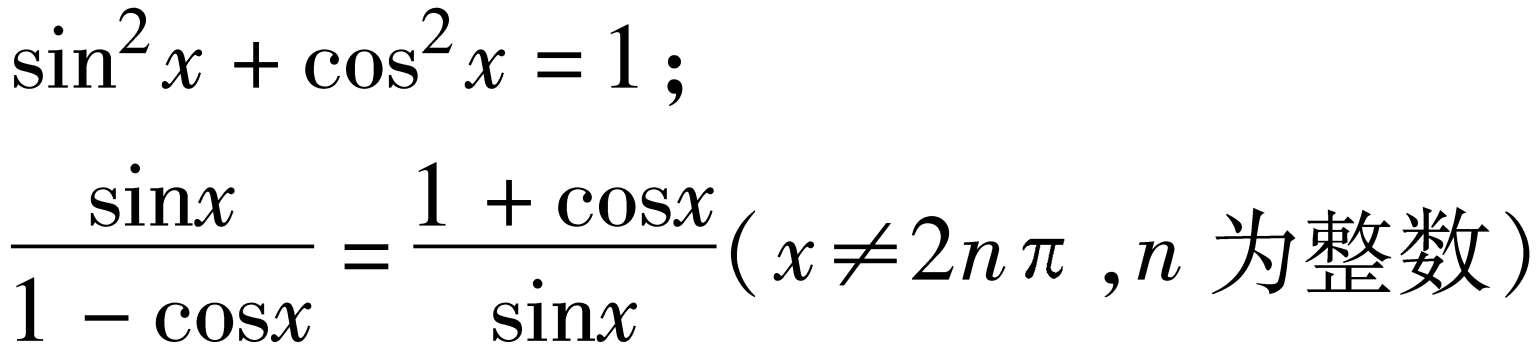
都是三角恒等式。
万能公式
角x的各种三角函数均可用tan
 来表出的一组公式。如
来表出的一组公式。如
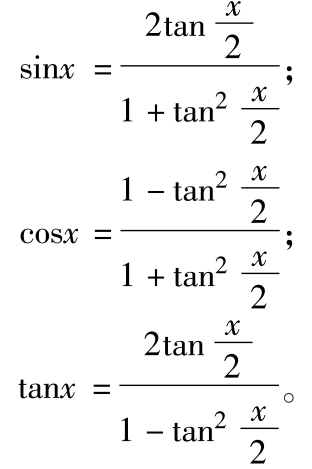
设
 ,就可以将三角函数的有理式R(sinx,cosx,…)转化为t的有理式f(t),以简化计算。
,就可以将三角函数的有理式R(sinx,cosx,…)转化为t的有理式f(t),以简化计算。
三角方程
含有未知量的三角函数的方程。例如

正弦定理 设三角形的三边为a、b、c,它们的对角分别为A、B、C,外接圆半径为R,则称关系式

为“正弦定理”。
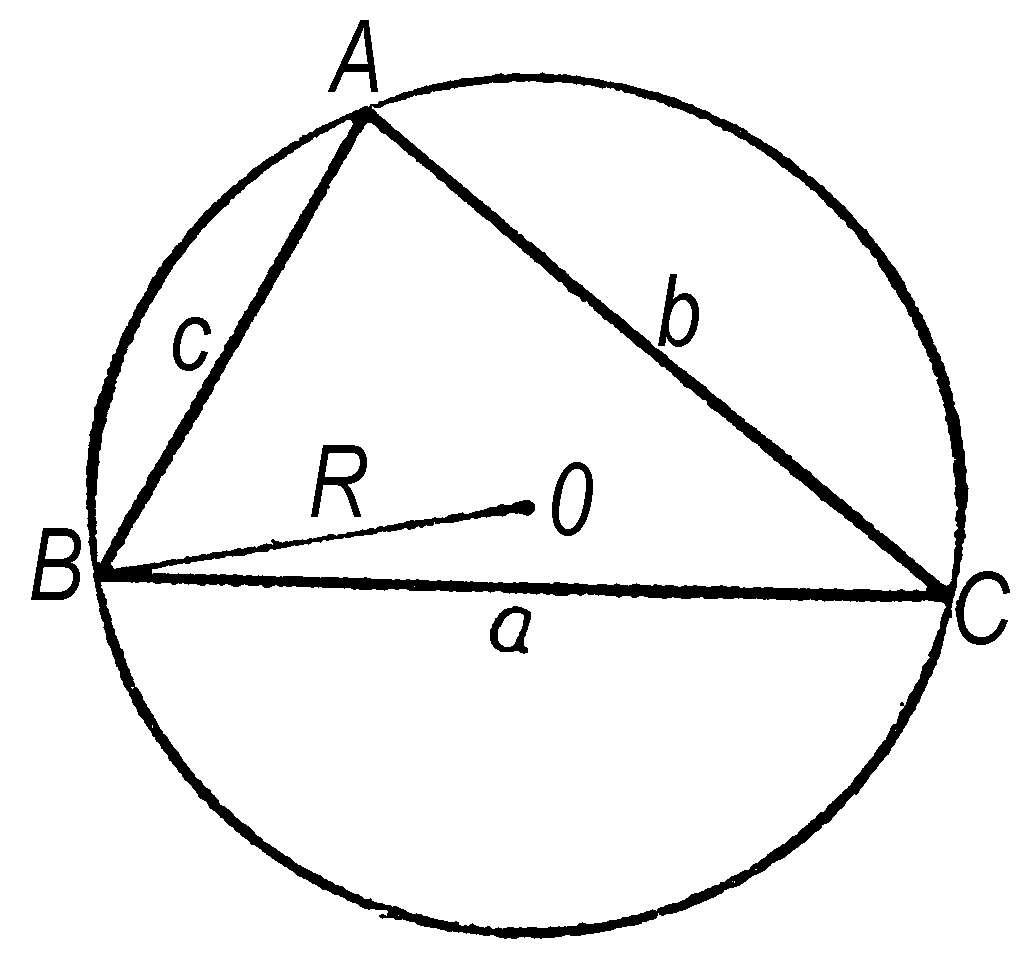
正弦定理
余弦定理 设三角形的三边为a、b、c,它们的对角分别为A、B、C,则称关系式
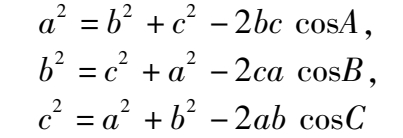
为“余弦定理”。
球面三角形
球面上由三条大圆的弧所围成的三角形。相邻两条大圆弧所成的球面角称为球面三角形的内角。球面三角形各内角之和大于
 弧度。若球半径为r,三内角分别为α
1
、α
2
、α
3
弧度,则球面三角形面积为
弧度。若球半径为r,三内角分别为α
1
、α
2
、α
3
弧度,则球面三角形面积为
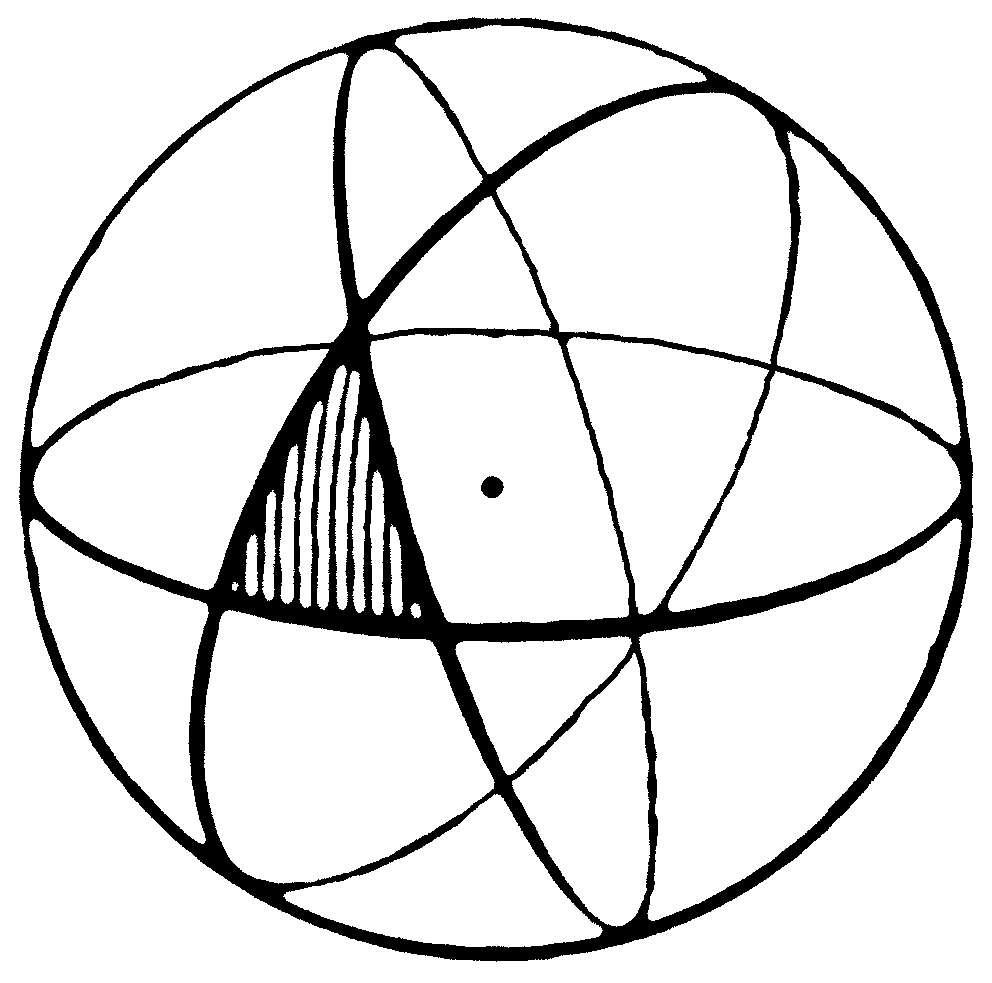
球面三角形
球面角超 亦称“球面剩余”。球面三角形三内角之和大于 180°,其间的差,称为“球面角超”,一般用E表示。球面三角形的角超与其面积成正比。
球面直角三角形 至少有一个角是直角的球面三角形。有两个直角的,称为“二直角球面三角形”。有三个直角的,称为“三直角球面三角形”,等于全球面的八分之一(如图)。
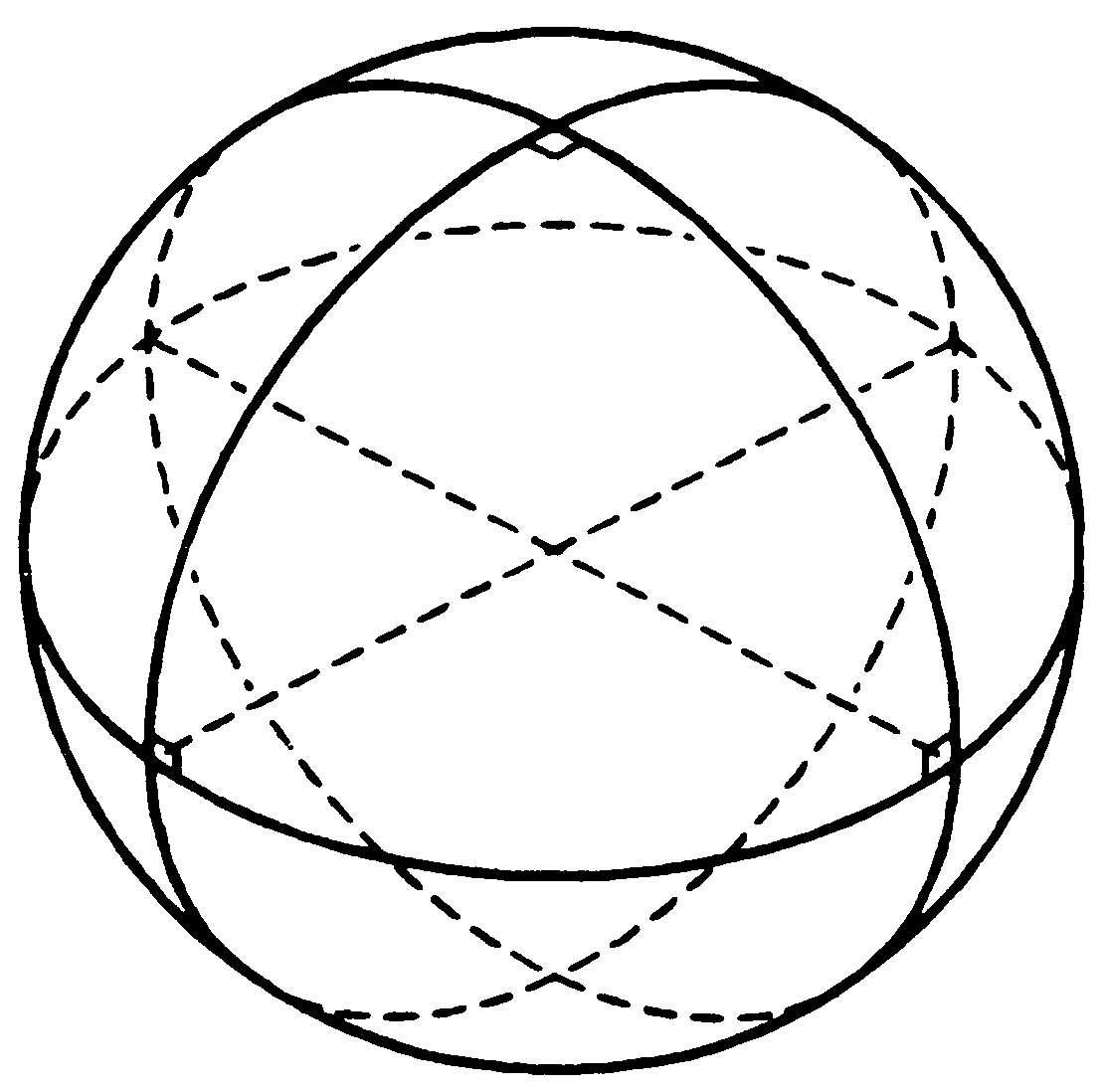
球面直角三角形


