几何·拓扑
几何学 释文见 2 页。
欧几里得几何 简称“欧氏几何”。几何学的一门分科。公元前约 300 年,古希腊数学家欧几里得总结了前人在实践中获得的几何知识,加以系统化,把公认的事实列成定义和公理,其中最著名的是平行公理:平面上一直线和两直线相交,当同旁两内角之和小于两直角时,则两直线在这一侧充分延长一定相交;即在平面上,过直线外一点只能作一条和这直线不相交的直线。用这些定义和公理来研究图形的性质,就形成了欧氏几何。按所讨论的图形在平面上或空间中,分别称为“平面几何”与“立体几何”。
平面几何 见“欧几里得几何”。
立体几何 亦称“空间几何”。见“欧几里得几何”。
球面几何 几何学的一门分科。研究球面上图形性质的几何学。是从研究天体在天球上的“视运动”发展起来的。
非欧几里得几何 简称“非欧几何”。几何学的分科。与欧几里得几何的主要区别在于改变了欧几里得的平行公理(参见“欧几里得几何”)。非欧几何有两种:双曲几何和椭圆几何。在双曲几何里,约定过一点可引两条直线与已知直线平行;在椭圆几何里,则约定没有这样的直线可引。非欧几何与欧几里得几何表面上似有矛盾,但双方都反映了现实空间的相对真理。
椭圆几何 有时亦称“黎曼几何”。见“非欧几里得几何”。
双曲几何 有时亦称“罗巴切夫斯基几何”。见“非欧几里得几何”。
解析几何 几何学的分科。如果把一个图形看成是由点所构成的,在建立了坐标系之后,则图形的几何性质可以表为这些点的坐标之间的关系,特别是代数关系。17 世纪初,法国数学家笛卡儿和费马分别利用这种关系研究几何图形,建立了解析几何。从此,变数被引进了数学,成为数学发展中的转折点,为微积分的出现创造了条件。在工程技术和物理学中,广泛利用解析几何作为研究工具。
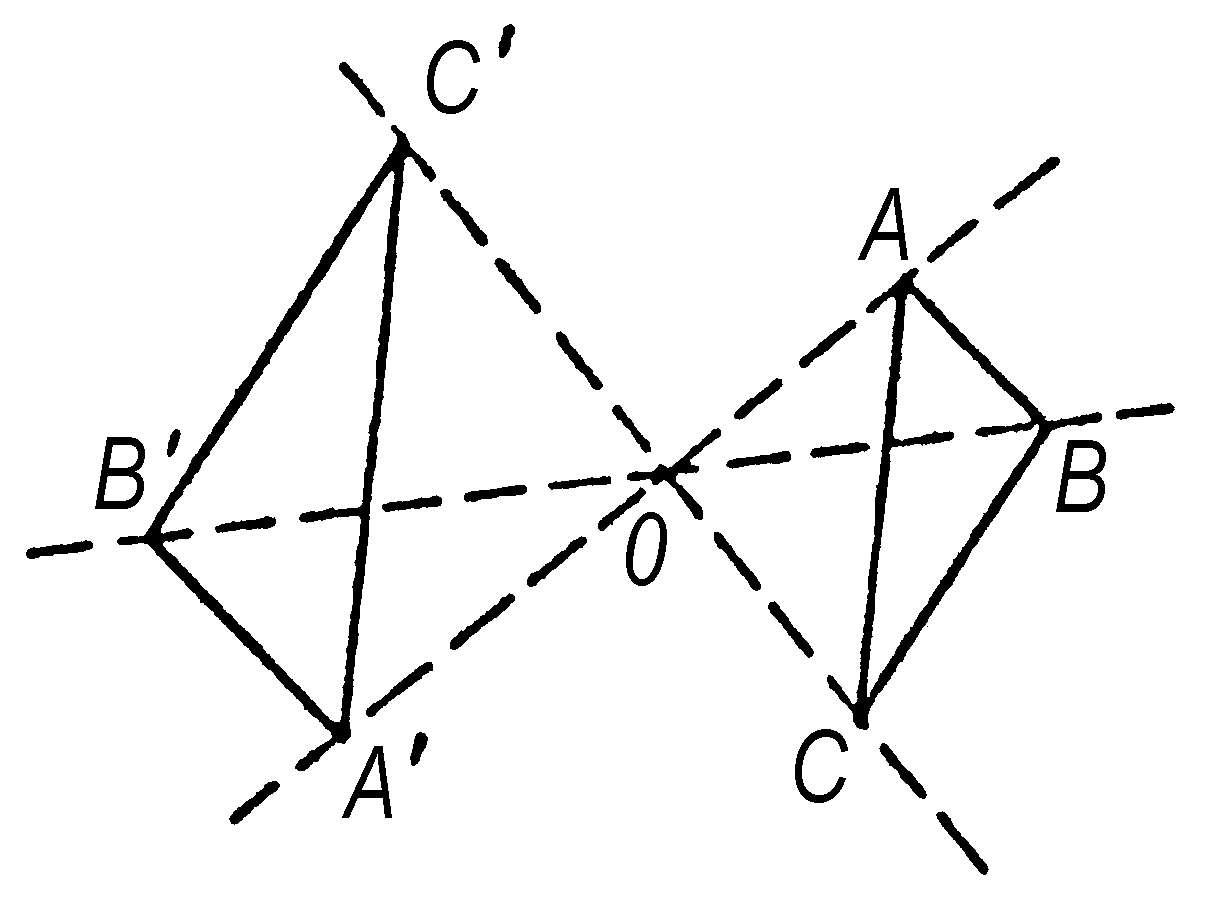
射影几何 几何学的分科。在平面上(空间中)把直线(平面)上的点经过中心投影(包括平行投影)投到另一直线(平面)上,如图中以O为投影中心,A到A′,B到B′…。所得到两直线间的对应称为“透视”。当一图形经有限次透视后变成另一图形时,称它们成“射影对应”。射影几何主要研究图形在射影对应下的不变性质。在航空、摄影和测量等方面都有应用。
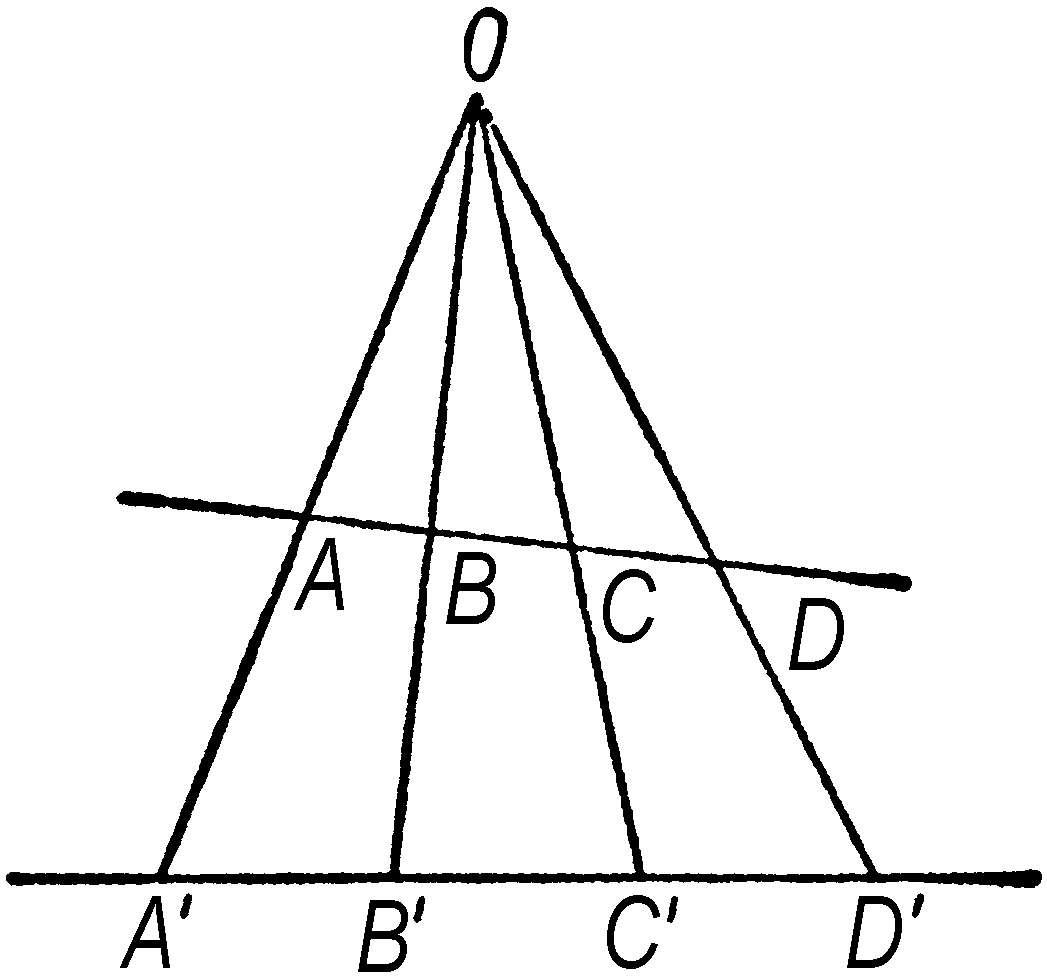
射影对应
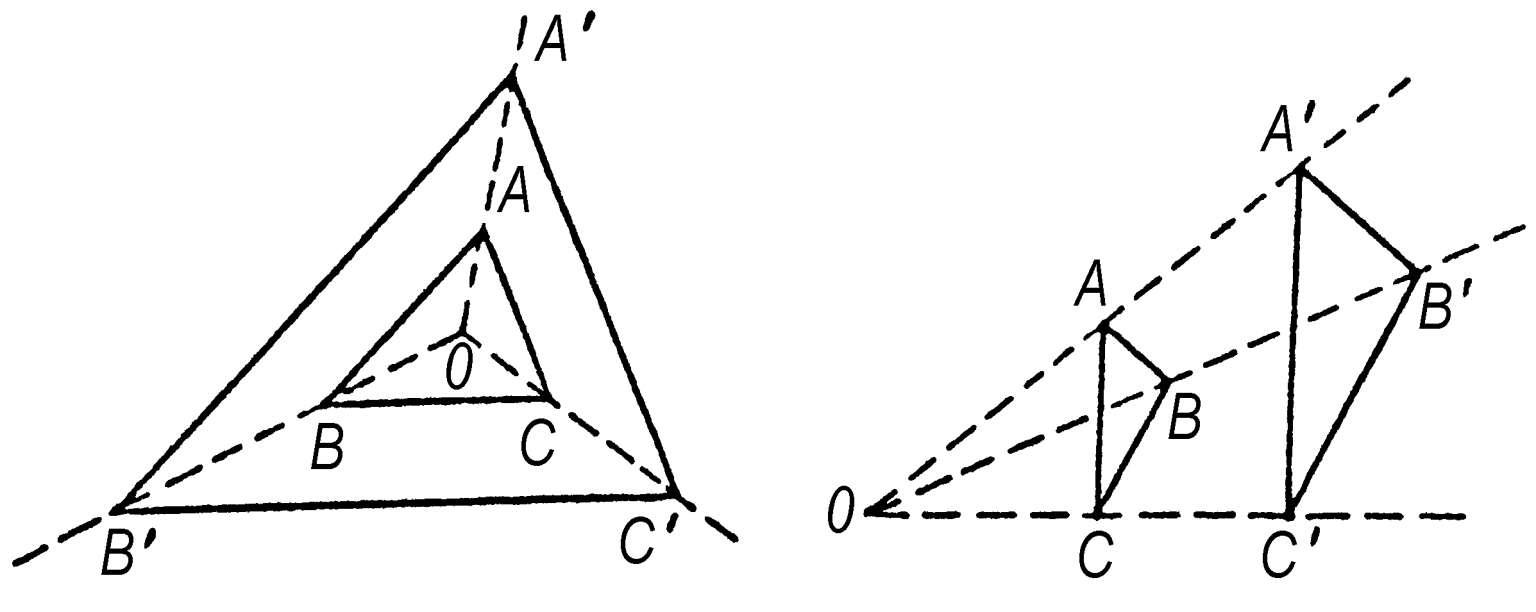
仿射几何 几何学的分科。在平面上(空间中)把直线(平面)上的点经过平行投影投到另一直线(平面)上,所得到的点与点间的对应称为“平行透视”。当一图形经有限次平行透视后变成另一图形时,称它们成“仿射对应”。仿射几何主要研究图形在仿射对应下的不变性质。
黎曼几何 几何学的分科。对n维空间中任意两个无限邻近的点都给定了距离,具体地说,点(x 1 ,…,x n )和点(x 1 +dx 1 ,…x n ,+ dx n )之间的距离可表为
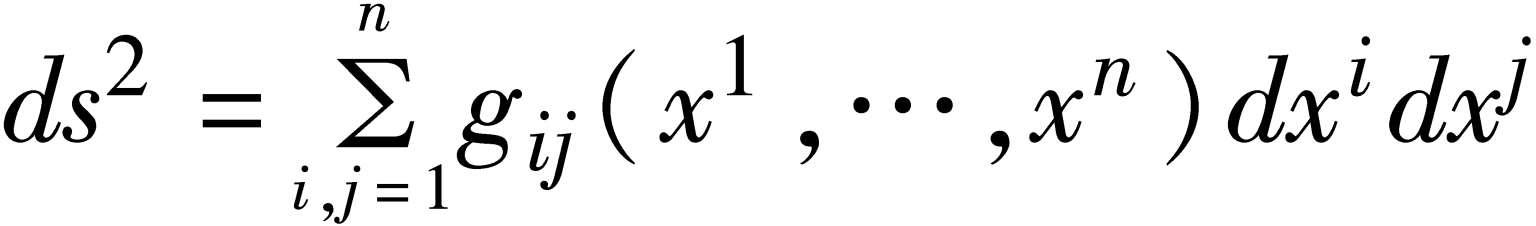
其中系数矩阵(g ij )是正定的。称ds 2 为黎曼度量,g ij 为黎曼度量张量的分量。这种空间中的每一小片都近似于欧几里得空间,但总体上却能反映出空间的弯曲的性质。1854 年黎曼首先提出了这样的几何学,后称“黎曼几何”。随着广义相对论的建立,它已成为微分几何的基础,也是微分方程、变分法、拓扑学等数学分支所需要的研究工具。20 世纪后期黎曼几何的研究主要集中在对黎曼几何的整体性质的研究,即研究黎曼几何的各种几何量(如黎曼曲率、黎奇曲率、数量曲率等)与空间的拓扑性质之间的关系。有时非欧几里得几何中的椭圆几何也被称为“黎曼几何”。
微分几何 几何学的分科。原来主要以光滑曲线、曲面为研究对象,且以数学分析、微分方程为研究工具。在力学和一些工程问题(如弹性薄壳结构、齿轮等方面)中有广泛的应用。20 世纪以来,由于力学、微分方程、理论物理、多复变函数等方面的需要,进而研究具有各种几何结构的微分流形,并着重讨论流形的整体性质和流形上的各种有重要意义的微分方程。
积分几何 几何学的分科。是从古典的几何概型问题中发展起来的。其基本问题是试图在由各种几何对象(如点、线、固定维数的仿射子空间或固定半径的球面等)所构成的集合上引入一个群不变测度(称为“运动学密度”),并用已知的几何不变量关于该运动学密度的积分去表达出各种几何上待研究的量。
代数几何 几何学的分科。以代数簇为研究对象。代数簇是由空间坐标的一个或多个代数方程所确定的点的轨迹。例如,三维空间中的代数簇就是代数曲线与代数曲面。代数几何研究一般代数曲线与代数曲面的几何性质。在复变函数论、拓扑学、微分方程论和数论中都有应用。
整体几何 几何学的分科。最初研究光滑曲线和曲面的整体几何性质。如凸闭曲线的曲率至少有四个极值点(称为“四顶点定理”);凸闭曲面是一个不能变形的曲面等等。在高维的场合,则研究光滑流形的各种整体性质。整体几何同李群、拓扑学、微分方程、多复变函数论和理论物理等学科紧密联系,互相渗透,已发展成为几何学的主流方向。
综合几何 几何学的一种。它的特点是从一些基本的几何公理出发,运用演绎推理方法,推导和论证图形的几何性质。综合几何并不建立坐标系,也不借助代数方法,而是直接研究图形的几何性质。欧几里得的平面几何和立体几何所用的就是综合几何方法。
欧几里得空间 简称“欧氏空间”。即欧几里得几何学所研究的空间。是现实空间的最简单而又相当确切的近似描述。二维和三维的欧氏空间即为通常的平面和三维空间。在现代数学中,人们也研究n维的欧几里得空间,它是由n个数所构成的数组x= (x 1 ,…,x n )的全体所得到的空间,其中两点x= (x 1 ,…,x n )和y= (y 1 ,…,y n )之间的距离定义为
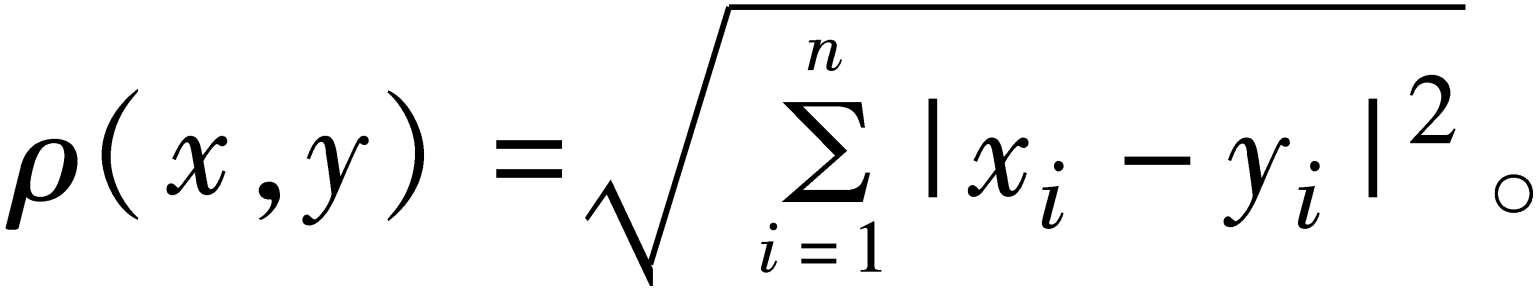
欧氏空间是研究多变量函数和线性代数的有用工具。
几何元素 构成几何图形的最基本元素点、直线、平面的总称。是人们从客观实际中,经过抽象和扩充而得到的。
公理 在一个演绎系统中不需证明而作为出发点的初始命题。如在欧几里得几何系统中,“等量加等量其和相等”、“整体大于部分”都是公理。
公理法 整理与叙述数学知识的一种常用的方法。对于数学的许多分科,人们往往把若干最根本的命题作为公理,由此再引入一些较复杂的概念并用演绎的方法推导出这分科中的其他命题。这种方法就称为公理法。公理的提出是有其实际来源或理论依据的。数学中最早的公理系统是欧几里得的几何学的公理,但并不完全。直到近代,希尔伯特提出了欧几里得几何的比较完整的公理系,为它建立了较严密的基础。在数学基础中还常讨论公理系的相容性(即公理系中诸公理的无矛盾性)、独立性和完备性。
希尔伯特公理体系 希尔伯特在 1899年出版《几何基础》一书,对欧几里得几何学的公理体系做了系统的整理,提出了严格的几何公理体系,后被称作“希尔伯特公理体系”。它采用了点、直线、平面这三个基本元素和“点在直线上”、“点在平面上”、“一点介于其他两点之间”、“两线段合同”、“两角合同”五个基本关系,以及以下五组公理:结合公理、顺序公理、合同公理、平行公理、连续公理。并且证明了:只要承认实数系统是相容的,则这套公理系统是相容的、独立的和完备的。
结合公理 有关基本元素点、直线、平面有“…在…上面”或“…通过…”等结合关系的公理。共有 8 条:(1)对于两个不同的点,恒有一直线结合其中的每个点。(2)对于两个不同的点,至多有一直线结合其中的每个点。(3)每条直线上至少有两个不同的点;至少有三个不同的点不在一条直线上。(4)对于不在一条直线上的三个点,恒有一平面通过它们中的每个点;每个平面至少有一个点。(5)对于不在一直线的三个点,至多有一平面通过它们中的每个点。(6)如果直线上的两个点在一个平面上,则此直线上的每个点都在这个平面上。(7)如果两平面有一公共点,则至少还有另外一个公共点。(8)至少有四点不在同一平面上。
顺序公理
有关基本元素点、直线、平面有“…介于…之间”介于关系的公理。共有 4 条:(1)若点B在点A和点C之间(记为A
 C),则A、B、C是一直线上的不同三点,而且B也在C和A之间。(2)对于任意两点A和B,直线AB上至少有一点C,使得B在A和C之间。(3)在一直线上的任意三个点中,至多有一点在其余两点之间。(4)亦称巴士(Pasch)公理,与一个三角形共面、但不过其顶点的直线,若与三角形的一边相交,则必与另一边相交。
C),则A、B、C是一直线上的不同三点,而且B也在C和A之间。(2)对于任意两点A和B,直线AB上至少有一点C,使得B在A和C之间。(3)在一直线上的任意三个点中,至多有一点在其余两点之间。(4)亦称巴士(Pasch)公理,与一个三角形共面、但不过其顶点的直线,若与三角形的一边相交,则必与另一边相交。
合同公理 有关图形间“…与…合同”这种合同关系的公理。共有 5 条:(1)设A、B是直线a上的两点,A′是同一或另一直线a′上的一点,则在a′上点A′的已知一侧恒有一点B′,使线段AB合同于线段A′B′,记为AB≡A′B′。(2)若两线段(可以是相同的线段)都合同于第三线段,则这两条线段也合同,即A′B′≡AB及A″B″≡AB⇒A′B′≡A″B″。(3)设开线段(AB)、(BC)均在直线a上,而且没有公共点;开线段(A′B′)、(B′C′)均在同一或另一直线a′上,亦无公共点;若AB≡A′B′,BC≡B′C′,则AC≡A′C′。(4)已知平面α上的一角∠(h,k),指定平面α′上的一直线a′的一侧,以及这条直线上以点O′为原点的一条射线h′,则α′上恰有一射线k′,使得∠(h,k)合同于∠(h′,k′),且k′在a′的已知一侧,记为∠(h,k)≡∠(h′,k′),∠(h,k)≡∠(k,h)。(5)三角形合同公理,对于两个三角形ABC和A′B′C′,若AB≡A′B′,AC≡A′ C′,∠BAC≡∠B′ A′ C′,则∠ABC≡∠A′B′C′。
连续公理 亦称“戴德金公理”。有关线段连续的公理,是任意线段能够由测量得到长度的基础。若线段AB两端及其内部的所有的点能被分为两类,具有下列性质:(i)每点恰属一类;A属于第一类,B属于第二类;(ii)第一类中异于A的每个点在A和每个第二类点之间,则必存在一点C,使得A、C间的点都属于第一类,而C、B之间的点都属于第二类。称点C为戴德金点或界点。由它所决定的分类叫作一个戴德金分割。
平行公理 刻画平行关系的公理。欧几里得平行公理(第五公设)为:在同一平面上两直线被另一直线所截,若同旁的两内角之和小于两直角,则此两直线在这一侧必定相交。而希尔伯特公理系统的平行公理为:过直线外一点,至多可引一条与该已知直线平行的直线。这两种提法是等效的。如果改变了以上的平行公理,就会得出非欧几里得几何。
平行 当平面上的两直线,或空间中的两平面,或空间中的一直线与一平面不相交时,称其间的关系为平行。
垂直 当两直线所成的角为直角时,称它们互相垂直。这个概念也可推广到两平面间或直线与平面间的情形。
正交 在几何学中,两直线互相垂直称为“正交”。如果欧氏空间中两个向量的数量积为 0,则称它们是正交的。正交的概念也可推广到更为一般的数学对象中去。
三垂线定理 立体几何中的重要定理。如果平面内的一条直线和这个平面的一条斜线在该平面内的正射影垂直,则它也和这条斜线垂直。上述定理的逆命题也成立。
距离 几何学的基本概念之一。对不同对象有不同的规定。例如,在欧几里得空间中,两点间的距离是连接这两点的直线段的长。从一点到一直线或一平面的距离是从这点向直线或平面所引的垂线段的长;两平行线或平行面的距离是指它们间公共垂线段的长。在球面上,两点的距离是由这两点所确定的大圆的劣弧的长。距离的概念也可推广到更为一般的数学对象中去。
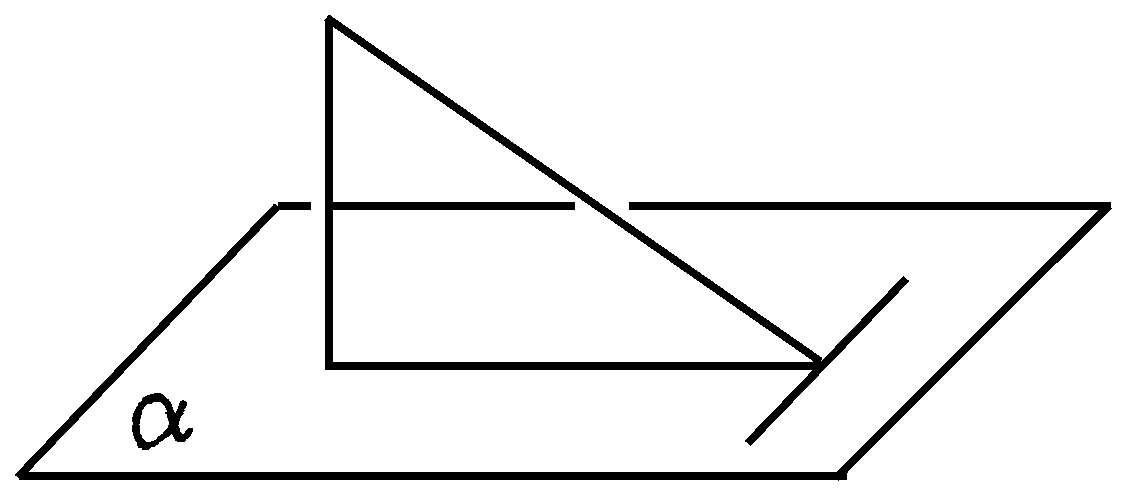
三垂线定理
面积 几何学的基本度量之一。是用以度量平面或曲面上一块区域大小的正数。通常以边长为单位长的正方形的面积为度量单位。例如,两边长为a米和b米的矩形的面积等于ab平方米。
体积 几何学的基本度量之一。是用以度量空间区域大小的正数。通常以边长为单位长的立方体的体积为度量单位。例如,三边长为a米、b米、c米的长方体的体积等于abc立方米。
容积 器皿容纳物质的体积称为该器皿的“容积”。
轨迹 在给定的条件下,动点所描出的图形。或者说是满足一定条件的点的全体所成的集合。例如,平面上离定点有定距离的动点的轨迹是圆。
直线 几何基本元素之一。一点在平面上或空间中沿一定方向和其相反方向运动,所成的轨迹是直线,它可向两个方向无限伸展。通过两点只能引一条直线。两点间以直线距离为最短。
射线 从一个定点出发沿一个定方向运动的点的轨迹。
线段 从直线上截下的有限的一段。
折线 把不在一直线上的若干点用线段逐点连接起来的图形。第一点是起点,最后一点是终点,其他各点称为“顶点”,各线段称为“边”。当起点和终点重合时,称为“封闭折线”。
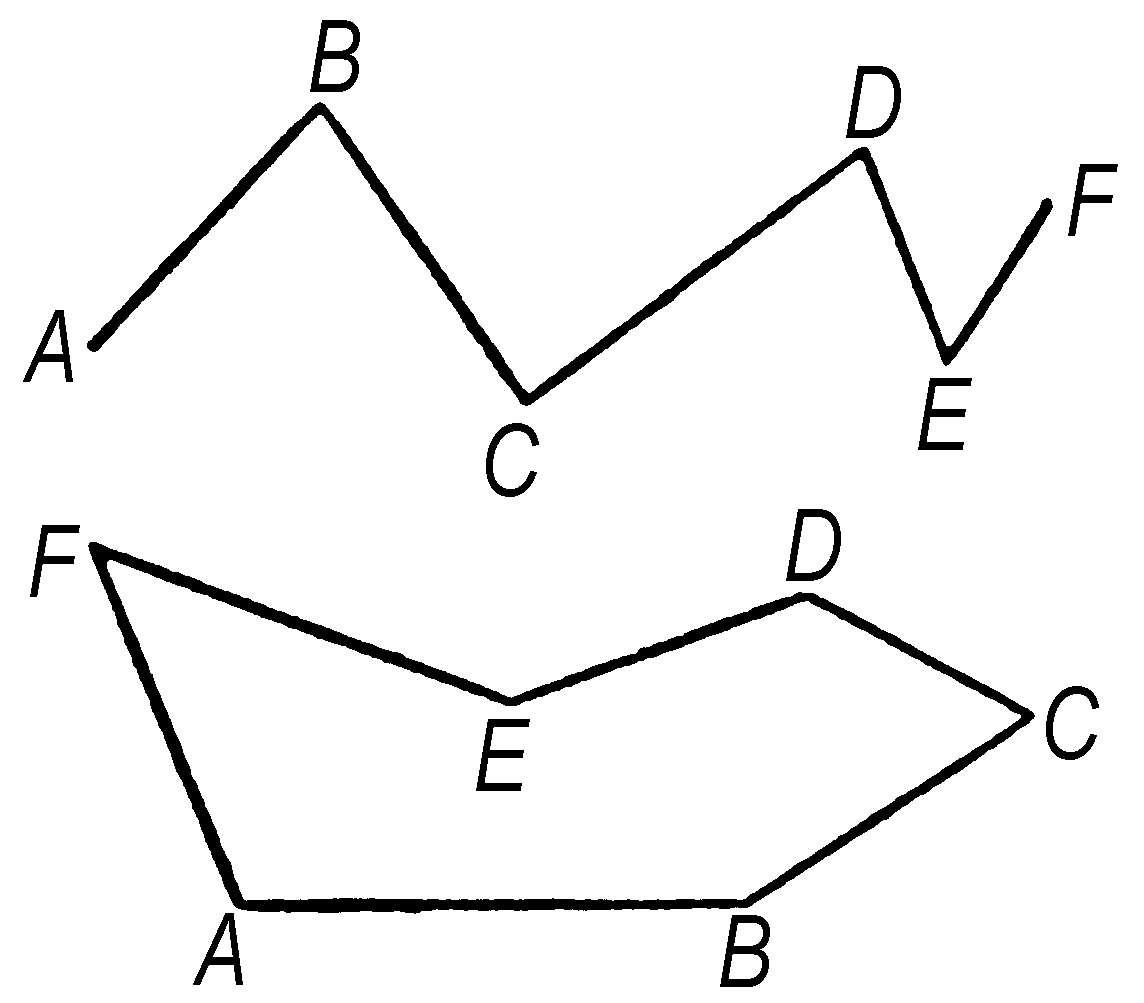
折 线
公度 对于线段a和b,如果存在线段d,使a、b都恰好是d的整数倍,则称线段d为线段a和b的“公度”;否则称线段a和b“无公度”。无公度的线段是存在的,例如,正方形的边和对角线就是无公度的。人们最初就是通过无公度的线段发现了无理数。
平面 把水平面抽象化了的几何元素。平面的基本性质有:(1)若一条直线上的两点在一个平面内,则该直线上所有的点都在这平面内;(2)若两个平面有一公共点,则它们相交于过这个点的一条直线;(3)过不在同一直线上的三点,有且只有一个平面。
截面 “几何截面”的简称。工程上称为“剖面”。用一个平面和物体相交所得的平面图形。在不同位置相交时,所得截面的形状一般不相同。
角 由一点发出的两条射线所夹成的平面图形。这点称为角的顶点,射线称为角的边。当构成角的两边的射线方向相反时,所夹的角称“平角”。平角的一半称“直角”。平角的两倍称“周角”。小于一个直角的角称“锐角”,大于一个直角而小于一个平角的角称“钝角”。角也可以看成是由一条射线绕着它的端点,从起始位置顺着指定的方向转到终止的位置而形成的。习惯上,把射线绕逆时针向旋转生成的角,称为“正角”;按顺时针向旋转生成的角,称为“负角”。
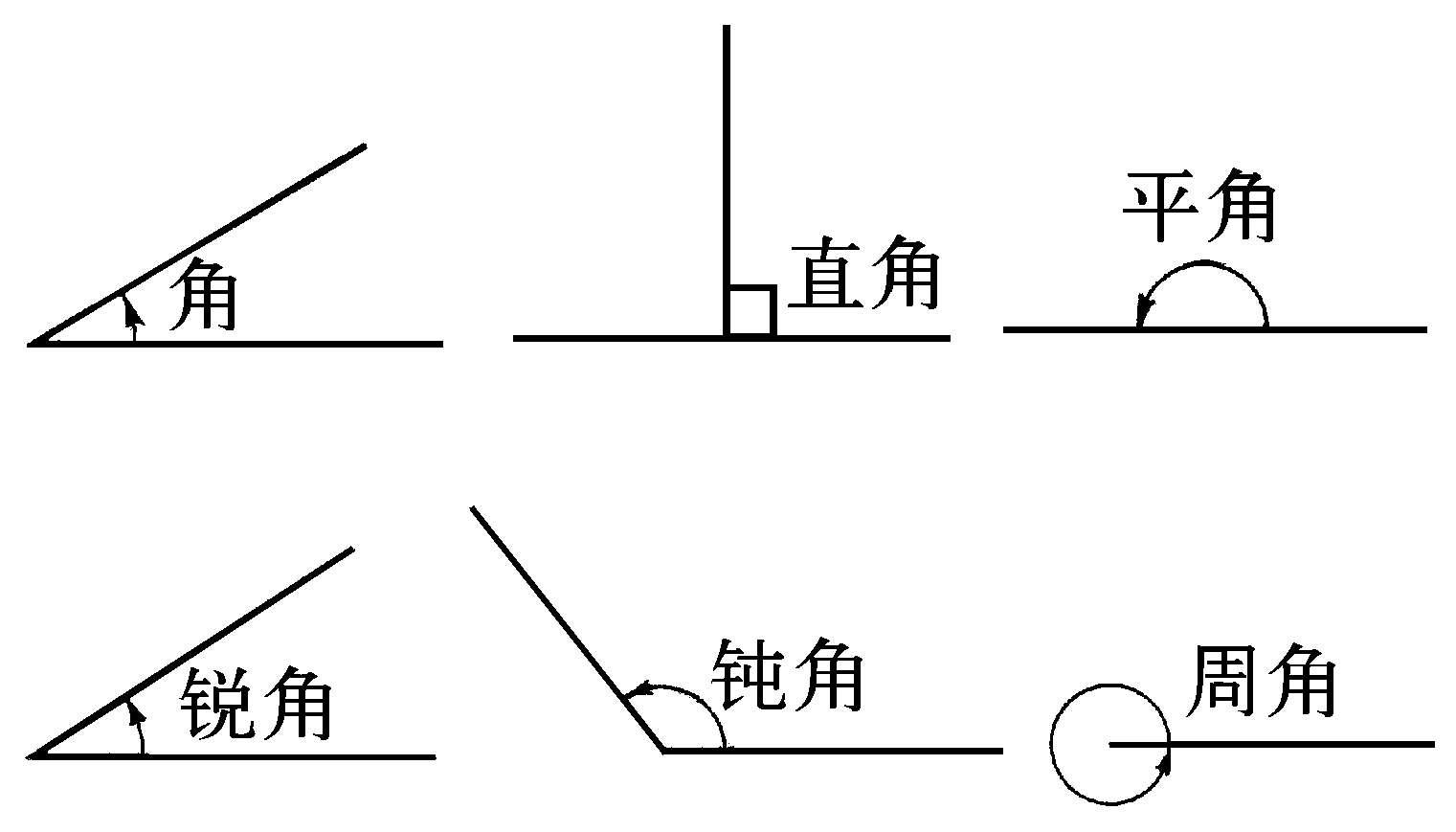
角
平角 见“角”。
直角 见“角”。
周角 见“角”。
锐角 见“角”。
钝角 见“角”。
余角 两角的和等于一直角时,每一角称为另一角的“余角”。例如,直角三角形两锐角互为余角。
补角 两角的和等于两直角时,每一角称为另一角的“补角”。例如,三角形的每个内角和它的外角互为补角。
邻角 如果平面上两角有公共顶点和一公共边,且其他二边分别在公共边的两旁,则称每一角为另一角的“邻角”。
对顶角 把一角的两边分别向相反方向引延长线,两延长线所夹的角称为原角的“对顶角”。两对顶角大小相等。
三线八角 平面上一直线和两直线相截所得的八个角的统称。八个角依其相互位置给以不同的名称。∠1 与∠2,∠3 与∠4 相互交错,且均在外方,称为“外错角”。∠5 与∠6,∠7与∠8 相互交错,且均在内方,称为“内错角”。∠1 与∠4,∠2 与∠3 在截线的同旁,且均在外方,称为“同旁外角”。∠5 与∠8,∠6 与∠7 在截线的同旁,且均在内方,称为“同旁内角”。∠2 与∠5,∠3 与∠8,∠4 与∠7,∠1 与∠6 位置分别相同,称为“同位角”。
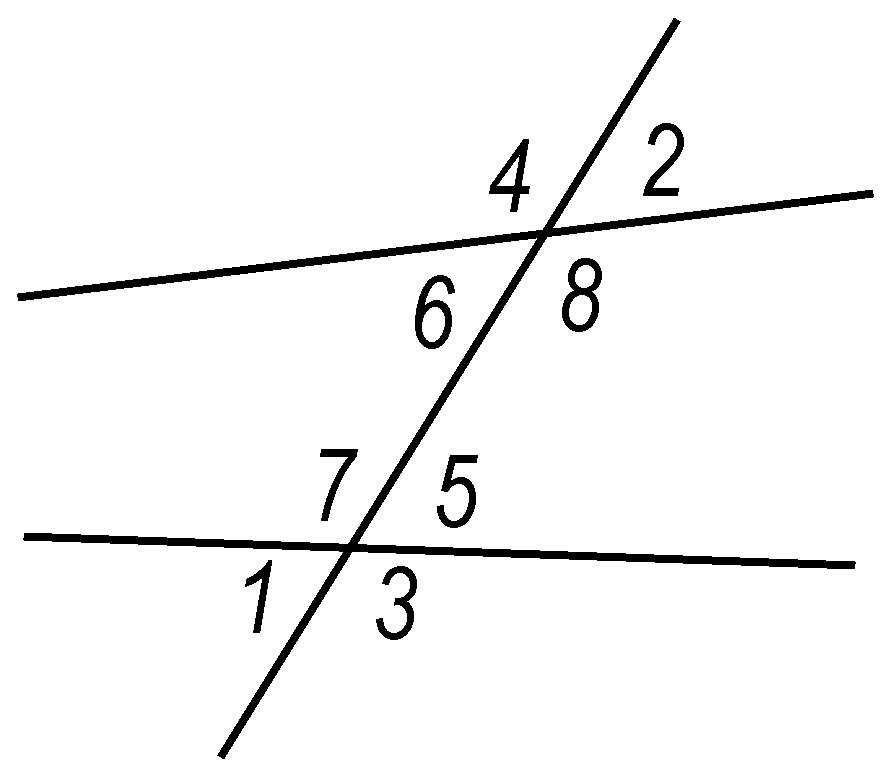
三线八角
外错角 见“三线八角”。
内错角 见“三线八角”。
同旁外角 见“三线八角”。
同旁内角 见“三线八角”。
同位角 见“三线八角”。
三角形 把不在一直线上的三点,两两用线段连接起来的图形。各点称为“顶点”,连接两顶点的线段称为“边”,每两边所夹的角称为“内角”。在欧几里得几何中三角形三个内角之和等于两直角。三角形的三内角都是锐角的,称为“锐角三角形”;有一个内角是直角的,称为“直角三角形”;有一个内角是钝角的,称为“钝角三角形”;两边相等的三角形称为“等腰三角形”;三边相等的称为“正三角形”或“等边三角形”。从三角形一顶点向对边或其延长线所引垂线的线段,称为以该对边为底边的三角形的“高”;垂线段的长也称为高。三角形的面积等于底边的长与高的乘积的一半。
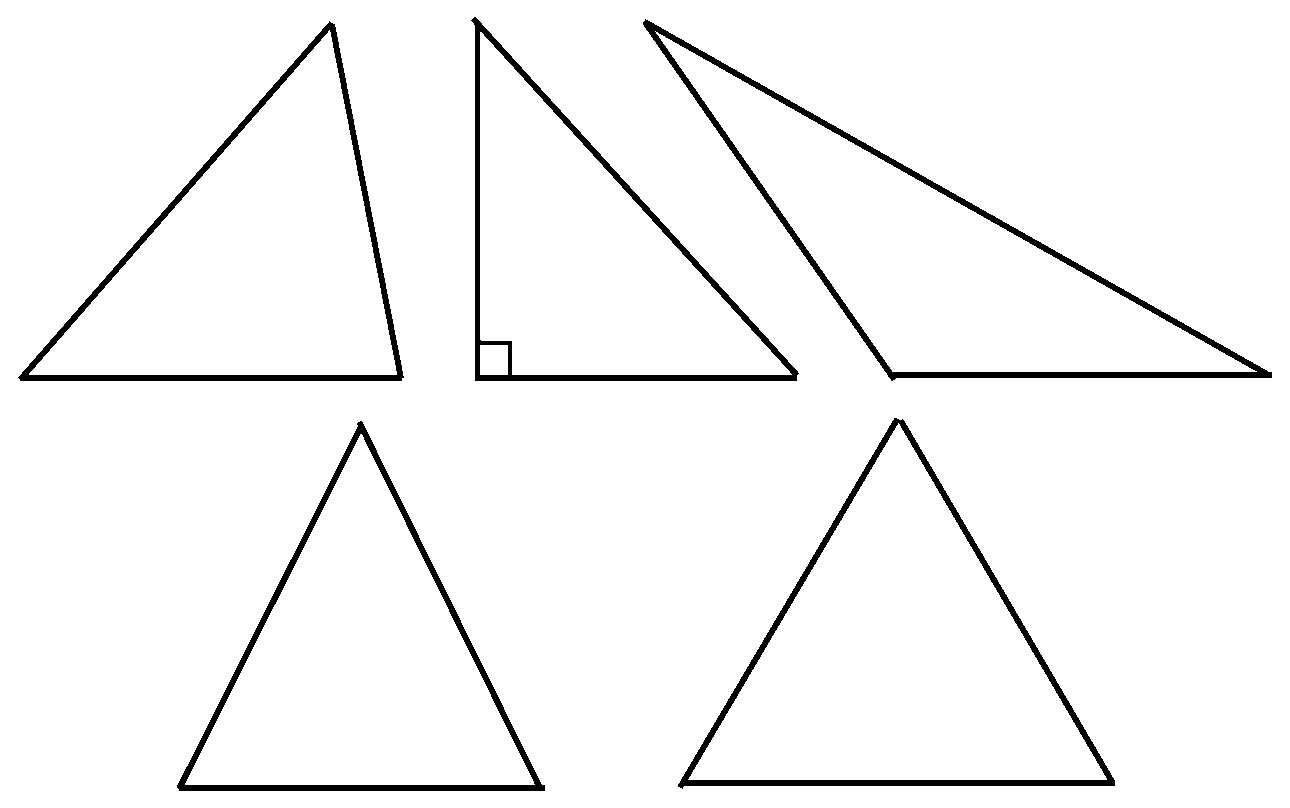
三角形
锐角三角形 见“三角形”。
直角三角形 见“三角形”。
钝角三角形 见“三角形”。
等腰三角形 两边相等的三角形。
正三角形 三边相等的三角形。
中线 三角形顶点与其对边中点的连线。
垂线 设两条直线垂直相交,则称其中一条为另一条的垂线。与一定平面垂直的直线则称为平面的垂线。交点都称为垂线的垂足。
垂足 见“垂线”。
斜线 设两条直线相交而不互相垂直,则称其中一条为另一条的斜线。与一定平面斜交的直线则称为平面的斜线。其交点都称为“斜线足”,简称“斜足”。
中垂线 线段的垂直平分线。即过线段的中点且垂直于该线段的直线。
垂心 三角形的三条高或其延长线相交于一点,这点称为三角形的垂心。
重心 三角形的三条中线相交于一点,这点称为三角形的重心。重心和三角形顶点的连线长度等于所在中线长度的三分之二。
内心 三角形内切圆的圆心。是三角形三个内角的平分线的交点。
外心 三角形外接圆的圆心。是三角形三条边的垂直平分线的交点。
旁心 三角形旁切圆(与三角形的一边和其他两边的延长线相切的圆)的圆心。是三角形一个内角的平分线与另两个角的外角平分线的交点。
欧拉线 三角形的垂心、外心和重心在一条直线上,这条直线称为三角形的“欧拉线”。并且垂心到重心的距离等于外心到重心的距离的两倍。如图,△ABC中,H为垂心,O为外心,G为重心,则H、G、O三点共线,且HG = 2GO。
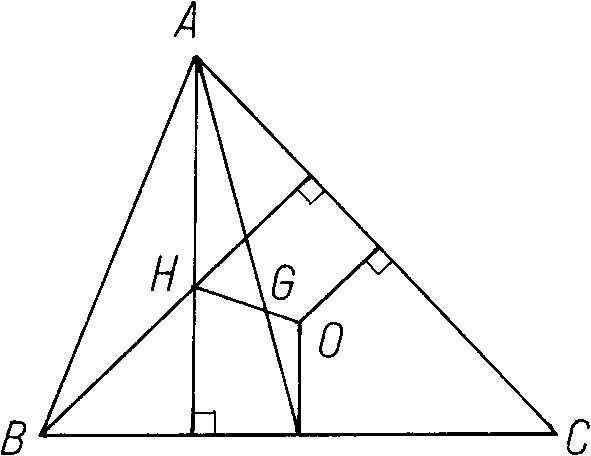
欧拉线
中位线 连接三角形任意两边中点的线段,称为此三角形的“中位线”。一个三角形有三条中位线,三角形的中位线平行于第三边,且等于第三边的一半。连接梯形两腰中点的线段,称为此梯形的中位线。它平行于梯形的两底,且等于两底和的一半。
勾股定理 亦作“句股定理”。西方称“毕达哥拉斯定理”。直角三角形斜边上的正方形面积等于两直角边上的正方形面积之和。中国古代称两直角边为勾和股,斜边为弦,在《周髀算经》所载的商高答周公问中,曾提出“勾广三,股脩四,径隅五”的关系。
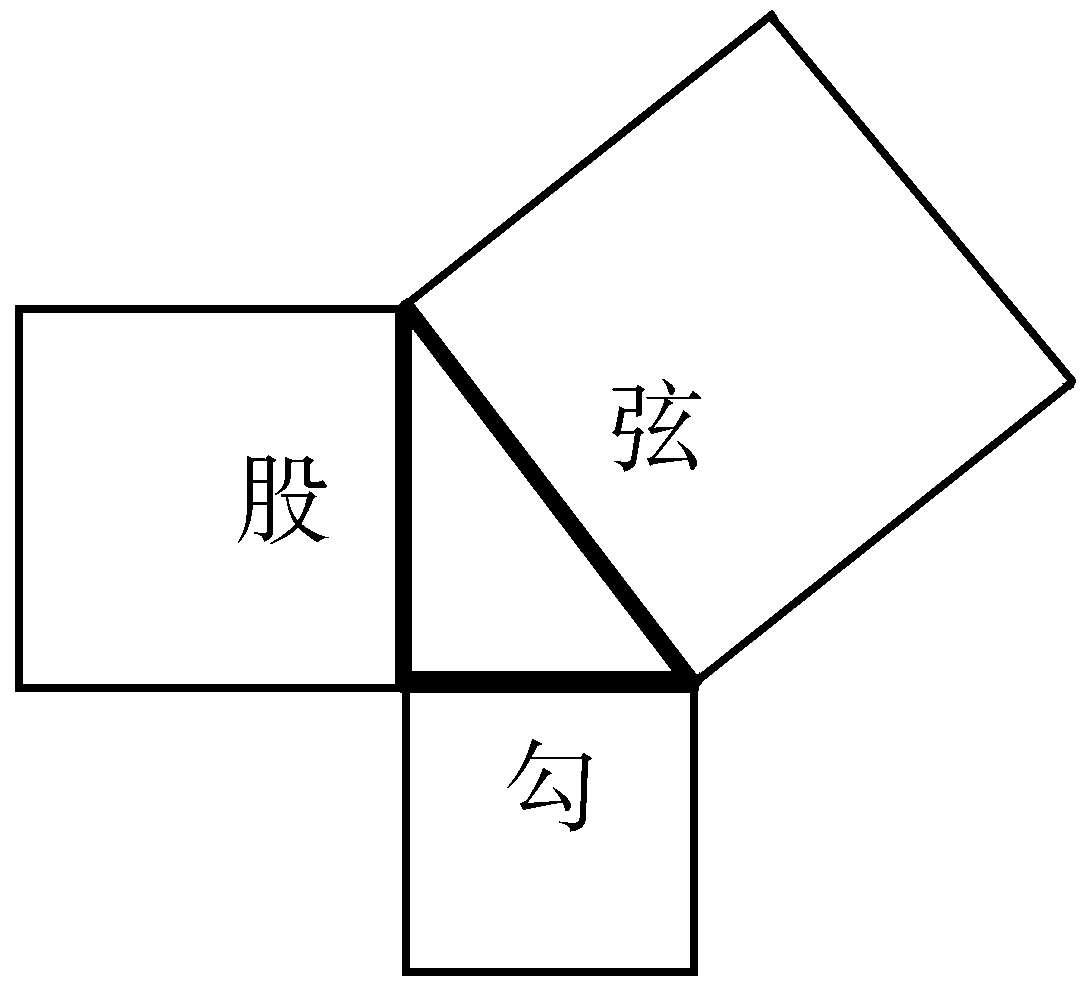
勾股定理
海伦公式 指求三角形面积的下述公式:
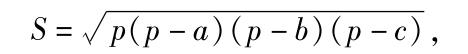
其中a、b、c为三角形的三边长,p为三角形的半周长。希腊学者海伦在他的著作《度量论》中证明了这一公式,故名。其实,古希腊的阿基米得就已知道这一公式;中国数学家秦九韶在《数书九章》中记述的三斜求积公式也和它一致。
凸图形 一种特殊的图形。这种图形中任意两点间的连接线段全部位于此图形之中。
多边形
亦称“多角形”。平面上封闭折线所构成的图形。折线的顶点和边分别称为多边形的顶点和边。连接不相邻两顶点的线段称为多边形的“对角线”。边数与顶点数相等,且至少等于 3。除顶点外,如各边彼此不相交,则称为“简单多边形”。若一简单多边形所有的内角都不超过
 ,称为“凸多边形”;否则,称为“凹多边形”。内角相等的等边多边形称为“正多边形”。
,称为“凸多边形”;否则,称为“凹多边形”。内角相等的等边多边形称为“正多边形”。
凸多边形
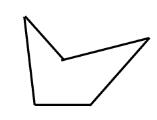
凹多边形
凸多边形 见“多边形”。
凹多边形 见“多边形”。
正多边形 见“多边形”。
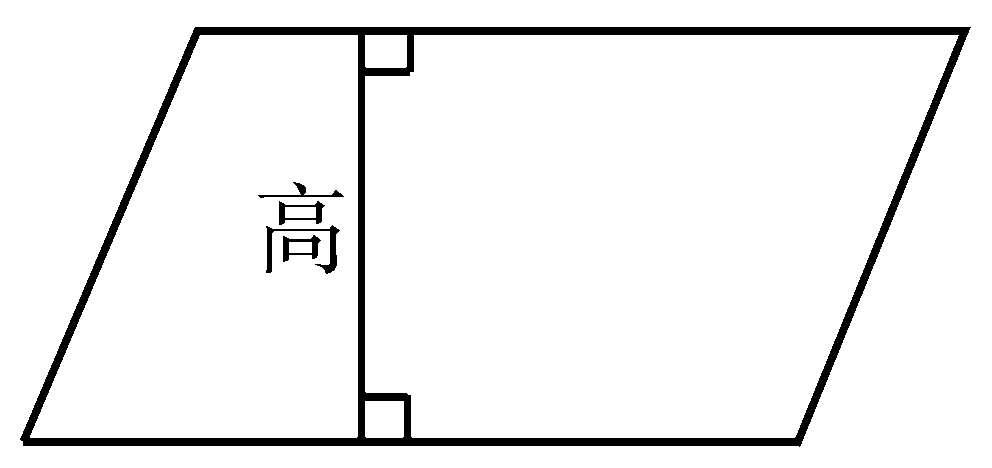
平行四边形 对边互相平行的四边形。它的对角线互相平分,对边相等,对角相等。把平行四边形的一边作为底边,底边与对边间的公共垂线的线段和它的长度都称为高。平行四边形的面积等于底边长与高的乘积。它是中心对称图形,对角线的交点是其对称中心。
平行四边形
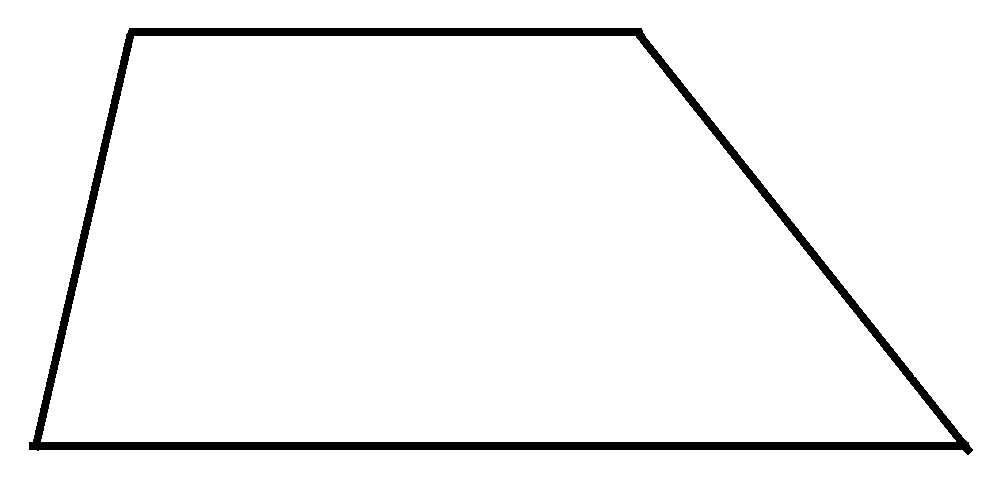
梯形 一双对边平行而另一双对边不平行的四边形。平行的对边称为梯形的“底边”,另一双对边称为“腰”。两腰相等的称为“等腰梯形”。两底边间公共垂线的线段和它的长度都称为梯形的高。梯形的面积等于两底边长的和与高的乘积的一半。
梯 形
矩形 通称“长方形”。是平面上每个内角都是直角的四边形。它的对角线相等且互相平分。面积等于相邻两边长的乘积。矩形是中心对称图形,又是轴对称图形,两条对边中点的连线是其对称轴。
长方形 即“矩形”。
菱形 平面上四边相等的四边形。它的对角线互相垂直平分。面积等于两对角线长度的乘积的一半。菱形是轴对称图形,两条对角线是其对称轴。
正方形 四边相等的矩形。它具有平行四边形、矩形和菱形的所有特性。既是中心对称图形,又是轴对称图形。面积等于边长的平方。
多边形的角
平面上简单多边形的相邻两边在形内所夹的角,称为多边形的“内角”。多边形一边与其一邻边的延长线所夹的角,称为多边形的“外角”。简单n边形共有n个内角。n个内角的和等于(n-2)
 。
。
内角 见“多边形的角”。
外角 见“多边形的角”。
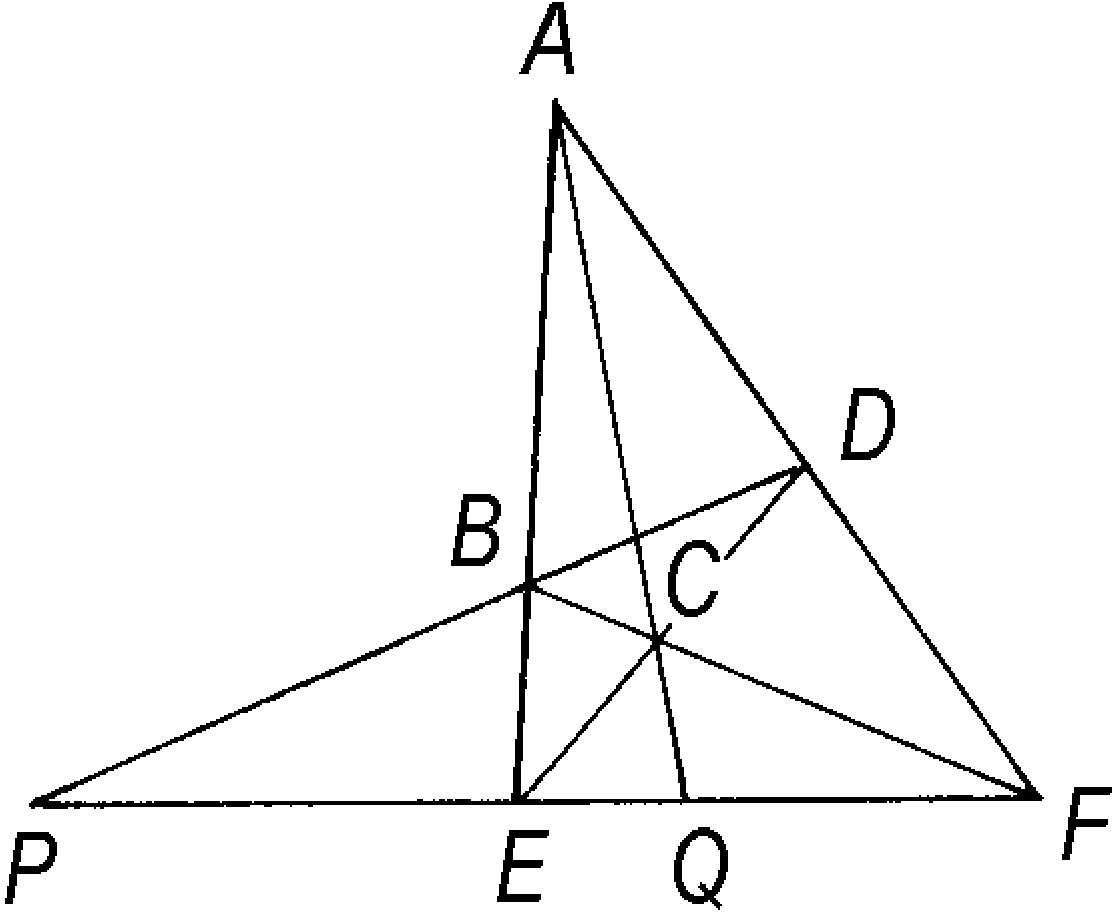
完全四边形 四条直线两两相交,共有六个交点,这四线六点所形成的图形称为“完全四边形”(如图)。四条直线称为它的边,六个交点称为它的顶点。不共边的两个顶点称为对顶点,它们的连线称为对角线。设对角线BD、AC分别交EF于P、Q,则P、Q调和分割线段EF。
完全四边形
相似形 形状相同,大小不一定相等的图形。以多边形为例,如果两个多边形的对应边成比例而且对应角相等,则称这两个多边形是相似多边形。
圆内接多边形 顺次连接圆周上若干个点所成的多边形。称这圆为多边形的“外接圆”。
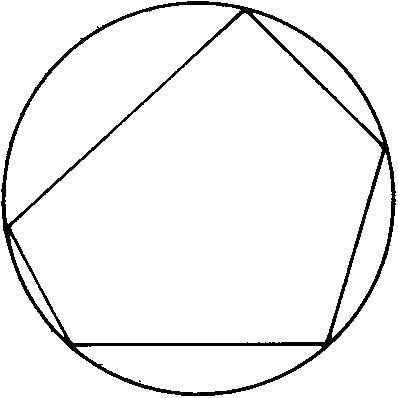
圆内接多边形
圆外切多边形 各边都和同一圆相切的多边形。称这圆为多边形的“内切圆”。
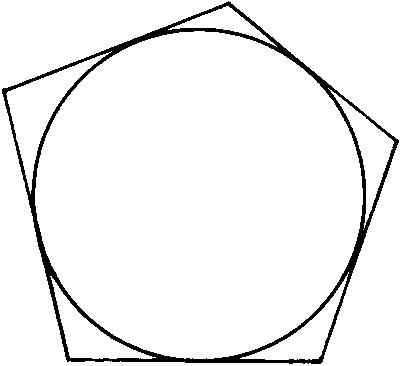
圆外切多边形
外接圆 见“圆内接多边形”(89 页)。
内切圆 见“圆外切多边形”(89 页)。
圆
在平面上,和定点有定距离的动点的轨迹。定点称为“圆心”,定距离称为圆的“半径”。有时也称轨迹所围的部分为“圆”,而称轨迹为“圆周”,称连结圆心与圆周上一点的线段为“半径”。圆周的一部分称为“圆弧”,小于半圆周的圆弧称为“劣弧”,大于半圆周的称为“优弧”。连接圆周上两点的直线段称为“弦”,过圆心的弦称为圆的“直径”,直径长为半径的两倍。半径为r的圆的周长为 2
 r,面积等于
r,面积等于
 r
2
,
r
2
,
 是圆周率。
是圆周率。
圆周 见“圆”。
半径 见“圆”。
弦 见“圆”。
圆弧 见“圆”。
圆心角 连接圆心和圆弧两端点的线段(半径)对这圆弧所张的角。圆心角的度数等于它所对的弧的度数。
圆周角 连接圆周上一点到圆弧两端点的弦对这圆弧所张的角。圆周角的度数等于它所对弧的度数的一半。
弦切角 圆的切线与过切点的弦所夹的角。弦切角的度数等于它的两边所夹的弧的度数的一半,也等于此弧上的圆周角。如图,弦切角∠ABC等于圆周角∠ADB。
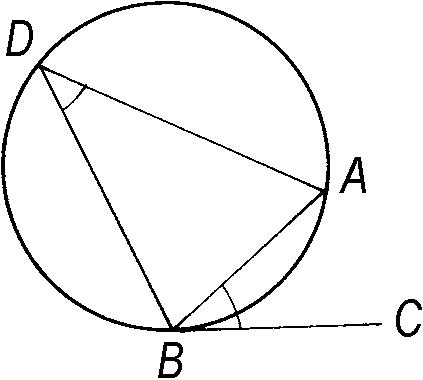
弦切角
圆周率
中国古代称“圆率”、“周率”或“圆的周径相与之率”。圆周的长同它直径的比值。是一个常数,用希腊字母
 表示:
表示:
它是一个无理数,又是超越数。中国南北朝祖冲之计算
 的近似值,得到
的近似值,得到
 的“约率”22 /7,“密率”355 /113。
的“约率”22 /7,“密率”355 /113。
圆面积
半径为r的圆的面积等于
 r
2
,
r
2
,
 是圆周率。
是圆周率。
圆幂定理 过已知圆O所在平面上任一点S作直线,如果此直线和圆O相交于点A、B,则SA·SB为一常数,且等于OS 2 -R 2 (R为圆O的半径)。称这常数值为点S关于圆O的幂,简称“圆幂”。上述命题即称“圆幂定理”。
扇形 圆的两半径所夹的部分。面积等于它所对的弧长和圆半径乘积的一半。
弓形 一段圆弧与其所对弦围成的图形。当圆弧为劣弧时,称为“劣弓形”;当圆弧为优弧时,称为“优弓形”(参见“圆”)。如果l、h、k分别是弓形的弧长、高和底,则弓形的面积
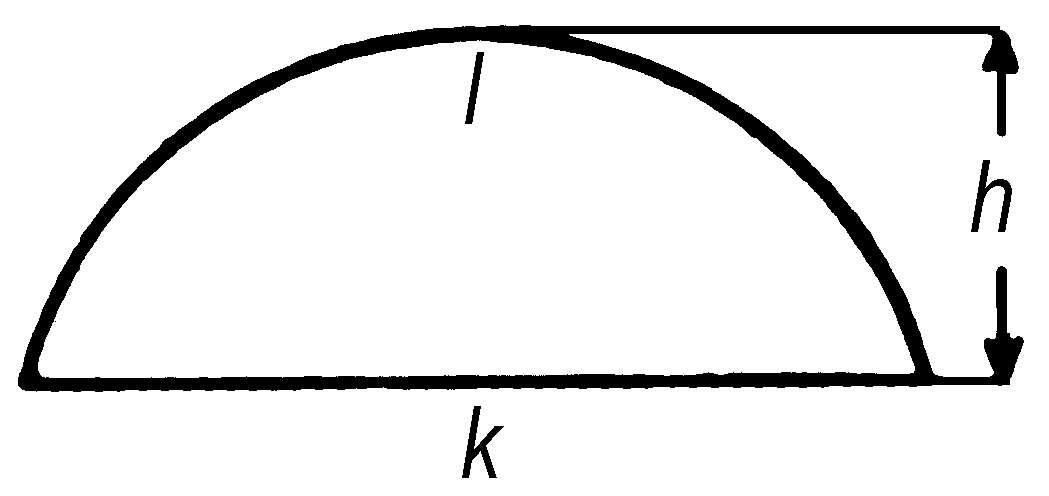
弓 形
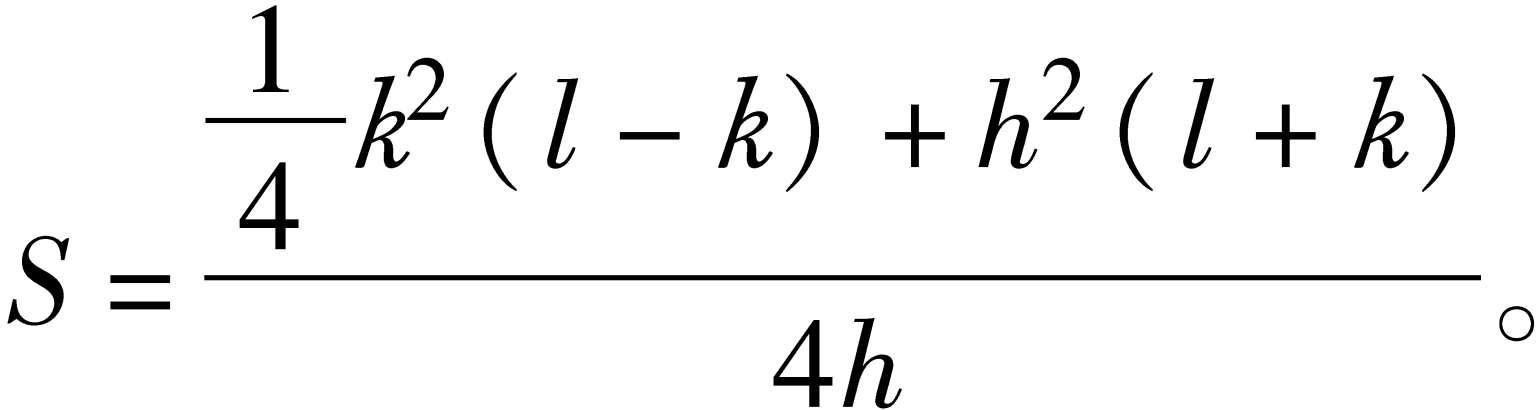
同心圆 圆心相同的一些圆。
圆环 两同心圆的圆周所夹的平面部分。
九点圆 三角形三边上的中点、三条高的垂足、垂心与三顶点的连线的中点,这九点必在一个圆周上,此圆称为三角形的“九点圆”。它是由 19 世纪初法国数学家庞斯莱发现的。后人对其研究曾风行一时,故有上百种证法。三角形九点圆的半径等于外接圆半径的一半,圆心在 * 欧拉线上。
尺规作图 利用直尺和圆规为工具,按照以下作图公法所允许的作法能完成的作图称为“尺规作图”。所谓作图公法,是指用直尺和圆规只能做到:(1)过两已知点作一直线;(2)确定两已知直线的交点;(3)已知圆心和半径作圆;(4)确定已知直线和已知圆的交点;(5)确定两已知圆的交点。凡是不能通过有限次作图公法所允许的作图来完成的作图问题,就称“尺规作图不能问题”。“三等分角问题”、“倍立方问题”、“化圆为方问题”都是著名的尺规作图不能问题。
三等分角问题 利用直尺和圆规把任意角三等分的问题。这是古希腊所谓几何三大问题之一。其余两个问题是:化圆为方问题,就是做出和一个已知圆有等面积的正方形的问题;倍立方问题,就是作体积为一个已知立方体二倍的立方体的问题。近代已经证明,在直尺只能作直线,圆规只能画圆弧的规定下,这三个问题都不可能解决,但在处理实际问题时可用近似方法做出。
倍立方问题 见“三等分角问题”(90页)。
化圆为方问题 见“三等分角问题”(90页)。
等周问题 当边界的长度(或面积)给定时,寻求有最大面积(或体积)的平面图形(或立体图形)这类问题的统称。可以证明,在周长一定的平面图形中,圆的面积最大;在表面积一定的封闭曲面中,以球面围成的立体(即球)的体积最大。
运动 指欧氏空间中点的一种变换,使得对任意两点间的距离在变换下保持不变。在欧氏几何中,运动可表为平移、旋转及镜像反射的合成。
合同变换 当两个图形中的一个可经过平移、旋转、反射(即“轴对称”和“平面对称”,参见“对称变换”)或它们的组合变为另一个时,则称这两个图形为“合同图形”,这个变换为“合同变换”。
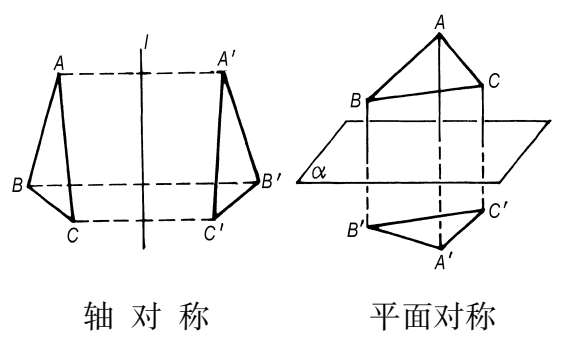
对称变换 一类几何变换。主要有三种:(1 )中心对称:将一个图形上各点到一定点O的射线延长一倍,延长线的端点所构成的图形称为与原图形关于点O成中心对称,称点O为“对称中心”。(2)轴对称:从图形上的各点作定直线l的垂线并延长一倍,延长线的端点所构成的图形称为与原图形关于直线l成轴对称,称l为“对称轴”。(3)平面对称:从一图形上的各点作一个定平面α的垂线并延长一倍,延长线的端点所构成的图形称为与原图形关于平面α成平面对称,称平面α为“对称平面”。
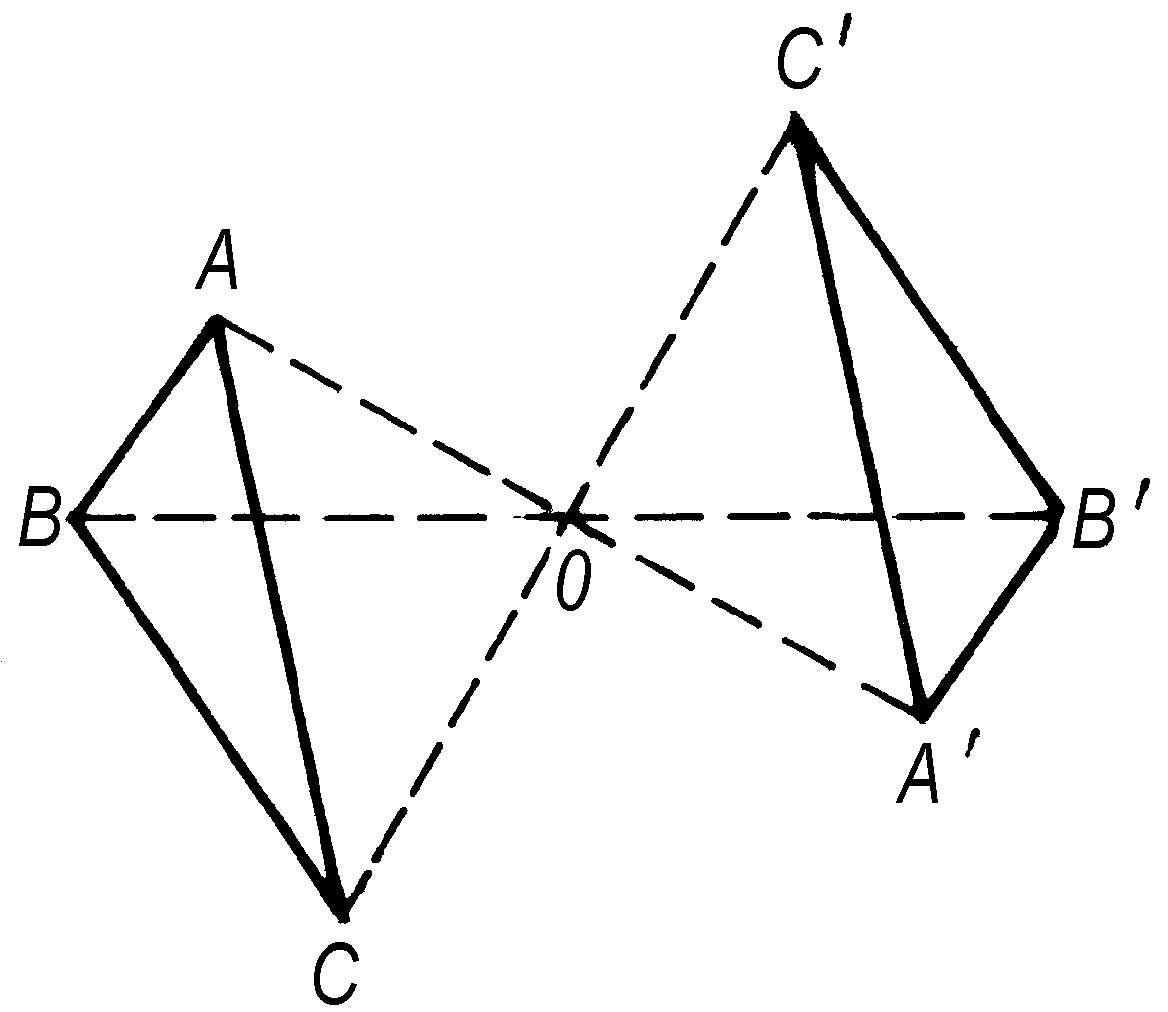
中心对称
对称变换
中心对称 见“对称变换”。
轴对称 见“对称变换”。
平面对称 简称“面对称”。见“对称变换”。
位似变换 在平面上或空间中的一种变换。规定:任一点A和它的对应点A′的连线都通过某一定点O,OA′和OA的比是一个常数。定点O称为“位似中心”,该常数称为“位似系数”,A和A′所画的图形互称为“位似图形”。如两个位似图形的各对对应点全在位似中心的同旁,互为“外位似”;如各对对应点全在位似中心的两旁,则互为“内位似”。
内位似
外位似
位似中心 见“位似变换”。
位似系数 见“位似变换”。
反演
在平面上或空间中取定点O和
任
意
一
点A,并在射线OA上取点A′,使
 (R是固定的正数),称A与A′互为“反演点”,O为“反演中心”,R为“反演半径”;从A变到A′或从A′变到A的变换称为“反演”。在反演中,直线变成直线或圆,圆变成圆或直线,相交两曲线的交角不变。
(R是固定的正数),称A与A′互为“反演点”,O为“反演中心”,R为“反演半径”;从A变到A′或从A′变到A的变换称为“反演”。在反演中,直线变成直线或圆,圆变成圆或直线,相交两曲线的交角不变。
二面角 通过定直线的两个“半平面”所夹的空间部分。直线称为二面角的棱。半平面称为二面角的面。
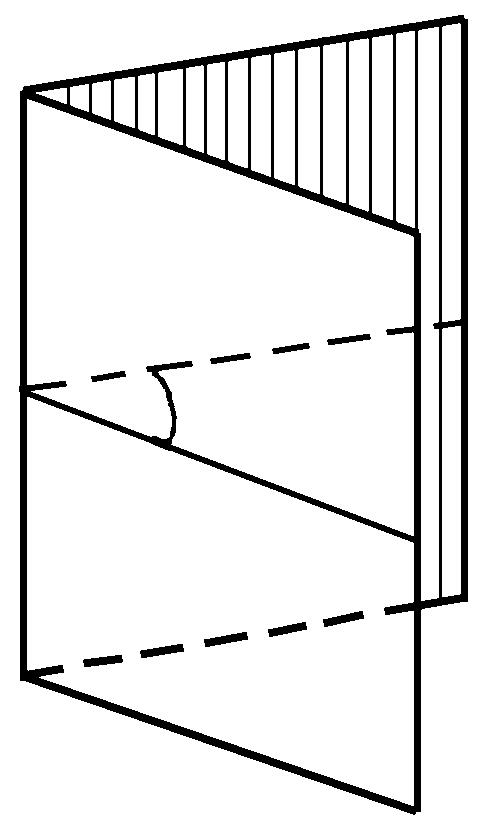
二面角
平面角 在二面角的棱上任取一点分别在各面内作垂直于棱的两射线,称它们的夹角为这二面角的“平面角”。
多面角 过平面外一点O向平面上的简单多边形的顶点引射线,所有相邻射线所夹的平面部分围成的立体图形。O称为多面角的“顶点”,射线称为“棱”,相邻两棱所夹的角称为“面角”,相邻两棱所夹的平面部分称为“侧面”。多面角按照它的侧面数目分别称为三面角、四面角等等。如果所给的多边形是凸的,则相应的多面角称为“凸多面角”,否则称为“凹多面角”。凸多面角的面角总和小于四个直角。
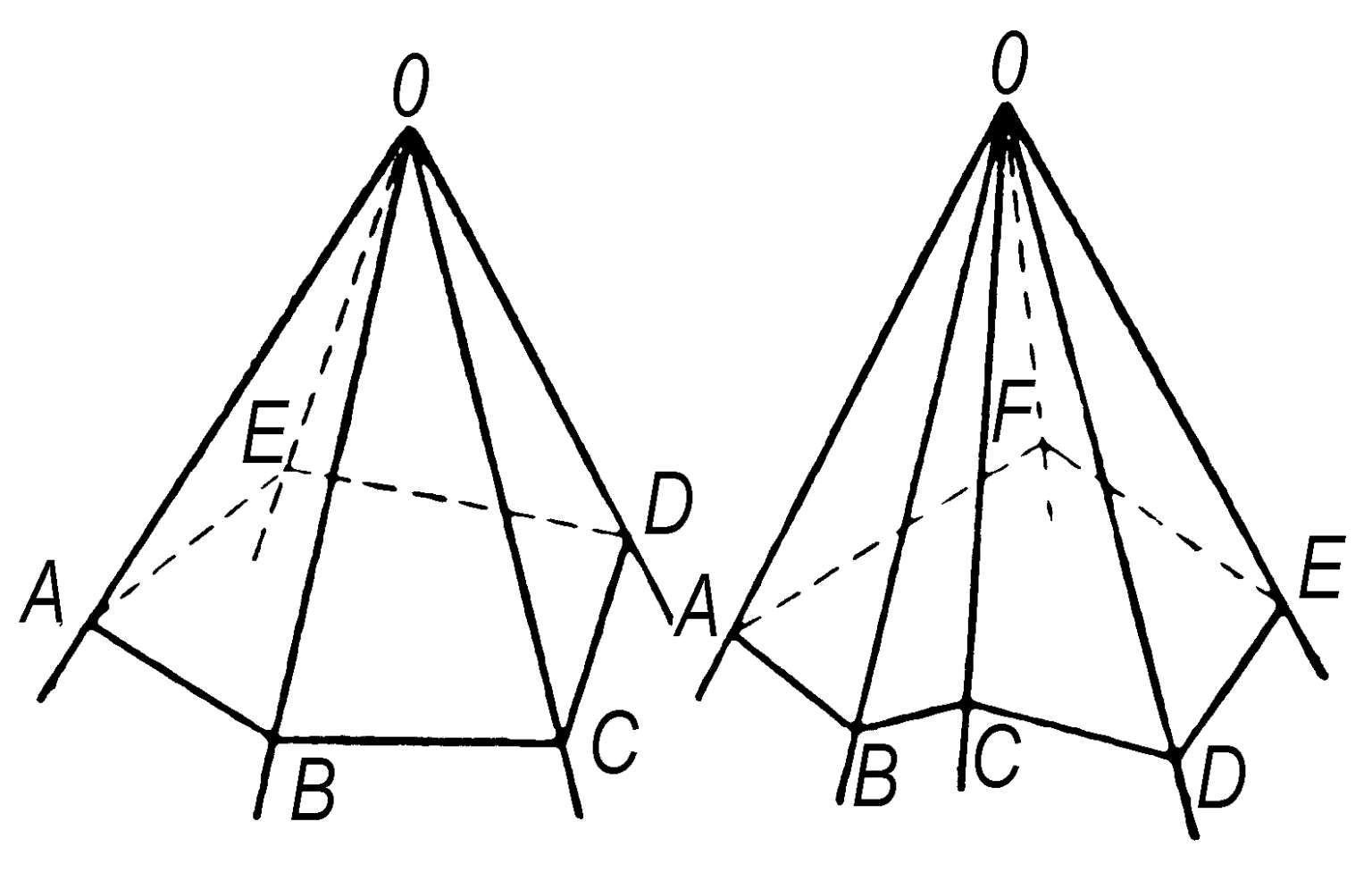
多面角
面角 见“多面角”。
多面体 指空间中由几个平面多边形所围成的立体。各个多边形称为多面体的“面”或“侧面”。相邻多边形的公共边称为“棱”。相交于同一点的几个面构成一个多面角。这一点称为顶点。不在同一面内的两顶点的连线称为“对角线”。多面体有几个面,就称为几面体。由几个相同的正多边形围成的立体称为“正多面体”。正多面体只有五种,即:(图中上下自左至右)正四面体、正六面体、正八面体、正十二面体和正二十面体。
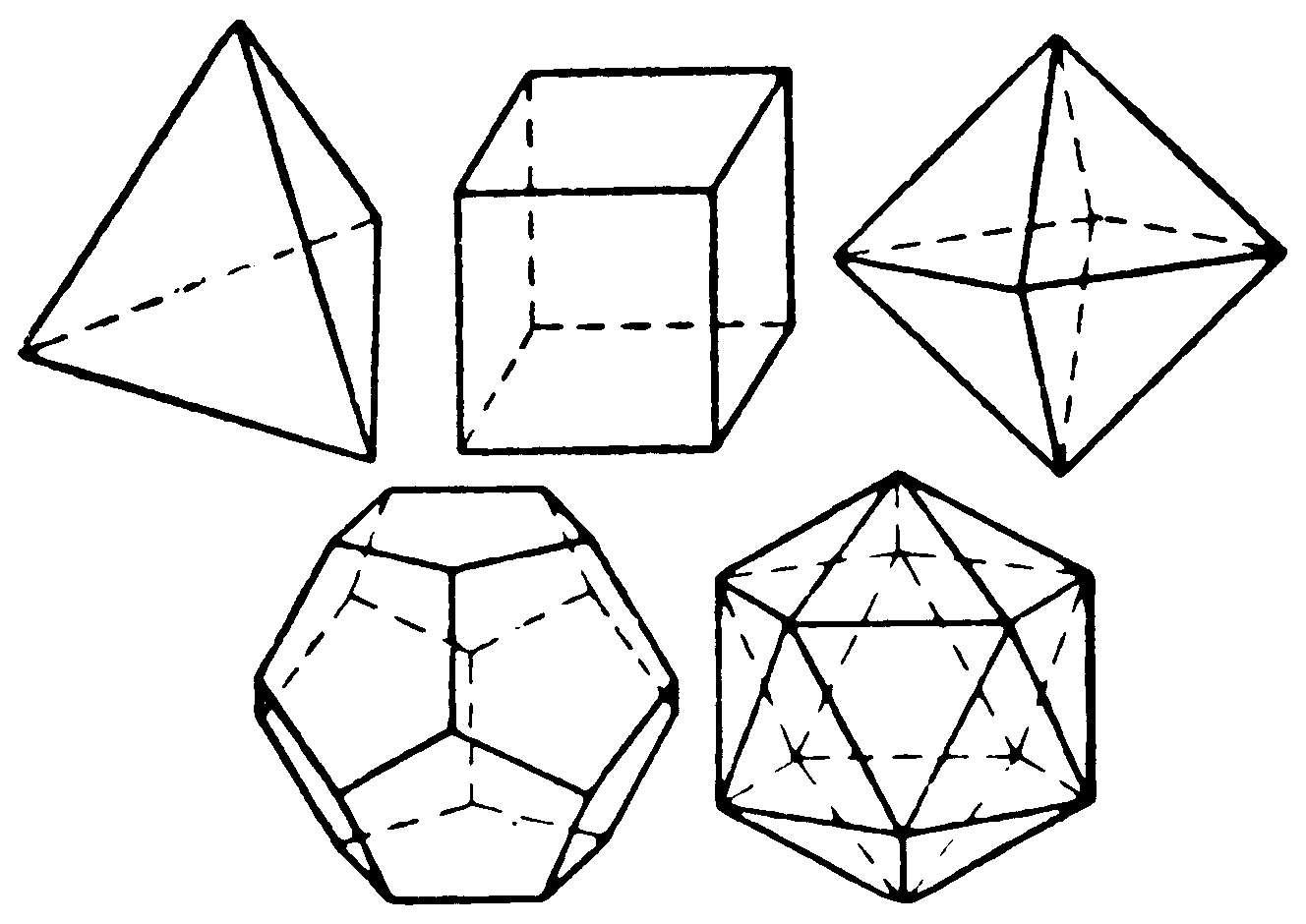
正多面体
凸多面体 一种特殊的多面体。在这种多面体的表面上任选两个不处于同一个面中的点,则此两点的连线全部包含在该多面体的内部。凸多面体的顶点数V、棱数E及面数F之间成立着下列公式(又称“欧拉公式”):V-E+F= 2。
四面体 由四个三角形面所围成的一种多面体。
正多面体 见“多面体”。
平行六面体 由六个平行四边形所围成的多面体。平行六面体分为斜平行六面体和直平行六面体两种。体积等于其底面积和高的乘积。
立方体 亦称“正方体”。各面均为正方形的平行六面体。立方体的所有棱长都相等。面积等于其棱长的立方。
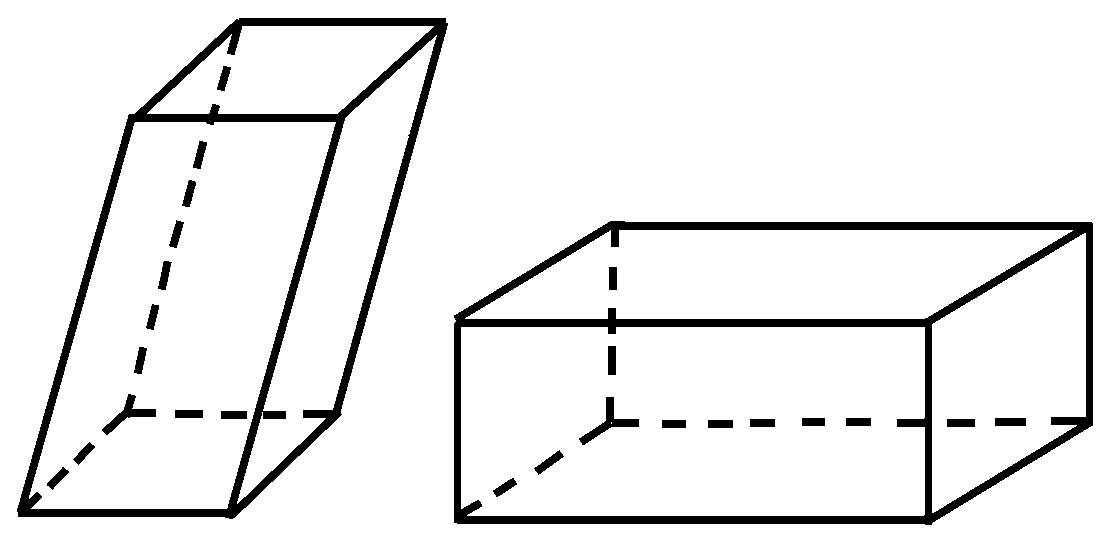
平行六面体
正方体 即“立方体”。
长方体 各面均为矩形的平行六面体。长方体中交于同一顶点的三条棱,分别称为长方体的长、宽、高,合称为三度。长方体对角线的平方等于其三度的平方和,体积等于其三度的乘积。
棱柱 亦称“角柱”。当一个多面体中有两面相互平行而其余每相邻两面的公共边也相互平行时,称此多面体为“棱柱”。两平行的平面称为棱柱的“底面”,其余的面称为“侧面”,相邻两侧面的公共边称为“侧棱”。两底面间的距离称为“高”。侧棱斜交于底面的棱柱称为“斜棱柱”,侧棱垂直于底面的棱柱称为“直棱柱”,底面为正多边形的直棱柱称为“正棱柱”。直棱柱的侧面积等于底的周长和侧棱长度的积,棱柱的体积等于它的底面积乘高。
斜棱柱
正棱柱
角柱 即“棱柱”。
棱锥 亦称“角锥”。当一个多面体的一个面是多边形,而其余各面是有公共顶点的三角形时,称为“棱锥”。称多边形为棱锥的“底面”,其余各面为“侧面”,侧面的公共顶点为棱锥的“顶点”,顶点与底面间的距离为“高”。当底面为正多边形,而高通过底面中心时,称为“正棱锥”。正棱锥的侧面三角形(过棱锥的顶点)的高称为“斜高”。棱锥的体积等于高与底面积的乘积的三分之一,正棱锥的侧面积等于斜高与底的周长乘积的一半。
斜棱锥
正棱锥
角锥 即“棱锥”。
棱台 亦称“角台”。以平行于棱锥底面的平面截棱锥,底面和截面之间的部分。
拟柱体 所有顶点都在两个平行的平面内的多面体称为“拟柱体”。其中平行的两个多边形面称为拟柱体的底面,其余的面(一般为三角形、平行四边形或梯形)称为拟柱体的侧面,两底面之间的距离称为拟柱体的高,通过高的中点且平行于底面的截面称为拟柱体的中截面。设S 1 、S 2 和S 0 分别为拟柱体两底面和中截面的面积,h为它的高,则其体积是
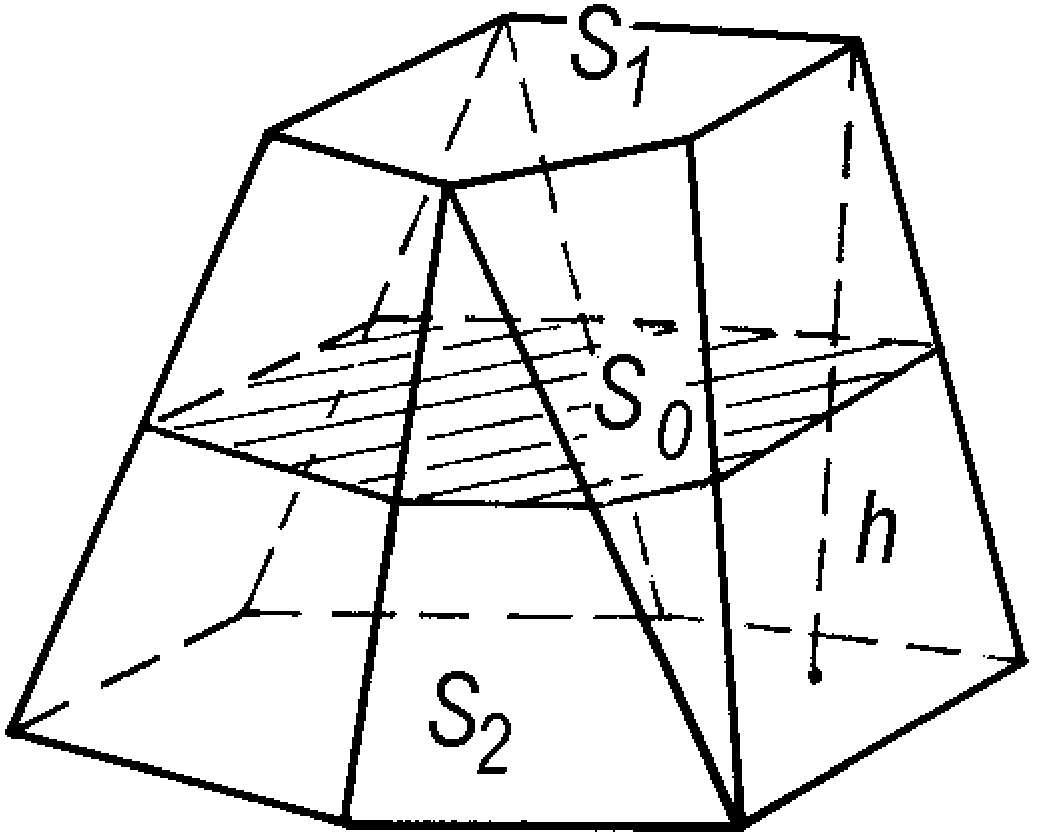
拟柱体
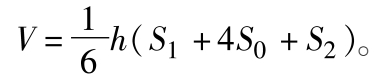
棱柱、棱锥、棱台都可看作拟柱体的特殊情况,它们的体积公式可统一在拟柱体的体积公式中。
画法几何 旧称“投影几何”。几何学的一个分支。用投影的方法研究在平面上图示、图解空间形体的规律和方法的学科。是工程制图的理论基础。
视图 在工程制图中,将物体按正投影法向投影面投射时所得到的投影图。有第一角画法和第三角画法之分。在第一角画法中,光线自物体的前面向后投射所得的投影称“主视图”,自上向下投射所得的称“俯视图”,自左向右投射所得的称“左视图”;从其他三个相反方向投射所得的投影分别称“后视图”、“仰视图”和“右视图”。为完整地表达一个物体的形状,常须采用两个或更多的视图。
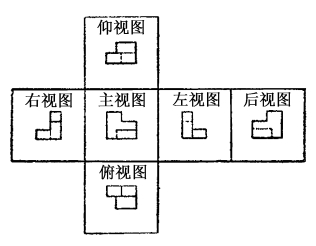
六个视图相对位置
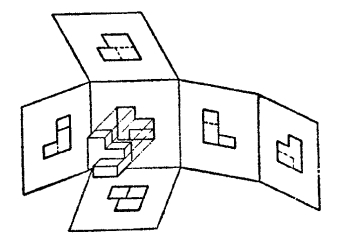
六面视图展开示意
透视图 亦称“透视投影”。按中心投影原理绘出的物体的图形。同样大小的物体在图中呈现出远小近大。空间任意方向的平行线(平行于投影面者除外)在透视图上都有一聚集点,如平行的直的铁路轨道在图中远处相遇。立体感极强。在土木建筑等工程中应用较多。

透视图
投影 画法几何中,用一组假想光线将物体的形状投射到一个面上去而得到该物体轮廓形状的方法。在该面上得到的图形,也称“投影”。这个面称“投影面”(通常是平面)。投射线从一点出发的称“中心投影”,该点称“投影中心”。投射线相互平行的称“平行投影”。平行投影中,投射线与投影面垂直的称“正投影”;倾斜的称“斜投影”。
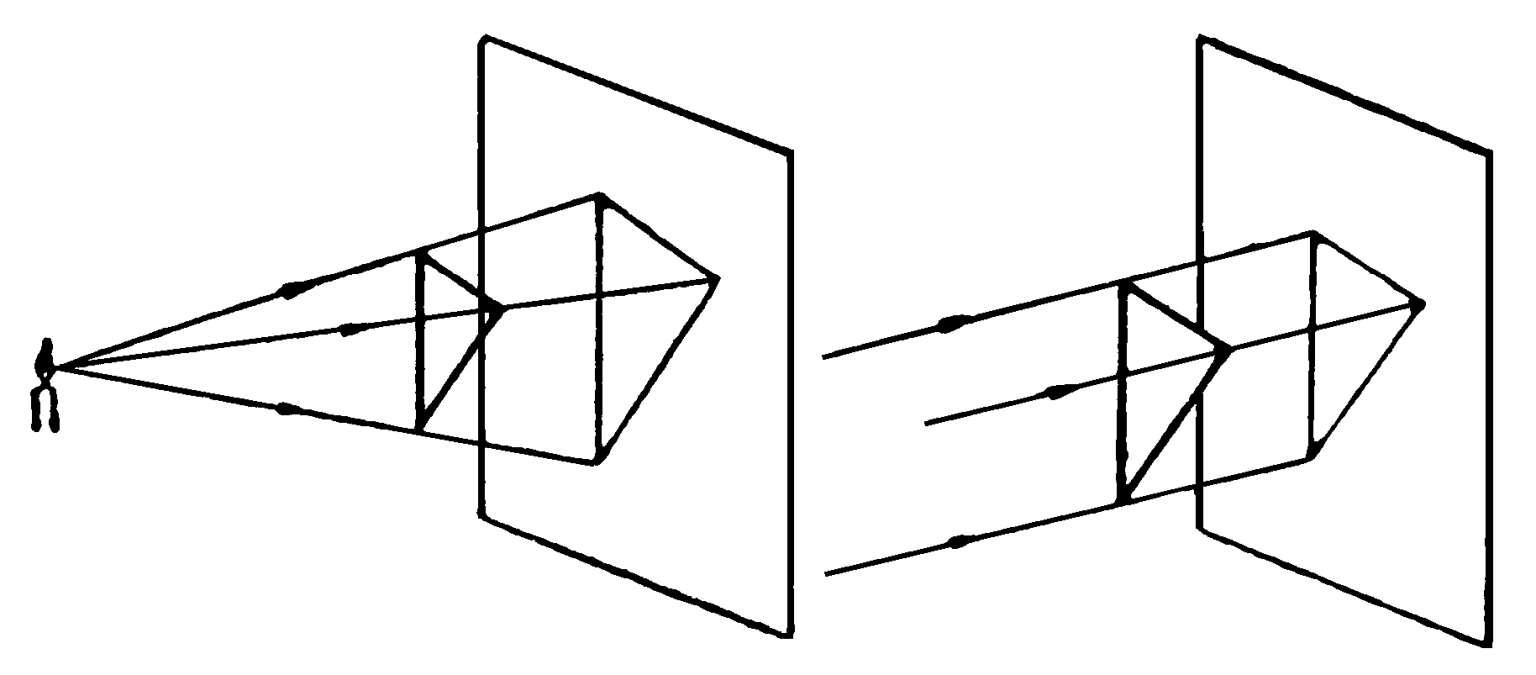
中心投影平行投影
中心投影 见“投影”。
平行投影 见“投影”。
正投影 见“投影”。
斜投影 见“投影”。
立体图 泛指具有立体感的图,如轴测图、透视图等。另有根据双眼看物原理,用两个中心(或视点)投射出同一物体的两个投影,错开叠画在同一图上的,称“双心透视图”。看图时需戴上专用眼镜(如红绿眼镜),才能显示出物体和所处空间的实像,使人看了有身历其境之感。立体图在工程、科学技术和教学中普遍应用。
剖视图 简称“剖视”。假想把物体切去一部分后绘出的其余下部分的视图。常用来表达物体内部的结构。所绘出的视图曾被称为“剖面”或“剖面图”。在机械制图以外的其他场合中,尚多沿用“剖面”或“剖面图”的名称。且“剖面”、“剖面图”、“断面”、“断面图”常被通用而不予严格区分。但有的学科对这些名称有自己的习惯用法。
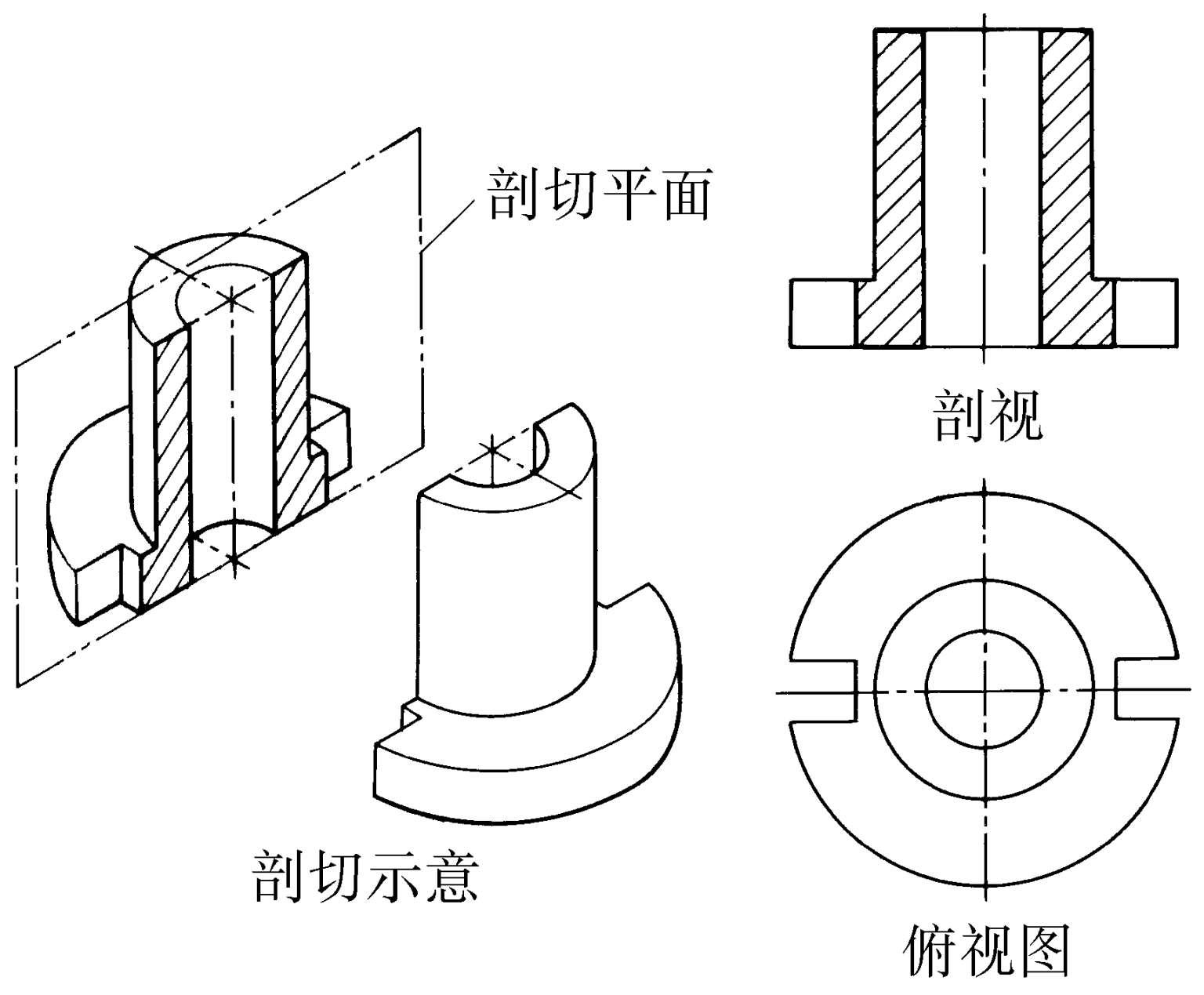
剖视图
剖面图 ❶简称“剖面”。在机械制图中,假想用一个面将物体的某部分切断,所绘出的该切断表面形状的图形。❷机械制图中“剖视图”的旧称。现其他学科仍多沿用。
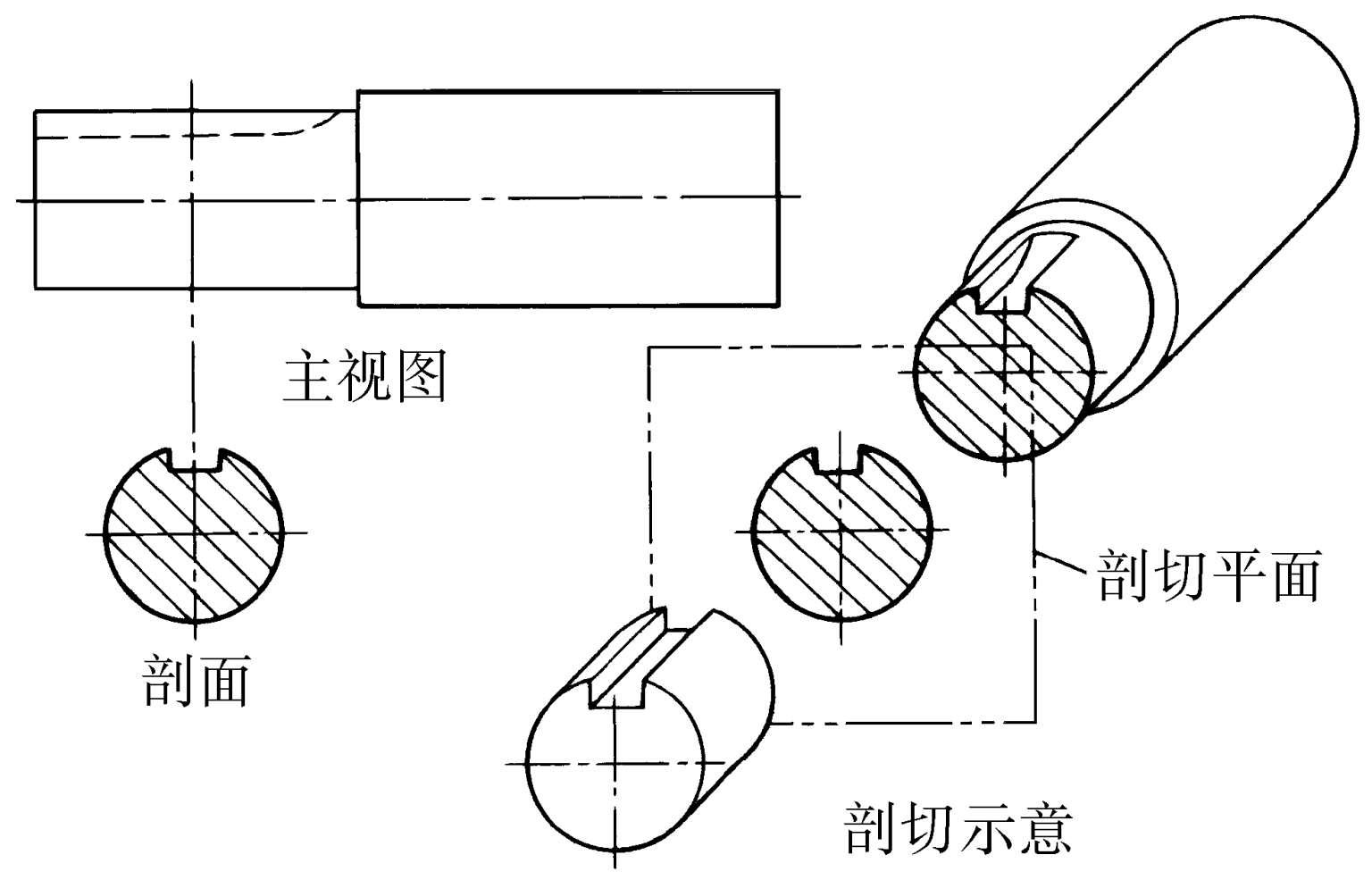
剖面图
轴测投影 平行投影的一种。将物体的三个坐标面放在与投射线都不平行的位置,使物体的三个坐标面在一个投影面上都能反映出来并具有立体感。这样绘出的图形,称为“轴测图”。物体上与任一坐标轴平行的长度,在轴测图中均可按一定的比率来量度。三轴向的比率都相同时称为“等测投影”,其中两轴向比率相同时称为“二测投影”,三轴向比率均不同时称为“三测投影”。轴测投影中投射线与投影面垂直的称为“正轴测投影”,倾斜的称为“斜轴测投影”。轴测图在工程技术及其他学科中常有应用。
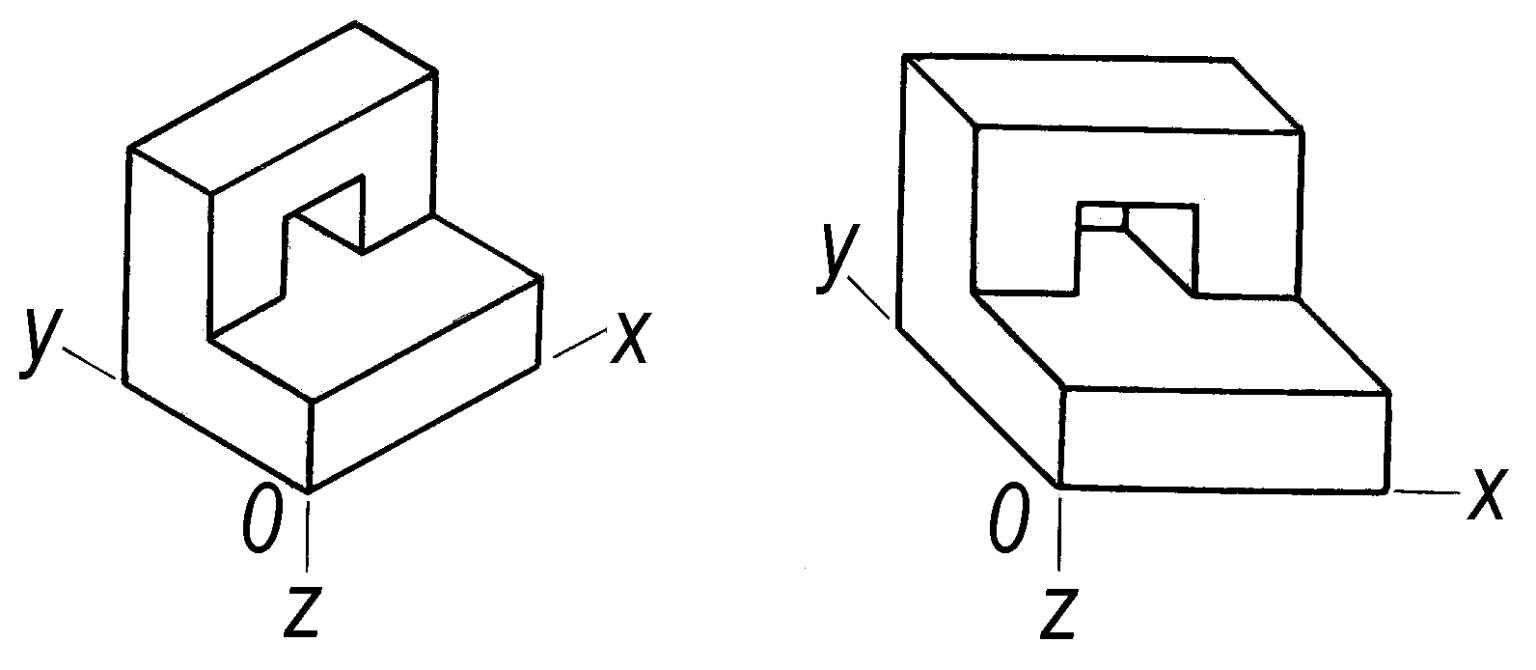
正轴测投影图斜轴测投影图
等测投影 见“轴测投影”。
二测投影 见“轴测投影”。
三测投影 见“轴测投影”。
坐标 确定平面上或空间中一点位置的一组有序数。例如,在平面上,取点O为原点,过点O引互相垂直的两直线x′Ox、y′Oy,称为坐标轴,从一点P作它们的垂线PM、PN。设从点O到垂足M和N的距离是︱x︱和︱y︱,视垂足M在点O的右或左,N在点O的上或下而规定x和y为正或负。称(x,y)为点P在笛卡儿直角坐标系Oxy下的坐标,简称“直角坐标”。在空间中的直角坐标是用三个数(x,y,z)来表达的。即取一点O为原点,从O引互相垂直的三直线x′Ox、y′Oy、z′Oz,作为坐标轴。从点P作这三轴的垂线,x、y、z的绝对值就是点O到三个垂足L、M、N的距离,x、y、z的正或负要看L、M、N在各轴的前或后、右或左、上或下来决定。除了直角坐标以外,常用的还有极坐标、球面坐标、柱面坐标等。
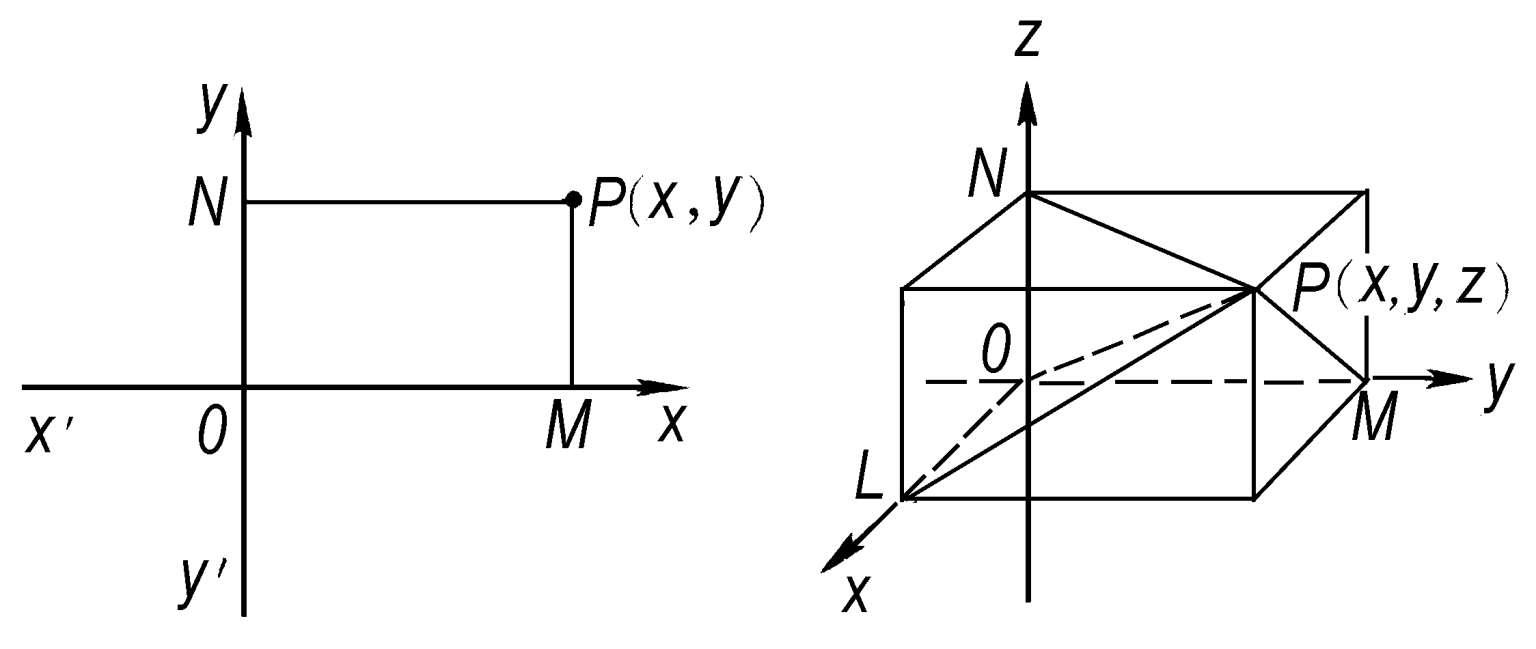
平面直角坐标空间直角坐标
直角坐标 亦称“笛卡儿坐标”。见“坐标”(94 页)。
斜角坐标 当平面上两坐标轴相交成任意角ω时,就构成斜角坐标系(参见“坐标”)。对该坐标平面上任一点P,分别作两坐标轴的平行线,交x轴于M,交y轴于N,OM=x,ON=y,则有序数对(x,y)就称为点P的斜角坐标(如图)。直角坐标是斜角坐标的一种特殊情况。
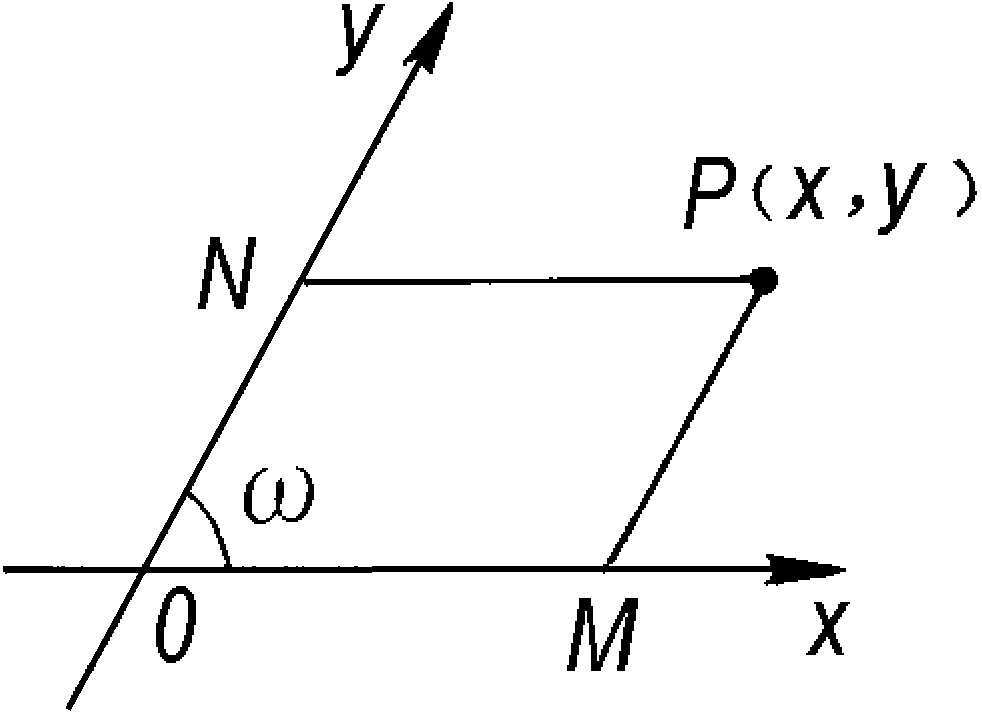
斜角坐标
象限 平面直角坐标系的两坐标轴分平面为四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ,分别称为第一、第二、第三、第四象限(如图)。
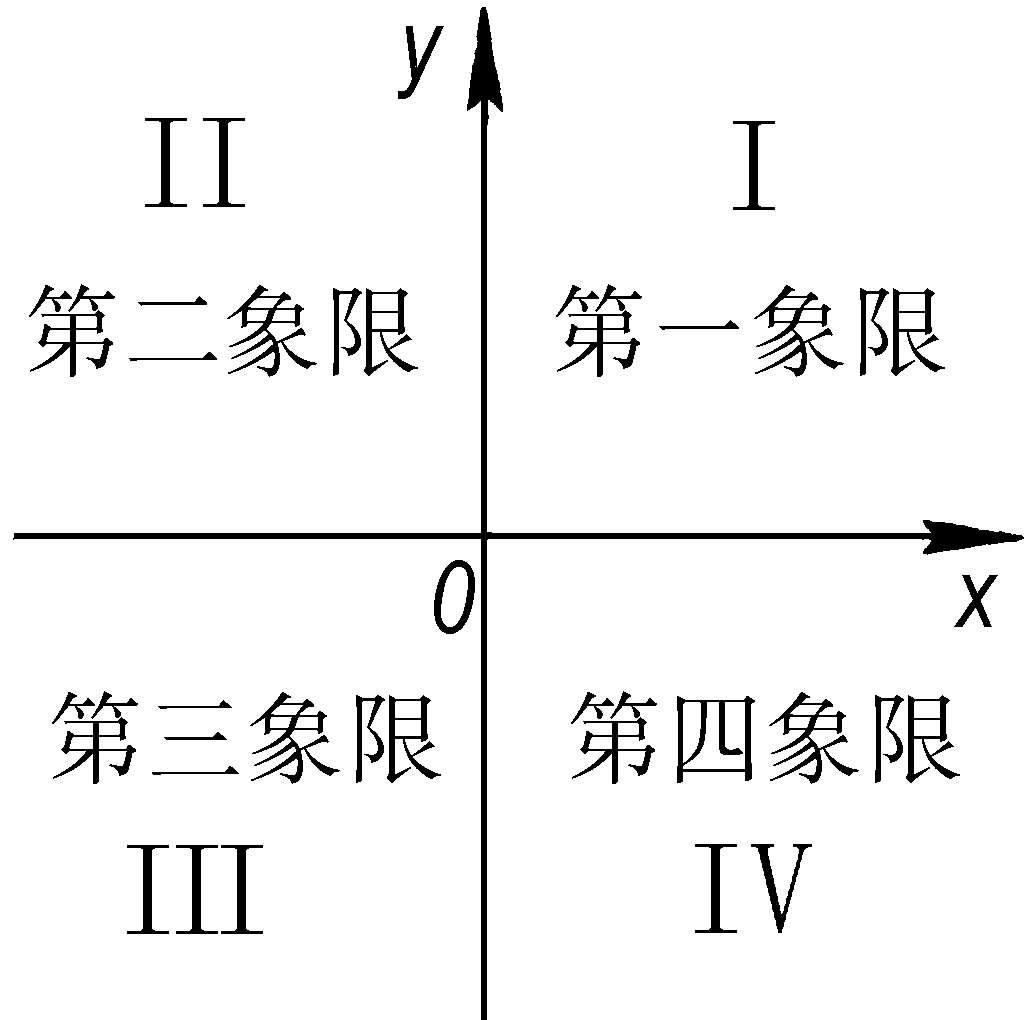
象 限
卦限 空间直角坐标系的三个坐标面,把空间分成八个部分,每一部分称为一个“卦限”。在xOy平面的上方和下方分别按逆时针序依次为第Ⅰ ~第Ⅳ,第Ⅴ ~第VIII卦限(如图)。
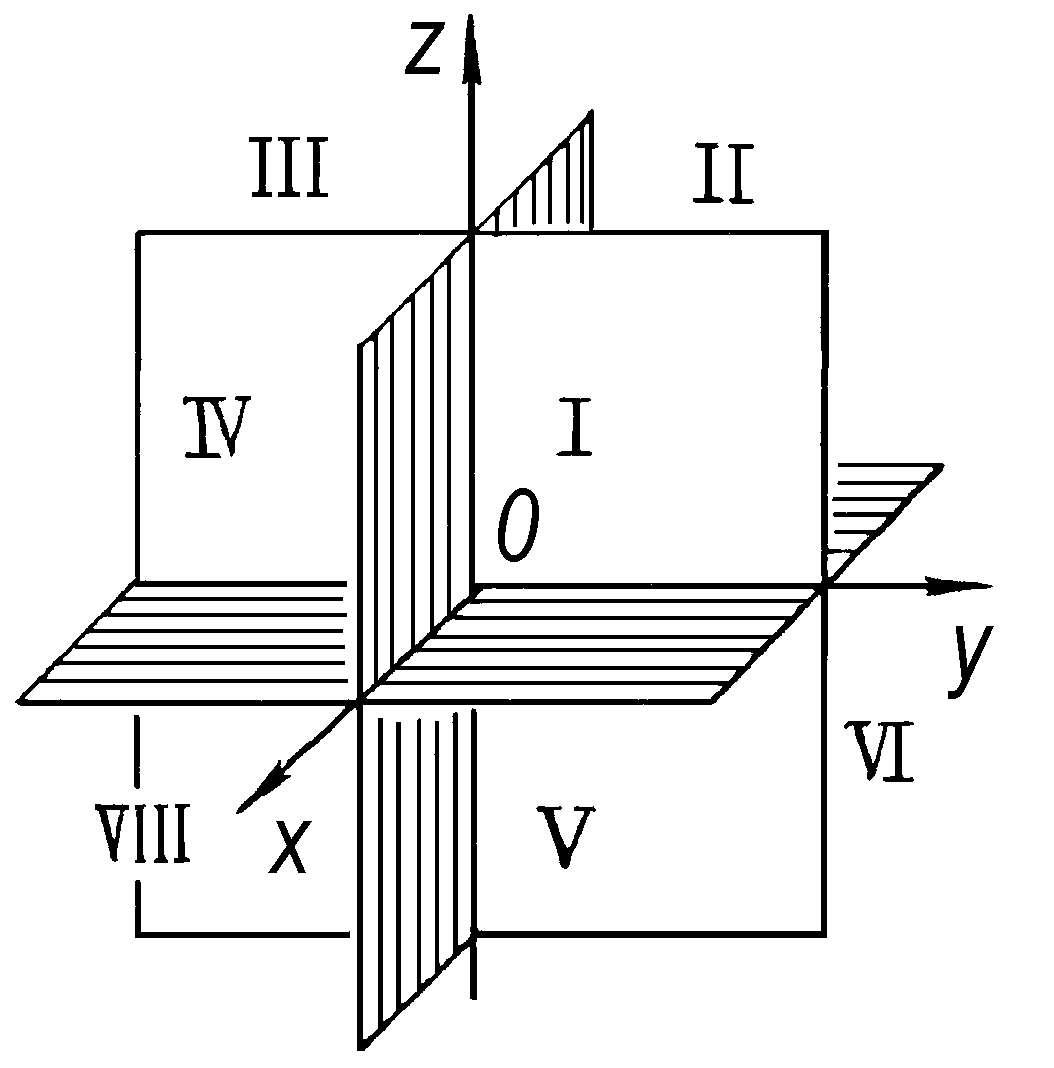
卦 限
方向余弦 设从空间直角坐标系的原点O发出的射线和x、y、z轴的交角分别是α、β、γ,则称cosα、cosβ、cosγ为这射线的“方向余弦”。它们之间有关系式
极坐标 平面坐标的一种。在平面上,取一点O称为“极”,从O出发的一射线Ox称为“极轴”。平面上任意一点P的位置,就可用线段OP的长度r和OP与Ox所夹的角θ来确定(如图)。(r,θ)称为点P的“极坐标”,r为“矢径”,θ为“极角”。
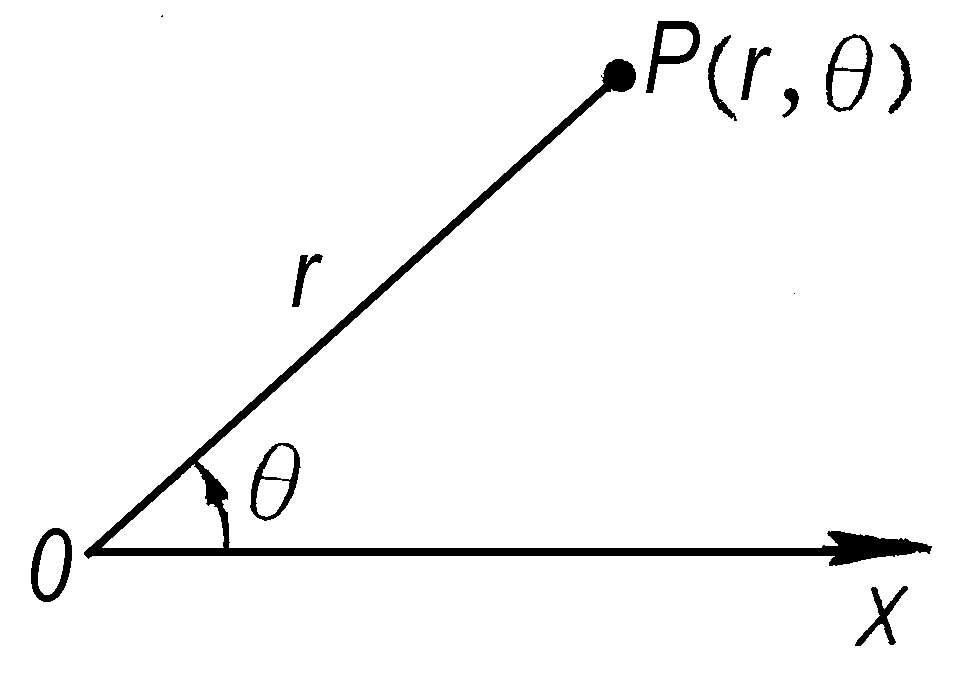
极坐标
极轴 见“极坐标”。
矢径 见“极坐标”。
柱面坐标 空间坐标的一种。当给定一个直角坐标系O-xyz时,空间中一点P的柱面坐标是一组数(r,θ,z),其中r、θ是点P在xOy平面上的投影R的 * 极坐标,︱z︱是P到平面xOy的距离;当P在xOy的上(或下)方时,z是正(或负)的。
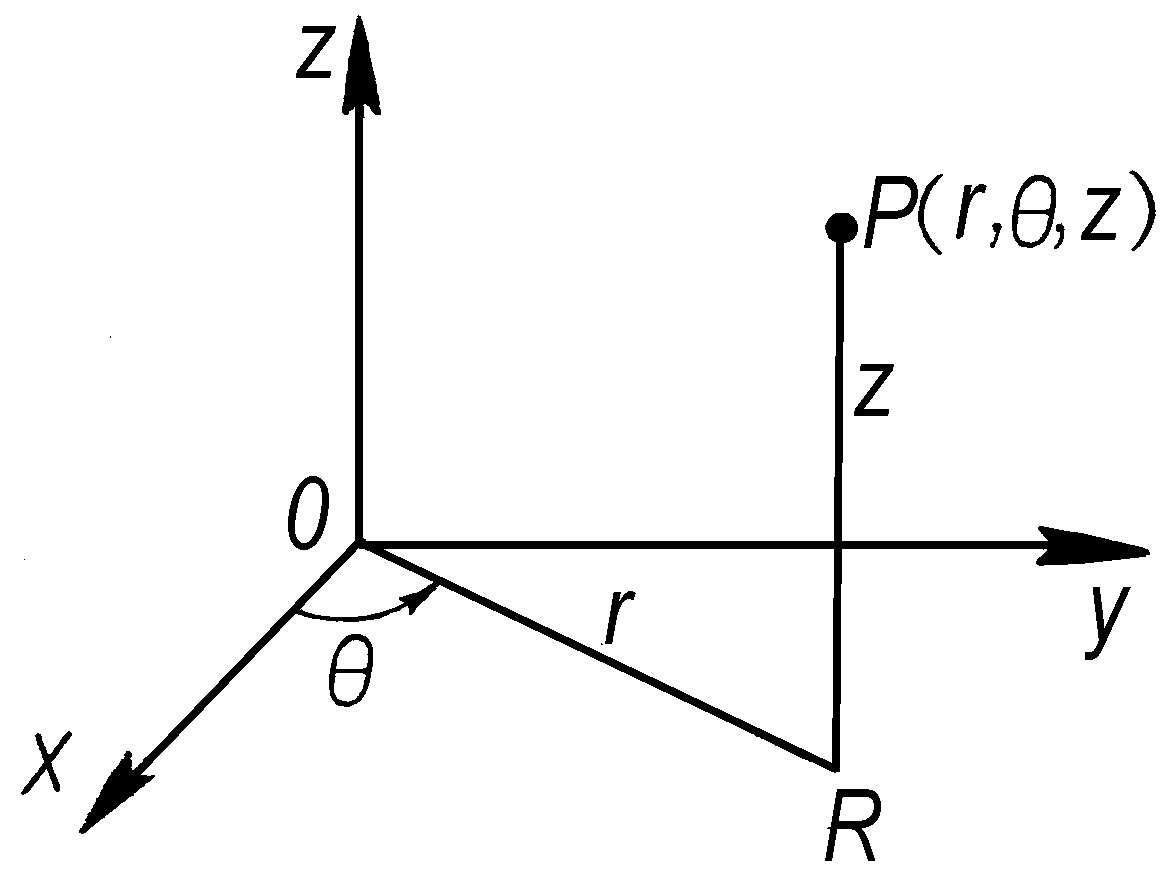
柱面坐标
球面坐标
空间坐标的一种。当给定一个直角坐标系O-xyz时,空间中一点P的球面坐标是一组数(r,θ,φ),其中r是点P到原点O的距离,θ是正向Oz轴与射线OP的夹角(0 ≤θ≤
 ),φ是正向Ox轴和OP在xOy平面上的投影OR所夹的角(0≤φ≤2
),φ是正向Ox轴和OP在xOy平面上的投影OR所夹的角(0≤φ≤2
 )。
)。
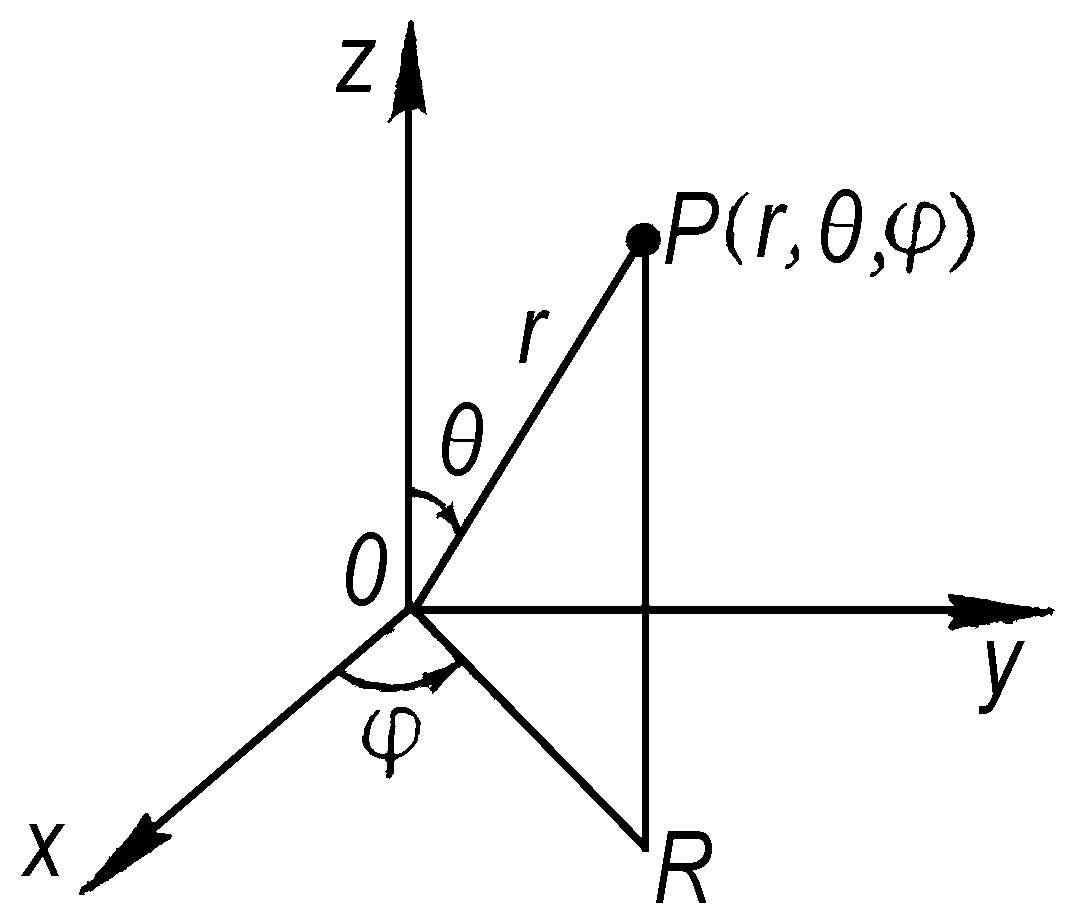
球面坐标
坐标变换 对于不同的坐标系,同一点所对应的两组坐标间的变换。例如,直角坐标间的变换,直角坐标和极坐标间的变换等。
向量 亦称“矢量”。既有大小,又有方向的量。可用带有方向的线段来表示,线段的长度代表向量的大小,称为向量的长度或向量的模。如力、速度、电场强度等物理量都是向量。向量运算和一般数字运算不同,如向量相加应按平行四边形法则进行,向量相乘则在不同情况下分别按向量积和数量积的方法进行。
矢量 即“向量”。
数量积
亦称“内积”、“点积”,物理学上常称为“标量积”。对两个向量
a
=
OA
,
b
=
OB
,将
OA
在
OB
上的投影与
OB
的长度相乘,称所得的乘积为
a
、
b
的数量积;记作
a
·b
。设
a
和
b
的交角为θ,则
a
·
b
=
 。例如机械功等于力
F
和位移
S
的标量积
F
·
S
。
。例如机械功等于力
F
和位移
S
的标量积
F
·
S
。
向量积
亦称“矢量积”、“外积”或“叉积”。对于两个向量
a
=
OA
,
b
=
OB
,从O作一向量
OC
,它和平面OAB垂直,其长度等于三角形OAB的面积数值的两倍,即
 =
=
 sinθ(θ为向量
a
和
b
的交角);而方向是这样决定的:当右手拇指指向
OA
,食指指向
OB
时,
OC
取中指所指的方向。这样从
a
、
b
作出的向量
c
(=
OC
),称为
a
到
b
的向量积,记作c = a × b。
sinθ(θ为向量
a
和
b
的交角);而方向是这样决定的:当右手拇指指向
OA
,食指指向
OB
时,
OC
取中指所指的方向。这样从
a
、
b
作出的向量
c
(=
OC
),称为
a
到
b
的向量积,记作c = a × b。
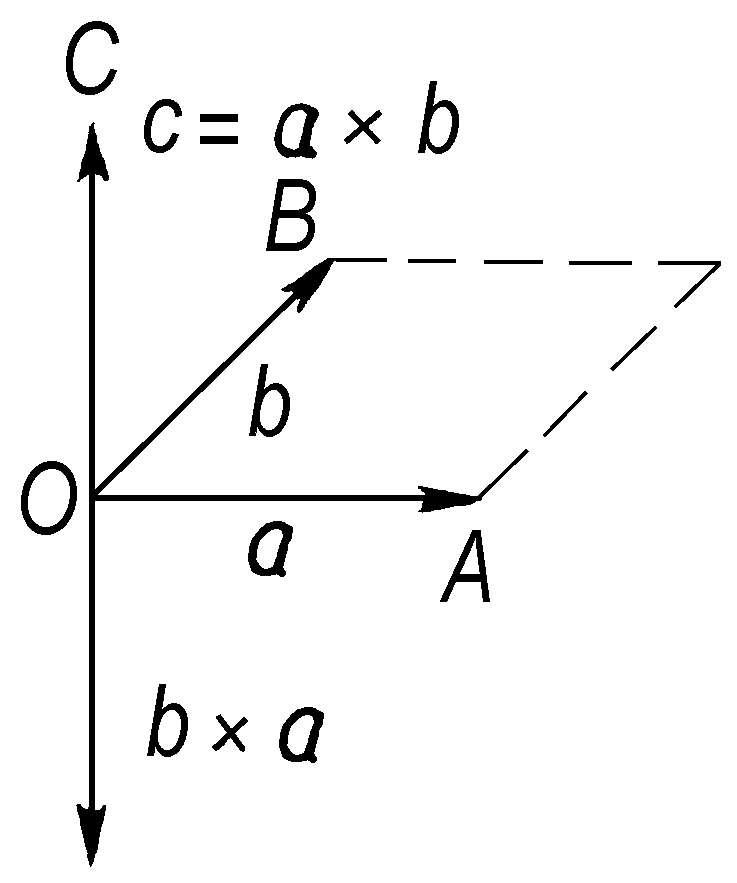
向量积
内积 即“数量积”。
外积 即“向量积”。
张量 向量概念的一种推广。在一个坐标系之下,由若干个数来表示的一种量;这些数称为“分量”。当从一坐标系改变为另一坐标系时,张量的分量应满足一定的变换规律。在近代数学和物理学中有广泛的应用。
分点 在通过两点A、B的有向直线上取一点P,使有向线段AP与PB之比等于定数r,则称P为分线段AB成定比r的“分点”。当r> 0 时,P在A、B之间,称为“内分点”;当r< 0 时,P在A、B之外,称为“外分点”。
调和点列 设Q 1 、Q 2 分别是线段P 1 P 2 的内分点和外分点,当四个有向线段P 1 Q 1 、Q 1 P 2 、P 1 Q 2 、Q 2 P 2 有关系

调和点列
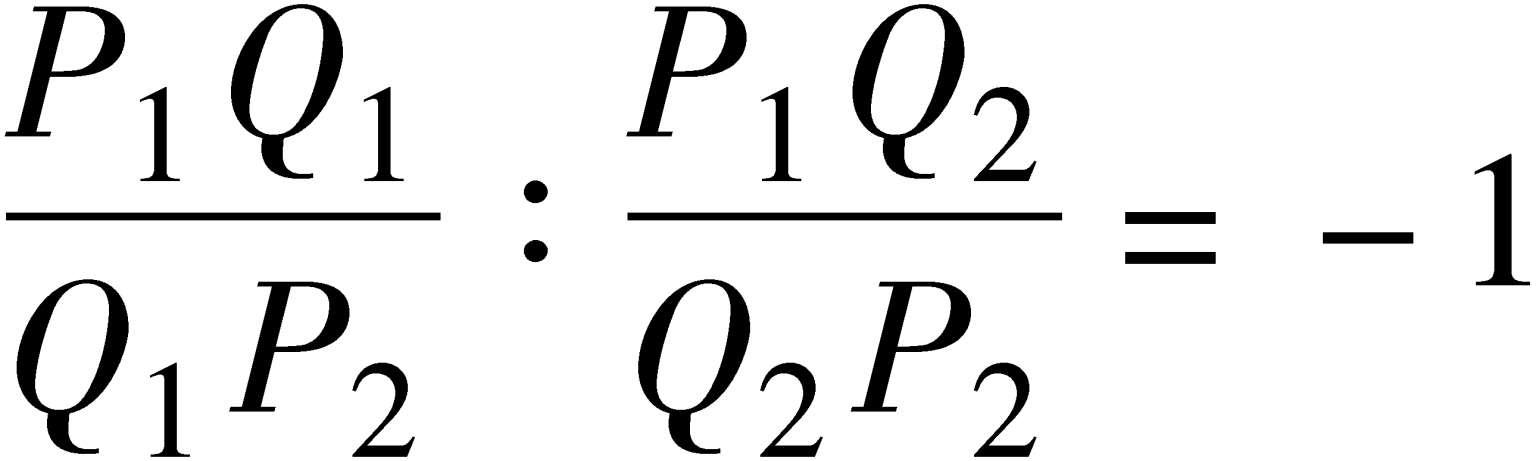
时,P 1 、P 2 、Q 1 、Q 2 称为“调和点列”。Q 1 、Q 2 称为关于点P 1 、P 2 的“调和共轭点”,或称Q 1 、Q 2 调和分割P 1 P 2 。
射影空间 射影几何学研究的基本对象。平面上过一定点O的直线构成了一族射影直线。如用一条不过点O的直线l去相截这族过点O的直线(如图),则l上的各点都对应了一条过点O的直线,唯独过点O的、与l平行的直线与l没有交点,于是这条独特的直线就被理解为直线l上的“无穷远点”。因而射影直线就能表现成直线l上的各点与所添加的“无穷远点”的总和。我们可用过点O的直线上任一点的 2 维坐标来作为射影直线上相应点的齐次坐标,可见齐次坐标可允许相差一个非零的倍数。类似地,射影平面是过三维空间中一定点的所有直线的全体,射影空间是过四维空间中一定点的所有直线的全体。
无穷远点 见“射影空间”。
交比 由射影直线上的四个点所确定的一个数量。设P 1 、P 2 、P 3 、P 4 是射影直线上的四个点,它们的齐次坐标分别为(x 1 ,y 1 )、(x 2 ,y 2 )、(x 3 ,y 3 )、(x 4 ,y 4 ),则由这四个点所确定的交比为
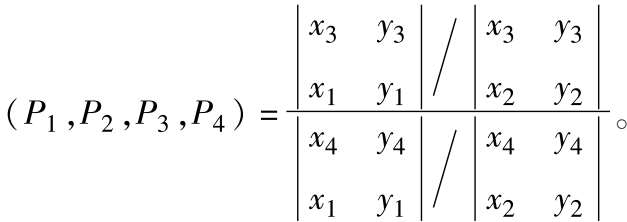
对偶原理 射影几何中的一个基本原理。如果我们把射影几何的一个命题中所涉及的点改换成线,线改换成点,几点共线改换成几线共点,几线共点改换成几点共线,则得到了原命题的对偶命题。对偶原理表明:如果原命题成立,则其对偶命题也成立。
德沙格定理 射影几何中的一个重要定理。由法国数学家德沙格发现。如果两个三角形的对应顶点的连线交于一点,则其三对对应边的交点必共线。具有上述条件的两个三角形称为透视三角形,其对应顶点连线的交点称为透视中心,对应边交点所在直线称为透视轴。本定理的逆定理亦真。
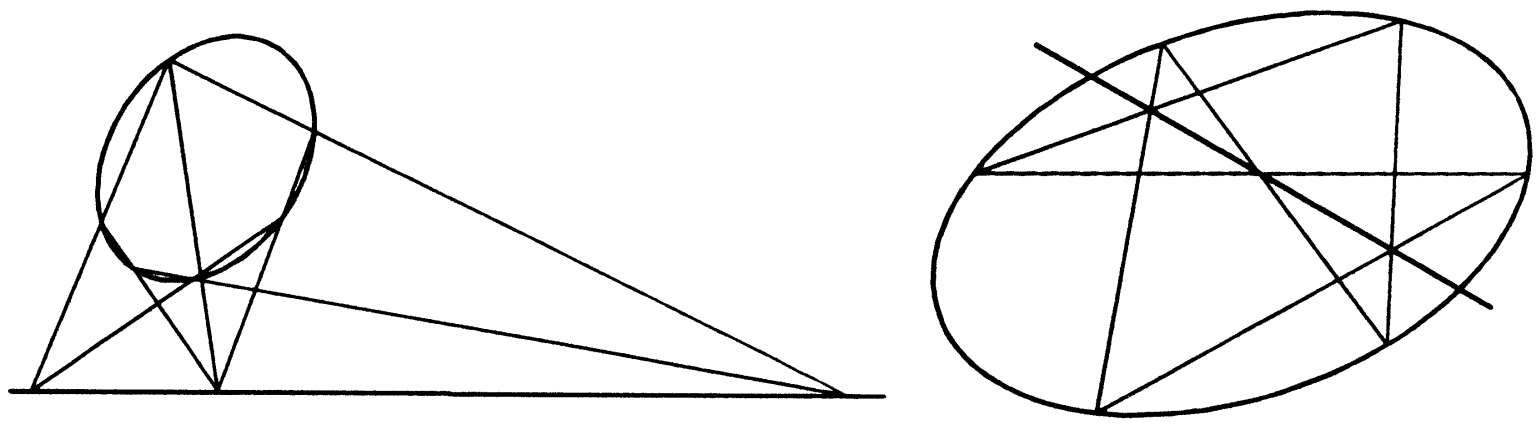
帕斯卡定理 布立安香定理的对偶命题。由法国数学家帕斯卡于 1640 年发现。圆锥曲线的内接六边形的三组对边的交点必位于一条直线上。称这条直线为帕斯卡线。
帕斯卡定理
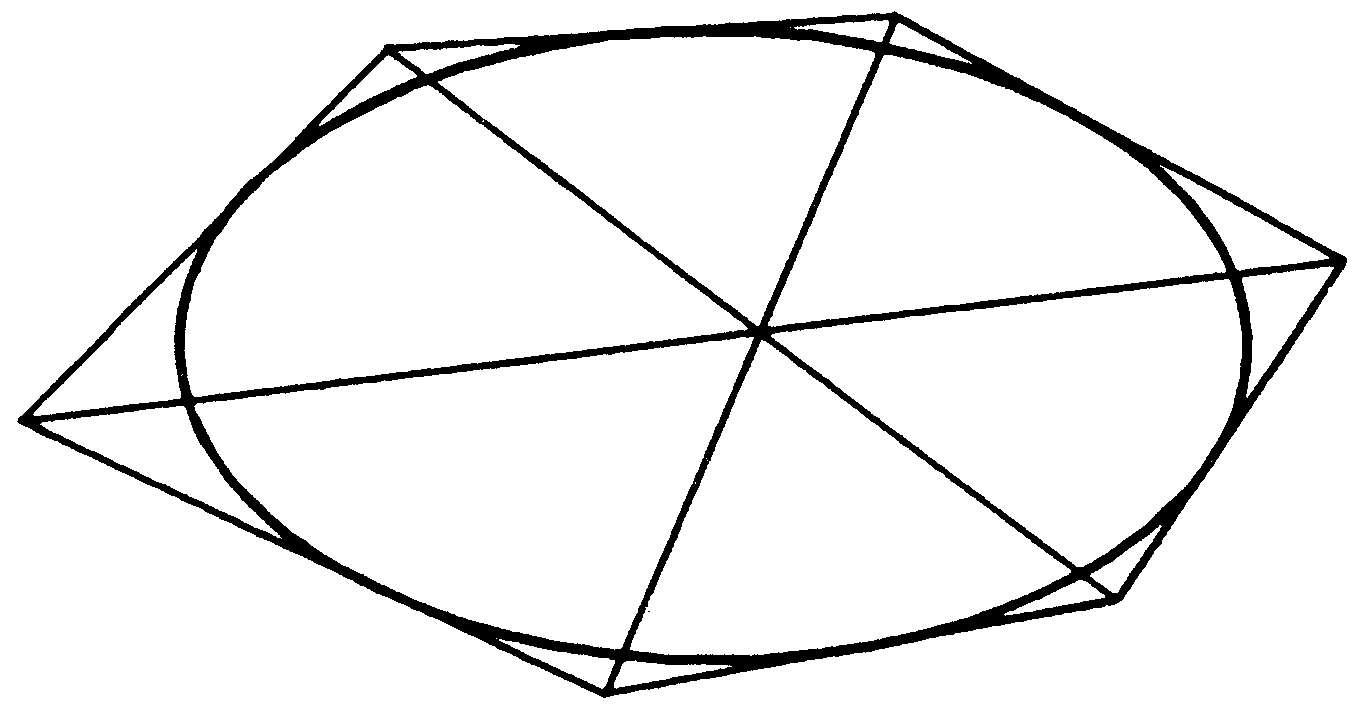
布立安香定理 帕斯卡定理的对偶命题。由法国数学家布立安香(Charles-Julien Brianchon,1783—1864)于 1806 年发现。圆锥曲线的外切六边形的三组对顶点的连线必交于一点。
布立安香定理
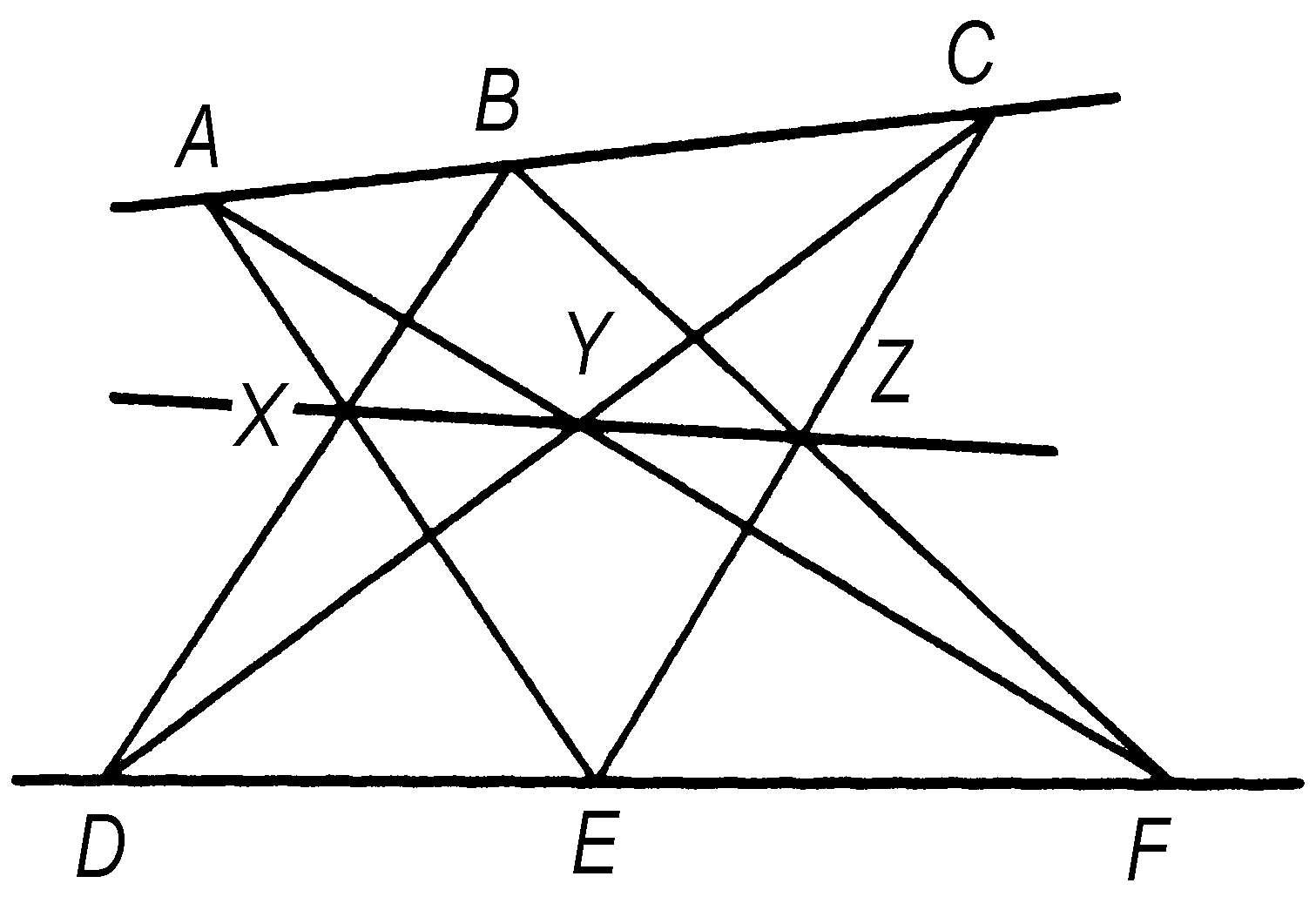
帕普斯定理 射影几何中的一个重要定理。由古希腊数学家帕普斯(Puppusof Alexandra,约300—约 350 )首先发现。如果A、B、C是一条直线上的三个点,D、E、F是另一条直线上的三个点,且AE和BD交于X,AF和CD交于Y,BF和CE交于Z,则X、Y、Z三点是共线的。帕普斯定理可视为帕斯卡定理的退化情形。
帕普斯定理
仿射空间 仿射几何学研究的基本对象。是欧氏几何中平面概念的一种推广。设V是域K上的一个向量空间,A是一个非空集合。对任何元素p∈A及向量a∈V,可定义加法p+a∈A,它满足条件:(1)p+ 0 =p,(2)(p+a)+b=p+ (a+b),(3)对任何q∈A,存在唯一的向量a∈V,使得q=p+a,这里a、b∈V。称A是一个“仿射空间”,K为其系数域。在仿射空间中,选定仿射标架后,空间中每一点就能用一个n-数组作为其坐标来表出。
分比 亦称“单比”。由仿射直线上的三个点所确定的一个数量。如A、B、C是仿射直线上的三点,则由点A、B所确定的向量 AB 及由点A、C所确定的向量 AC 成比例,于是有 AC =λ AB ,称λ为由A、B、C三点所确定的分比,记为(A,B,C)。
埃尔兰根纲领 德国数学家克莱因1872 年在埃尔兰根大学所提出的一种按照群论的观点来给几何学分类的思想。在此观点下,每种几何学都是研究在某种群的作用下不变的性质。例如,欧氏几何是研究在运动群下不变的性质,仿射几何是研究在仿射变换群下不变的性质,射影几何是研究在射影变换群下不变的性质。埃尔兰根纲领对几何学的发展产生了重大的影响。
曲线 在平面上或空间中按一定条件随时间(或另外的单个参数)而变动的动点的轨迹。例如,平面上一动点到一定点的距离保持不变的轨迹是圆。曲线按照它位于平面上或空间中分别称为“平面曲线”或“空间曲线”。
割线 和一条曲线有两个或两个以上交点的直线。
切线 过曲线C上的点P及另一点Q的割线l,当点Q沿曲线无限地趋近于点P时,如果直线l趋于一条定直线t,则称此定直线t为曲线C在点P的“切线”,称点P为“切点”。通过曲面上的一点,作曲面上的曲线,此曲线在这一点如有切线,则称此切线是曲面在这一点的一条切线。
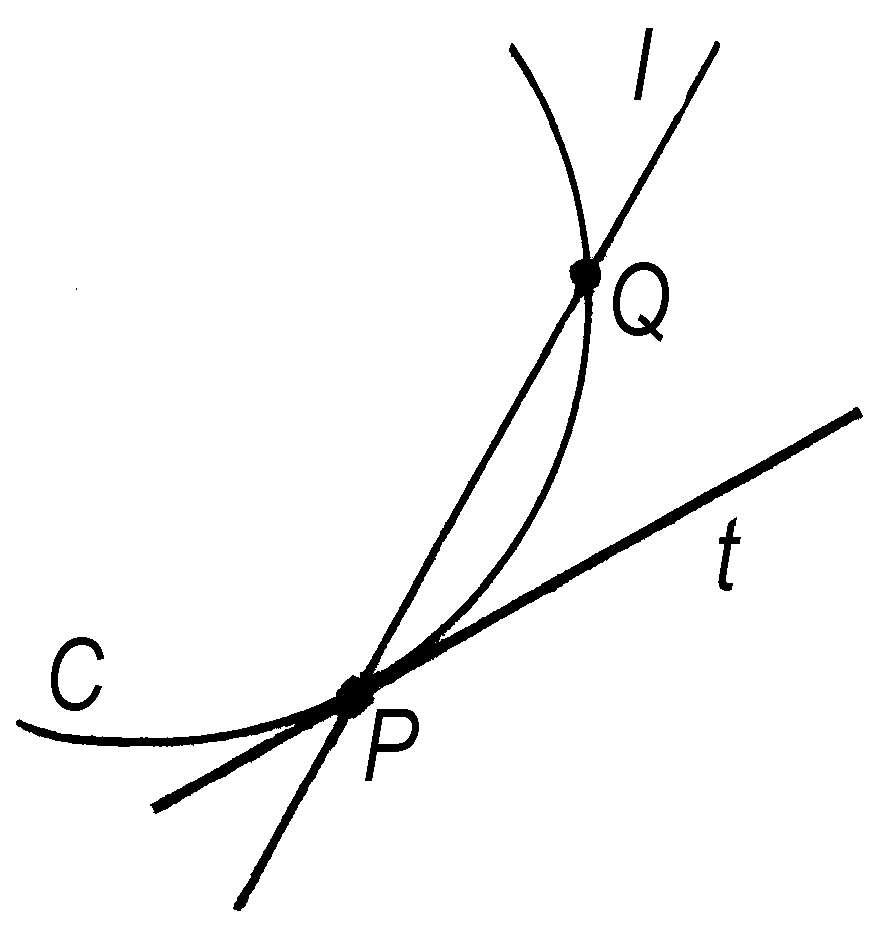
切 线
切点 见“切线”(97 页)。
公切线 当一直线切于两条或两条以上的曲线时,称此直线为这些曲线的“公切线”。例如,两个互不包含且互不相交的圆有四条公切线(如图):AB、CD称为“外公切线”;EF、GH称为“内公切线”。
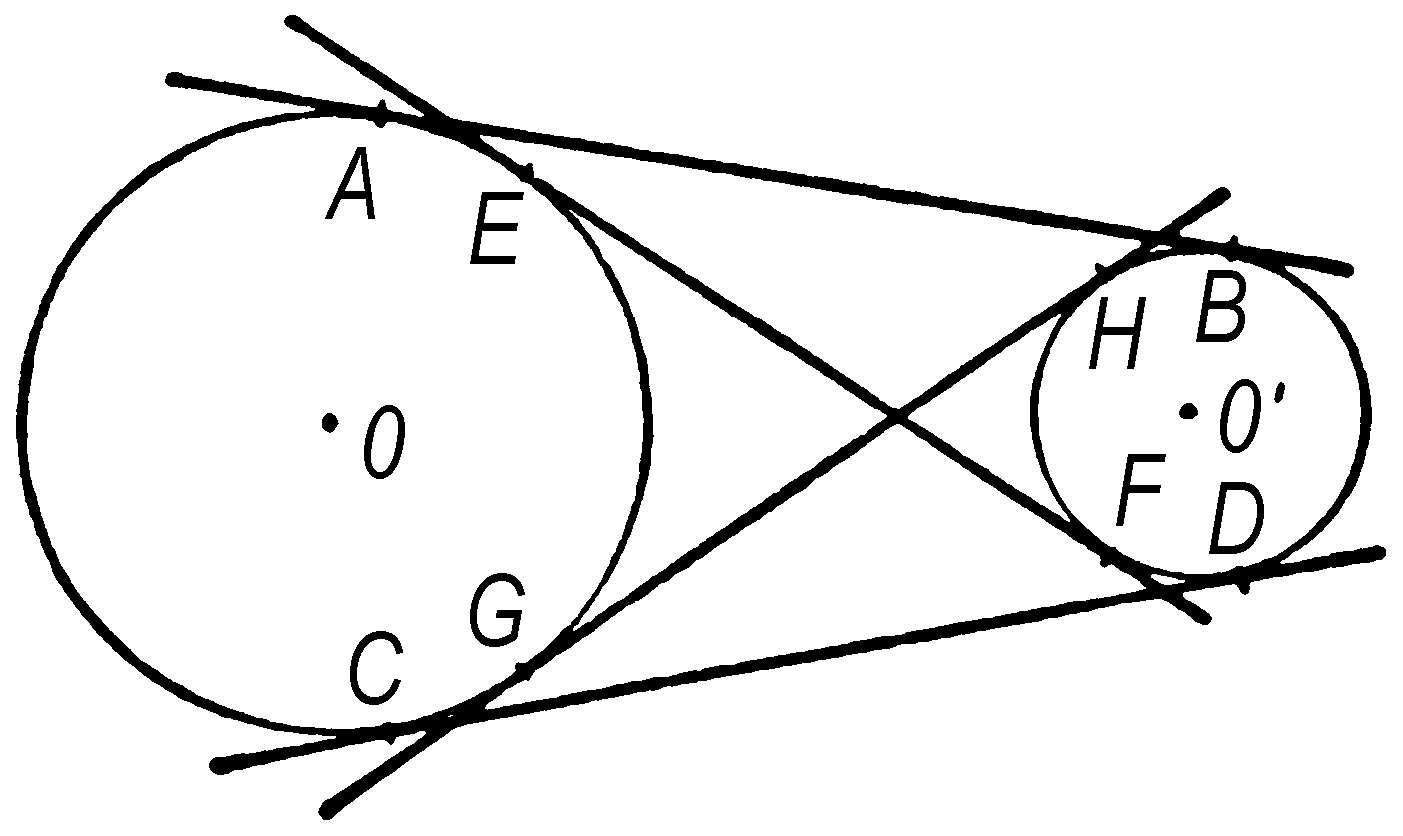
公切线
法线 过曲线上一点而且和曲线在这一点的切线垂直的直线,或过曲面上一点而且和曲面在这一点的切平面垂直的直线。
斜率 表示一条直线对横坐标轴倾斜程度的量。通常用直线和横坐标轴的交角的正切来表示。
曲率 描述曲线弯曲程度的量。对于曲线上的一点P,取它的两个邻近点Q和R,过这三点作一个圆。当Q、R沿曲线接近于P时,如果这个圆有一个极限位置,则称这个极限圆为曲线在点P的“曲率圆”,它的中心称为“曲率中心”,半径称为“曲率半径”,曲率半径的倒数称为“曲率”。曲率愈大,表示曲线的弯曲程度愈大。
挠率 描述空间曲线在其每点的邻近处偏离其密切平面程度的一种量度。挠率处处为零的曲线即为平面曲线。
包络 一曲线在它的每一点常和一族曲线中的一条相切,则这曲线称为这族曲线的“包络”。例如,圆心在一直线上而半径相等的圆族的包络是两条平行直线。对曲面族也可类似地定义其包络面。
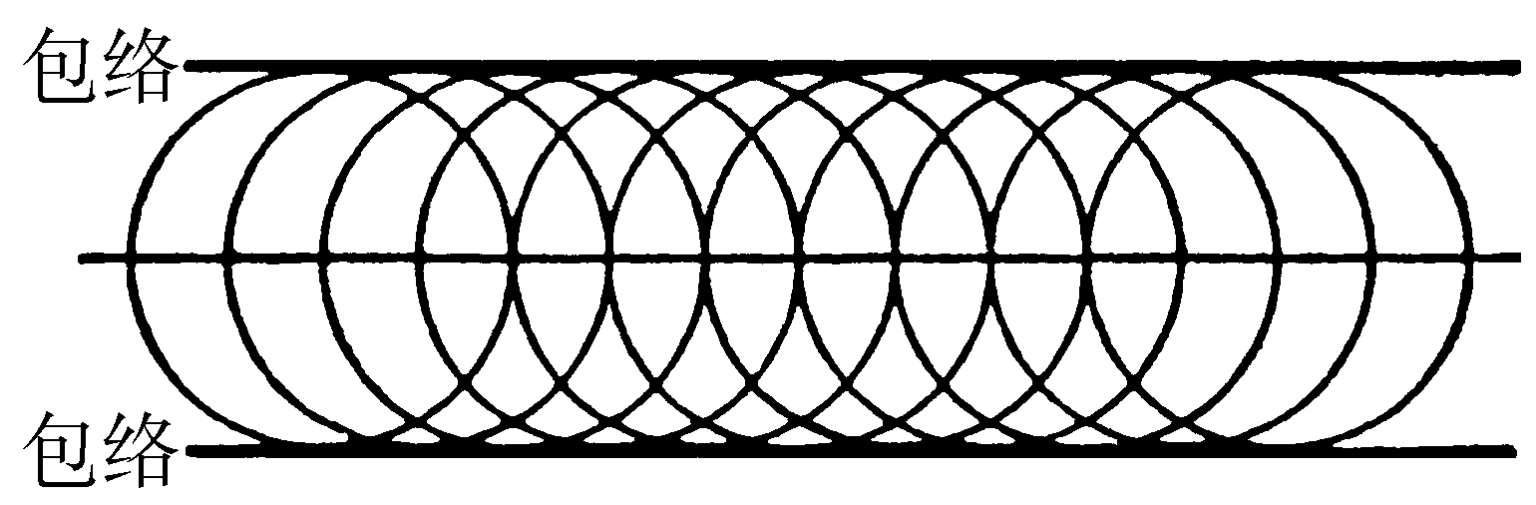
包 络
渐屈线 当一条曲线在各点的法线成为另一条曲线的切线时,称后一条曲线为原曲线的“渐屈线”;而称原曲线为后一条曲线的“渐伸线”或“渐开线”。一条平面曲线至多只有一条渐屈线,但是,有无限条渐伸线。
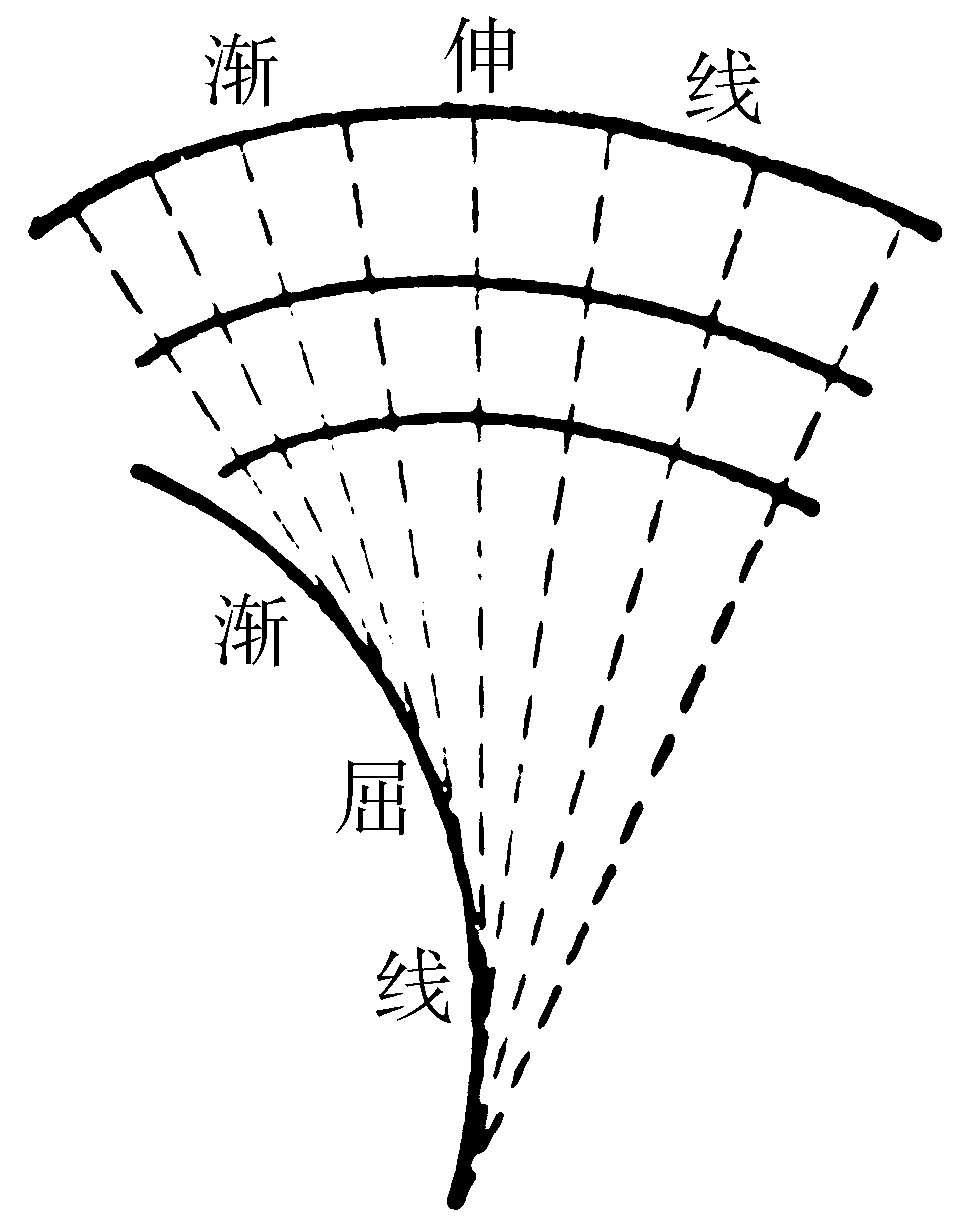
渐屈线
渐伸线 亦称“渐开线”。一直线在一个圆上作无滑动的滚动时,直线上一定点运动的轨迹为“圆的渐开线”。机械制造中,常用渐开线作齿轮的齿廓曲线。详见“渐屈线”。
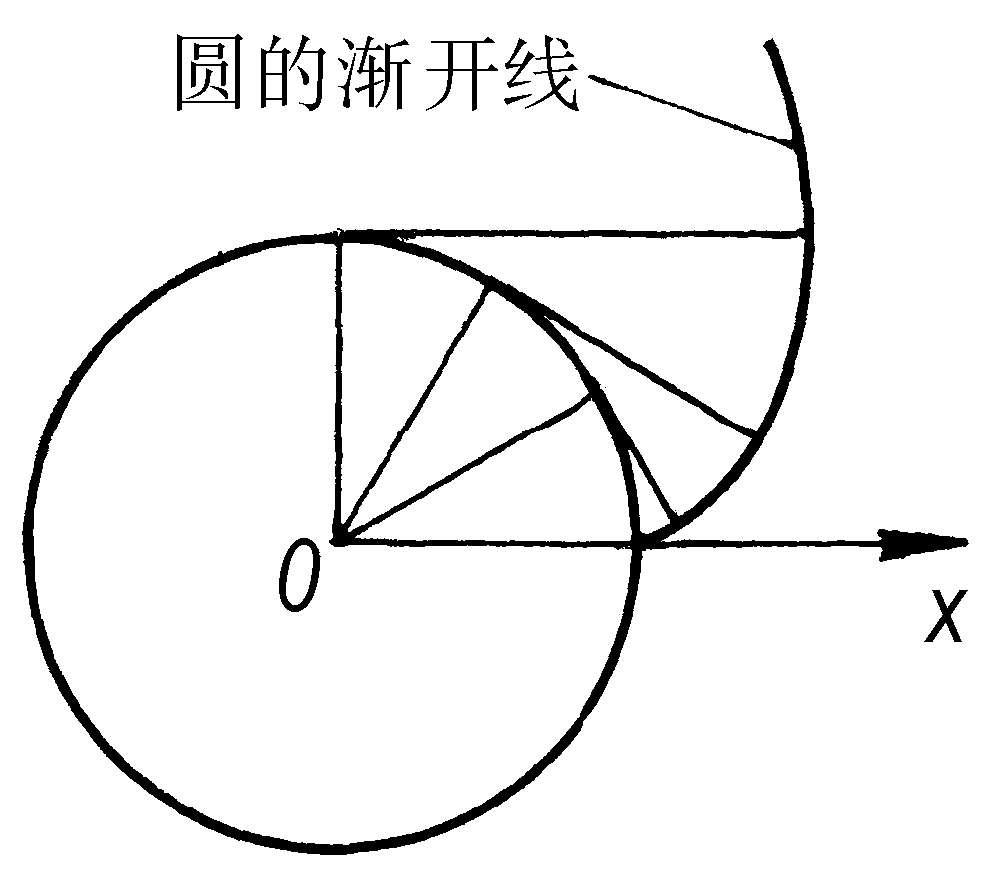
渐伸线
圆的渐开线 见“渐伸线”。
渐近线 当无限伸展的一条曲线上一个动点沿曲线移向无限远时,如果它和一条定直线的距离趋向于零,则称此直线为曲线的“渐近线”。例如,双曲线x 2 -y 2 = 1 有两条渐近线:x-y= 0 和x+y= 0。
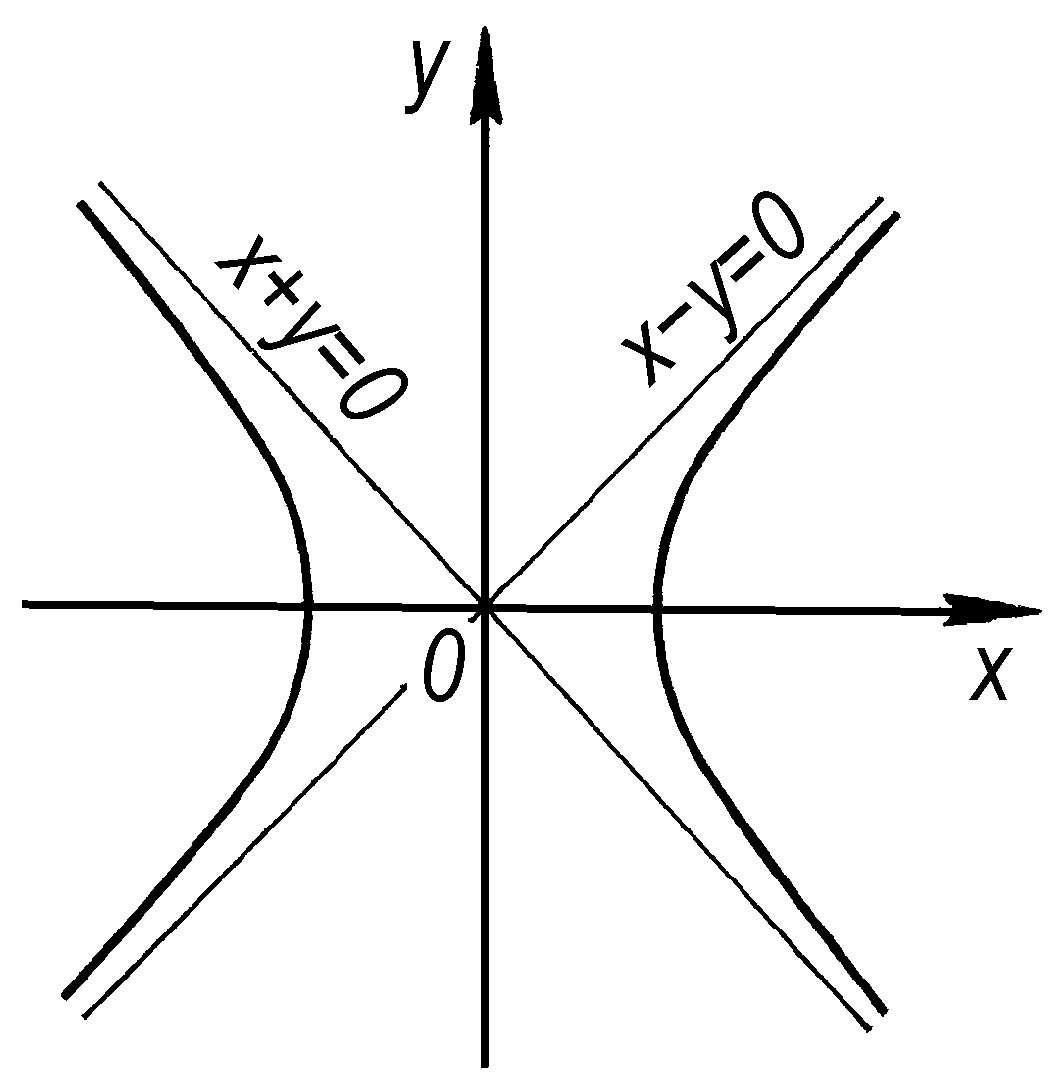
渐近线
卵形线 亦称“凸闭曲线”。它是一条闭曲线,且曲线上任意两点的连接线段全部包含在由此闭曲线所围成的区域之中。
圆锥曲线 从顶点向两侧伸长的两叶圆锥面和任一平面相交而成的曲线。当截面不过顶点时,曲线是椭圆、双曲线或抛物线。当截面过顶点时,曲线退缩为一点或一对直线(相交、平行或重合)。在平面直角坐标系下,这些曲线的方程是x、y的二次方程,故亦称“二次曲线”。
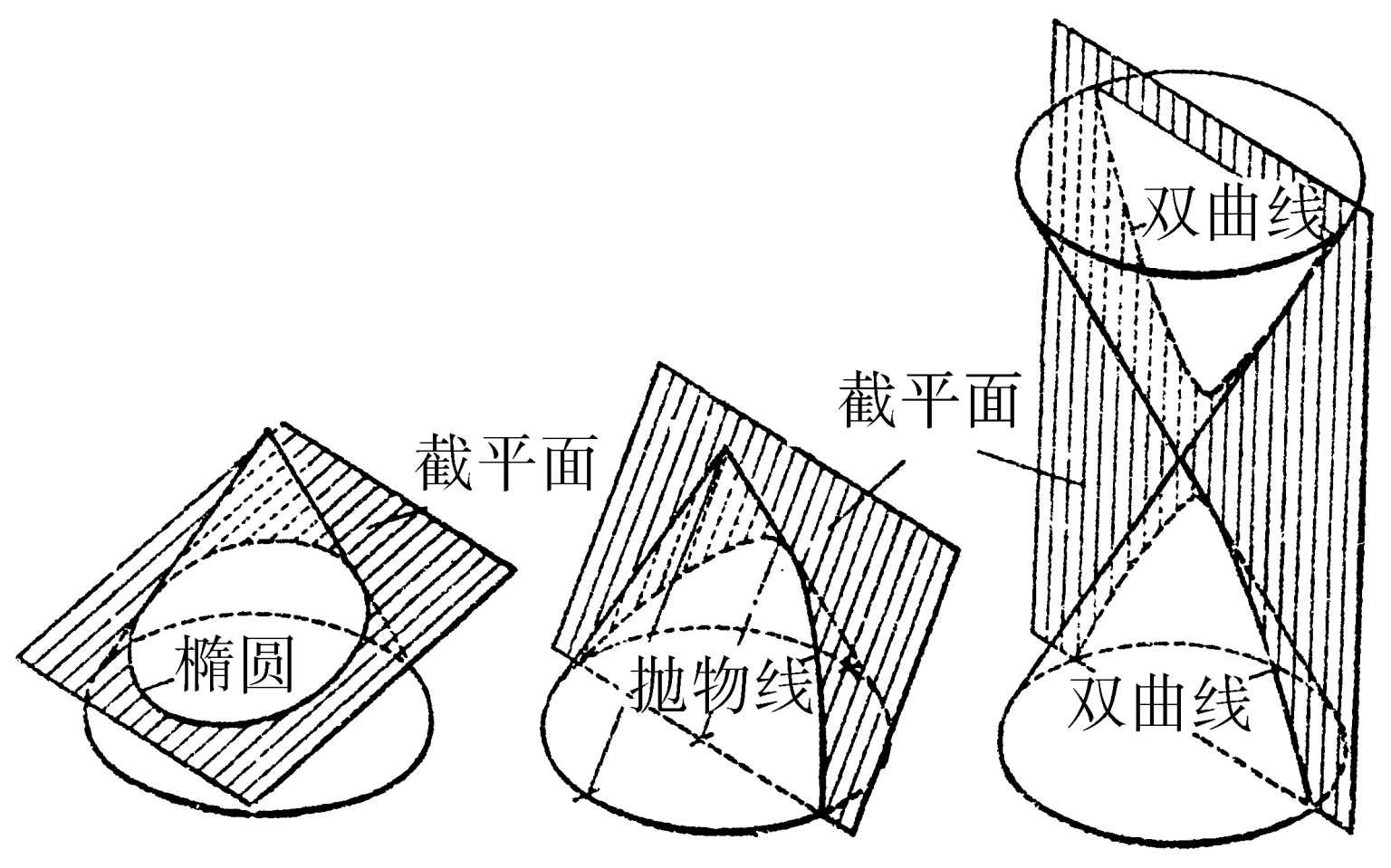
圆锥曲线
二次曲线 即“圆锥曲线”。
椭圆
圆锥曲线的一种。当平面上动点P到两定点F、F′的距离的和是常数时,点P的轨迹称为“椭圆”,F、F′称为焦点。对焦点F(或F′)有直线d(或d′)使椭圆上的点P到F(F′)和它到直线d(d′)的距离之比e恒为小于 1 的常数。称直线d和d′为“准线”,e为“离心率”。在直角坐标系下,椭圆的标准方程为
 。当a=b时,它成为圆。
。当a=b时,它成为圆。
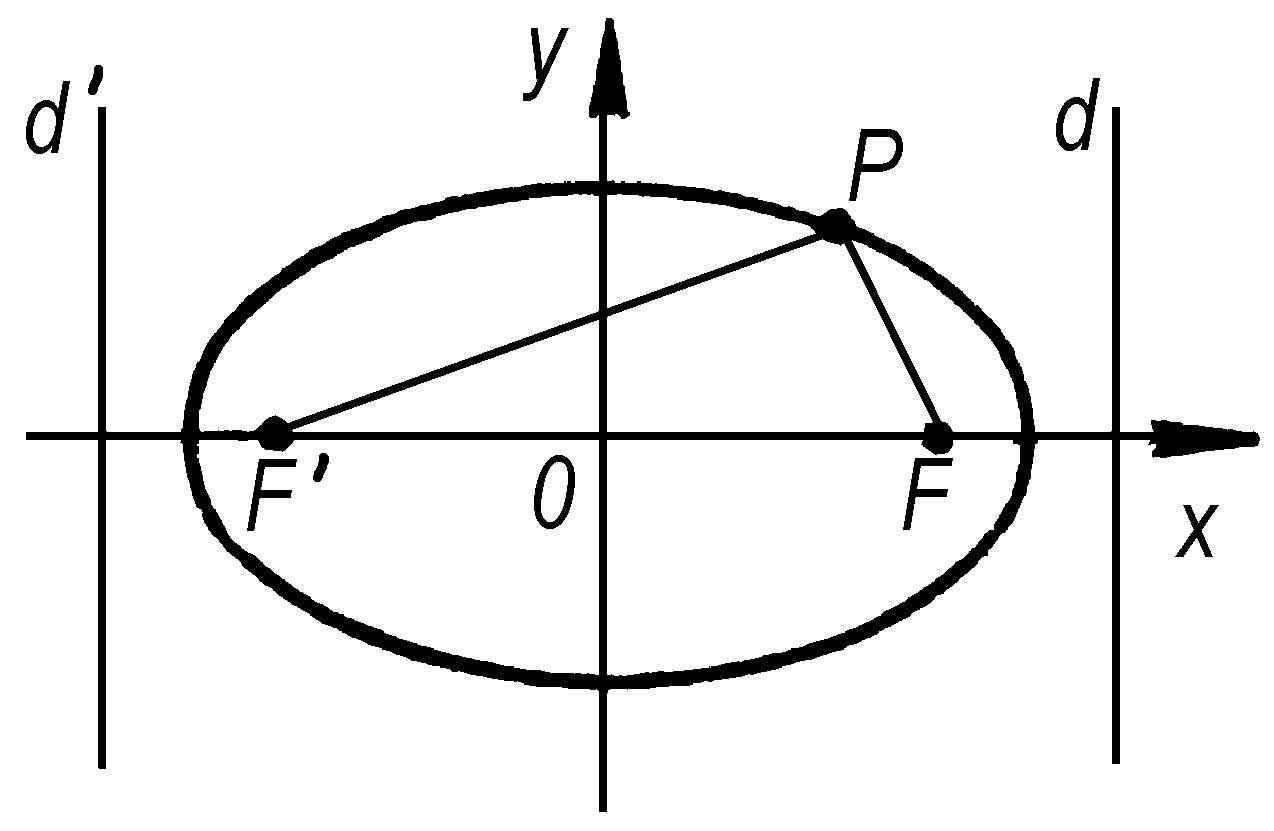
椭 圆
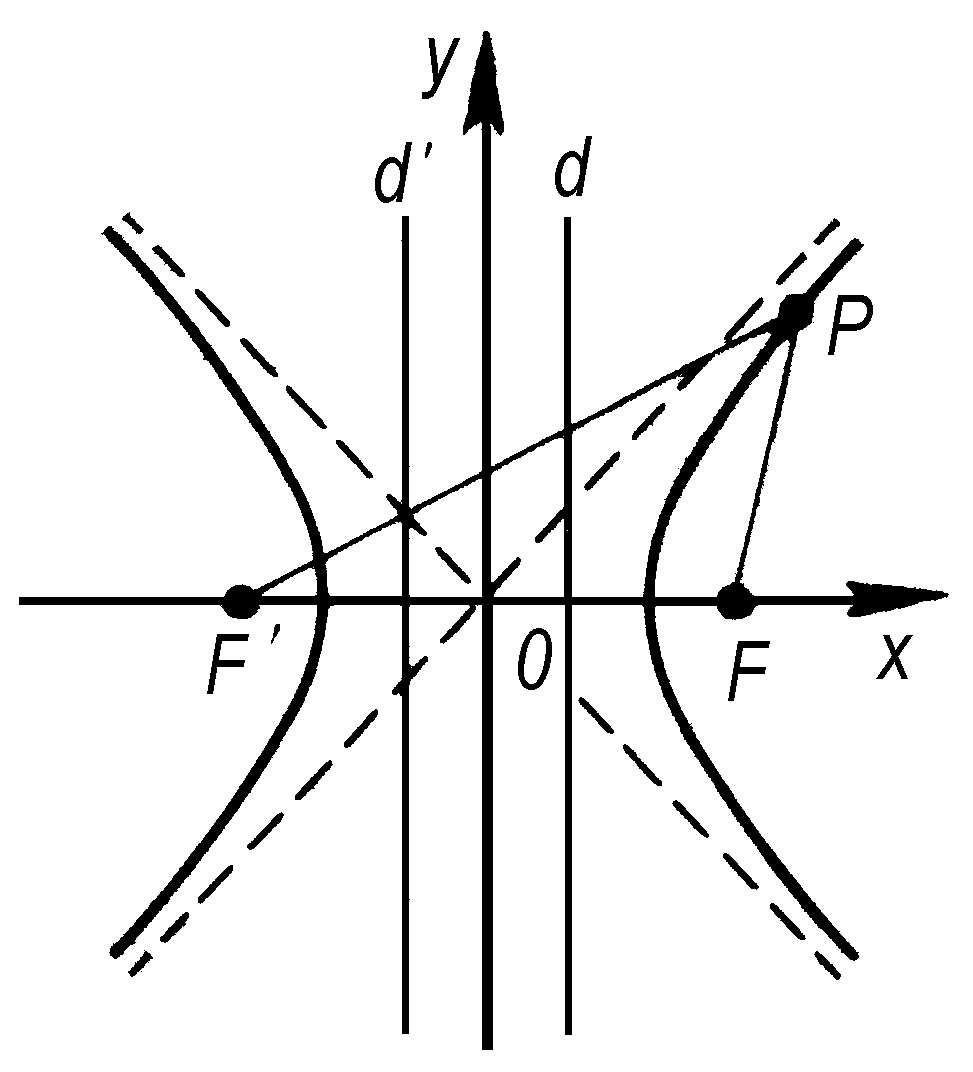
双曲线
圆锥曲线的一种。当平面上动点P到两定点F、F′的距离之差是常数时,点P的轨迹称为“双曲线”,F、F′称为焦点。对焦点F(或F′)有直线d(或d′)使双曲线上点P到F(F′)和它到直线d(d′)的距离之比e恒为大于 1 的常数。称直线d和d′为“准线”,e为“离心率”。在直角坐标系下,双曲线的标准方程为
 当a=b时,称为等轴双曲线。
当a=b时,称为等轴双曲线。
双曲线
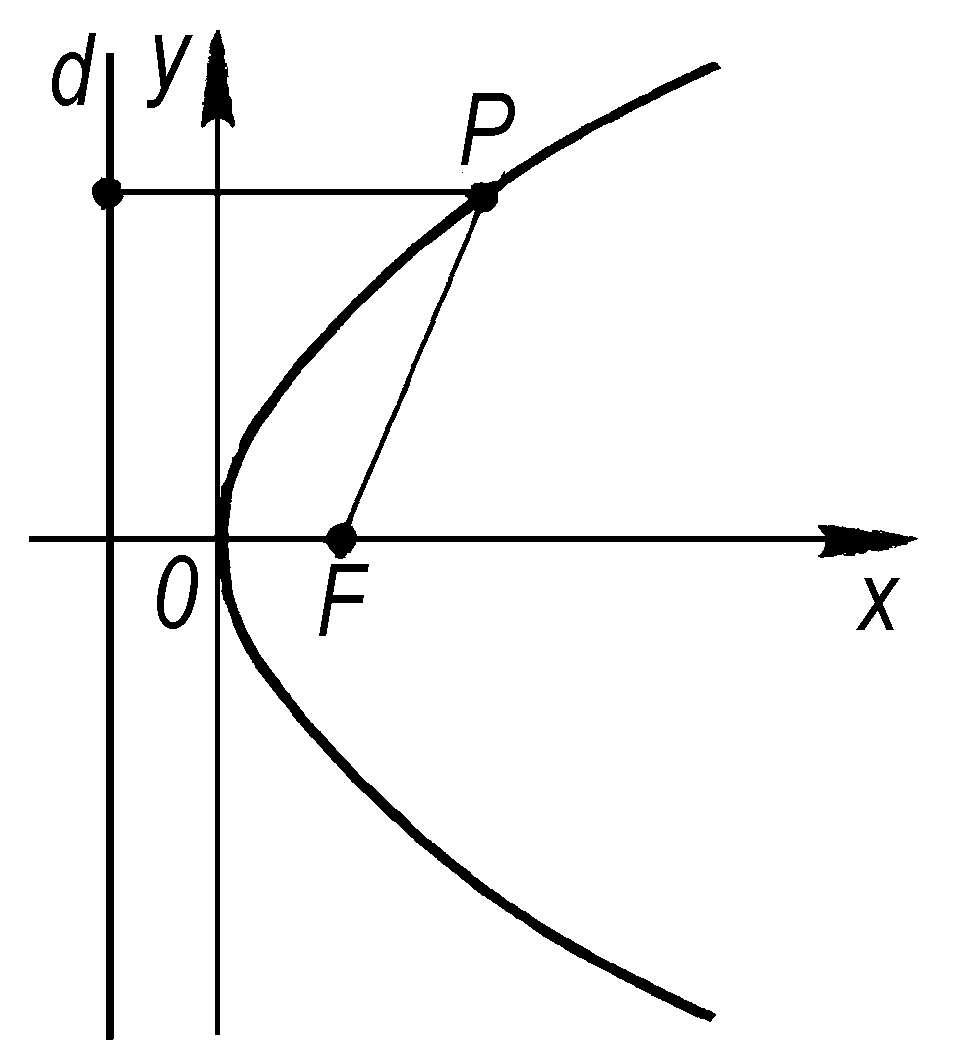
抛物线 圆锥曲线的一种。当平面上动点P到定点F和到定直线d的距离相等时,点P的轨迹称为抛物线。F为“焦点”,d为“准线”,过F引d的垂直线是抛物线的对称轴。在直角坐标系下,抛物线的标准方程是y 2 = 2px,式中p是正数。
抛物线
离心率 当动点P到一定点的距离和到一定直线的距离之比恒等于常数e时,按照e小于、等于和大于 1,P的轨迹分别是椭圆、抛物线和双曲线,称e为这些轨迹的“离心率”,定点为“焦点”,定直线为“准线”。
准线 见“离心率”。
焦点 见“离心率”。
直径 圆锥曲线的一族平行弦的中点的轨迹是一条直线,称为“直径”。圆和椭圆的直径是过中心的弦。
主轴 当圆锥曲线的一条直径的任一垂直弦为这直径所平分时,称这直径为“主轴”或“主直径”。圆锥曲线的主轴就是它的对称轴。
代数曲线 在直角坐标系中,如果点(x,y)满足一个二元既约代数方程F(x,y)= 0,则称这点的轨迹为“代数曲线”。这既约多项式F(x,y)的次数称为代数曲线的次数。例如,直线是一次的,椭圆、双曲线、抛物线都是二次的。
悬链线 对于直角坐标,称方程
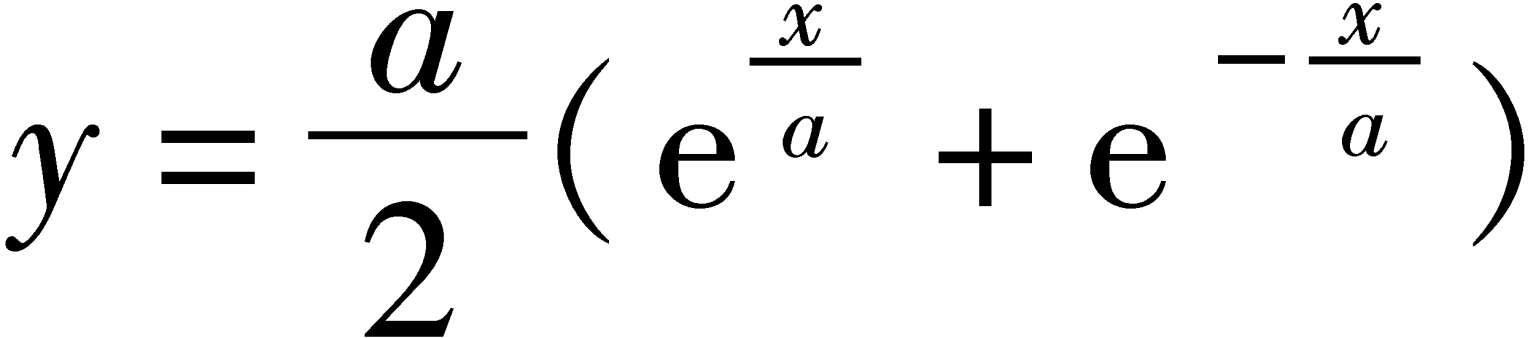
悬链线
所确定的曲线为“悬链线”。在两个固定点间挂一链条,它在重力作用下,大致下垂成悬链线的形状。
摆线 当一个圆在定直线上滚动时,圆周上定点P的轨迹称为“摆线”,亦称“旋轮线”(图 1)。当一质点仅凭重力从P降到M时,以沿如图 2 的摆线下降为最速,
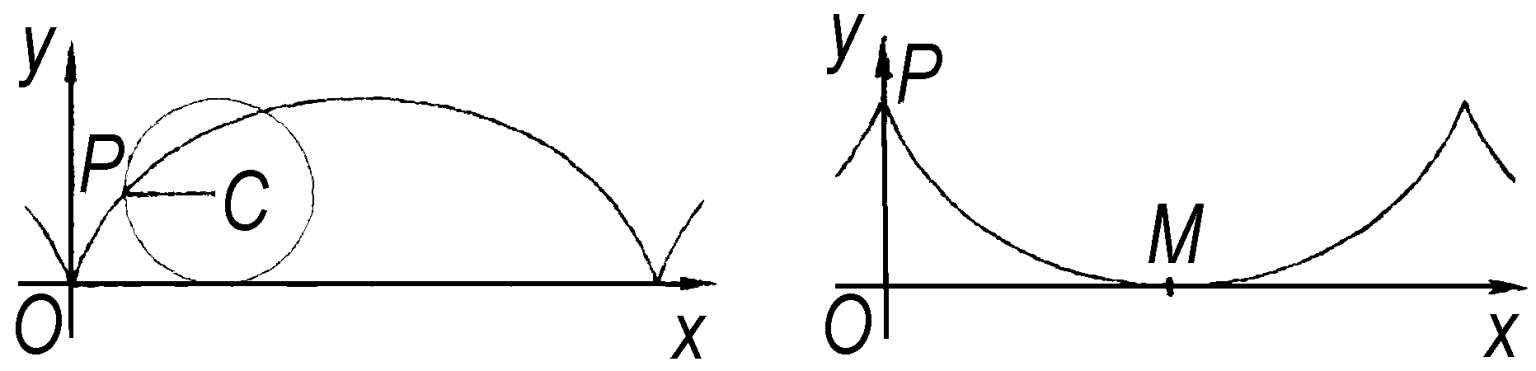
(1)旋轮线(2)最速降线
所以又称摆线为“最速降线”或“捷线”。当动圆在另一圆的内部或外部滚动时,动圆周上定点P的轨迹分别称为“内摆线”(图 3)和“外摆线”(图 4)。在机械工业上,内外摆线有时被采用为齿轮齿廓曲线的一部分。
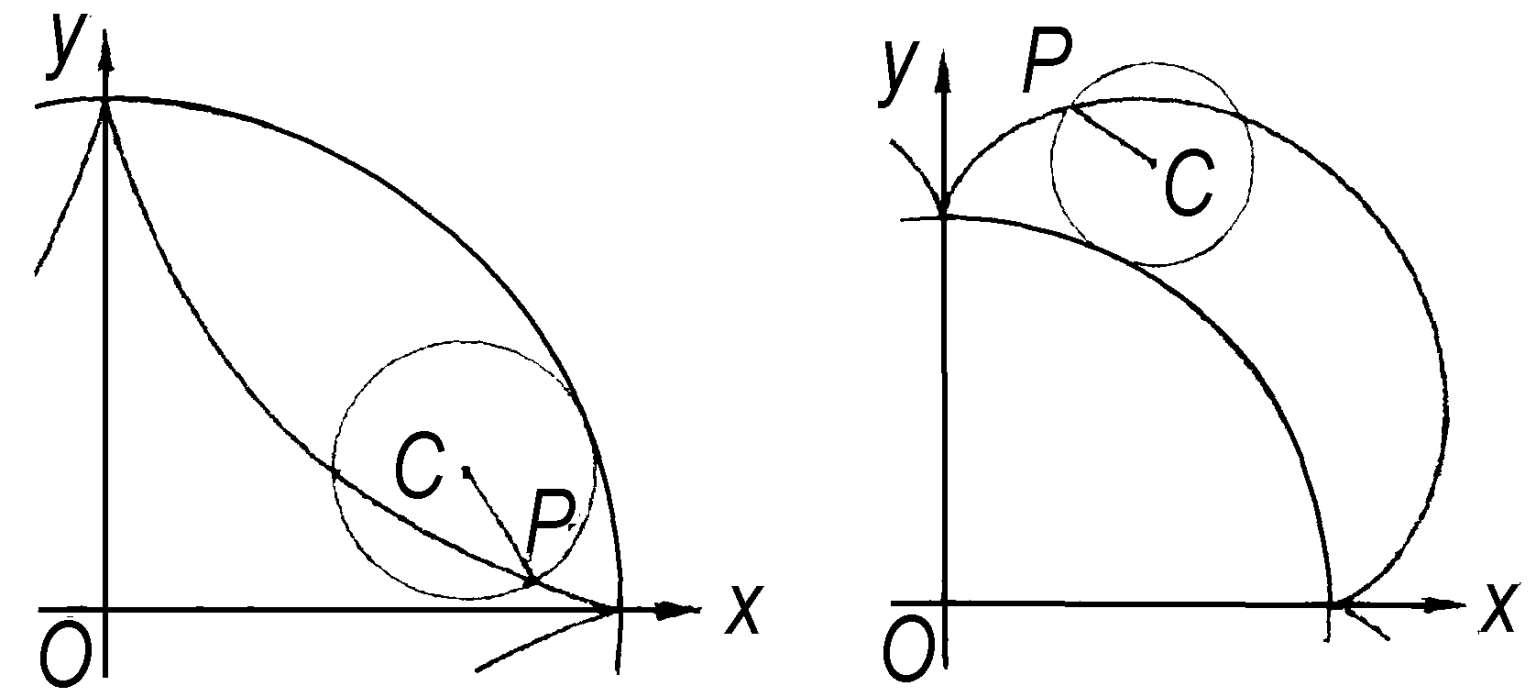
(3)内摆线(4)外摆线
旋轮线 见“摆线”。
最速降线 见“摆线”。
螺线 围绕一中心点或轴旋转,同时又逐渐远离的动点轨迹。设(r,θ)是点P的极坐标。当矢径r随极角θ的增加而增加(或减小)时,点P(r,θ)的轨迹是一螺线。例如,r=aθ是阿基米德螺线,其中a是常数。在机械工业上,常用阿基米德螺线作为凸轮的轮廓曲线。
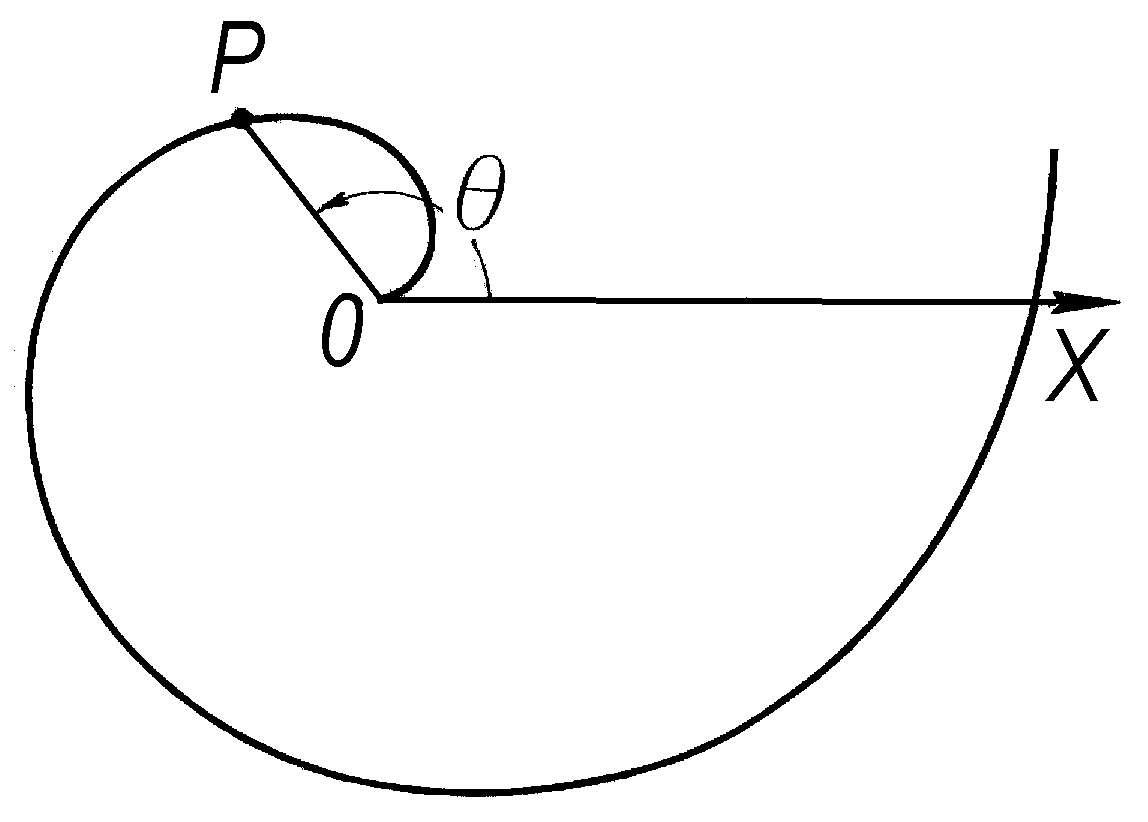
阿基米德螺线
阿基米德螺线 亦称“等速螺线”。见“螺线”。
等速螺线 即“阿基米德螺线”。
玫瑰线
极坐标方程r=acosnθ或r=asinnθ(0≤θ< 2
 )所表示的平面曲线。如,r=asin3θ有三叶,r=acos2θ有四叶。
)所表示的平面曲线。如,r=asin3θ有三叶,r=acos2θ有四叶。
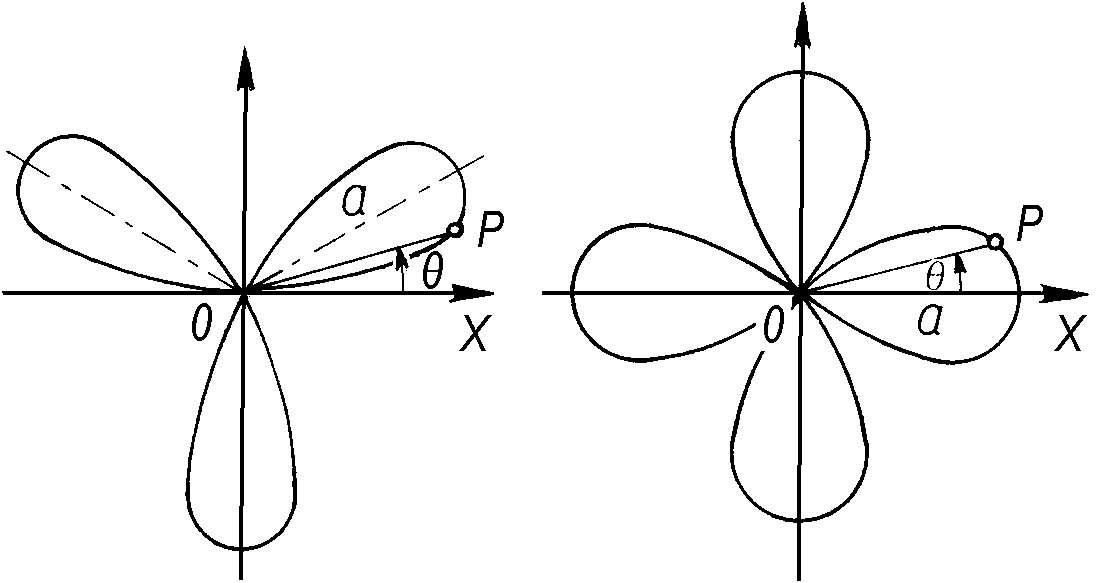
玫瑰线
曳物线 重物置于一直道之外,人用绳拖此重物并沿直道向前走时重物所经过的轨迹线。将此曳物线绕直道为轴旋转一周后所形成的曲面称为“伪球面”。罗巴切夫斯基等所发现的非欧几何学可以局部地在伪球面上实现。
曳物线
伪球面
伪球面 见“曳物线”。
曲面 当空间一点的直角坐标(x,y,z)满足方程f(x,y,z)= 0 时,这点的轨迹是曲面,但f(x,y,z)要满足一些补充条件。例如,空间中与一定点等距离的点的轨迹是球面,与一定直线等距离的点的轨迹是圆柱面。
切平面 当曲面上经过一点的切线的全体构成一个平面时,称这个平面为曲面在这一点的“切平面”。
直纹面 空间中一动直线所画成的曲面。直线称为“母线”。例如柱面、锥面、单叶双曲面等。
母线 见“直纹面”。
柱面 直纹面的一种。过定曲线上一个动点而与某一条定直线平行的动直线所构成的曲面。动直线是柱面的母线。当定曲线是圆周,且定直线垂直于圆周所在平面时,称所得的柱面为“正圆柱面”或“圆柱面”。
圆柱面 亦称“正圆柱面”。见“柱面”。
圆柱 以矩形的一边所在的直线为旋转轴,其余各边旋转一周所得到的几何体。称平面部分为“底面”,曲面部分为“侧面”,底面间的距离称“高”。当两底面中心的连线垂直于底面时,称“正圆柱”。正圆柱的侧面积等于底的周长乘高,体积等于底面积乘高。
锥面 直纹面的一种。平面曲线上一动点与平面外一定点的连线所构成的曲面。定点称为“顶点”,活动的连线称为“母线”。
立体角 一个锥面所围成的空间部分。是以锥的顶点为球心、半径为 1 的球面被锥面所截得的面积来度量的,度量单位称为“球面度”,符号sr。
圆锥面 圆周上动点与圆所在平面外一定点的连线所构成的曲面。定点称为“顶点”。一个平面与圆锥面所围成的立体称为“圆锥”;平面部分是它的底面,锥面部分是它的侧面,圆锥的顶点到底面的距离是它的高。圆锥的体积等于它的底面积乘高的三分之一。当顶点到底面圆心的连线垂直于底面时,圆锥称为“正圆锥”,连线称为轴。
圆锥面
圆锥 见“圆锥面”。
圆台 正圆锥被两个垂直于轴的平面所截的部分。截面称为“底面”,底面间的距离称为“高”。设S 1 和S 2 为圆台两底的面积,h为它的高,则其体积是:
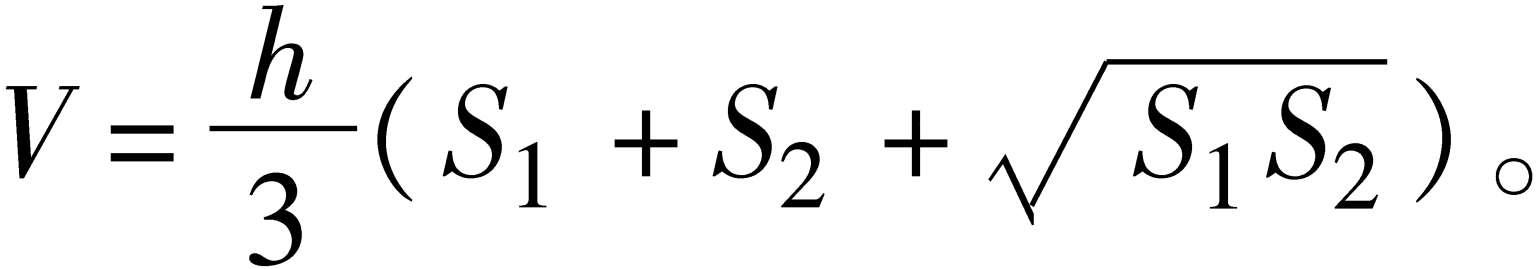
球面
空间中与定点有定距离的动点的轨迹。称定点为“球心”,定距离为“半径”。球面所围成的立体称为“球体”,有时也简称“球”。半径为R的球的面积是
 ,体积是
,体积是

大圆 球面被通过球心的平面所截得的圆。
球面角 球面上两个大圆所夹的角,用两个大圆在交点的切线的交角来度量。
球面多边形
亦称“球面多角形”。球面上由若干大圆弧所围成的图形。构成图形的各大圆弧的弧称为“球面多边形的边”,相邻两大圆弧所成的球面角称为“球面多边形的内角”,同一大圆弧上球面多边形的内角的邻角称为“球面多边形的外角”。球面多边形的各外角之和小于 2
 弧度。设球半径为r,球面多边形的各外角的弧度值为
弧度。设球半径为r,球面多边形的各外角的弧度值为

 ,则n边球面多边形的面积
,则n边球面多边形的面积
 。
。
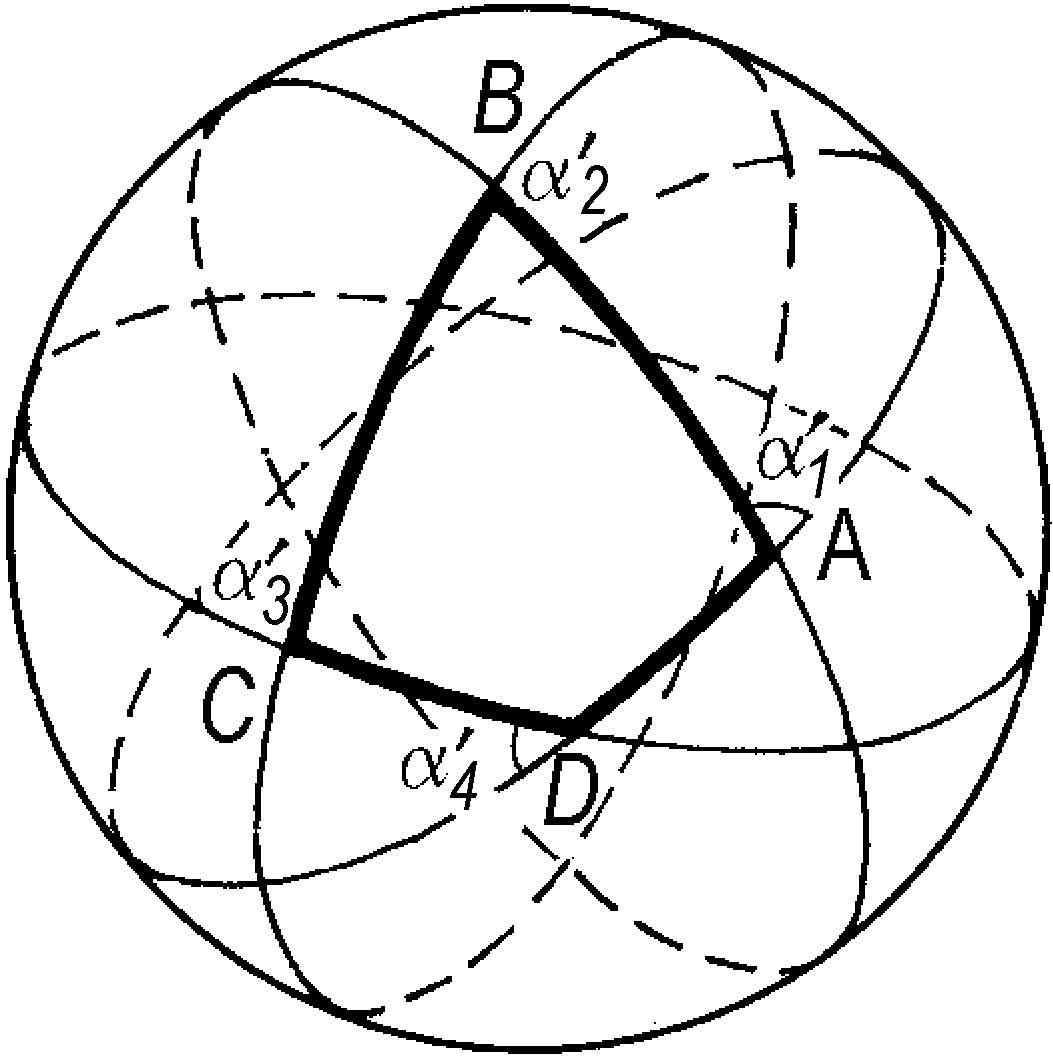
球面多边形
球冠 球面被一个平面截得的部分。截面圆称为“球冠的底”,垂直于截面的直径在截面和球面之间的线段长称为“球冠的高”。球冠也可看作是一段圆弧(一端在直径的一端上)绕着圆弧所在圆的直径旋转一周而得到的曲面。设球冠的高为h,球的半径为r,则球冠的面积
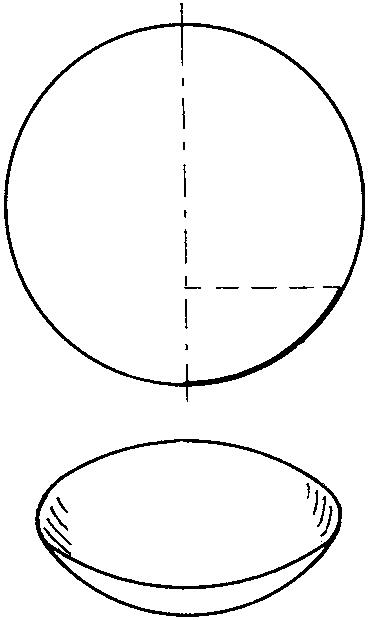
球 冠
球带 球面被两个平行平面所截,夹在此两平面间的球面部分。截得的两个平行的圆称为“球带的底”,两个平行平面间的距离称为“球带的高”。球带也可看作是一段圆弧(两端不在直径上)绕着圆弧所在的圆的直径旋转一周而得到的曲面。设球带的高为h,球的半径为r,则球带的面积
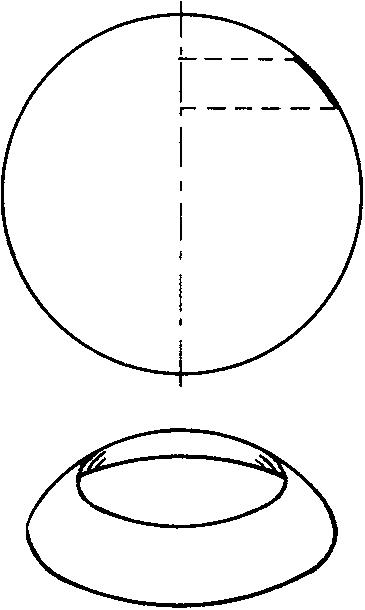
球 带
球缺 一个平面截球所得球的部分。垂直于截面的球的直径被此截面截得的线段称为“球缺的高”。球缺也可看作是半个弓形绕着弓形所在圆的直径旋转一周而得到的立体。设球缺的高为h,球的半径为r,则球缺的体积
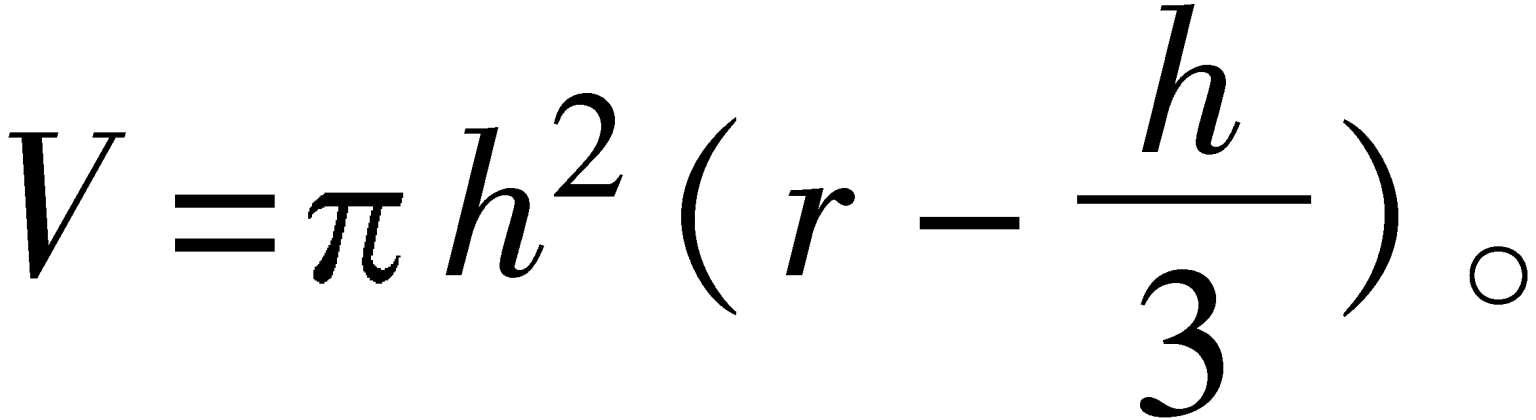
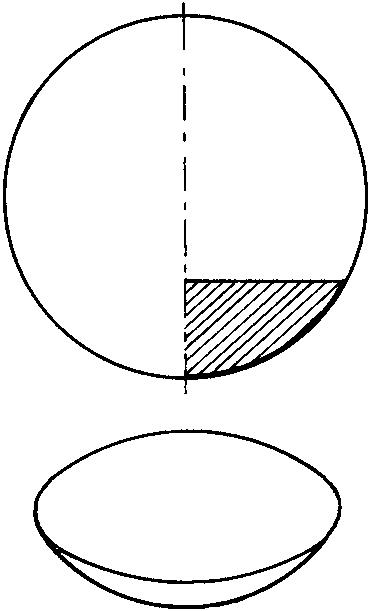
球 缺
球台 亦称“球盘”。两个平行平面截球,夹在此两平行平面间的球的部分。两个平行平面间的距离称为“球台的高”。球台也可看作是一个曲边梯形绕着它所在圆的直径旋转一周而得到的立体。设球台的高为h,上、下两底面圆的半径为a、b,球半径为r,则球台的体积
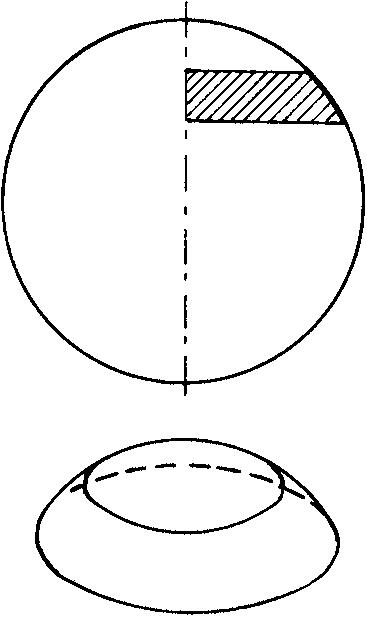
球 台
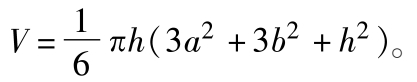
球扇形 亦称“球心角体”。以一条过扇形的圆心而不通过扇形内部且与扇形在同一平面内的直线为轴,将扇形旋转一周所得到的立体。有两种不同的形状(如图)。设球扇形底面(球冠或球带)的高为h,球半径为r,则球扇形的体积
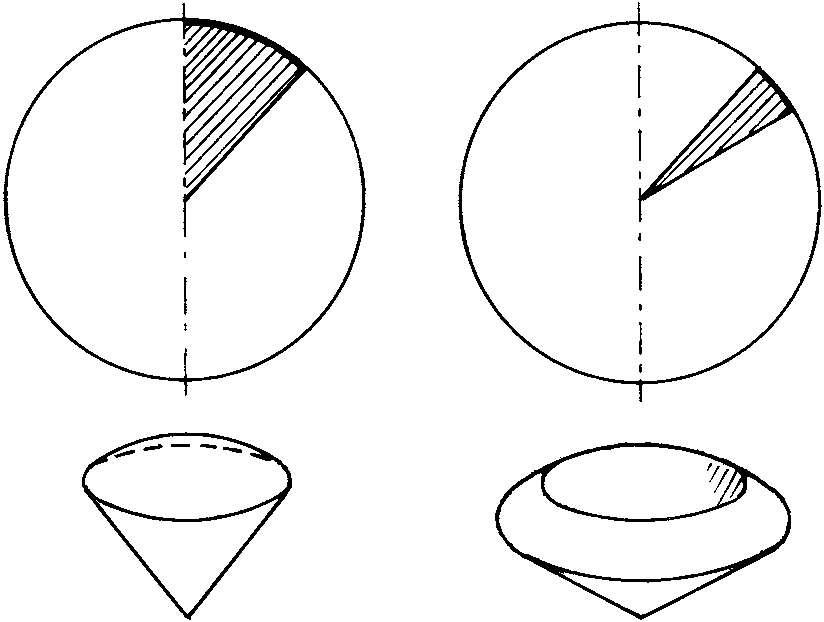
球扇形
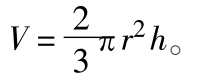
二次曲面 空间点坐标(x,y,z)的二次代数方程所表示的曲面。椭球面、双曲面、抛物面都是二次曲面。二次曲面可以退缩为锥面或一对平面。
椭球面
设(x,y,z)是直角坐标,则由标准形方程
 所表示的曲面称为“椭球面”。椭球面所围成的立体称为“椭球”。它与三坐标轴相截所得的三条线段,称为“轴”。椭球关于三坐标轴都是对称的。它与平面相交的截线是椭圆(如图)。
所表示的曲面称为“椭球面”。椭球面所围成的立体称为“椭球”。它与三坐标轴相截所得的三条线段,称为“轴”。椭球关于三坐标轴都是对称的。它与平面相交的截线是椭圆(如图)。
椭球面
椭球 见“椭球面”。
双曲面 二次曲面的一种,分单叶双曲面和双叶双曲面两类。
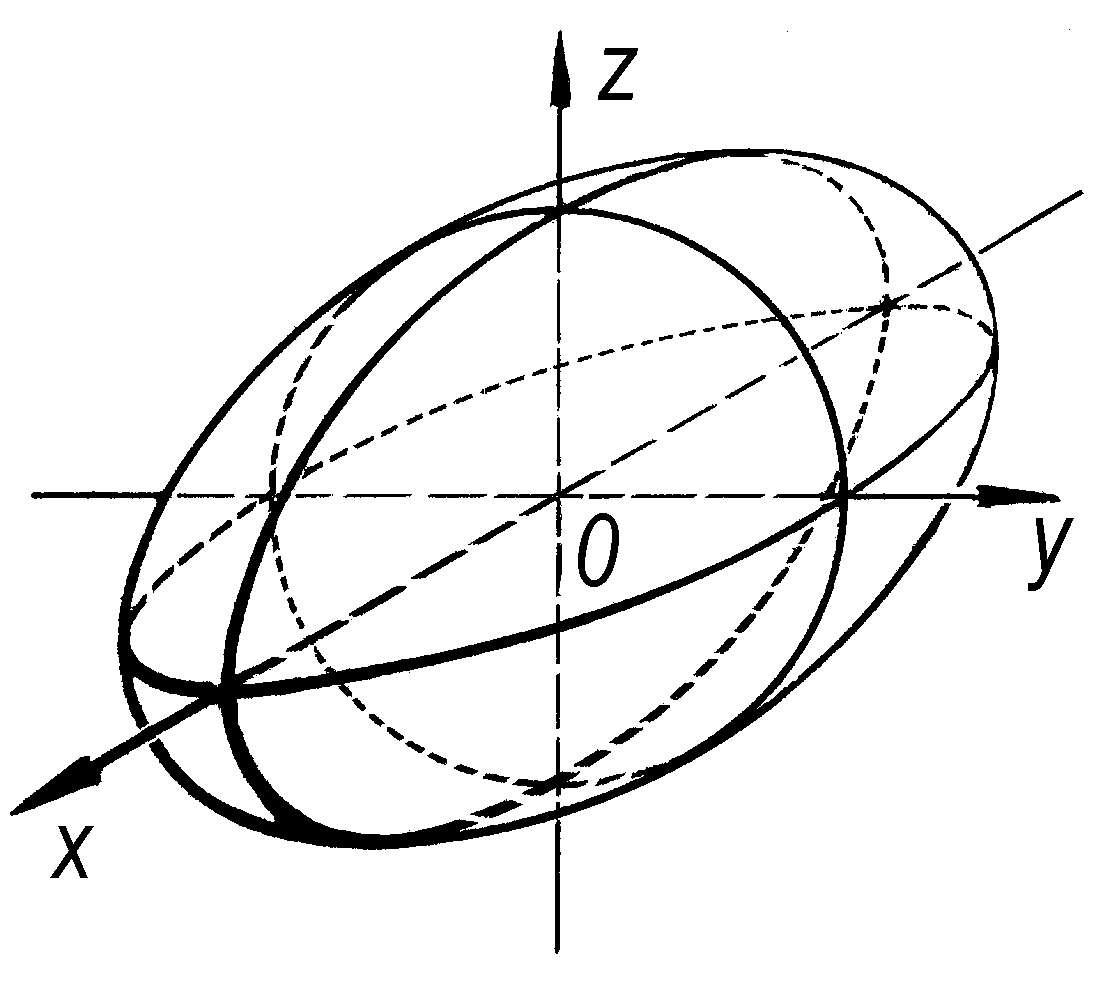
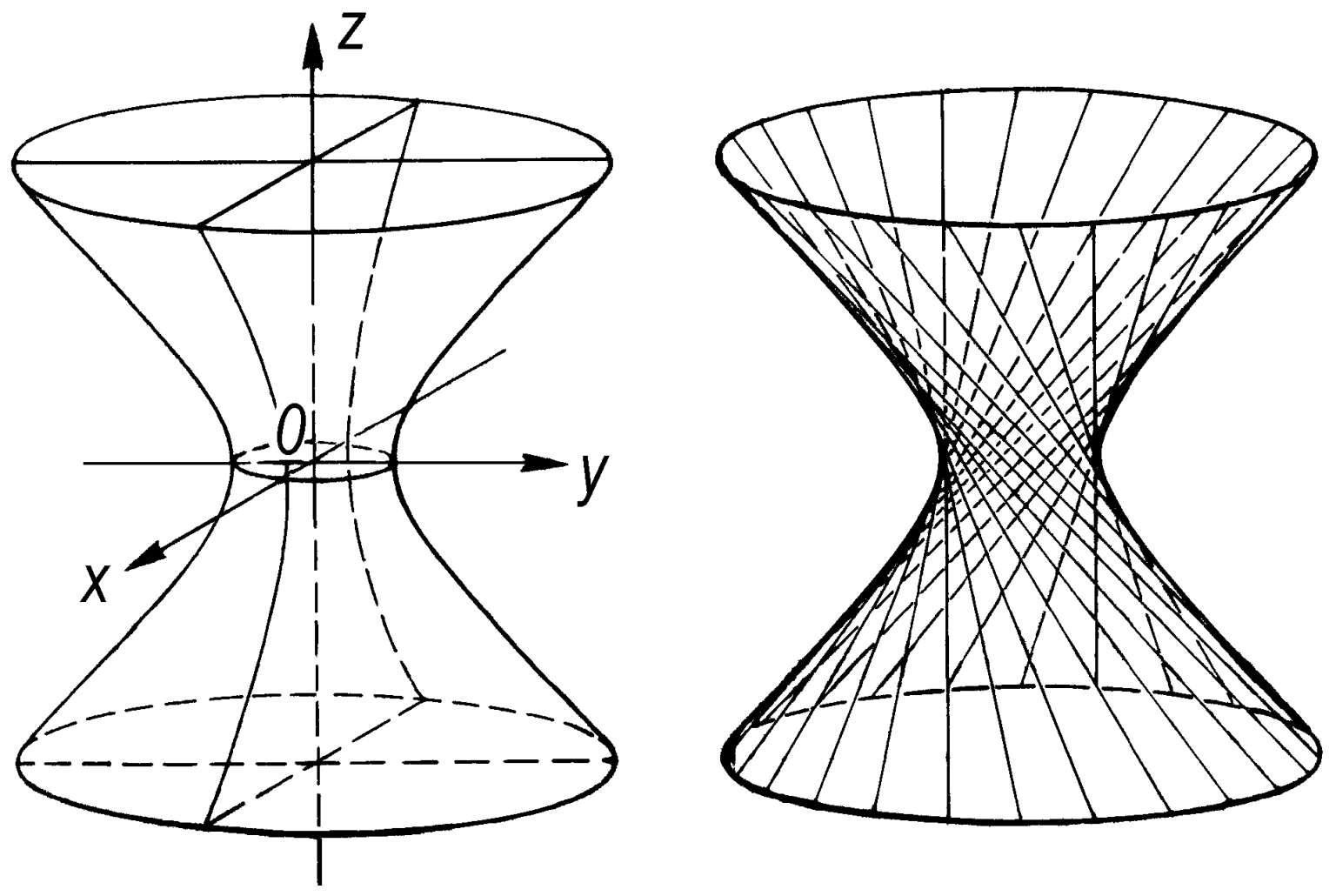
单叶双曲面 设(x,y,z)是直角坐标,则由标准形方程
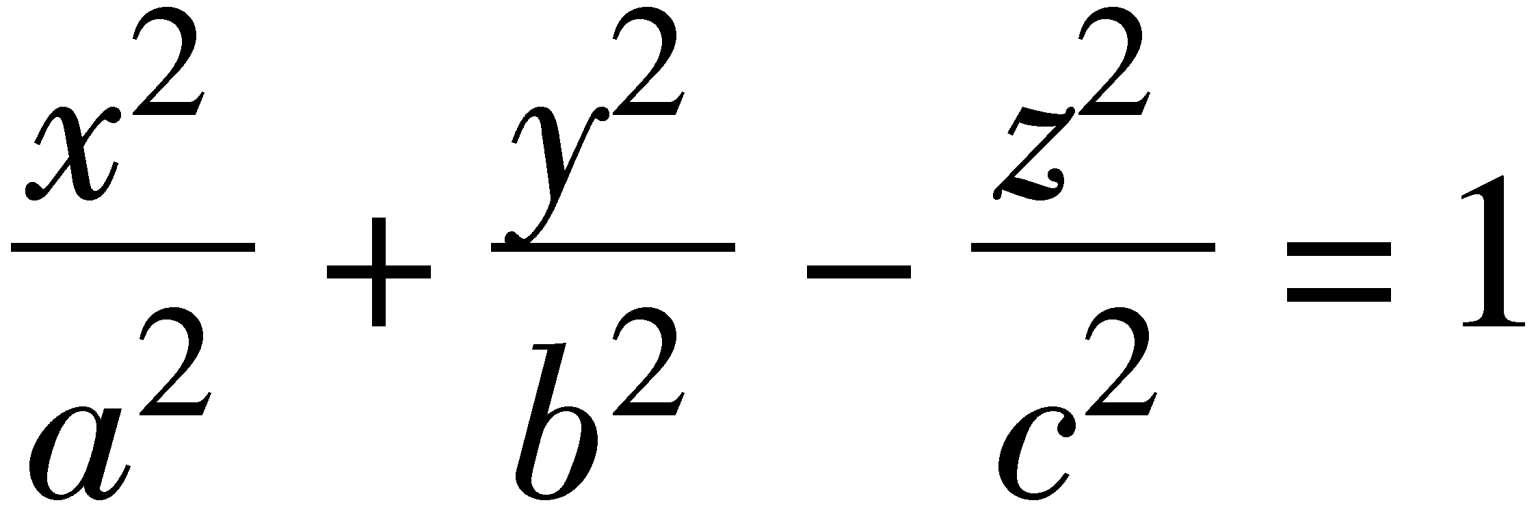
所表示的曲面称为“单叶双曲面”。它与平行于xOy平面的截线都是椭圆,与垂直于Ox轴或Oy轴的平面的截线都是双曲线。它是具有两组母线的直纹面。
单叶双曲面
双叶双曲面 设(x,y,z)是直角坐标,则由标准形方程
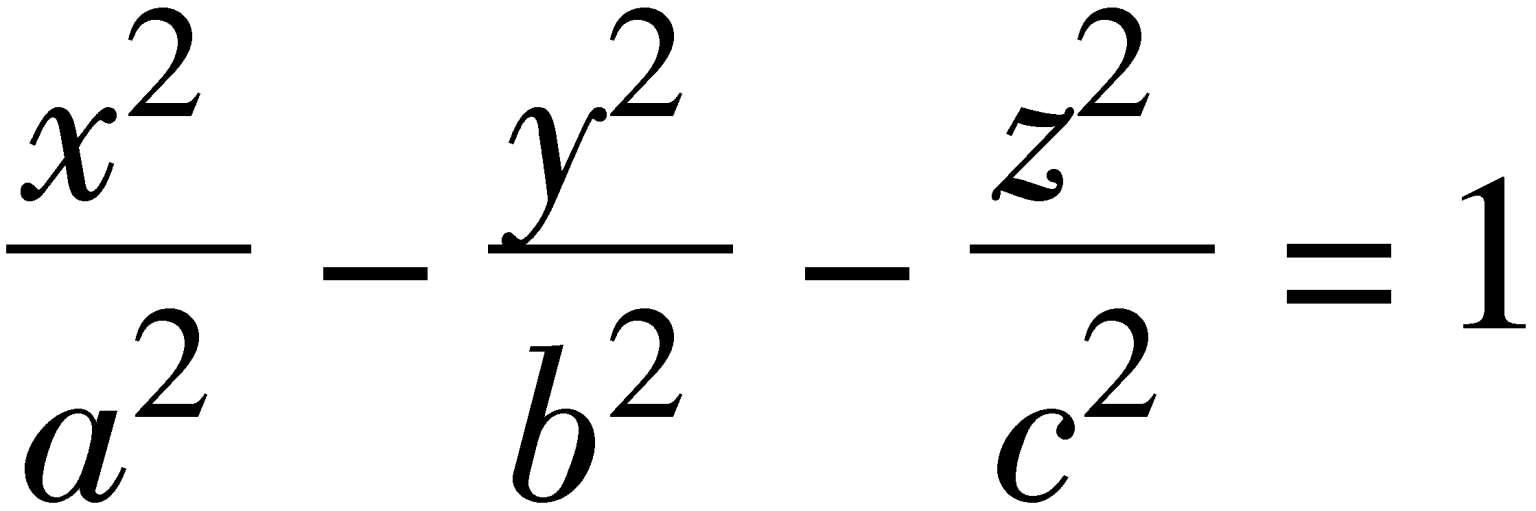
所表示的曲面称为“双叶双曲面”。它具有不相连的两个部分,关于yOz平面成对称。它与平行于xOy平面或xOz平面的平面的截线都是双曲线,而与平行于yOz平面的平面x=k(|k| >a)的截线都是椭圆。
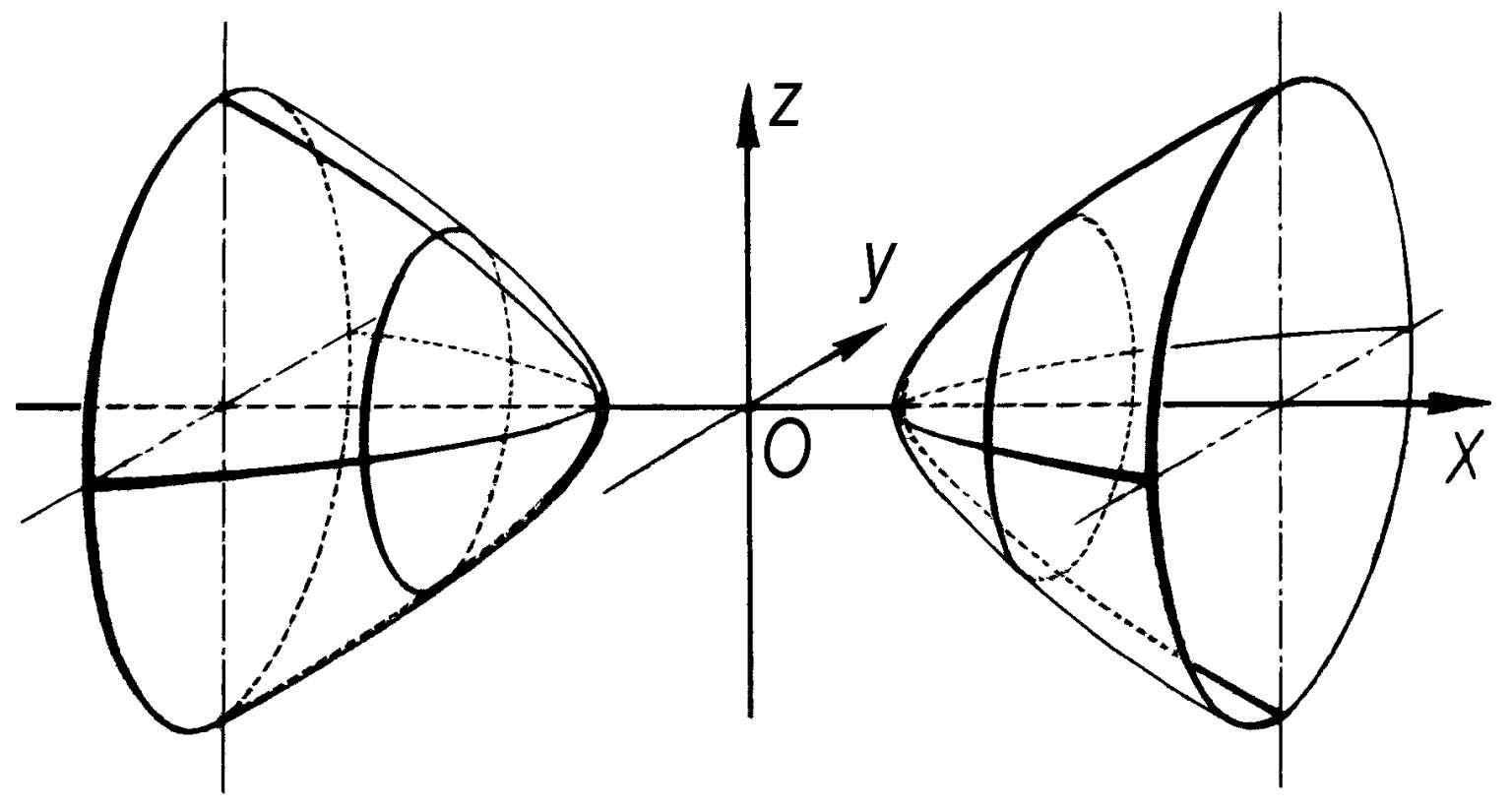
双叶双曲面
抛物面 二次曲面的一种。分椭圆抛物面和双曲抛物面两类。
椭圆抛物面
设(x,y,z)是直角坐标,则由标准形方程
 所表示的曲面称为“椭圆抛物面”。它与平行于xOy平面的平面的截线是椭圆,与垂直于Ox轴或Oy轴的平面的截线是抛物线。
所表示的曲面称为“椭圆抛物面”。它与平行于xOy平面的平面的截线是椭圆,与垂直于Ox轴或Oy轴的平面的截线是抛物线。
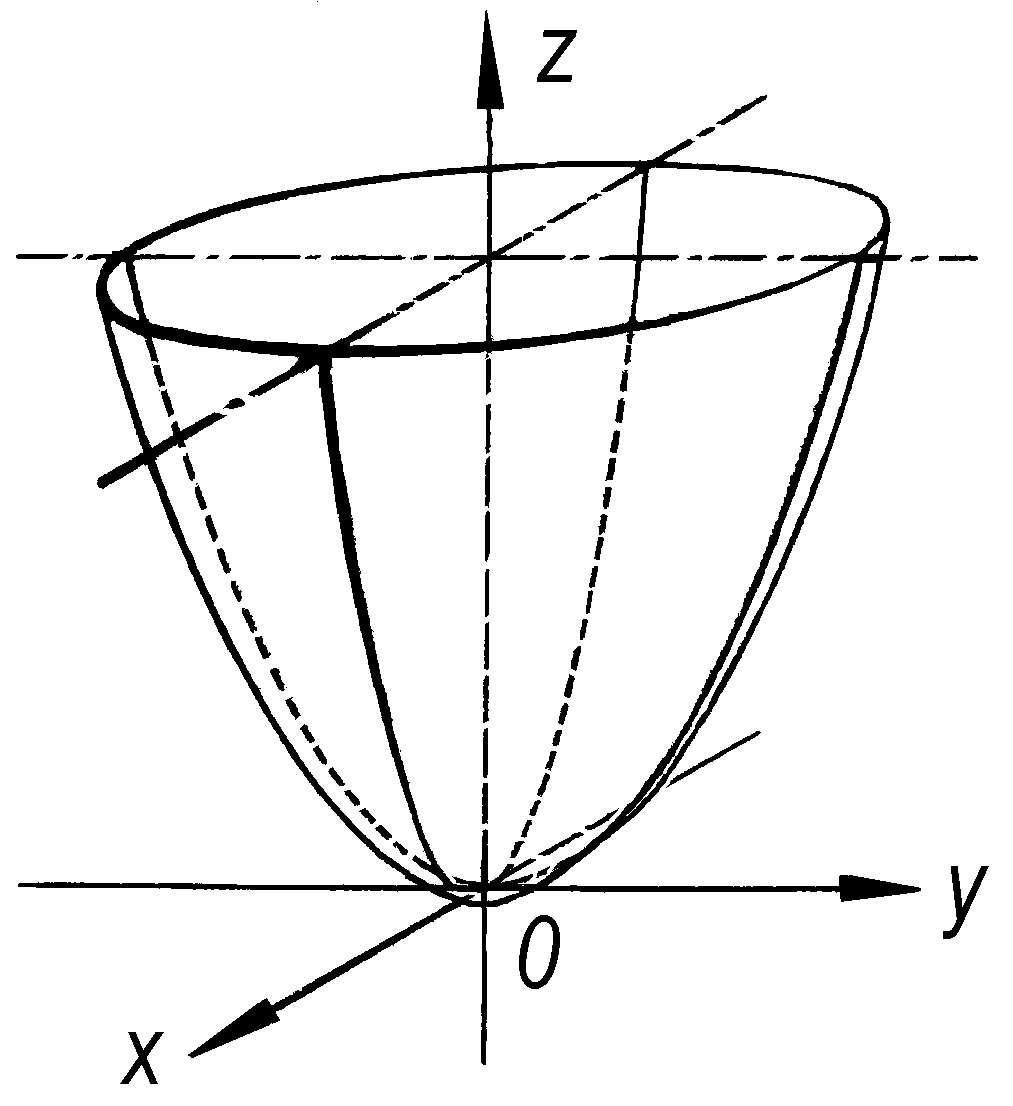
椭圆抛物面
双曲抛物面 设(x,y,z)是直角坐标,则由标准形方程
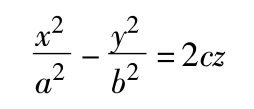
所表示的曲面称为“双曲抛物面”。它与平行于xOy平面的平面的截线是双曲线,与垂直于Ox轴或Oy轴的平面的截线都是抛物线。它是具有两组母线的直纹面。
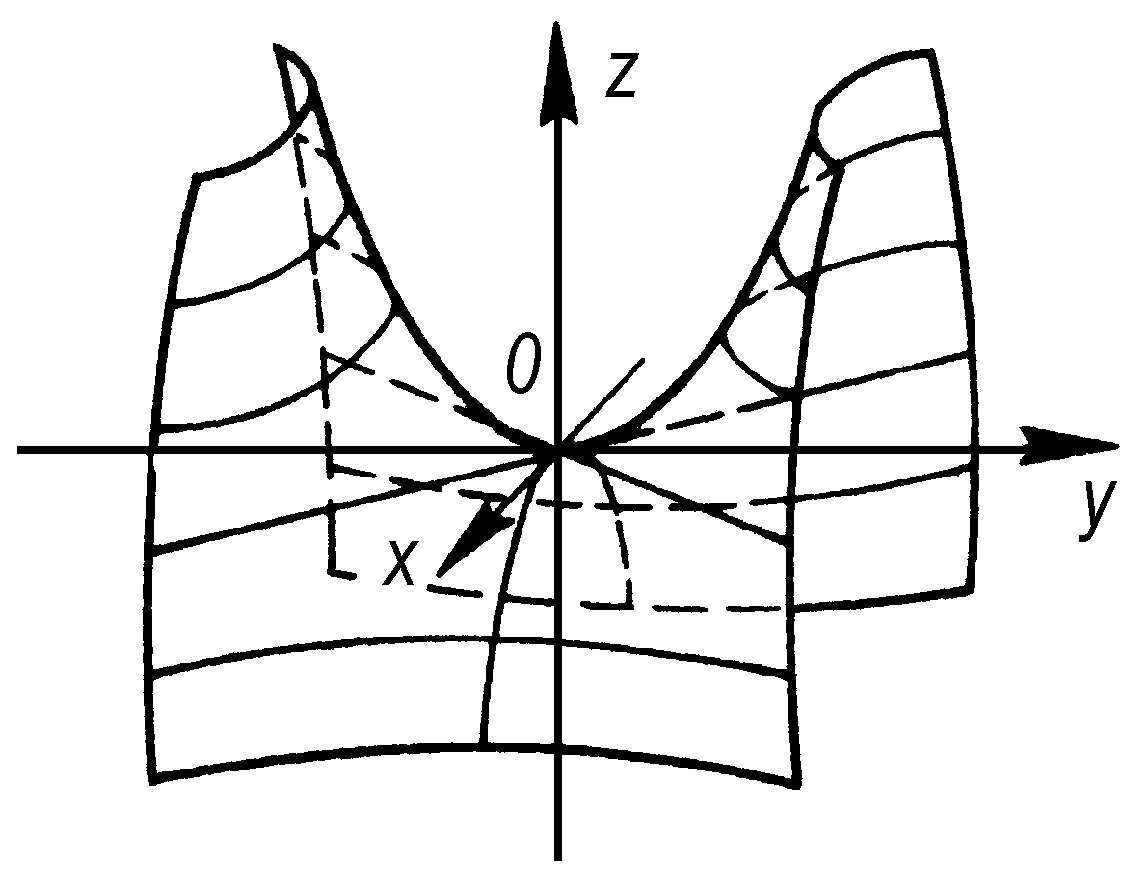
双曲抛物面
旋转面 平面曲线绕同平面上的一条直线在空间中旋转而成的曲面。曲线称为旋转面的“母曲线”,直线称为旋转面的“旋转轴”。如球面、圆柱面等均为旋转面。
旋转轴 见“旋转面”。
旋转体 封闭的旋转面围成的几何体。此时,旋轴面的轴也是旋转体的轴。圆柱、圆锥、圆台、球等都是旋转体。
螺旋线 一点沿旋转面的母线移动,该母线又绕旋转面的轴线作等角速旋转时所形成的空间曲线。如该旋转面为一圆柱面,一点沿圆柱面的直母线作等速移动时所形成的螺旋线称为“圆柱螺旋线”。螺旋线有右旋和左旋之分。如以拇指指向此点沿母线移动的方向,其余四指指向此点旋转方向,与右手符合的称“右旋螺旋线”,与左手符合的称“左旋螺旋线”。
正螺面 与旋转轴垂直相交的一条直线,在绕轴以匀角速度旋转的同时还沿轴方向匀速上升,这条动直线按上述运动方式所织出的曲面称为“正螺面”。
环面 轮胎状的曲面。一个圆周绕一条与圆周处于同一平面的圆外直线旋转而成的曲面。
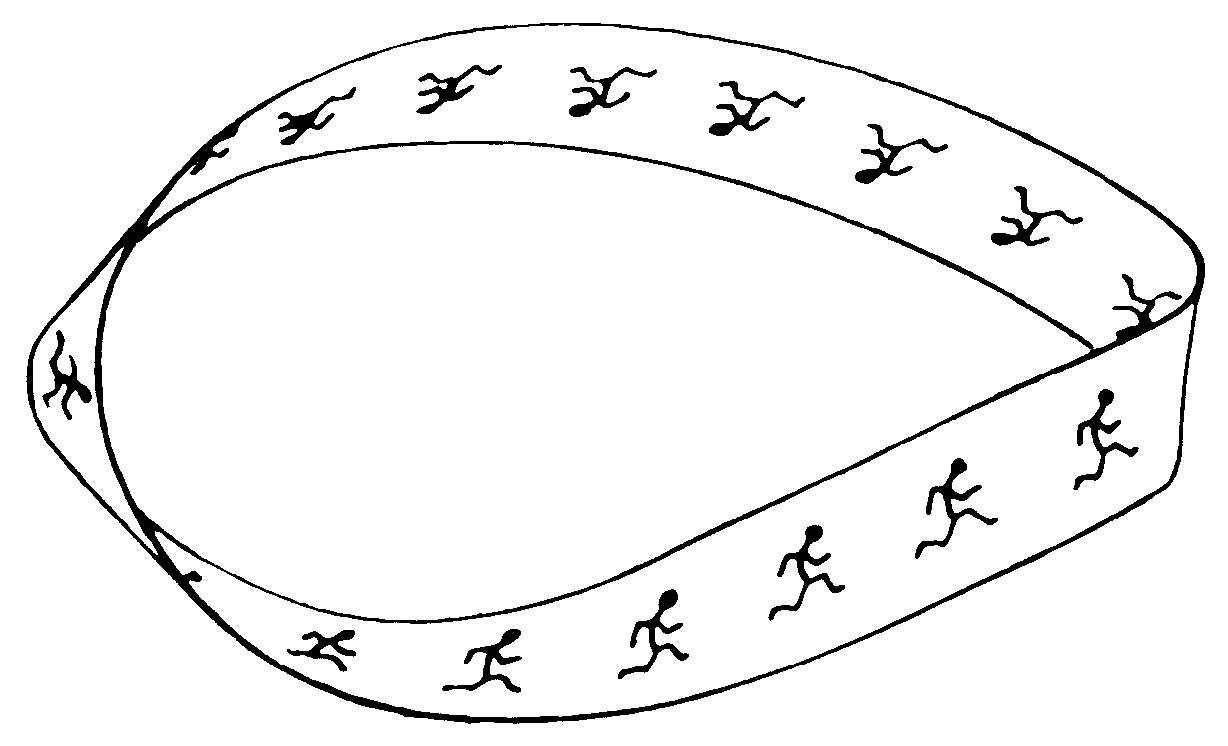
牟比乌斯带 将一条狭长的长方形纸带的一端扭转半周后与带的另一端粘贴而成的曲面(如图)。从这个曲面上任一点出发可以不经过带的边缘而连续变动到初始点的“背面”,具有这种性质的曲面称为单侧曲面。因德国数学家牟比乌斯首先发现而得名。
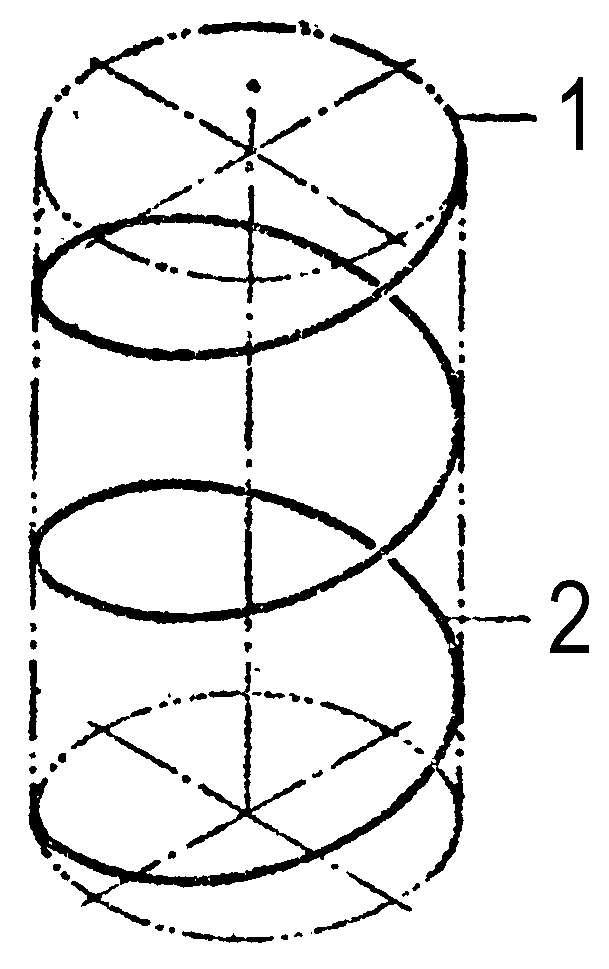
圆柱螺旋线(右旋)
1.正圆柱2.螺旋线
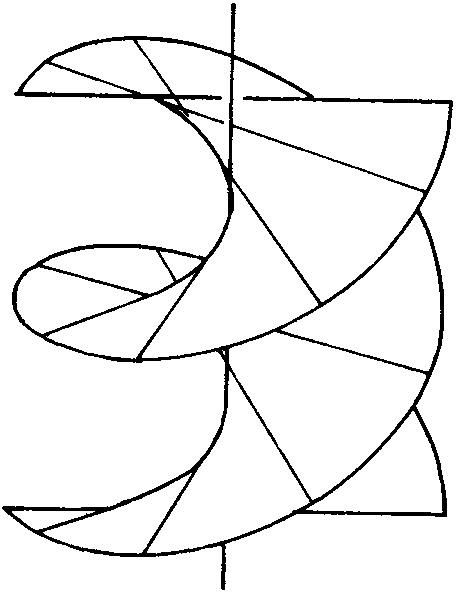
正螺面
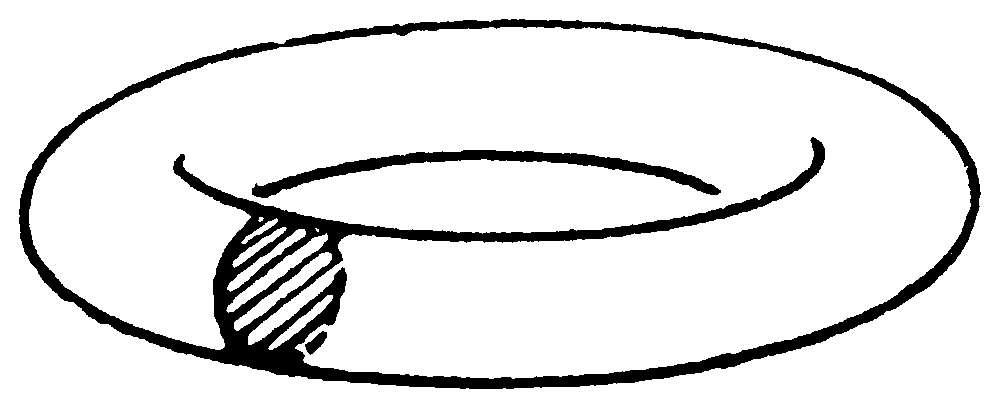
环 面
牟比乌斯带
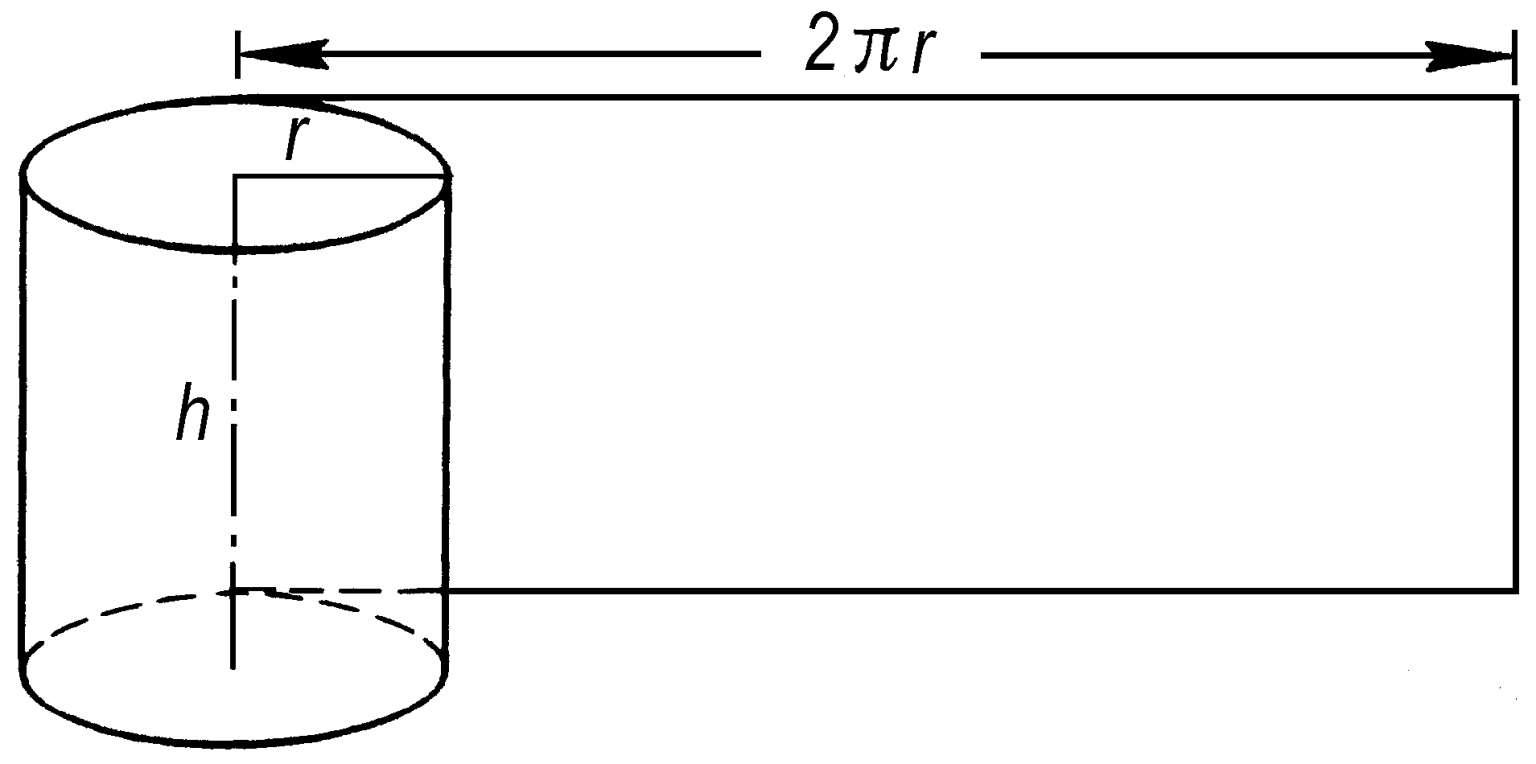
可展曲面
可以展开在一平面上的曲面。如柱面、锥面等。展开所得的平面图形称为原曲面的“展开面”。例如,高为h、底面半径为r的圆柱面沿母线的展开图是一个矩形,它两边的长分别为h和 2
 r。
r。
可展曲面
切线面 一种特殊的可展曲面。是由一条定曲线在每点处的切线编织而成的曲面。该定曲线就称为这个切线面的“脊线”。
脊线 见“切线面”。
测地线 曲面上的一种曲线。在曲面上的一个小范围内,它是连接曲面上两个点的最短的曲线。球面上的测地线是大圆,在大地测量中常有应用。
极小曲面 平均曲率为零的曲面。将一根弯成闭曲线状的铁丝浸入皂液中,再将其取出时,由于表面张力的作用,以铁丝为边界形成了一个皂膜曲面。此皂膜曲面必为极小曲面。从数学上证明以已给空间闭曲线为边界的极小曲面的存在性,即所谓普拉托(J. A. Plateau, 1801—1883)问题,是一个十分复杂的问题。对极小曲面的研究是微分几何学和偏微分方程理论中一个重要的研究方向。
曲率线 曲面上的一类正则曲线。此曲线在各点处的切线正好是曲面在该点处的主方向。过正则曲面上的每点,必有两条曲率线通过,于是构成了曲面的曲率线网。
全曲率 亦称“高斯曲率”。衡量曲面在各点附近弯曲程度的一种量。它是在曲面每点处的两个主曲率的乘积。曲面的高斯曲率恒为常数。
高斯曲率 即“全曲率”。
平均曲率 衡量曲面在各点附近弯曲程度的一种量。它是在曲面每点处的两个主曲率的算术平均。极小曲面的平均曲率恒为零。
弗伦内标架 曲线论中的重要概念。在以弧长s为参数的空间曲线 r = r (s)的各点处由曲线的单位切向量 T ,单位主法向量 N 及单位从法向量 B 所构成的右手系标架。因法国数学家弗伦内(Jean Fredéric Frenet, 1816—1900)而得名。借助于弗伦内标架,空间曲线的基本方程可写为
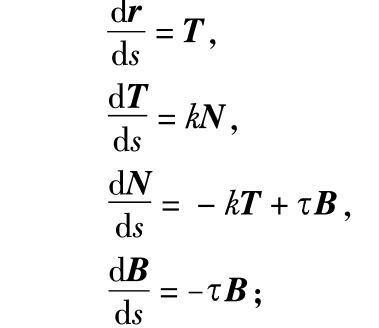
其中k为曲线的曲率,
 为曲线的挠率。上面后三个式子被称为弗伦内公式,它表明了沿着曲线走动时,沿途的弗伦内标架的变化情况。曲线论的各种几何性质都可从这组弗伦内公式中推导出来。
为曲线的挠率。上面后三个式子被称为弗伦内公式,它表明了沿着曲线走动时,沿途的弗伦内标架的变化情况。曲线论的各种几何性质都可从这组弗伦内公式中推导出来。
活动标架法 微分几何中一种常用的研究方法。在研究一个流形的几何性质时,并不选用固定的标架,而是在各点选用不同的、富有几何含义的标架,并在这些随点变动的标架下描述各种几何量之间的联系,这样就容易揭示出流形的几何本质。此方法由法国数学家嘉当首创。
裴蜀定理 ❶代数曲线论中计算两条代数曲线交点个数的定理。因法国数学家裴蜀(Etienne Bézout, 1730—1783 )而得名。一般地说,阶数分别为m和n的两条代数曲线相交于m·n个点,且不能超过m·n个点,除非他们有公共的分支(即定义这两条曲线的多项式具有公因子)。这也可叙述为:如P和Q是没有公共根的两个多项式,则存在另外两个多项式A和B,使得AP +BQ = 1。❷即“剩余定理”(63页)。
欧拉示性数 把二维闭曲面剖分成若干个曲边三角形,这些曲边三角形的顶点数减去曲边的条数再加上曲边三角形的个数,称为这个闭曲面的欧拉示性数,记作χ。欧拉示性数是一个拓扑不变量,它与所采用的剖分方式无关。令χ= 2 -2g,称g为此闭曲面的“亏格”。直观上,亏格是闭曲面所含洞的个数,例如,球面的亏格为 0,环面的亏格为 1。可利用亏格数来对闭曲面进行分类。
亏格 见“欧拉示性数”。
高斯
-
博内公式
微分几何中的一个著名公式:在整个闭曲面上高斯曲率的积分值等于闭曲面欧拉示性数的 2
 倍。由德国数学家高斯和法国数学家博内(Ossian Bonnet, 1819—1892)得出的这个公式揭示了曲面的几何性质与拓扑性质之间的紧密关系。陈省身等将此公式推广到高维黎曼流形,对整体微分几何的发展起了重要作用。
倍。由德国数学家高斯和法国数学家博内(Ossian Bonnet, 1819—1892)得出的这个公式揭示了曲面的几何性质与拓扑性质之间的紧密关系。陈省身等将此公式推广到高维黎曼流形,对整体微分几何的发展起了重要作用。
协变导数 适用于弯曲空间的一种导数。在平直空间中一个对象(如函数、向量等)的导数是先求出在无限邻近两点P、Q处的差商,再让Q点趋于P点,差商的极限就是此对象在P点处的导数。在弯曲空间的情形,差商不能简单地通过对象分量的差值来计算,必须将Q点处的对象运用平行移动的办法移植到P点,然后在同一点P处去计算差商。这样求出的导数称为协变导数。弯曲空间上张量场的协变导数必定是一个张量场。类似地,可建立协变微分的概念。
协变微分 见“协变导数”。
外微分形式 表达式
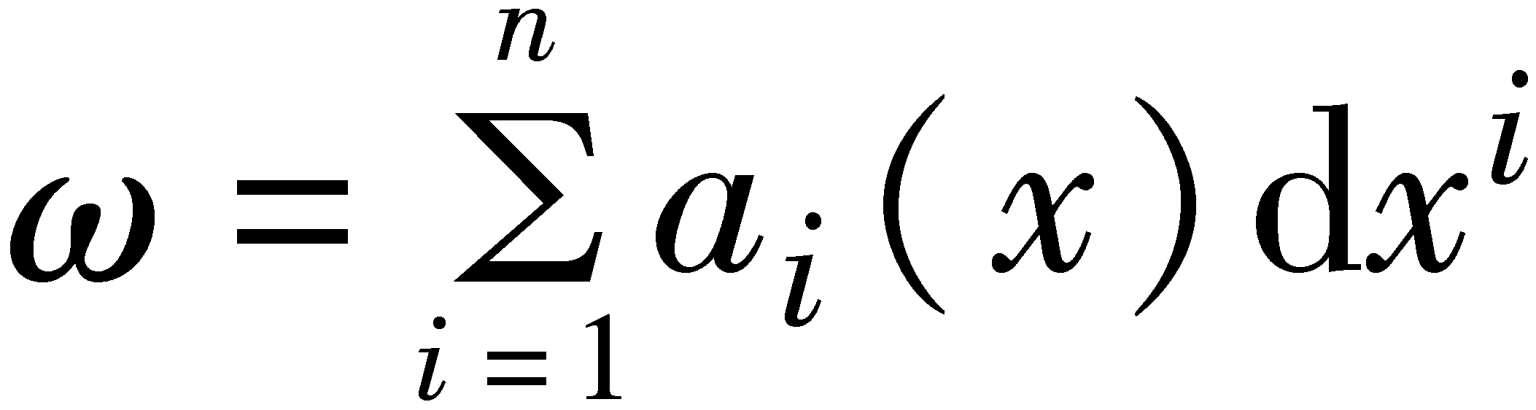
称为一次的微分形式,引进记号dx i ∧dx j ,并规定
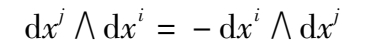
为dx j 和dx i 的外积。表达式
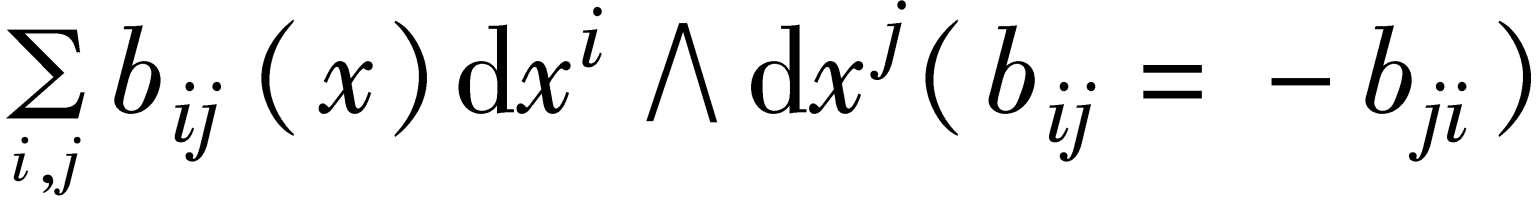
称为二次的外微分形式,而称
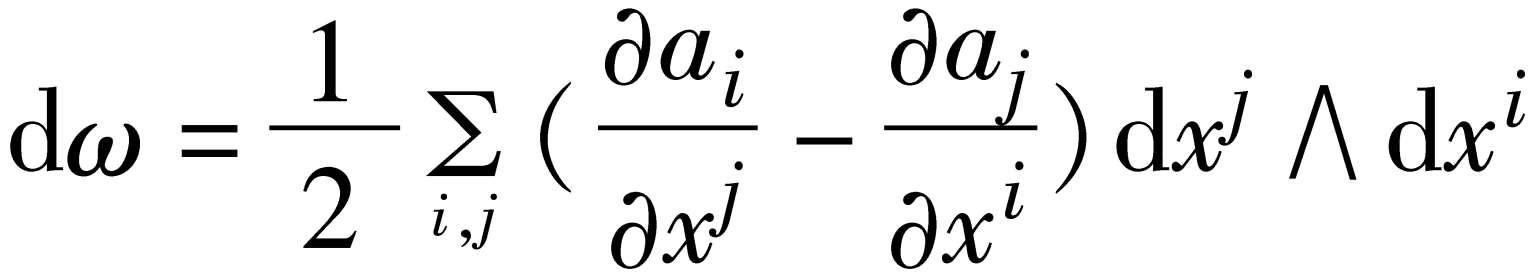
为ω的外微分。类似地,可以定义高次的外微分形式,且对它们作外积与外微分。k重外微分形式实际上是k维曲面积分中出现的微分式。因外微分形式是研究流形上的微积分的基本工具,对微分几何、微分拓扑和理论物理有很大的作用。
微分形式 简称“形式”。见“外微分形式”。
闭形式 外微分后为零的外微分形式,即满足dω= 0 的微分形式ω。
正合形式 可表为另一微分形式α的外微分的微分形式ω,即有ω= dα。
辛几何 微分几何学的一个分科。它研究辛流形的几何性质。这里的辛流形是指一个偶数维的微分流形,其上容有一个处处非退化的、闭的 2 形式(称为辛形式)。辛几何对分析力学和微分方程动力系统理论有重要的作用。
拓扑学 释文见 2 页。
一般拓扑学 亦称“点集拓扑学”。拓扑学的分支之一。主要研究拓扑空间的自身结构及其间的连续映射。是从关于实数集和实函数的研究中发展起来的。在引进了拓扑空间的概念和拓扑空间之间连续映射的一般定义后,从紧致性、连通性、收敛性、分离性、可数性等角度研究拓扑空间及其间连续映射的性质。它是泛函分析、整体微分几何、概率论等的基础。
点集拓扑学 即“一般拓扑学”。
代数拓扑学 拓扑学的分支之一。用代数方法研究空间的拓扑性质,即对于一个拓扑空间,让它对应于一个代数对象(如同调群、同伦群等),并使这个代数对象的结构与不变量能反映出空间的拓扑性质。包括同调论与同伦论等内容。
微分拓扑学 拓扑学的分支之一。主要研究微分流形在微分同胚下不变的性质及微分流形之间的可微分映射性质,诸如一流形能否嵌入另一个流形之中;若两个流形同胚,则是否为微分同胚;什么流形是另一个紧致流形的边界等问题。
拓扑空间
拓扑学研究的基本对象。它是一个集合,在其中以一定的规则来规定一个无限的元素序列是否收敛于一个元素,这种规定往往由某些公理来给出,称为拓扑结构。最简单的拓扑空间是实数轴和欧氏空间(依普通意义下的收敛性)。拓扑空间之间可以定义连续映射的概念,它是连续函数的推广。在拓扑空间中有开集、闭集、紧致性及连通性等概念。拓扑空间中元素的收敛概念也可通过开集来规定。拓扑空间X中的开集全体
 也称为该空间的“拓扑”。为强调X中的拓扑
也称为该空间的“拓扑”。为强调X中的拓扑
 ,也用(X,
,也用(X,
 )来表示拓扑空间。
)来表示拓扑空间。
拓扑 见“拓扑空间”。
连续映射 拓扑学的基本概念之一,微积分中连续函数概念的推广。对映射f∶X→Y,如Y的任意开集在f下的原象总是X中的开集,则称f是从X到Y中的连续映射。对于满足第一可数性公理的拓扑空间X,映射f∶X→Y在x∈X处连续的充要条件是:对X中收敛于x的任意序列{x n },序列{f(x n )}在Y中必收敛于f(x)。
覆盖 一般指开覆盖。拓扑空间中的一族开集,它们的并集填满了整个空间。
连通性 一种重要的拓扑性质。如果拓扑空间不能表示成两个不相交的非空开子集的并集,则称此拓扑空间是连通的拓扑空间。如果拓扑空间中一个子集作为子空间是连通的,则称此子集为连通子集。拓扑空间的极大连通子集称为连通分支。实直线上的连通子集必为区间。
紧致性 简称“紧性”。一种重要的拓扑性质。如果在拓扑空间的任意开覆盖中总可挑选出一个有限的子覆盖,则称此拓扑空间为紧致的拓扑空间。如果拓扑空间中一个子集作为子空间是紧致时,则称此子集为紧致子集。紧致性在连续映射下保持不变。实直线上的闭区间[a,b]是紧致的。欧氏空间中的紧致集等价于有界闭集。
子空间
拓扑空间中的子集采用诱导拓扑所形成的拓扑空间。设(
 )是拓扑空间,A是X的子集,由空间X的拓扑
)是拓扑空间,A是X的子集,由空间X的拓扑
 可以诱导出子集A的一个拓扑
可以诱导出子集A的一个拓扑
 A
= {A∪
A
= {A∪
 ,称
,称
 为
为
 的子空间,
的子空间,
 A
称为子空间拓扑或相对拓扑。球面上的拓扑通常就取由三维欧氏空间所诱导的子空间拓扑。
A
称为子空间拓扑或相对拓扑。球面上的拓扑通常就取由三维欧氏空间所诱导的子空间拓扑。
商空间
藉助于拓扑空间中点之间的等价关系所构造出的新的拓扑空间。设
 是一个拓扑空间,R是X上的一个等价关系,用X/ R表示X关于R的等价类所成的集合,
是一个拓扑空间,R是X上的一个等价关系,用X/ R表示X关于R的等价类所成的集合,
 ∶X→X/ R是自然投影,它将x∈X映成x所属的等价类。令
∶X→X/ R是自然投影,它将x∈X映成x所属的等价类。令
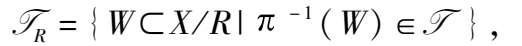
则
 是X/ R上的拓扑,称为商拓扑。拓扑空间(
是X/ R上的拓扑,称为商拓扑。拓扑空间(
 )称为(X,
)称为(X,
 )关于等价关系R的商空间。设S
n
是n维球面,如果将对径点看成是等价的,则这样得到的商空间即为n维实射影空间。
)关于等价关系R的商空间。设S
n
是n维球面,如果将对径点看成是等价的,则这样得到的商空间即为n维实射影空间。
拓扑基
生成拓扑空间中拓扑的一类集族。设(
 )是拓扑空间,
)是拓扑空间,
 是
是
 的子族。如果任意
的子族。如果任意
 都可表示为
都可表示为
 中某些集合的并集,则称
中某些集合的并集,则称
 为拓扑
为拓扑
 的基。因此对拓扑空间中所有开集的研究常可归结为对基中开集的研究。例如,所有开圆域的全体就构成了欧氏平面拓扑的一组基。
的基。因此对拓扑空间中所有开集的研究常可归结为对基中开集的研究。例如,所有开圆域的全体就构成了欧氏平面拓扑的一组基。
同胚 亦称“拓扑等价”。拓扑学基本概念之一。设f是两个拓扑空间之间的一对一映射,并且f和它的逆映射f - 1 都连续,就称f是两个拓扑空间之间的同胚映射,或称这两个空间同胚。例如球面和立方体表面同胚,但和环面不同胚。从拓扑学的观点看,两个同胚的空间本质上是相同的。如同胚f及其逆映射f - 1 都是可微分的,就称f是微分同胚。
微分同胚 见“同胚”。
流形 拓扑空间的一种。它的主要特征是:在其上每一点都有一邻域(即含该点的开集),它和n维欧氏空间的一个区域建立了一对一的、双方连续的映射。粗略地说,它是由一块块和欧氏空间的区域相同胚的那种几何图形“拼接”而成。球面、环面、牟比乌斯带、射影平面等都是流形。如果这种拼接可以做到很光滑,使得在流形上能够有办法定义无限次可微分的函数,那么这流形称为“微分流形”。流形是拓扑学的重要研究对象。微分流形又是各种几何结构的“载体”,如其上有黎曼度量(参见 84 页“黎曼几何”),则称它为“黎曼流形”,是整体微分几何的最重要的研究对象。
微分流形 见“流形”。
黎曼流形 见“流形”。
黎曼曲率张量 反映黎曼空间“弯曲”程度的一种张量。从黎曼空间中的一点P出发,将P点的一个向量沿着从P点出发的一条环路平行移动,当回到原来出发点时,平行移动的向量一般并不一定回到原来向量的位置。黎曼曲率张量就是被用来表达这个偏差量。利用黎曼曲率张量可进一步导出诸如里奇曲率张量、数量曲率等一系列反映黎曼空间弯曲程度的几何量。
子流形 流形的一个子集。它在流形的诱导拓扑及诱导微分结构下,本身也构成了一个流形。
浸入 拓扑学中一类重要的映射。从一个流形到另一个流形的一种特殊的非奇异映射,使得在映射的定义域内的每一点处,映射的导数是一个线性单射。这相当于说,该映射局部地看上去像是一个从低维的欧氏空间到高维的欧氏空间中的包含映射。
嵌入 两个拓扑空间之间的一种映射。在这种映射f∶X→Y下,流形X的拓扑性质与(作为Y的子流形的)象集f(X)的拓扑性质完全一致。例如,有理数嵌入于实数之中,整数嵌入于有理数之中。又如在几何中,球面被嵌入为三维欧氏空间中的单位球面。
豪斯多夫空间 一类重要的拓扑空间。对这种空间中的任意两个不同的点A、B,必存在着包含A点的开邻域U A 及包含B点的开邻域U B ,使得U A 、U B 互不相交。
仿紧空间 一种常见的豪斯多夫空间。对它的每一个开覆盖,必存在着一个局部有限的、开的细化。仿紧性是拓扑空间中的一个较为普遍的性质,它类似于紧致性,但范围略“大于”紧致性。任何流形都是仿紧的。
纤维丛 拓扑学的重要研究对象。是乘积空间的一种推广。在流形M的每一点都附上一个空间,各点所附的空间的构造是相同的,并容有群的作用,但附着的方式可能有扭曲,称这种空间为“纤维”,称这种群为“结构群”,所有纤维的全体就构成了“纤维丛”,而称流形M为纤维丛的“底流形”。如果所取的群与纤维一致,则为“主纤维丛”。如取纤维为向量空间,取结构群为一般线性群,则为“向量丛”。它在微分几何、理论物理等方面均有重要作用。
主纤维丛 简称“主丛”。见“纤维丛”。
向量丛 见“纤维丛”。
示性类 刻画向量丛拓扑性质的一种拓扑不变量。示性类理论最初是由惠特尼和斯蒂费尔(Eduard Stiefel, 1909—1978)在 1935 年分别开始研究的。常用的示性类有陈(省身)类、庞特里亚金类、欧拉类及斯蒂费尔-惠特尼类等。示性类在微分几何、多复变函数论等研究中被广泛地运用。
联络 欧氏空间中向量平行移动概念的一种推广,是从黎曼几何中的列维-齐维塔平行性发展而来的。它建立了流形上两无限邻近点处的切空间中向量之间的一一对应关系(也称为平行移动)。由此可产生协变微分的概念。让切向量沿流形上一条微小环路平行移动一周后不一定返回原处,衡量它与初始向量的偏差的量称为联络的曲率,它是曲面上高斯曲率的一种推广。联络的挠率是衡量联络偏离对称性的一种量。联络的概念可推广到一般的主纤维丛及向量丛中去,从而形成了纤维丛上的联络理论。它在微分几何等学科中起了重要的作用。主纤维丛上的联络理论在理论物理中也有重要的作用。1954 年杨振宁(1922— )和密尔斯(Robert Mills, 1927—1999)提出的规范场,从数学上看就是主纤维丛上的联络。
单形 亦称“单纯形”。拓扑学的基本概念之一。它是点、线段、三角形、四面体等图形的推广。对n维欧氏空间中的n+ 1个固定点P 0 ,…,P n ,可表为形如
的点的全体(其中λ 0 ,…,λ n 是非负实数,且它们的和为 1),称为以P 0 ,…,P n 为顶点的一个单形。点、线段、三角形、四面体分别是零维、一维、二维、三维单形。在单形的n+ 1 个顶点中选出r+ 1 个顶点,并以这些点为顶点所构成的子单形称为原来单形的r维面。
单纯复合形 有限个单形所构成的集合K,如果K中任何两个单形的交集是空集,或者是K中另一个单形的面,则称K为单纯复合形。称单纯复合形中若干个p维单形的线性组合为p维链。对每个链可施行边界运算。如果某链的边界为零,则称此链为闭链;如某链为另一链的边界,则称原来的链为边界链。由此可定义同调群的概念。如果拓扑空间同胚于一个单纯复合形,则称此拓扑空间是可剖分的。流形是可剖分的空间。
同伦 代数拓扑学的基本概念之一。空间中的一条闭曲线如能连续变形到另一条闭曲线,则称这两条曲线在这个空间中是同伦的。这概念可推广到一般的拓扑空间中去,从而产生了同伦群及映射的同伦等概念。研究拓扑空间的各种同伦群的性质和映射的同伦分类问题,形成了代数拓扑学的一个重要分支——同伦论。
同调 代数拓扑学的基本概念之一。单纯复合形中的一个r维循环如果恰为另一个(r+ 1)维循环的边界,则称此r维循环同调于零;如两个循环的差同调于零,则这两个循环是同调的。由此可产生同调群、上同调群等概念。研究拓扑空间的各种同调群的性质就形成了代数拓扑学的一个重要分支——同调论。
基本群 拓扑空间最基本的拓扑不变量。首先由庞加莱于 1895 年引进。即以给定的基点p为起点和终点的闭路径在同伦的等价关系下所形成的群。这个群的乘法采用路径的合成,恒等元是所有同伦于由点p所构成的常值路径的集合。相互同胚的空间的基本群是同构的。基本群与基点的选取无关,它描述了空间X的同伦性质。如果空间的基本群是平凡的,则称此空间是单连通空间,即在这类空间中的任何路径均同伦于常值路径。
单位分解
把流形的局部性质整体化的重要工具。给定一个具有开覆盖
 的光滑流形M,所谓单位分解是指:存在一族光滑的非负函数{φ
i
}使得φ
i
的支集被包含在U
i
之中,且处处成立
的光滑流形M,所谓单位分解是指:存在一族光滑的非负函数{φ
i
}使得φ
i
的支集被包含在U
i
之中,且处处成立
 。如果开覆盖{U
i
}是一个局部有限覆盖,则对每点x∈M,仅有有限多个i,使得φ
i
(x)≠0。单位分解能用来将定义在局部区域上的对象拼合成一个定义在整个流形上的对象。利用单位分解可以得出:在仿紧流形上必存在着整体定义的黎曼度量。
。如果开覆盖{U
i
}是一个局部有限覆盖,则对每点x∈M,仅有有限多个i,使得φ
i
(x)≠0。单位分解能用来将定义在局部区域上的对象拼合成一个定义在整个流形上的对象。利用单位分解可以得出:在仿紧流形上必存在着整体定义的黎曼度量。
上同调群 拓扑空间的一个不变量。它与“同调群”是互相对偶的,所以它能反映出空间中“洞”的性质,但是上同调包含了比同调更多的代数结构。
德拉姆上同调 微分流形的一种拓扑不变量。由瑞士数学家德拉姆(Georges de Rham, 1903—1969)提出。它是利用流形上的外微分形式来构造的。微分流形上的正合形式一定是闭形式,但闭形式就不一定是正合形式。这是由于微分流形的拓扑复杂性所引起的。因此闭形式全体关于正合形式全体所得出的商空间就在一定程度上反映出微分流形的拓扑性质。这种商空间具有自然的群结构,被称为德拉姆上同调群。当流形是紧致时,德拉姆上同调群与流形的奇异上同调群是同构的。
皮亚诺曲线
能够填满正方形区域的一条连续曲线。因首先由皮亚诺发现而得名。将闭区间I和闭正方形Q=I×I分别作四等分(如图),得到I
0
,I
1
,I
2
,I
3
和Q
0
,Q
1
,Q
2
,Q
3
。再将这样得到的I
i
和Q
i
继续进行四等分,得到I
ij
和Q
ij
(i,j= 0,1,2,3),如此继续进行,以至无穷。对闭区间序列
 …及闭正方形序列Q
i
…及闭正方形序列Q
i
 可分别确定出I中唯一的点t
ij
k…及Q中唯一的点
可分别确定出I中唯一的点t
ij
k…及Q中唯一的点
 (k= 0,1,2,3)。任意x∈I必可表为
(k= 0,1,2,3)。任意x∈I必可表为
 令f(x)=q
ijk
…后就得出了一个连续满射f∶I→Q,称为皮亚诺曲线。它的发现对深入理解连续性及曲线的概念有很重要的意义。
令f(x)=q
ijk
…后就得出了一个连续满射f∶I→Q,称为皮亚诺曲线。它的发现对深入理解连续性及曲线的概念有很重要的意义。
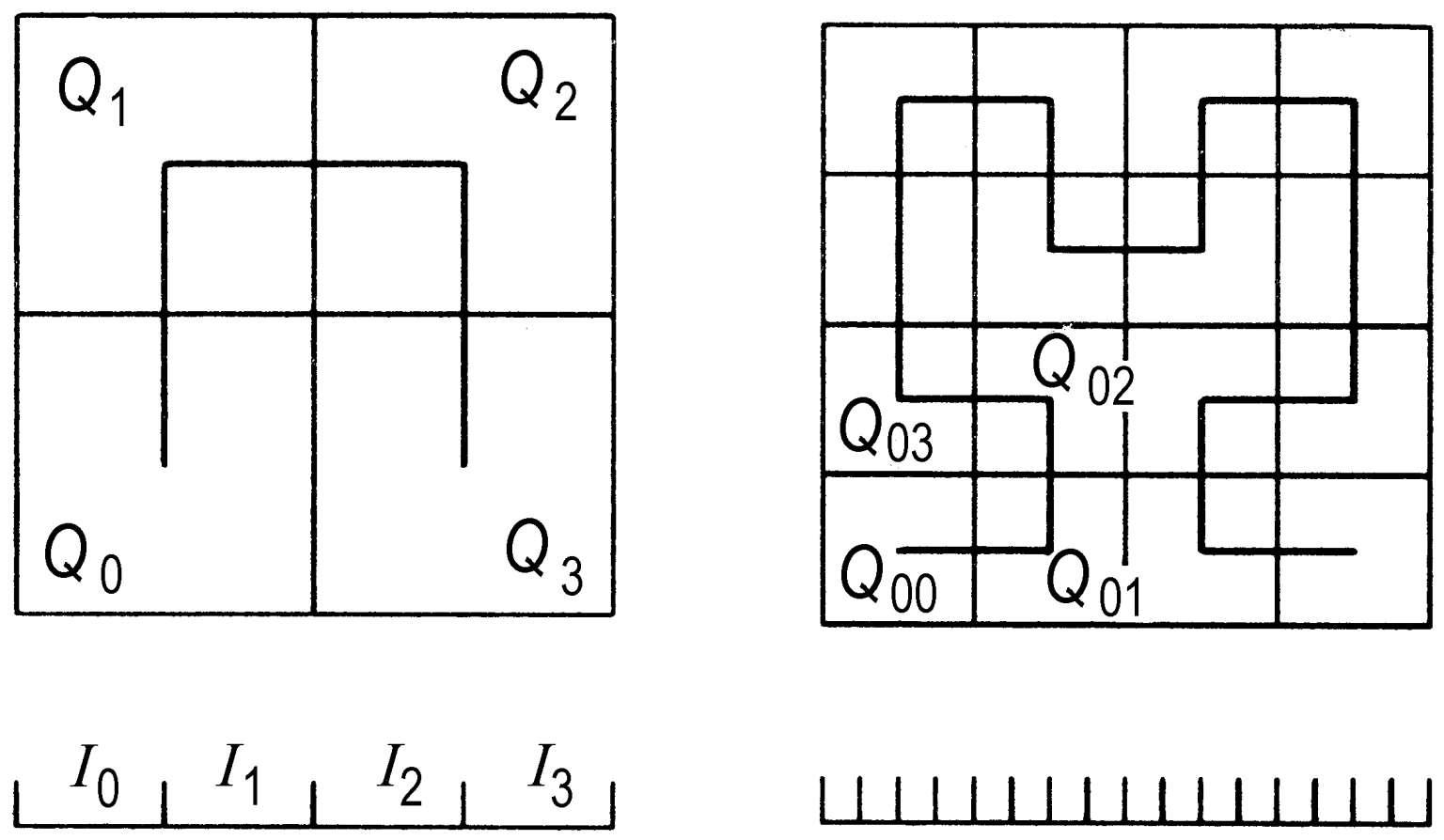
皮亚诺曲线
克莱因瓶 一个不可定向的闭曲面。是由德国数学家克莱因在 1882 年发现的。将正方形的两组对边分别按照图示的箭头方向叠合后得到的曲面。从这构造方法可知,沿着它上面一条适当的闭曲线剪开,就成为牟比乌斯带,因此它是不能定向的。它不能在三维欧氏空间中以嵌入曲面(不能自身相交)的方式显现。下图是克莱因瓶的示意图。
克莱因瓶
四色问题 拓扑学和图论中有名的问题。指能否只用四种颜色在地图上把所有的地区涂色,使相邻的两个地区颜色不同。1976 年美国阿佩尔(K. Appel)等人宣布借助电子计算机证明了用四色染图是足够的。
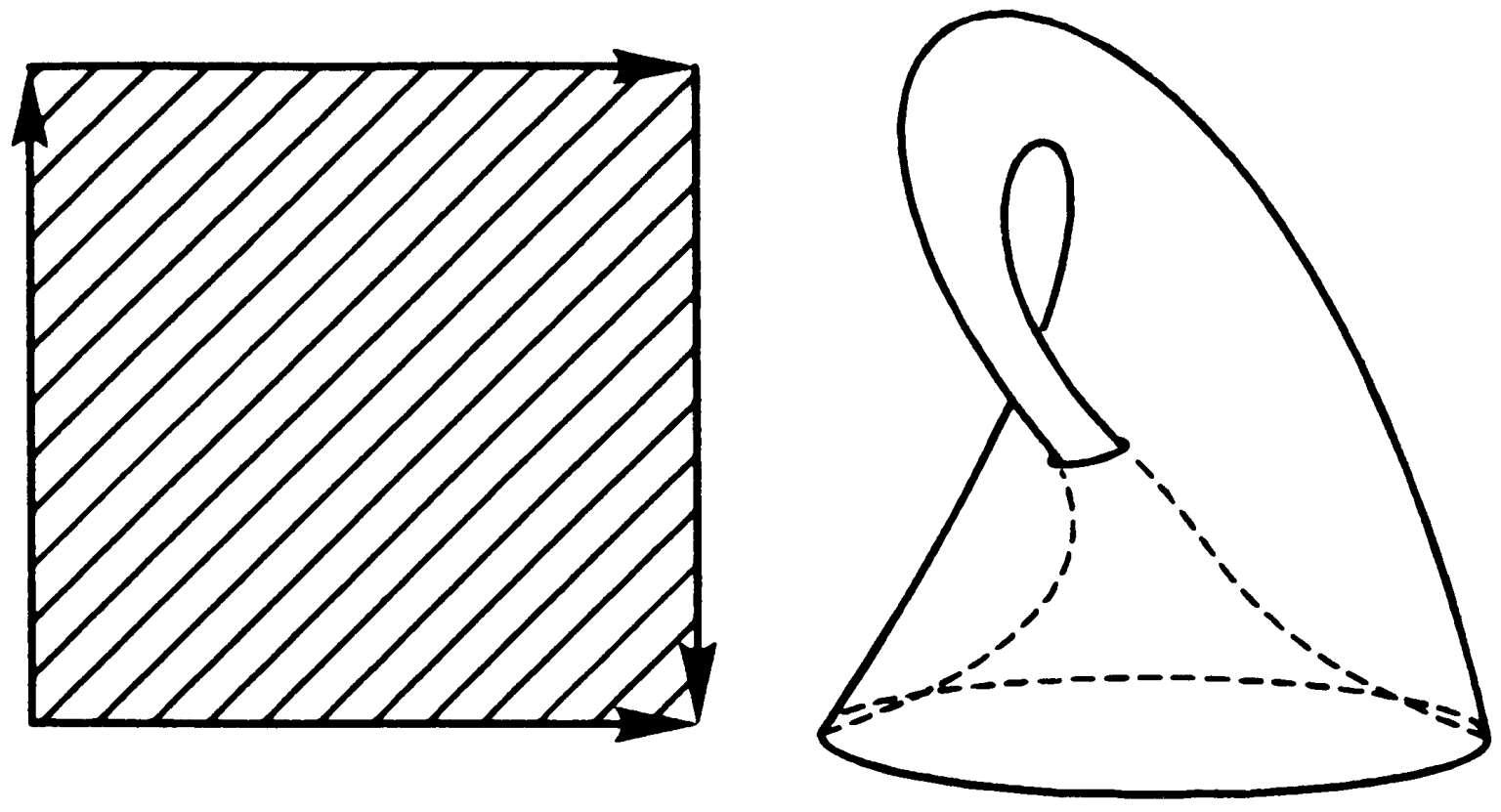
纽结理论 拓扑学中研究绳结、链锁等几何现象的一个分支。纽结是绳圈的一种数学抽象,即三维空间中一条连续的、自身不相交的封闭曲线。纽结理论的基本问题是判定两个不同的纽结能否相互连续变形。1883 年高斯引进了闭曲线的环绕数。20 世纪,随着拓扑学的研究而有很多进展,可用群和不变多项式来表示纽结的拓扑性质,特别是 1984 年新西兰数学家琼斯(Vaughan Frederick Randal Jones,1952— )在研究算子代数时发现了琼斯多项式,能用来分辨出许多不能相互连续变形的纽结。更重要的是由此找到了纽结理论与量子统计力学、量子场论之间的紧密联系。它还可用来分析分子生物学中的DNA实验。
不动点理论 拓扑学和分析学中的一个重要理论。主要研究拓扑空间(如定向闭曲面、环状区域、多面体)到自身的连续映射有没有不动点的问题,同时也研究不动点的个数以及寻求不动点的方法。有压缩映射原理、布劳维不动点定理等。代数方程、微分方程的许多求解问题可归结为求某个映射的不动点问题,因而该理论在数学的许多分支中有着广泛的应用。
庞加莱猜测 拓扑学中最著名的猜测。法国数学家庞加莱于 1900 年提出了下述猜测:每一个紧致单连通的三维流形必与三维球面同胚。德国数学家胡尔维茨(Witold Hurewicz, 1904—1956)提出了如下的广义庞加莱猜测:与n维球面S n 具有相同同伦群的n维单连通紧致流形必与S n 同胚。斯梅尔(Stephen Smale, 1930— )于 1961 年证明这一猜测在n> 4 时是正确的。1981 年,弗里德曼(Michael H. Freed man, 1951— )证明了当n= 4 时的情形也是正确的。


