运筹学·组合数学
运筹学 释文见 3 页。
规划论 亦称“数学规划”。运筹学的分支。计划管理工作中有关安排和决策的问题,一般可以归纳为在满足既定的要求下,按某一衡量指标来寻求最优方案的问题,规划论就是对这类问题从数学理论和数学方法上作系统的研究。典型的例子是所谓“运输问题”,即将数量和单位运价都给定的某种物资从多个供应站运输到不同的消费站,要求在供销平衡的同时,定出流量和流向,使总运费为最小。通常称必须满足的条件为“约束条件”,衡量指标为“目标函数”,所寻求的最优方案为“最优解”。如目标函数和描述约束条件的数学方程和不等式都是线性的,则称为“线性规划”,否则称为“非线性规划”。如所考虑的规划问题与时间有关,则称为“动态规划”。如所考虑的规划问题与有限个事物的组合或排列有关,则称为“组合规划”或“组合最优化”。按规划问题的类型不同,还有“随机规划”、“多目标规划”等。规划论在经济管理和工程设计等方面有广泛的应用。
数学规划 即“规划论”。
目标函数 见“规划论”。
约束条件 见“规划论”。
最优解 见“规划论”。
最优性条件 与规划论中最优解相关的条件。它有助于分析最优解的性质和寻求最优解。有最优性必要条件,也有最优性充分条件。按条件中涉及目标函数导数的最高阶数,确定最优性条件的阶数,最常见的是一阶和二阶的最优性条件。
线性规划 运筹学中实际应用最广泛的一个分支。其中心论题是求线性函数在线性(不等式或等式)约束下达到最小(大)值的问题。20 世纪 30 年代末由康托洛维奇等人开始研究,40 年代后美国数学家丹齐格(George Bernard Dantzig,1914—2005)提出了有效的单纯形法,进一步奠定了它的数学基础。不仅应用于企业规划、工农业生产管理等方面,其思想还渗透到自然科学和社会科学的许多领域。
单纯形法 一种求解线性规划的常用方法。主要利用线性规划的特点:变量的取值范围在几何上相当于一个多面体,最优方案可在变量取该多面体的顶点时达到。单纯形方法的计算过程就是不断地调整变量的取值,从一个顶点到达另一相邻的顶点,使新的方案优于原来的方案,最终求得最优方案。
运输问题 一类特殊的线性规划问题。参见“规划论”。
图上作业法 求解运输问题的一种方法。是 20 世纪 50 年代由中国粮食调运工作者与数学工作者共同从实践中总结出来的。它将物资的产销地以及运输路线都画在一张交通图上,然后在图上进行计算。
表上作业法 求解运输问题的一种方法。是将解一般线性规划问题的单纯形法结合运输问题的特点而设计的。由于用这种方法解规模较小的问题时,可以在一种表格上进行计算,故而得名。
非线性规划 见“规划论”(161 页)。
二次规划 目标函数为二次函数,且约束条件为线性方程与(或)线性不等式时的规划问题。二次规划问题在实践中经常出现,还可在求解非线性规划的算法中应用。已经研究出许多求解二次规划的数值方法。
凸规划 规划论的一个分支。当目标函数为凸函数,且约束条件所确定的集合为凸集时,该规划问题称为“凸规划”。线性规划与二次规划都是凸规划的特殊情形。
整数规划 规划论的一个分支。决策变量取整数值的线性规划或非线性规划。在研究具有离散性的决策问题中,往往要用到整数规划。例如,在一项工程中,如何安排人力或有限种设备而使效果达到最优,便是一个整数规划问题。如果在整数规划问题中进一步限制决策变量取值只能为 0 或 1 (称为布尔变量),那么该问题称为布尔规划问题。布尔规划可应用于电路设计、设备管理等方面。
布尔规划 见“整数规划”。
分枝定界法 一种解整数规划以及其他离散最优化问题的常用方法。它通过对决策变量取值范围的划分,把问题分成一些子问题(这一过程称为分枝);分别求出它们的最优目标值或者最优目标值的界,然后相互比较,抛弃一些非最优决策的取值范围(这一过程称为定界);重复这些过程,直至找出问题的最优决策。
背包问题 整数规划的一个典型问题。旅行者临行前打算从许多物品中挑选一些物品放入一只体积固定的背包,给定这些物品的体积和价值,应如何选取放入背包的物品使总价值最大?这就是背包问题。
动态规划 规划论的一个分支。立足于整体利益,研究多阶段决策过程的理论和方法。它既研究离散的决策过程,也研究连续的决策过程。依照问题中状态转移规律,有确定性和随机性之分。求解主要依据基于最优性原理的动态规划基本方程,把问题化为依次求解多个含较少变量的单阶段最优性问题。在系统工程、自动控制、经济管理等领域都有应用。
随机规划 规划论的一个分支。约束条件与目标函数中具有随机系数或其他随机项的线性规划问题,称为随机规划。研究具有随机性的决策问题中,往往要用到随机规划。例如,研究某些生产活动时,产品的未来需要量应作为随机变量,过多或过少的产量都会有某种“偿付”,如何安排这些生产活动,而使这时的收益在扣除“偿付”后达到最大,便是一个随机规划问题。
多目标规划 规划论的一个分支。若规划问题中的衡量指标即目标函数不是一个,而是若干个,那么该问题就是多目标规划问题。如企业生产中往往要求取得较多的利润和总产值,同时又要损耗较少;如何安排生产,就是一种多目标规划问题。多目标规划与经济学、决策分析、系统理论等有密切的联系。
最优化方法 解决最优化问题的方法。所谓最优化问题,指在某些约束条件下,决定某些可选择的变量应该取何值,使所选定的目标函数达到最优的问题。主要研究数学规划与最优控制这两类问题的求解方法。由于实际的需要和计算技术的进步,最优化方法的研究发展迅速。
非光滑优化 最优化方法的一个分支。研究目标函数与约束条件为非光滑函数的情形。在非光滑优化的最优性条件中,需将微积分中导数的概念扩充为非光滑函数的次微分的概念。非光滑优化的方法可用于工程与经济中一些比较复杂的实际问题。
优选法 一种旨在提高效率的方法。在科学试验和生产工艺条件选择中,它可用以合理安排试验,以较少的试验次数找到合理的配方、合适的工艺条件等。它所依据的是数学上寻找函数极值(极大或极小)点的较快的计算方法。常用的有黄金分割法等。20 世纪 70 年代经著名数学家华罗庚倡导,优选法在中国得到推广和应用。
黄金分割法 亦称“0.618 法”。寻求单峰函数极值点的一种优选法。区间上一个点将区间分为两段,若小段与大段之比等于大段与区间全长之比,则称该点为黄金分割点,这个比值约为 0.618。通过对某区间上的黄金分割点及其在该区间的对称点(即大段的黄金分割点)两个函数值的比较,使最优解所在的区间快速地缩小,从而得到近似的最优解。
0 . 618 法 即“黄金分割法”。
单峰函数 若单变量函数为单调函数,或它可分成分别为单调递增和递减函数的两段,则称为“单峰函数”。
统筹法 亦称“计划评审法”、“关键路线法”。企业管理和基本建设中安排工作进程的一种运筹学方法。根据生产要求、劳动力、设备和物资的情况以及工艺流程,排出带有数据的箭头图,据以找出施工进度中的主要矛盾线(亦即关键路线),及时调度,以保证或加快工作的进程。也可以考虑工艺流程中的随机因素,对整个计划的完工情况做出预先的评估与调整。
计划评审法 即“统筹法”。
关键路线法 即“统筹法”。
组合最优化 亦称“组合规划”。见“规划论”(161 页)。
匹配问题 组合最优化的一个重要问题。给定一个集合,在若干约束条件下,要使不含公共元素的二元组达到最多,或者使这样的二元组所相应的某个指标之和达到最大。
网络流 组合最优化的一个重要内容。由一组给定的点、若干连接这些点的边以及这些边上某种数值(长度、运费或流量界限等)所组成的总体称为“网络”。在一个网络中可以指定若干点为产地,若干点为销地,网络流就是从产地出发沿着运输路线将产品送到销地的一种安排。网络流的主要研究内容是:在许多安排中寻找“流量”最大或者费用最小的安排。
流动推销员问题 亦称“旅行商问题”、“货郎担问题”。组合最优化的一个重要问题。一个推销员准备去若干城市推销商品,然后回到出发地。已知各城市之间的距离,应怎样选择一条既经过每个城市恰好一次,总距离又最短的路线?这就是流动推销员问题。在应用上有重要意义。
中国邮路问题 组合最优化的一个重要问题。一个邮递员要走遍社区中的每条街道,允许重复,如何走法能使总的路程最短?它等价于在图中重复设置某些边,使之具有欧拉环游,而这些边的总长度应当尽量短。在定向图上也有相应的邮路问题。该问题由中国数学家管梅谷于 1960 年首先研究并给出算法,故而称为中国邮路问题。
指派问题 组合最优化的一个重要问题。对多种不同的机器指派不同的工作,怎样使这种指派所产生的效益达到最大?它可由有效的算法来求解。
对策论 亦称“博弈论”。运筹学的一个分支。运用数学理论研究有利害冲突的各方在竞争性的活动中是否存在自己取胜的最优策略,以及如何找出这些策略等问题。1912 年德国数学家策梅罗首先用数学方法研究象棋对策问题,1928 年冯·诺伊曼证明了有关两人零和矩阵对策的主要结果,奠定了对策论的理论基础。对策论在经济、军事等方面均有应用。
博弈论 即“对策论”。
排队论 亦称“随机服务系统理论”。运筹学的一个分支。起源于有关自动电话的研究。主要研究具有随机性的排队现象,包括等待时间、排队长度等的概率分布。可应用于交通运输、仓库设计、计算机系统设计等方面。
存储论 运筹学的一个分支。是研究如何控制存储物资的理论。主要根据物资的性质、需求以及存储费用等因素,确定购买或生产物资的时间和数量等问题,以使其效益最大或相应的损失最小。例如,零件储备过多或因零件缺乏而停产都会带来损失。如何使此种损失减少到最小,就是存储论所研究的重要问题之一。
更新论 运筹学的一个分支。主要研究工业或军事设备应该在什么时候、采取什么样的策略来更换、维修、检查之类的问题。例如,当设备变得陈旧时,维修费和因停工所受的损失将日益增大,应在何时更换最恰当;某些军用设备的性能随使用时间而退化,需定期检查,应采取什么样的检查制度才使总的代价最少等。
搜索论 运筹学的一个分支。第二次世界大战中因研究如何搜索德军潜艇而发展起来的一种理论。主要研究如何将所掌握的资源、经费等分配到预备搜索的各个区域,使得能以最大的可能性、最小的代价找到搜索的目标。该理论除了用于军事外,也用于民用事业,如寻找矿藏、寻找复杂设备出现故障的原因等。
时间表理论 亦称“作业调度理论”、“排序理论”。运筹学的一个分支。主要研究如下类型的作业调度问题:有一批工件要在一组机器上加工,已知每个工件的加工时间及应交货工期,如何安排这批工件在这组机器上的加工次序及时间表,使某个目标函数达到最优。时间表理论的研究涉及组合最优化与计算复杂性。
作业调度理论 即“时间表理论”。
决策分析 对多种决策进行比较与选择的定量分析方法。允许决策后的事件是随机的,通过建立效用函数进行分析。效用函数的不同取法体现决策者的意向。一个好的决策分析,常要经过多次反复才能完成。基于主观概率和效用理论之上的决策分析理论由英国逻辑学家拉姆赛(Frank Plumpton Ramsey,1903—1930 )首先提出。
军事运筹学 研究有关军事问题的定量分析及决策优化的理论与方法的学科。主要是通过运用数学模型、电子计算机技术等,揭示各种军事系统的结构、功能及其运行规律,为科学地进行军事活动、合理地利用资源,提供相应的依据。
组合数学 释文见 3 页。
组合计数 组合数学的一个重要内容。主要研究各种计数问题的解法和规律。所谓计数问题,指给定一个集合,要求出某种子集或某种排列的总数。计数中常用的方法有加法原理、乘法原理、容斥原理、递归关系、生成函数等。
容斥原理 组合数学中关于计数方法的一个基本原理。它可表示为:具有性质A或B的元素个数等于具有性质A的元素个数与具有性质B的元素个数之和,减去同时具有性质A和B的元素个数。还可推广到多个集合的情形。
递归关系 在数列中或其他数学量的序列中,若任何一项可由以前若干项按某一关系式来确定,则该关系式称为递归关系。发现与分析递归关系,对于研究各种序列及算法设计,常有重要作用。
生成函数
亦称“母函数”、“发生函数”。对于实数列{a
n
},在实数域上定义的形式级数
 就称为数列{a
n
}的“生成函数”。x为不定元,它可以是数,也可为抽象的符号。由于形式级数可以很方便地像解析函数一样进行运算,因此可将其作为工具来研究相应的数列。瑞士数学家欧拉首先利用它来求解组合计数问题。
就称为数列{a
n
}的“生成函数”。x为不定元,它可以是数,也可为抽象的符号。由于形式级数可以很方便地像解析函数一样进行运算,因此可将其作为工具来研究相应的数列。瑞士数学家欧拉首先利用它来求解组合计数问题。
母函数 即“生成函数”。
卡塔兰数 设n为自然数,

称为卡塔兰数。它是许多计数问题的解。例如,求n元a 1 ,a 2 ,…,a n 在不改变顺序的条件下,可以构成不同结合顺序的乘积个数;答案就等于C n 。卡塔兰(Eugéne Charles Catalan, 1814—1894 ),比利时数学家。
更列 亦称“重排”。设有按顺序排列的n个元a 1 ,a 2 ,…,a n ,要求将它们重新排列,使得没有一元在原先位置,此类排列即称“更列”。用D n 表示n元所有更列的个数,称为“更列数”,则
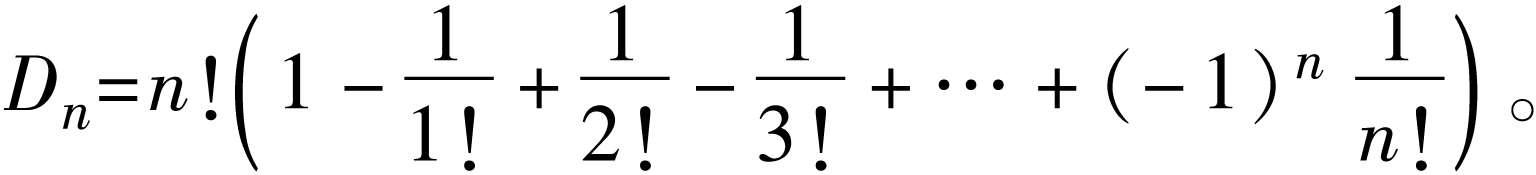
更列数也可由下述递归关系来确定:
更列是组合数学的著名古典问题,最早的形式是:把n封信任意套进已写好的信封,求n封信都套错信封的可能情形有几种?瑞士数学家欧拉首先解决了这个问题。
重排 即“更列”。
夫妻问题 组合数学中的著名古典问题。由法国数学家吕卡(François -Édouard -Anatole Lucas,1842—1891)提出。设有n对夫妻围圆桌而坐(坐位已标号),要求男女相间且夫妻不相邻,问有多少种不同坐法?用M n 表示n对夫妻的就坐方法,则有M n =2n!U n ,其中U n 称为“夫妻数”。最前面的几个夫妻数如下表:

抽屉原理 亦称“鸽笼原理”。组合数学中的一个基本原理。可表述为:将一定数量的物品放入若干个抽屉,如果放入的物品数大于抽屉数,则至少有一个抽屉放有两件或两件以上的物品。该原理还可推广为面积的重叠原理。
鸽笼原理 即“抽屉原理”。
组合设计 组合数学的一个重要内容。对任何可行试验,事先都要根据试验目的、事物特征和有关主要因素进行设计,组合设计主要用组合数学方法研究设计的存在性、组合特征及构造方法,研究如何将一些元素排成若干组,使之满足规定的要求。包括正交拉丁方设计和区组设计等。应用于产品试验设计等方面。
拉丁方 将自然数 1,2,3,…,n排成n行n列的方阵,如果其每一行与每一列中都没有重复的数,则称该方阵为n阶拉丁方。由于最早用来构造这种方阵的符号是拉丁字母,故名。如图是一个三阶拉丁方。

拉丁方
正交拉丁方 两个n阶拉丁方在同一位置上的数依次配置成对时,如果这些有序数对恰好各不相同,则称它们为正交拉丁方。例如,下面两个四阶拉丁方相互正交:
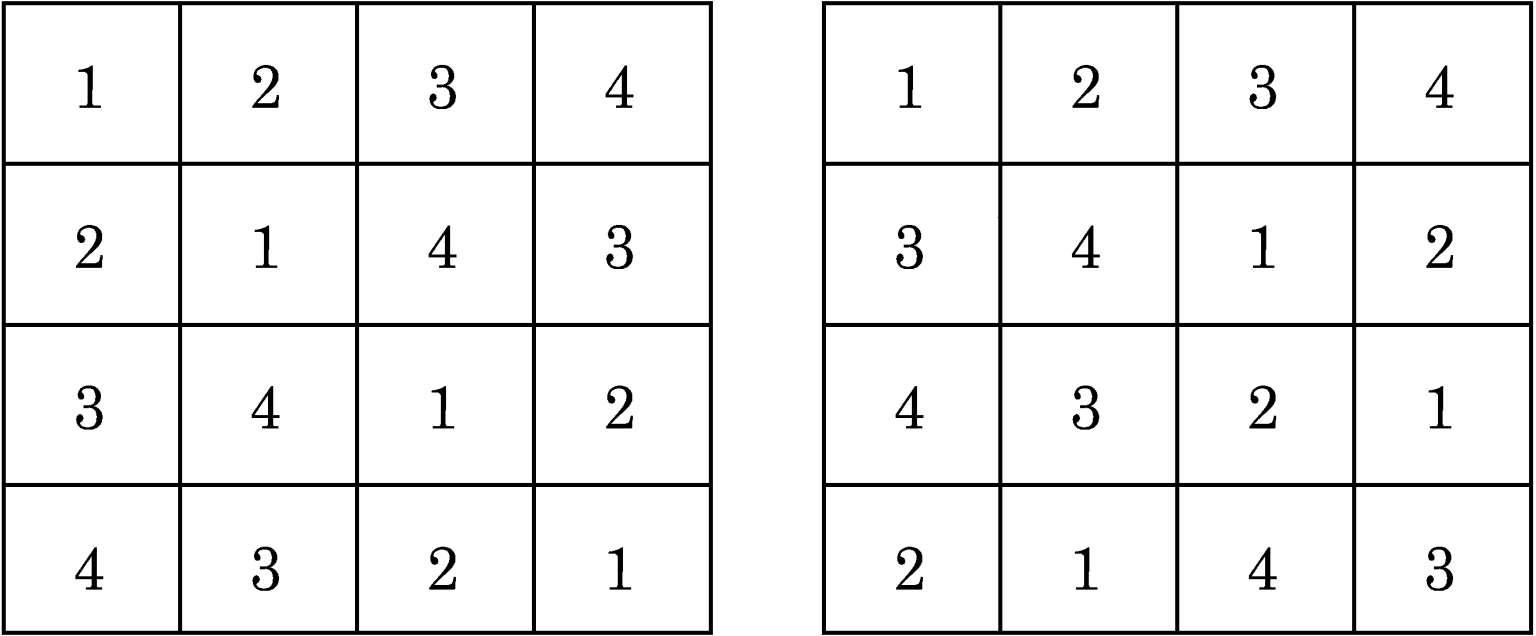
已经证明,除了n= 2,6 以外,任何阶的正交拉丁方都存在。正交拉丁方在组合设计中有重要应用。
区组设计 组合设计的一种重要类型。将一个大集合按照某些要求分为一些子集,称这些子集为区组。区组设计的主要问题是设计的分类、存在条件和某些类的构造方法。包括配对平衡设计、平衡不完全区组设计等。
配对平衡设计 组合设计的一种。由印度数学家鲍斯(Raj Chandra Bose,1901—1987 )和什里汉德(S.S.Shrikhande)于 1960 年首先建立。把v个元排列到b个子集(亦称区组)中,使每个子集包含k i (k i < v,i∈ {1,2,…,m})个相异元,且每对相异元恰同时出现在λ个子集中,则这b个子集构成一个“配对平衡设计”。(v;k 1 ,k 2 ,…,k m ;λ)构成此设计的参数组。如果k 1 =k 2 =…=k m =k,则配对平衡设计成为“平衡不完全区组设计”,简记为BIB。它与正交拉丁方、阿达玛矩阵、有限几何等有密切联系,是组合设计理论的主要内容。
平衡不完全区组设计 见“配对平衡设计”。
斯坦纳三元系 参数k= 3,λ = 1 的平衡不完全区组设计。因瑞士数学家斯坦纳而得名。一般用STS(υ)表示阶数为υ的斯坦纳三元系。其存在的充要条件是υ≥3,υ≡ 1 或 3(mod 6)。υ = 3,7,9 时,斯坦纳三元系唯一存在;υ = 13 时,恰存在2 个不同构的解;υ = 15 时,存在着 80 个不同构的解。
不相交斯坦纳三元系大集 如果两个斯坦纳三元系STS(υ)没有公共子集,就称为不相交。不相交STS(υ)的最大个数记为D(υ)。因为υ个元可以构成b(υ -2)个不同的三元子集,如果这些子集恰可组成υ -2 个不相交的STS(υ),则此υ -2 个不相交的STS(υ)就构成了υ阶“不相交斯坦纳三元系大集”,且D(υ)= υ -2。1850年英国数学家柯克曼证明了D(9)= 7,此后不相交STS(υ)(υ > 9)的存在性问题一直悬而未决,直至 1983 年才由中国数学家陆家羲彻底解决:若υ > 7,且υ∉{141,283,501,789,1501,2365 },则D (υ)=υ -2。
三十六个军官问题 瑞士数学家欧拉于 1782 年提出的著名组合数学问题:有来自 6 个不同团队且分属 6 种不同军衔的36 个军官,能否把他们排成 6 × 6 方阵,使每行每列的军官团队相异,且军衔亦不同?事实上,若团队和军衔都分别用数字1,2,…,6 表示,假设问题有解,则表示团队和军衔的数字分别构成拉丁方,且这两个拉丁方正交。因此,问题的实质就是 6阶正交拉丁方是否存在?1901 年数学家塔利(G. Tarry)首先证明了 6 阶正交拉丁方不存在,亦即该问题无解。
十五个女生问题 英国数学家柯克曼(Thomas Penyngton Kirkman,1806—1895)于 1847 年提出的著名组合数学问题:一名教师每天带领 15 个女生散步,15 个女生排成 5 × 3 队形,应该怎样编排,才能使每对女生在 7 天内恰好只有一次排在同一行?实际上,这是如何将 15 个女生的集合,分成 35 个三人组,使得每对女生出现并只出现在一个三人组。柯克曼利用可分解平衡不完全区组设计,巧妙地求出了问题的解。
阿达玛矩阵
设H
n
为元素是+1 或-1的n阶矩阵,
 为H
n
的转置矩阵,I
n
为n阶单位矩阵,如果
为H
n
的转置矩阵,I
n
为n阶单位矩阵,如果
 ,则称H
n
为n阶阿达玛矩阵。它是研究一类组合设计的有力工具。1893 年法国数学家阿达玛证明了:若n阶实矩阵的每个元素的绝对值都不大于1,则其行列式的绝对值不大于
,则称H
n
为n阶阿达玛矩阵。它是研究一类组合设计的有力工具。1893 年法国数学家阿达玛证明了:若n阶实矩阵的每个元素的绝对值都不大于1,则其行列式的绝对值不大于
 ,且H
n
是达到此上界的唯一矩阵,故而得名。
,且H
n
是达到此上界的唯一矩阵,故而得名。
有限几何 组合数学的一个重要内容。它的研究对象是由有限个“点”、“直线”、“平面”等构成的几何结构,虽然具有某种几何直观,但需借助于抽象代数的方法来研究有关性质。可应用于组合设计。
有限射影平面 有限几何的研究对象。欧氏平面的推广。由有限个称为“点”的元素和一些称为“线”的元素组成。其上定义关系:点P在直线L上(或等价关系:线L通过点P),且满足如下公设:(1)任意两个不同的点在且仅在一条直线上;(2)任意两条不同的直线过且仅过一个点;(3)存在四个点,其中任意三点都不在同一条直线上。将有限射影平面去掉一条直线及其上面的n+ 1 个点,可得到有限仿射平面。
有限仿射平面 有限几何的研究对象。由有限个称为“点”的元素和一些称为“线”的元素组成。其上定义关系“在”和“平行”,满足如下公设:(1)任意两个不同的点在且仅在一条直线上;(2)对任意给定的直线L及不在L上的点P,都有唯一的一条过点P且与L平行的直线;(3)存在不共线的三点。两条不相交的直线称为平行;所有直线可按平行分类,有n + 1 类,每类中有n条直线。如果对应每个平行类,添加一个无穷远点,让此类中直线都交于此无穷远点,并将这n + 1 个无穷远点作为一条“无穷远直线”,则可得到一个有限射影平面。
多项式算法 求解规模为n的组合最优化问题,如果其运算次数A的计算复杂度不超过规模n的某一多项式f(n),则称A为解此问题的“多项式算法”。
P 问题 凡能用多项式算法求解的组合最优化问题,均称“ P问题”。 P为英文多项式Polynomial的首字母。支撑树问题、匹配问题、网络流问题、中国邮路问题等都是P问题。
NP 问题 具有非确定性多项式算法的问题。 NP为Nondetermistic Polynomial两词的首字母。这类判定问题只对答案为“是”时,才有多项式算法检验其正确性;而对答案为“不是”时,无法给出多项式算法作论断。 P问题为NP问题的一个子类,但前者在后者中占据多少,甚至两者是否重合,至今还悬而未决。目前人们研究的组合优化问题均属NP问题。
NP 完全问题 简称“NPC问题”。具有如下共性的一类NP问题:(1)类中每一个问题都还未找到多项式算法;(2)若类中有一个问题是P问题,则类中所有问题都是P问题。 NP完全问题由库克(S. A.Cook)于 1971 年给出,至今已有近千个问题属于此类,包括哈密顿圈问题、0 -1 背包问题等许多著名问题,人们越来越相信NPC问题不是P问题。2000 年 5 月法国克莱(Clay)数学研究所悬赏解决七个千禧年数学难题,其中第一个问题就是NPC= P?
魔方 ❶“魔术立方体”的简称,亦称“鲁比克立方体”。玩具。匈牙利建筑师埃尔诺·鲁比克(Ernö Rubik, 1944— )于 1974 年发明。为一个正立方体,每个面分别由颜色相同的九个小方块组成,每个小方块固定位置,并能在三个不同的平面内旋转 360°。玩时将各面的小方块拧转,立方体的各面即变得花色斑驳,致一个魔方能千变万化,形成各种不同颜色的组合形式。要求玩者尽快使之复原。魔方游戏有助于提高人们的空间想像能力。❷即“纵横图”(49 页)。
图论 以直观图形与数学方法来研究组合关系的一门数学分支。其研究对象是图,它可代表某些数学对象之间的二元关系。直观地说,由一些给定的点及连接这些点的某些边所组成的总体称为“图”。七桥问题与四色问题等都是图论问题。由于研究的内容和方法不同,分别有组合图论、代数图论、拓扑图论、随机图论、结构图论、极值图论等分支。图论在计算机科学、运筹学、电子技术、通信科学、系统工程、经济学等方面都有应用。
图 图论的研究对象。由一些给定的点以及连接这些点的边所组成的总体称为一个图。若每条边皆有给定的方向,则称为“有向图”;否则称为“无向图”。若在图中从任何一点出发沿着边走总能到达另外任何一点,则称为“连通图”;否则,称为“不连通图”。对一个图来说,点可以代表某种数学对象,边可以代表这些数学对象之间的二元关系,因此图的研究有着广泛的应用。
有向图 见“图”。
无向图 见“图”。
连通图 见“图”。
简单图 在一个无向图中,两个端点重合的边称为环;两条具有相同端点的边称为重边;既无环又无重边的图就称“简单图”。图论中通常研究的即此类图。
完全图 任何两个顶点均邻接的简单图。n个顶点的完全图记作K n 。
圈 设想一人从图中一点出发沿着边走,最终回到起点,其间经过图中的点至多一次,这些边的全体就构成一个圈。
树 若连通图中不存在圈,则称为“树”。一个树或几个分离的树组成的图,称为“森林”。若一个树的每条边都有给定的方向,则称为“树形图”。

树
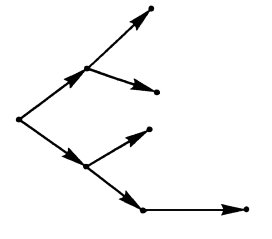
树形图
森林 见“树”。
树形图 见“树”。
生成树 亦称“支撑树”。由一个图的所有点和一些边构成,不含有圈而边数恰比点数少 1,称它为这个图的一个生成树。寻找一个图的生成树,使它所含的各边的距离之和达到极小,即所谓最小生成树问题。
支撑树 即“生成树”。
连通度 为了使图G成为不连通图或平凡图(只有一个顶点的图),从G中至少需要去掉的顶点数,称为图G的“连通度”或“点连通度”。而为了使图G成为不连通图或平凡图,从G中至少需要去掉的边数,就称为图G的“边连通度”。
色数 用k种颜色对图G的顶点染色,使相邻(有边相连)的顶点有不同的颜色,则称图G是k可着色。若G是k可着色,则一定是k+ 1 可着色。使图G是k可着色的最小正整数k称为G的“色数”,而称G为“k分图”。它可理解为对图G的顶点分类,使得着同一色的顶点为同一类。此时G的顶点集分成k类,每一类中的顶点互不邻接。
k 分图 见“色数”。
边色数 用k种颜色对图G的边染色,使相邻(有公共端点)的边有不同的颜色,则称图G是k边可着色。若G是k边可着色,一定是k+ 1 边可着色。使图G是k边可着色的最小正整数k称为G的“边色数”。
覆盖 有点覆盖和边覆盖两类。设K是图G的点子集,若G的每一条边至少有一个端点属于K,则称K为G的点覆盖。设M是图G的边子集,若G的每一个点均为M中边的端点,则称M为G的边覆盖。
点 ( 边 ) 独立集 设S是图G的顶点(边)子集,如果S中任意两点(边)在G中无边相连(无公共端点),则称S为G的“点(边)独立集”。图G的点(边)独立集中点(边)数最多的,称为最大点(边)独立集,其点(边)数称为G的点(边)独立数。通常简称点独立集为独立集。
可平面图 如果图G能画在平面上,使得它的边仅在端点相交,则称G为“可平面图”。这样的画法称为图G的一个平面嵌入。已经嵌入平面内的一个图,称为“平面图”。有时可平面图也简称为“平面图”。
平面图 见“可平面图”。
剖分图 设e是图G的边,剔除边e,并增加一个新点连接边e的两个端点,称为对边e剖分。对图G的边进行若干剖分所得到的图H,称为G的“剖分图”。
库拉托夫斯基定理 判定一个图是否为可平面图的定理。由波兰数学家库拉托夫斯基(Kazimierz Kuratowski,1896—1980)于 1930 年提出。图G是可平面图的充分必要条件是:G不包含K 5 或K 3 ,3的剖分图。其中K 5 为 5 个顶点的完全图;K 3 ,3 为由两个 3 顶点子集构成的完全二分图。
邻接矩阵 图的一种矩阵表示。它刻画了图中各顶点间的邻接关系。设图G的顶点集为V(G)={v 1 ,v 2 ,…,v n },若n阶方阵A(G)=(a ij )其元素a ij 是连接顶点v i 和v j 的边数,则称A(G)为图G的邻接矩阵。例如,下图的邻接矩阵为
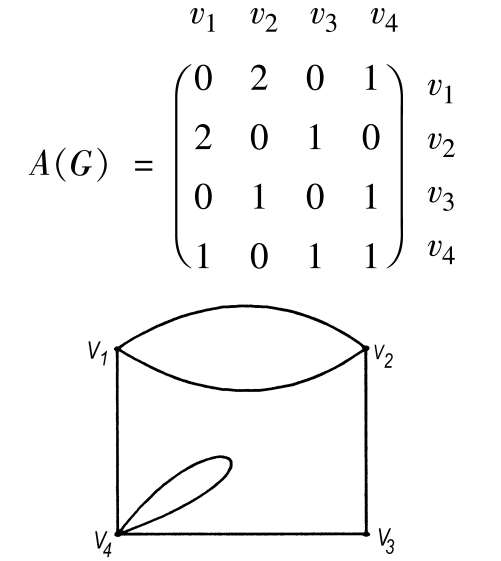
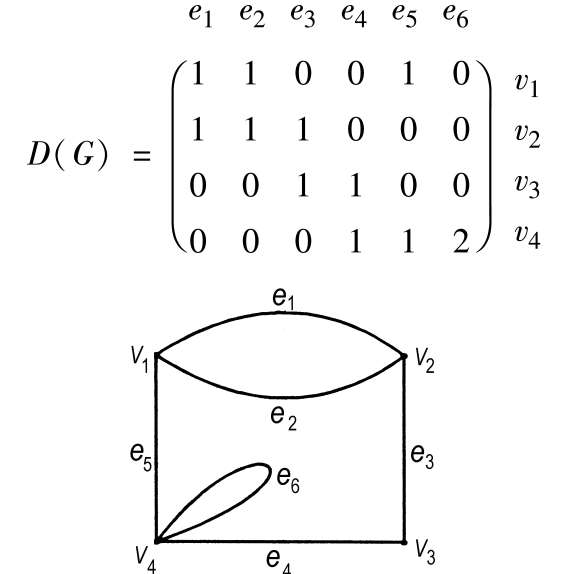
关联矩阵 图的一种矩阵表示。它刻画了图中顶点与边之间的关联关系。设图G的顶点集为
边集为
若n × m矩阵D(G)=(d ij )的元素d ij 是v i 和e j 相联的次数,则称D(G)为图G的关联矩阵。例如,下图的关联矩阵为
图的同构 若两个图G和H的顶点集之间存在一个保持邻接关系的一一对应,则称它们是同构的,记作G≅H。此对应称为同构对应。G与G本身之间的同构对应称为图G的自同构,它是G的顶点集上保持邻接关系的一个置换。
图的自同构群 简单图G的自同构的集合在置换的乘法运算下构成一个群,称为图G的自同构群,记作Γ(G)。它是讨论图的对称性的重要工具。
完美正方形 将一个正方形剖分成边长互不相等的若干个小正方形时,该图形称为“完美正方形”,分成的小正方形的个数称为完美正方形的阶。20 世纪 40 年代发现了完美正方形与电网络理论之间的关系,从而可用图论来研究它,并可用计算机处理完美正方形及类似的完美长方形。如图是一个 21 阶的完美正方形。已经证明,这是阶数最小的唯一的完美正方形。

21 阶完美正方形
哈密顿圈 图论中的著名问题之一。设想一人从图中一点出发,沿着边走,最终回到起点,其间经过图中每个点恰好一次,这种走法亦即这些边的全体称为哈密顿圈。1859 年,英国数学家哈密顿发明了一种绕行世界的游戏,用世界上 20 个著名大城市的名字标在一个正十二面体的 20个顶点上,要求找出沿着边走而经过每个顶点正好一次的走法(如图),哈密顿圈因此而得名。进一步寻找总“距离”最短的哈密顿圈的问题就是流动推销员问题。
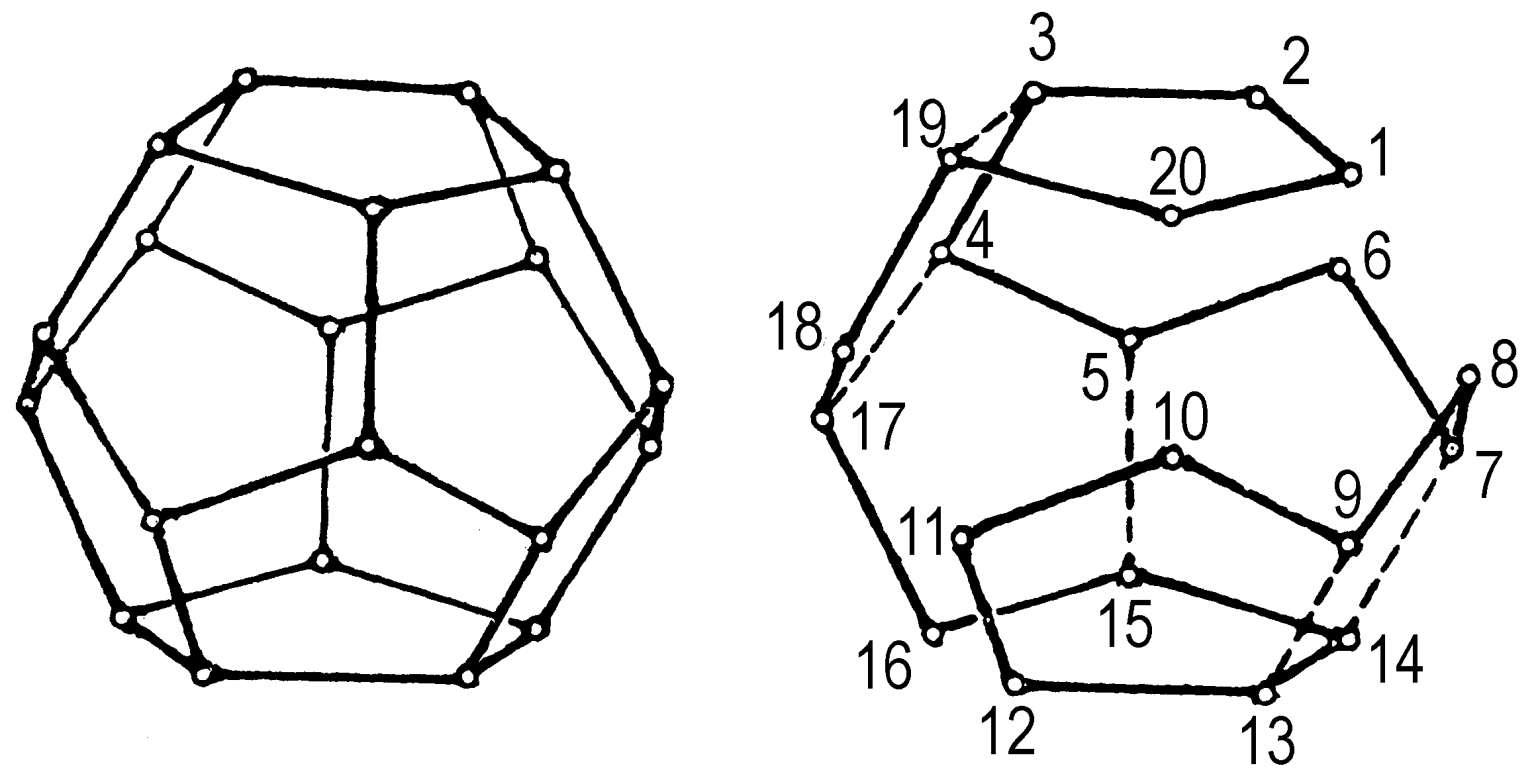
哈密顿圈
七桥问题 古典数学著名问题之一。在哥尼斯堡(今俄罗斯加里宁格勒)的一个公园里,有七座桥将普雷格尔河中的两个岛以及岛与两岸连结起来(如图)。问是否可能从被河流隔开的小块陆地上的任一处出发,恰好通过每一座桥一次,再回到起点。1736 年,瑞士数学家欧拉研究并解决了这一问题,证明上述走法是不可能的。他就此而写的论文是近代图论的发端。参见“欧拉环游”。

哥尼斯堡七桥
欧拉环游 设想一人从图(由一些给定的点及连接这些点的边组成)中一点出发,沿着边走,最终回到起点,其间经过图中每条边恰好一次,这种走法称为欧拉环游,该图称为欧拉图。游戏活动中的“一笔画”问题,就是寻找欧拉环游的问题。参见“七桥问题”。


