中国古算
算数书 中国现存最早的数学著作。是 1983 年底、1984 年初在湖北江陵(今荆州)张家山 274 号汉墓中出土的一批数学竹简,约 190 支完好,因一支有“算数书”三字而得名。存 69 个小标题,100 余条术文或解法,80 余道题目,约三分之二的篇幅是抽象性术文及其例题。绝大多数是秦或先秦完成的。有世界上最早的分数四则运算法则、比例算法、盈不足术、面积体积问题的算法以及若干算术杂题。内容有重复,有的不能自恰,可见是从几部著作撮编而成的。然而它已经具备中国传统数学著作的某些特点。
算经十书 汉唐算经的总集。自汉至唐初的《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《夏侯阳算经》、《张丘建算经》、《缀术》、《五曹算经》、《五经算术》、《缉古算经》等十部算经经李淳风等整理,于唐显庆元年(公元 656 年)颁为国子监算学馆的教材及明算科的考试科目。北宋元丰七年(1084 年)秘书省首次刊刻,时《夏侯阳算经》、《缀术》已佚,前者代之以唐《韩延算术》,后者付之阙如。南宋嘉定年间鲍澣之翻刻时,补入东汉《数术记遗》,仍为十部。清乾隆年间戴震整理之,交孔继涵刻微波榭本,始有《算经十书》之名。后有近人钱宝琮的校点本,今人郭书春、刘钝的点校本。
周髀算经 算经十书之一。二卷。是长期积累编纂而成的数理天文学著作,西汉或更早时期成书。包括商高答周公问、陈子答荣方问等部分,“七衡”以下等八节的内容是陈子所述还是后人补缀,学术界尚无定论。主要以数学方法阐明当时的盖天说和四分历法,使用了相当繁复的分数运算,还有开平方法与勾股定理在中国的最早应用。其“类以合类”的思想,是当时数学的总结,也规范了后来中国传统数学的特点。传本有赵爽注、北周甄鸾述、唐李淳风等注释。
九章算术 一作《九章算经》。算经十书之一。九卷。中国传统数学最重要的著作。其主要内容在先秦已具备,秦火中散坏,经西汉张苍、耿寿昌先后删补而成。分九章:(1)方田——分数四则运算法则与各种面积公式;(2)粟米——以今有术为主体的比例算法;(3)衰分——比例分配算法,以及异乘同除问题;(4)少广——面积与体积的逆运算,最重要的是开平方与开立方法;(5)商功——各种体积公式和土方工程工作量的分配算法;(6 )均输——赋税的合理负担算法,及各种算术难题;(7)盈不足——盈亏类问题算法及其在其他算术问题中的应用;(8 )方程——线性方程组解法与正负数加减法则;(9)勾股——勾股定理、解勾股形及简单测量问题。其主体采取术文统率例题的形式。其中分数理论,比例、盈不足、开方等算法,线性方程组解法,正负数加减法则及解勾股形方法等都是具有世界意义的成就。为《九章算术》作注是中国传统数学著述的重要方式,最著名者有魏刘徽注、唐李淳风等注释、北宋贾宪细草与南宋杨辉详解。其中刘徽注、李淳风等注释与《九章算术》一体行世。已被译成多种文字,是世界古代数学名著之一。
九章算术注 三国魏景元四年(公元263 年)刘徽撰。原十卷,第十卷“重差”系刘徽自撰自注,后以《海岛算经》为名单行。其余九卷与《九章算术》一体行世,既含有刘徽的割圆术、刘徽原理等数学创造,也含有中国传统数学中久已使用,刘徽对之做了发展的出入相补原理、齐同原理、率的理论等内容。它提出了许多数学定义,以演绎逻辑为主要方法全面证明了《九章算术》的算法,是阐释《九章算术》的最重要的著作,奠定了中国传统数学的理论基础,标志着中国传统数学理论体系的形成。
数术记遗 古算书名。一卷。传本题“汉徐岳撰,北周汉中郡守、前司隶、臣甄鸾注”。亦有人认为系甄鸾自撰自注,伪托徐岳。书中记载了亿、兆、京等十个大数及其上、中、下三种进位法。徐岳主张用万万进位的“中数”。还记载了积算、太一算、两仪算、三才算、九宫算、珠算、计数等十四种记数法。其中“积算”即算筹记数法。“珠算”虽不同于后来的珠算盘,开后者之先河,当属无疑。“九宫算”即三阶纵横图。清代以来将其作为《算经十书》的附录。
海岛算经 算经十书之一。一卷,三国魏景元四年(公元 263 年)刘徽撰,本为《九章算术注》之第十卷“重差”,后此卷单行,因第一问为测望一海岛的高、远而得名。现传本共九问,是戴震从《永乐大典》中辑录出来的,都是利用二、三、四次测望所得数据来推算可望而不可及的目标的高、深、广、远。
孙子算经 一作《孙子算术》。算经十书之一。三卷,作者不详,约成书于公元400 年前后。卷上叙述算筹记数制度、筹算乘除法则及各种预备知识。卷中、下都是关于分数运算、衰分、盈不足、商功、线性方程组解法、开平方的应用题。卷下之“河上荡杯”、“鸡兔同笼”问题广泛流传;“物不知数”问题是世界数学著作中首次提出的一次同余式组解法。
缀术 一作《缀述》。汉唐十部算经之一。六卷(一作五卷,或二卷,或数十篇)。南北朝南朝祖冲之(一作祖暅之)撰。隋唐算学馆主要教材之一,是汉唐水平最高的数学著作,因“学官莫能究其深奥,是故废而不理”,遂失传。据《隋书·律历志》与李淳风等《九章算术注释》推测,《缀术》中有精密的圆周率计算,带负系数的二、三次方程解法,以及正确的球体积公式求法等成就。
夏侯阳算经 算经十书之一。原书成于《张丘建算经》之前,北宋刊刻十部算经时已佚,因唐中叶(8 世纪)的《韩延算术》起首有“夏侯阳曰”云云而被误作《夏侯阳算经》刻入,今本即此本之传刻本。三卷。卷上“明乘除法”、“辩度量衡”是预备知识。以下及卷中、下是 82个结合唐代经济、生产、生活实际的应用题。明确使用十进小数,引用当时流传的乘除捷算法,保存了算法改革的一些史料。
张丘建算经 算经十书之一。三卷。清代为避孔子讳改作《张邱建算经》。南北朝北魏清河(今山东临清、河北清河一带)张丘建撰。均为各方面的应用题,在最小公倍数、等差级数、开带从方,以及直接解《九章算术》用盈不足术解决的算术问题上有贡献。卷下之“百鸡”问题是不定方程问题,给出了全部正整数解,在世界数学史上影响深远。
五曹算经 算经十书之一。北周甄鸾撰。是为地方行政人员编写的实用算术书,分田曹、兵曹、集曹、仓曹、金曹五卷,分别是关于田亩面积、军队给养、粟米互换、租税和仓储容积,户调的丝帛和物品交易等问题的计算。内容浅近,避免使用分数。有的题目对十进小数的概念有所发展。
五经算术 算经十书之一。二卷。北周甄鸾撰。对《易》、《诗》、《书》、《周礼》、《仪礼》以及《论语》、《左传》等经籍及其注疏中有关数字计算的地方进行解释,对研究经学有所裨益,然有穿凿附会之处。传本有李淳风等注释。
缉古算经 一作《缉古算术》。算经十书之一。一卷。唐初王孝通撰。其本意是《九章算术》的续篇,共二十题,讨论若干复杂的土方工程及勾股形解法。《缀术》失传后,它是现存中国解数字三次方程的最早著作。
数书九章 古算书名。本名《数术》,亦称《数术大略》、《数学九章》。十八卷(一作九卷)。南宋淳祐七年(1247 年)秦九韶著。分大衍、天时、田域、测望、赋役、钱谷、营建、军旅、市易九类,每类九题,共八十一题。问题之复杂超过以往任何数学著作。其中大衍总数术系统叙述了一次同余式组解法;正负开方术发展了增乘开方法,完整地解决了求高次方程正根的问题;改进了线性方程组解法;其三斜求积公式与海伦公式等价;使用了完整的十进小数记法。还有世界文明史上记载最早的测雨器、量雪器,反映南宋社会经济情况之翔实不亚于《宋史》。
测圆海镜 古算书名。十二卷。1248年元李冶撰。在“洞渊九容”基础上讨论了勾股形与圆的十种基本关系。卷一是本书所需的基本理论,其“圆城图式”用汉字记点,是个创举,“识别杂记”提出六百余条命题,集中国勾股容圆知识之大成。其余各卷就十五个勾股形与同一个圆的相切关系提出了一百七十个求圆径长的问题,大都使用天元术列出一元方程求解,是中国现存最早系统使用天元术的著作,对开方术的发展也有贡献。此外,有完整的十进小数记法。
益古演段 古算书名。三卷。1259 年元李冶撰。北宋数学家蒋周撰《益古集》,都是正方形中有一圆、圆环或长方形,已知其面积求其方边、直径的问题。李冶认为其成就很大,却“閟匿而不尽发”,遂借助于天元术,“移补条段,细繙图式,使粗知百十者便得入室啖其文”。
详解九章算法 古算书名。十二卷。南宋景定二年(1261 年)杨辉以北宋贾宪《黄帝九章算经细草》九卷为底本,撰解题、比类,并在前后分别补充图、乘除、纂类三卷而成。今存约全书的三分之二。公元 11 世纪上半叶贾宪撰《黄帝九章算经细草》,进一步抽象《九章算术》的算法,创造若干新的算法,尤其是贾宪三角和增乘开方法,并补充一些新的题目,是为宋元数学高潮的奠基性著作。杨辉的详解就贾宪的细草而作。在商功章中,以垛积比类多面体体积,发展了沈括的隙积术,提出了几个二阶等差级数求和公式。在纂类中,打破了《九章算术》的分类格局,将《九章算术》的内容按数学方法分成乘除、互换、合率、分率、衰分、叠积、盈不足、方程、勾股九类。
杨辉算法 古算书名。七卷。是杨辉三部著作《乘除通变本末》三卷(1274年)、《田亩比类乘除捷法》二卷(1275年)、《续古摘奇算法》二卷(1275 年)的合集。《乘除通变本末》卷上的“习算纲目”是从启蒙到《九章算术》主要方法的数学教学计划,是数学教育史的重要文献。卷中、下和《田亩比类乘除捷法》总结了民间乘除捷算法与斤两法,有的已与后来的珠算口诀基本相同。《田亩比类乘除捷法》实际上为进一步阐发北宋刘益的《议古根源》而作,保存了刘益的 22 个题目与益积开方术、减从开方术。《续古摘奇算法》对纵横图(即幻方)的研究很有贡献。
算学启蒙 古算书名。三卷。元朱世杰撰,大德三年(1299 年)刊于扬州。全书分为 20 门,259 个问题。卷前列出了 18条学习数学所必需的预备知识以及除法九归歌诀、斤两法等。正文的内容包括了从乘除到增乘开方法、天元术、垛积术等当时数学各方面的知识,形成了一个比较完整的体系。
四元玉鉴 古算书名。三卷。元朱世杰著,大德七年(1303 年)刻于扬州。全书分为 24 门,288 题。卷首有“假令四草”,是天元术、二元术、三元术、四元术的解法模式;深入讨论一元高次方程的解法和多元高次方程组的消元法;形成了高阶等差级数有限项求和问题的完整体系,还有高次招差法等重要成就,其招差公式三百多年后英国的牛顿才研究得出。它是中国传统数学中水平最高的著作。因其内容艰深,清中叶后沈钦裴、罗士琳、戴煦等先后都作过《四元玉鉴细草》,李善兰研究此书有更多的创造。
九章算法比类大全 古算书名。十卷。明景泰元年(1450 年)吴敬撰。沿袭《九章算术》的章名,有一千多个应用题。其中古问源于《详解九章算法》,比类则来自于《海岛算经》、《缉古算经》等古算经及当时的应用题。第十卷专论开方,但不是增乘开方法。是一部筹算与珠算并用的著作。
算学宝鉴 古算书名。四十二卷。明王文素撰,嘉靖元年(1522 年)定稿。依次分成预备知识、方田、粟米、衰分、少广、商功、均输、盈不足、方程、勾股、开方等十一类。其问题大多来自于以前的著作,并通过《九章算法比类大全》引用了《九章算术》的题目。其“通证”、“新证”等项反映了王文素的论证思想,比《九章算法比类大全》严谨。是一部筹算与珠算并用的著作。
算法统宗 古算书名。十七卷,595 问。明万历二十年(1592 年)程大位撰。是明末以后影响最大的以珠算盘为计算工具的数学著作。前二卷是珠算口诀及其在珠算盘上的应用等预备知识,以后各卷的问题大都摘自传本数学书。本书的珠算术以定位、留头乘、归除为重点,编纂上注重基本算法,精讲多练,易学易懂。它适应商业交换的需要,又由徽商带至全国,风行海内,惠及朝鲜、日本与东南亚,对珠算的普及起了极大的作用。
数理精蕴 算书名。五十三卷。清梅瑴成等奉康熙敕令于康熙二十九年(1690年)至六十年编纂,雍正元年(1723 年)刊刻。是康熙年间所编纂的《律历渊源》的第二部分。全面系统地介绍明末以来传入中国的西方数学和当时流行的传统数学。上编五卷“立纲明体”,分别是“数理本源”、“周髀经解”、“几何原本”、“算法原本”。下编四十卷“分条致用”,包括算术运算、开方、勾股、三角、面积、体积等实用算术,以及借根方比例、对数比例、比例规解等代数知识。最后是表八卷,有三角函数、对数等四种表。
则古昔斋算学 丛书名。清李善兰的 13种数学、科学著作的总集。凡二十四卷,1867 年在南京刊刻。其子目为:《方圆阐幽》一卷,《弧矢启秘》二卷,《对数探源》二卷,《垛积比类》四卷,《四元解》二卷,《麟德术解》三卷,《椭圆正术解》二卷,《椭圆新术》一卷,《椭圆拾级》三卷,《火器真诀》一卷,《对数尖锥变法解》一卷,《级数回求》一卷,《天算或问》一卷。前三部及《对数尖锥变法解》研究尖锥术,提出了几个相当于定积分的公式,在接触西方微积分思想之前独立地接近了微积分学。《垛积比类》提出了李善兰恒等式。它沿着中国传统数学的路线接近了高等数学的门槛。
算学 ❶隋唐以后对数学的称谓。隋唐设算学馆,有算学博士,宋有“算学”条例,元朱世杰著《算学启蒙》。宋元起又称为“数学”,此后算学、数学一直并用,直到 20世纪 30 年代。1939 年中国数学名词审定委员会决定用“数学”而废止“算学”。算学遂专指中国传统数学。❷中国古代培养数学人才的学校,亦称为“算学馆”。设于京师。隋隶国子寺,唐、宋隶国子监,元明未设,清隶国子监,后在同文馆亦设算学。隋、唐、宋的算学教材主要是十部算经,即算经十书。
算筹 ❶亦称“筹”、“策”、“筴”、“算”、“算子”。中国古代的计算工具。《老子》云“善数不用筹策”,可知最晚在春秋时已普遍使用。多为竹制小棒,亦有用骨、玉、铁、牙、木等为之者。算筹记数如右图,分纵、横两式。纵横相间,用空位表示零,就可表示任何自然数,亦可表示分数、小数、方程或方程组。❷指耐普尔算筹,明末传入中国。参见“筹算❷”。
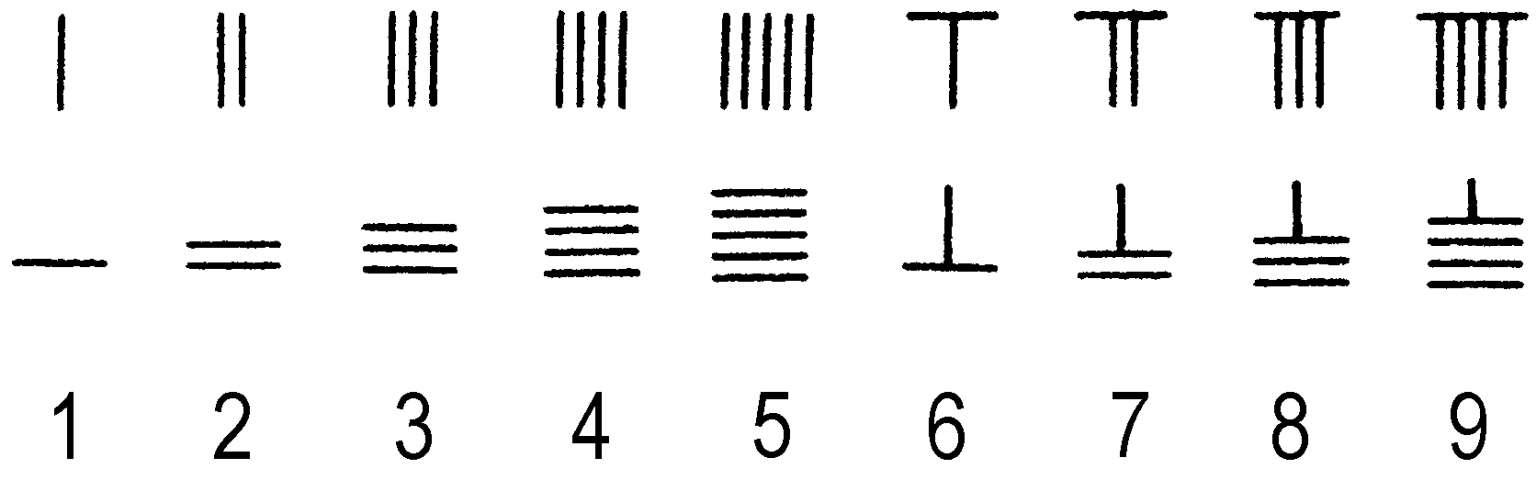
算筹记数
算子 即“算筹❶”。
筹算 ❶中国元明以前以算筹为工具记数、列算式并进行各种运算的方法。中国传统数学的主要成就皆借助于筹算取得。明代逐渐被珠算取代。❷17 世纪初英国数学家耐普尔所发明的一种算筹计算法。算筹用竹或木制成,正反面刻有一至九及其 2 倍至 9 倍的数字以及空筹,如图。明末传入中国,清梅文鼎做了改进。
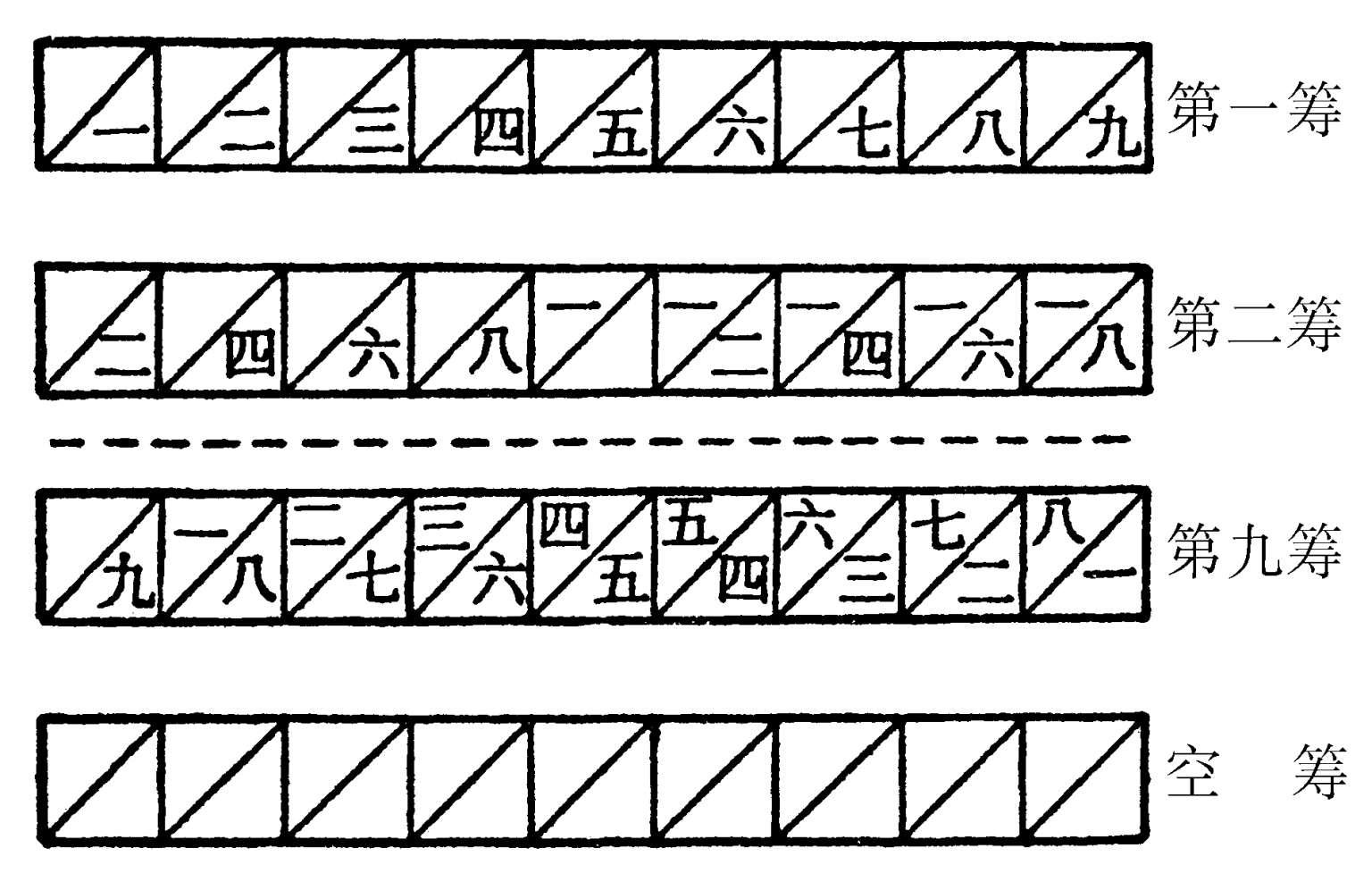
耐普尔算筹
九九 ❶以一至九每两数相乘而成的乘法口诀。古时由“九九八十一”开始,故名。起源甚早,春秋齐桓公设庭燎招贤,视“九九”为“薄能”。元朱世杰《算学启蒙》中有“释九数法”亦指此,然已改为自“一一如一”开始。❷指数学。元李冶病革,语其子曰:“独《测圆海镜》一书虽九九小数,吾常精思致力焉,后世必有知者。”
九数 据《周礼·地官司徒》记载,为当时贵族子弟教育中的数学课程,但未列举其内容。郑玄《周礼注》引郑重曰:“九数:方田、粟米、差分、少广、商功、均输、方程、赢不足、旁要。今有重差、勾股也。”这未必是周初的九数,但最晚在战国时代已有此,并且成为《九章算术》的主体,当属无疑。西汉“差分”改称“衰分”,“旁要”发展为“勾股”。“九数”构成了中国传统数学的主要框架。
方田 九数之一。自汉至清许多中国传统数学著作的重要卷章,解决多边形与曲线形的面积问题。《九章算术》等著作常将分数四则运算法则纳入方田章中。
粟米 九数之一。自汉至清许多中国传统数学著作的重要卷章,解决粟米互换中的数学问题。《九章算术》在粟米章提出今有术。
衰分 亦称“差(cī)分”。九数之一。自汉至清许多中国传统数学著作的重要卷章。《算数书》和《九章算术》提出衰分术,为中国传统数学算法之一,即按已知的比例分配某物的方法。各部分的比例称为列衰。刘徽将其归结为今有术。
少广 九数之一。自汉至清许多中国传统数学著作的重要卷章,主要解决已知面积、体积求其边长的问题,其中在数学上最为重要的是开方问题,发展为中国传统数学的重要分支。
商功 九数之一。自汉至清许多中国传统数学著作的重要卷章,其本意是解决土方工程的工作量分配中的数学问题,然而这必然涉及各种多面体和圆体的体积问题,后者的意义远比前者大,从而成为更重要的内容。
均输 九数之一。自汉至清许多中国传统数学著作的重要卷章。《九章算术》提出均输术,为中国传统数学算法之一。赋税有谷物、徭役之别,各县的户口、距离、价格亦有多少之分,为使缴纳者负担均等而创造此术。用衰分术解决,只是列衰需由各县的条件计算出来。均输术为调节政府和民众、民众之间的关系发挥了有益的作用。
盈不足
亦称“赢不足”。九数之一。自汉至清许多中国传统数学著作的重要卷章。《算数书》和《九章算术》提出盈不足术,为中国传统数学算法之一。典型问题是:今有共买物,人出a
1
,盈b
1
;人出a
2
,不足b
2
;问人数u、物价v各几何?《九章算术》给出的解法是

 刘徽以齐同原理论证了此术的正确性。传入阿拉伯和西方之后,长期成为他们解决数学难题的主要方法。阿拉伯人称之为“契丹算法”,亦称“双设法”。
刘徽以齐同原理论证了此术的正确性。传入阿拉伯和西方之后,长期成为他们解决数学难题的主要方法。阿拉伯人称之为“契丹算法”,亦称“双设法”。
勾股 九数之一。由先秦“旁要”发展而来。自汉至清许多中国传统数学著作的重要卷章,包括勾股定理、解勾股形及简单测望问题。刘徽说在勾股形中“短面曰勾,长面曰股,相与结角曰弦”。
方程 九数之一。自汉至清许多中国传统数学著作的重要卷章,解决今之线性方程组问题。首见于《九章算术》。“方”的本义是并;“程”是求其标准。刘徽说:“群物总杂,各列有数,总言其实。令每行为率,二物者再程,三物者三程,皆如物数程之。并列为行,故谓之方程。”方程按分离系数法和位置值制表示,每行自上而下,各行自右向左排列。其解法称为方程术,中国传统数学算法之一。刘徽以齐同原理证明了直除法的正确性,并提出“举率以相减,不害余数之课”作为其理论基础。刘徽还创造互乘相消法和方程新术。清末李善兰与伟烈亚力,华蘅芳与傅兰雅译西方数学著作,将equation分别译作“方程”与“方程式”。1934 年数学名词委员会确定用“方程(式)”表示equation,用“线性方程组”表示中国古代的方程,最终改变了“方程”的本义。
率 (lü)中国古代指数量之间的一定关系。《九章算术·方田》经分术刘徽注云:“凡数相与者谓之率。”分数的分母与分子、圆的周长与直径等,以至线性方程组的行,都是率关系。刘徽视之为“算之纲纪”。
实 中国传统数学中的被除数,通过“实如法而一”实施除法,“法”是除数。也指方程和线性方程组的常数项。
法 中国传统数学中指除数。也指开方及方程中一次幂的系数。
损益 中国传统数学列线性方程组的方法。《九章算术》方程章曰:“损之曰益,益之曰损。”是说在等式的一端减即在另一端加;在一端加即在另一端减。损益的对象有常数项、未知数,及合并同类项。
今有术
中国传统数学算法之一。《九章算术》粟米章提出:“今有术曰:以所有数乘所求率为实,以所有率为法,实如法而一。”即已知A∶B=a∶b,则
 。《算数书》中已有其应用。刘徽认为今有术是“都术”,《九章算术》的大多数术文和问题的解法,只要找出其中的率关系,应用齐同原理,都可以化为今有术求解。它传入印度和西方后被称为三率法。
。《算数书》中已有其应用。刘徽认为今有术是“都术”,《九章算术》的大多数术文和问题的解法,只要找出其中的率关系,应用齐同原理,都可以化为今有术求解。它传入印度和西方后被称为三率法。
羡除术
《九章算术》提出的求一种复杂楔形体体积的方法。刘徽云:“羡除,实隧道也。”如图。《九章算术》的公式是
 其中
其中
 、l、h分别是羡除的上广、下广、末广、长、高。刘徽将其分割为堑堵及几个鳖臑,求其体积之和证明之。王孝通在《缉古算经》中解决了更复杂的隧道求积问题。
、l、h分别是羡除的上广、下广、末广、长、高。刘徽将其分割为堑堵及几个鳖臑,求其体积之和证明之。王孝通在《缉古算经》中解决了更复杂的隧道求积问题。
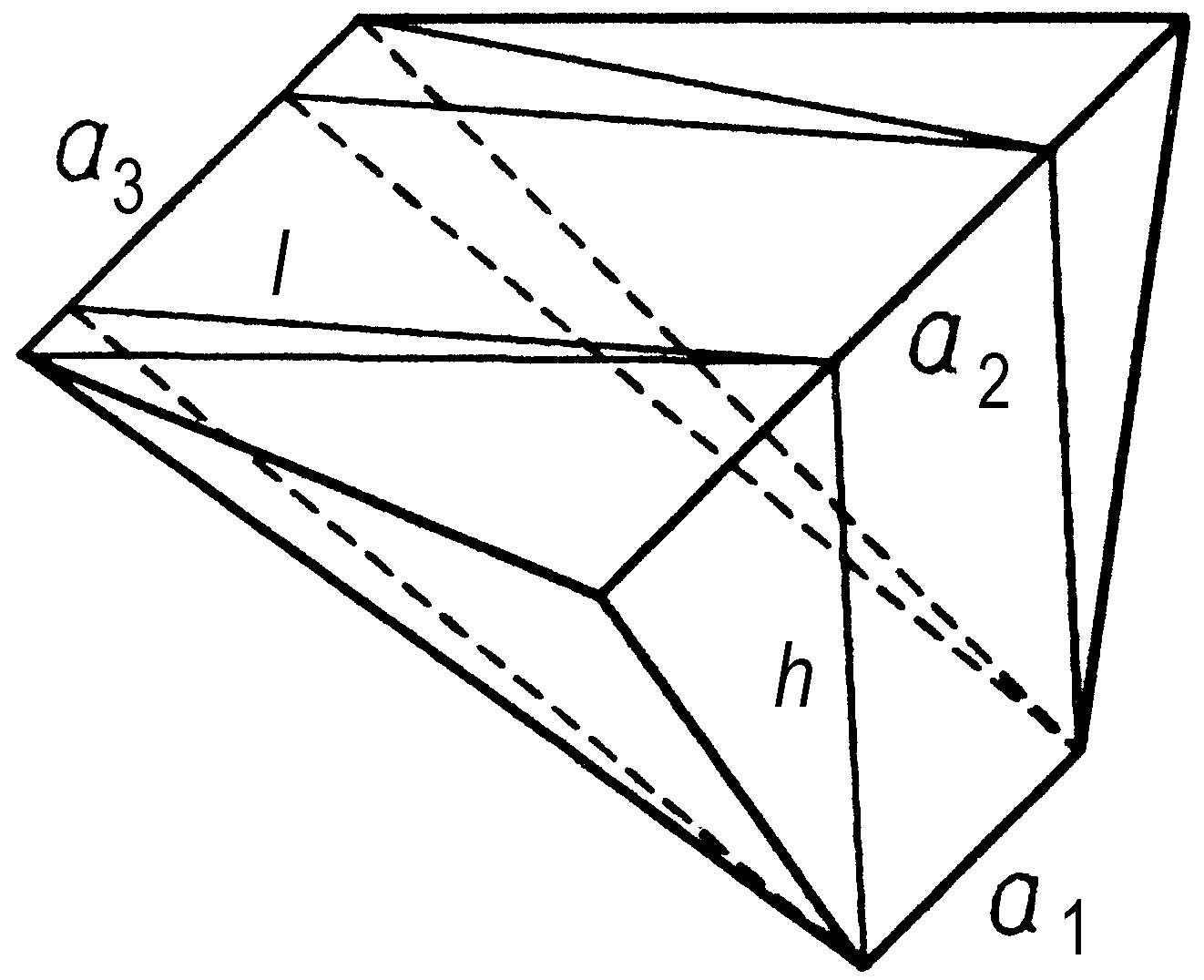
羡 除
正负术 《九章算术》方程章提出的正负数加减法则。“正负术曰:同名相除,异名相益,正无入负之,负无入正之。其异名相除,同名相益,正无入正之,负无入负之。”此即:若a⩾b⩾0,则(±a)± (±b)= ± (a±b),(±a)± (∓b)= ± (a∓b);若b⩾a⩾0,(±a)-(±b)= ∓(b-a),(±a)+ (∓b)= ∓(b-a);若a⩾0,则 0∓(±a)= -a,0 ± (±a)=a。
齐同原理 中国传统数学重要原理之一。源于分数加、减时的通分。刘徽说:“凡母互乘子谓之齐,群母相乘谓之同。同者,相与通同共一母也;齐者,子与母齐,势不可失本数也。”因此,同就是通过各分母相乘得到一个共同的分母,齐就是通过母互乘子保持各分数值不变。刘徽将分数的分子、分母看成率关系,齐同原理自然扩展到整个率的应用中。在衰分术、均输术、盈不足术、方程术等以及各种算术问题中刘徽使用齐同原理进行率的变换,将它们都归结为今有术。刘徽认为,率借助于齐同原理成为“算之纲纪”。
出入相补原理 中国传统数学解决面积、体积和勾股、测望问题所依据的重要原理之一。又称为“以盈补虚”,或“损广补狭”。将平面或立体图形分割成若干部分,再将它们重新拼合成其面积或体积为已知的图形,从而解决与面积、体积有关的问题。它起源于《算数书》、《九章算术》编纂的时代,现传最早的记载在赵爽《周髀算经注》与刘徽《九章算术注》中。它基于这样两个基本的前提:将一个图形分割成若干部分,则它们全体的面积或体积之和等于原图形的面积或体积;将一个图形平移或旋转不改变其面积和体积。
割圆术 用无穷小分割方法和极限思想证明圆面积公式并求圆周率近似值的方法。刘徽在《九章算术》方田章圆田术注中指出,从圆内接正六边形开始割圆,“割之又割,以至于不可割,则与圆周合体而无所失矣”。将与圆周合体的正多边形进行无穷小分割,求其面积之和,从而证明了《九章算术》提出的圆面积等于半周与半径的乘积。借助同样的割圆程序,刘徽分别计算出圆内接正 192 边形、3 072 边形的面积作为圆面积近似值,由圆面积公式反求出周长近似值,从而得到圆周率的两个近似值 157 /50、3 927 /1 250。
微数 刘徽创造的以十进分数逼近无理根的方法。《九章算术》少广章开方术在开方不尽时提出“以面命之”,实际上无法求出其近似值。后来人们“以借算加定法”而命名一个分数,刘徽认为“虽粗相近,不可用也”。他提出“不以面命之”,继续开方,“求其微数。微数无名者以为分子,其一退以十为母,其再退以百为母。退之弥下,其分弥细”,便得出无理根的十进分数近似值。它开十进小数之先河,也是求圆周率精确近似值的计算技术基础。
牟合方盖
刘徽与祖冲之父子解决球体积所使用的模型。为内切于正方体的两个正交圆柱的共同部分,形如两把上下对称的正方形伞(如图)。刘徽认为:“合盖者,方率也,丸(即球)居其中,即圆率也。”因而只要求出牟合方盖的体积,则球体积便迎刃而解。刘徽未能求出其体积,表示“以俟能言者”。后来祖暅之借助祖暅之原理,求出牟合方盖的体积是其外切正方体的三分之二,从而得出球的体积是
 其中d为球直径。
其中d为球直径。
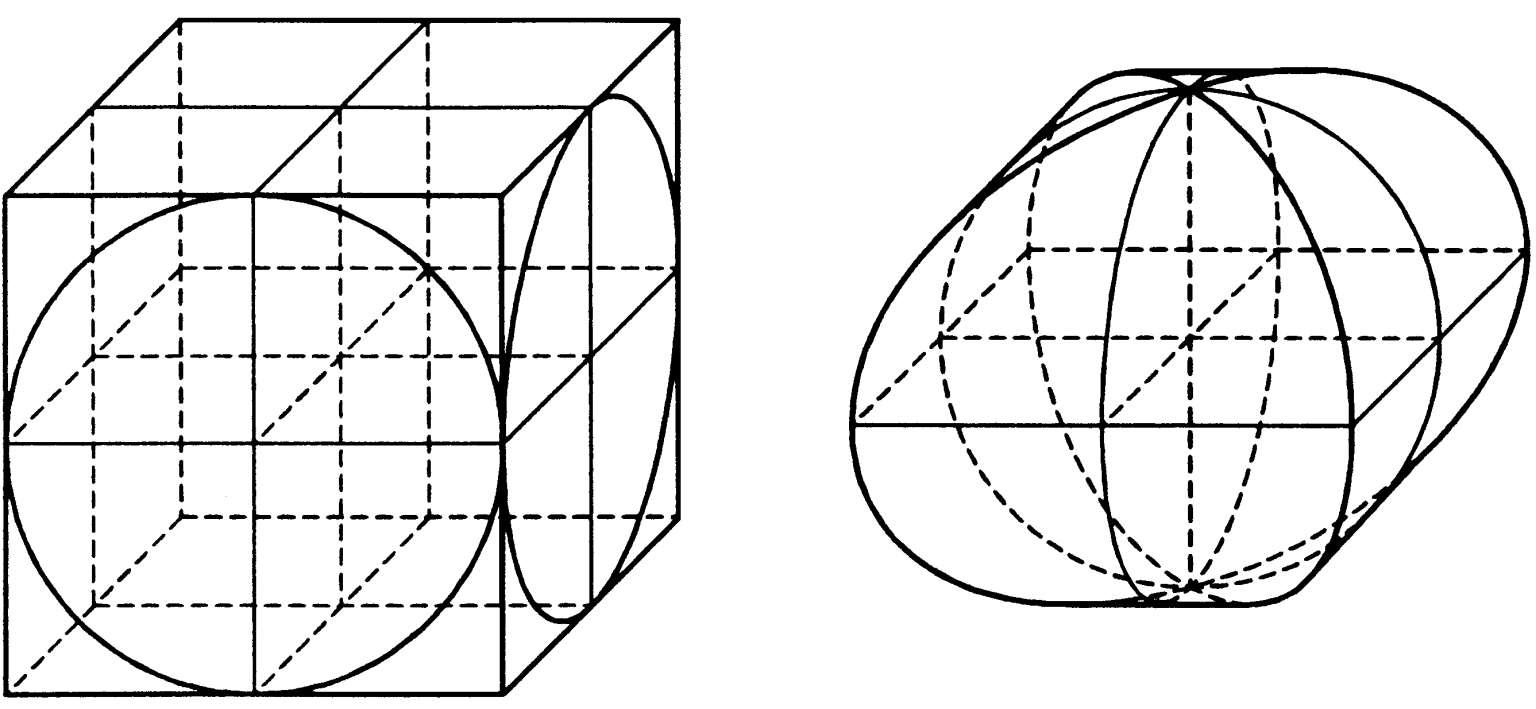
牟合方盖
刘徽原理 中国古代关于多面体体积理论的关键性原理。刘徽认为,多面体都可分解成长方体、堑堵(斜解长方体得二堑堵)、阳马(直角四棱锥)、鳖臑(四面体,斜解堑堵得一阳马一鳖臑)而求其体积。他提出:在堑堵中“阳马居二,鳖臑居一,不易之率也”。并用无穷小分割和极限思想证明了这一原理,进而由堑堵体积是长方体的二分之一,证明了阳马、鳖臑体积分别是长方体的三分之一与六分之一。刘徽进而指出,鳖臑是解决多面体体积的关键,与现代数学的多面体体积理论完全一致。
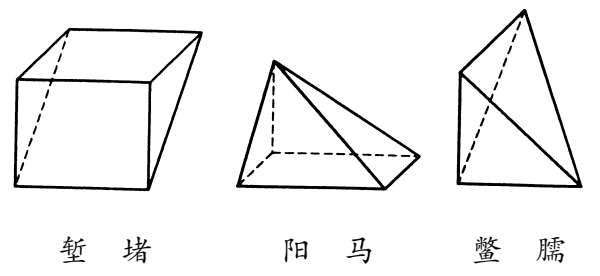
祖暅之原理 亦称“截面积原理”。中国传统数学解决体积问题的重要原理之一。《九章算术》时代已通过比较底面积解决圆体体积。公元 3 世纪刘徽《九章算术注》对此已有理性的认识。公元 5 世纪祖冲之、祖暅之父子在求球体积时指出“幂势既同,则积不容异”,即形状不同的两组立体,只要它们在任意等高处的截面积相等,则它们的体积不能不相等。在西方,该原理由意大利数学家卡瓦列里首先发现,故名“卡瓦列里原理”。
祖率
祖冲之计算出的圆周率精确值。《隋书·律历志》云:对圆周率,“南徐州从事史祖冲之更开密法:以圆径一亿为一丈,圆周盈数三丈一尺四寸一分五厘九毫二秒七忽,朒数三丈一尺四寸一分五厘九毫二秒六忽,正数在盈朒二限之间。密率:圆径一百一十三,圆周三百五十五。约率:圆径七,周二十二。”前者相当于 3.141 592 6 <
 < 3.141 592 7。密率
< 3.141 592 7。密率
 ,是分母小于16 604 的一切分数中最接近圆周率真值的分数。西方直至 16 世纪末德国奥托(V.Otto, 1550—1605 )、荷兰安托尼兹(A.Anthonis, 1527—1607)才求出这个值。
,是分母小于16 604 的一切分数中最接近圆周率真值的分数。西方直至 16 世纪末德国奥托(V.Otto, 1550—1605 )、荷兰安托尼兹(A.Anthonis, 1527—1607)才求出这个值。
重差 中国传统数学的主要测望方法。是从测望太阳的高、远发展起来的。西汉刘安《淮南子》中有重差术的雏形。赵爽《周髀算经注》日高图注和刘徽《海岛算经》中有成熟的重差术,而以后者最为完整、全面。刘徽在《九章算术注序》中指出:“凡望极高,测绝深而兼知其远者必用重差、勾股,则必以重差为率。”总结出重表、连索、累矩三种测望技术。此后,直到明末西方数学传入之前,测望数学在理论上没有大的突破。
纵横图
亦称“幻方”、“魔方”。将从 1到n
2
的自然数排成纵横各有n个数,使每一行、列或对角线上n个数的和均为
 的正方形数表。汉代已有三行的纵横图(如图),称为九宫。南宋杨辉《续古摘奇算法》(1275 年)卷上给出了 3 ~ 10 阶的纵横图造法及其 13 种变体。
的正方形数表。汉代已有三行的纵横图(如图),称为九宫。南宋杨辉《续古摘奇算法》(1275 年)卷上给出了 3 ~ 10 阶的纵横图造法及其 13 种变体。
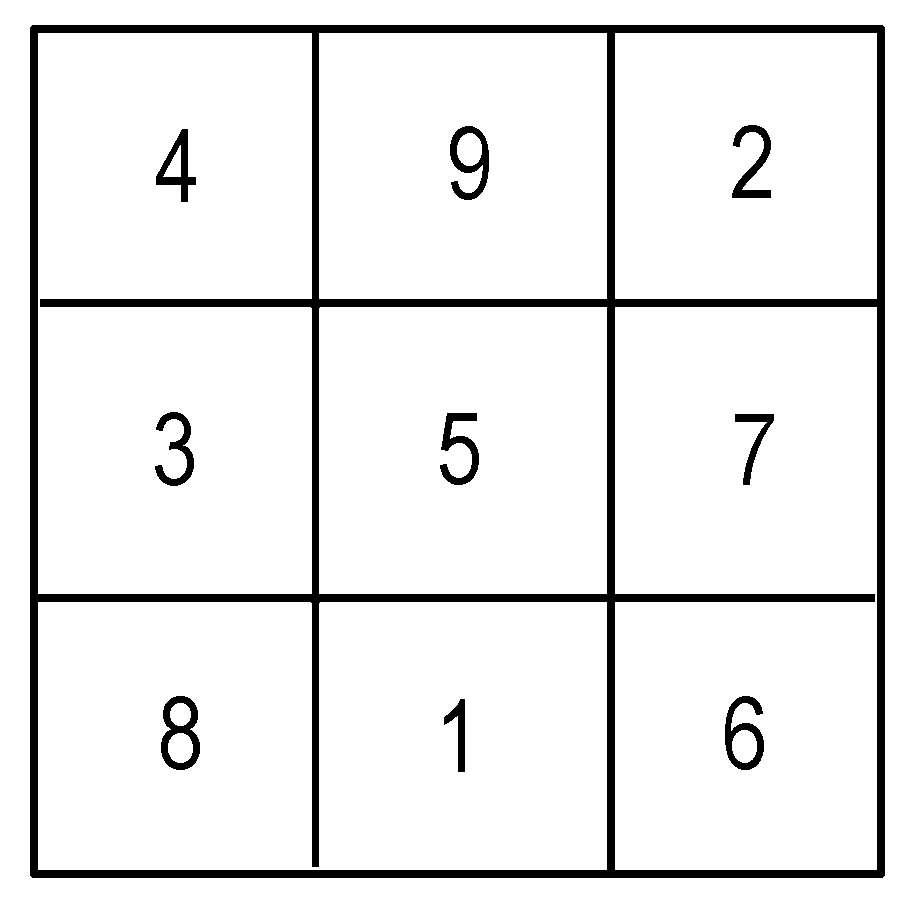
九 宫
幻方 亦称“魔方”。即“纵横图”。
增乘开方法 亦称“递增开方法”。北宋贾宪创造的一种开方法。西方称为“霍纳(W. G. Horner, 1786—1837)法”或“鲁菲尼(P. Ruffini, 1765—1822)-霍纳法”。在求得根的某一位得数后,用随乘随加的方法求减根方程以继续开方,与使用贾宪三角的系数乘平方、立方等异曲同工,而比后者的程序更加整齐,易掌握。秦九韶以此为主导,提出正负开方术,进一步发展为完备的高次方程数值解法。后来在阿拉伯地区,19 世纪初在欧洲也产生了同类的方法。目前中学数学教科书中的综合除法的程序与此类似。
贾宪三角 原称“开方作法本源图”。西方称为“帕斯卡三角”。是将整次幂二项式(a+b) n (n= 0,1,2,3,…)的展开式的系数自上而下摆成的等腰三角形数表(如图)。杨辉《详解九章算法》抄录之,云“贾宪用此术”。当时将开方称为“释锁”,将一些常数列成的算表称为“立成”,贾宪三角就是开方法的“立成”。后来成为朱世杰解决高阶等差级数求和问题的工具。15 世纪阿拉伯数学家阿尔·卡西,16、17世纪欧洲许多数学家都得到同样的三角形。
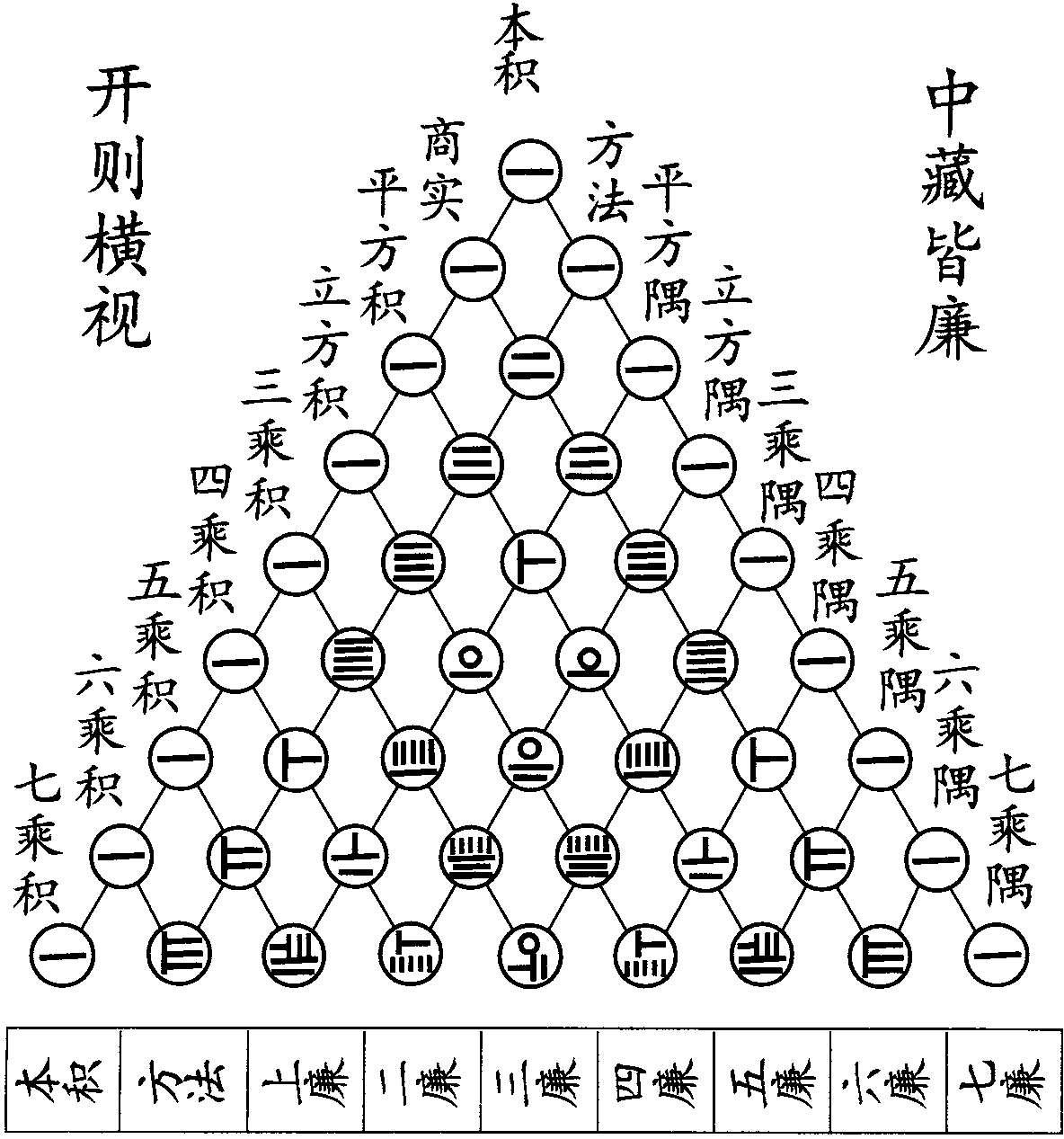
贾宪的“开方作法本源”图
大衍总数术 现代整数论中的一次同余式组解法。《孙子算经》卷下的“物不知数”题是世界数学史上第一个一次同余式组问题,西方称之为“中国剩余定理”。南宋秦九韶在《数书九章》大衍类中系统叙述了这种算法。其核心是大衍求一术,因求乘率的辗转相除程序中须在右上角得一,故名。秦九韶还对实际问题中诸问数不是两两互素的情况提出了化约为两两互素的定数的方法。近代数学大师欧拉、高斯等才达到或超过秦九韶的水平。
三斜求积
秦九韶创造的已知三角形的三边求其面积的方法。设三角形三边小斜a,大斜b,中斜c,秦九韶在《数书九章》中提出了三斜求积术:“以小斜幂并大斜幂,减中斜幂,余半之,自乘于上。以小斜幂乘大斜幂,减上,余,四约之,为实。一为从隅,开平方得积。”此即:
 将根号下多项式分解因式,便知与古希腊海伦公式等价。
将根号下多项式分解因式,便知与古希腊海伦公式等价。
九容 中国传统数学中圆与勾股形的九种相切关系,当时称为“洞渊九容”。宋元时代在《九章算术》勾股容圆术基础上又发展出九种容圆:勾外、股外与弦外容圆,勾股上容圆,勾上、股上与弦上容圆,勾上及弦上容圆半,如图。李冶所著《测圆海镜》即在此十种关系上演绎而成。
天元术 中国古代建立数字高次方程的方法。最早出现约为 12 世纪末,13世纪流行于金、元。《河防通议·算法门》与李冶的《测圆海镜》、《益古演段》是流传至今的最早使用此法的著作。其法先立天元一表示所求的未知数,依据问题所给的条件列出两个等价的含天元的多项式,两者相减,便得到一个一元方程。多项式用分离系数法和位置值制表示:在常数项旁记一“太”字,或在一次项旁记一“元”字,其他项的幂次视与“太”或“元”的相对位置而定。《测圆海镜》及其以前均置高次幂在上,如多项式 2x 3 + 3x 2 -243 表示如图(1);自《益古演段》起改为高次幂在下,如图(2)。
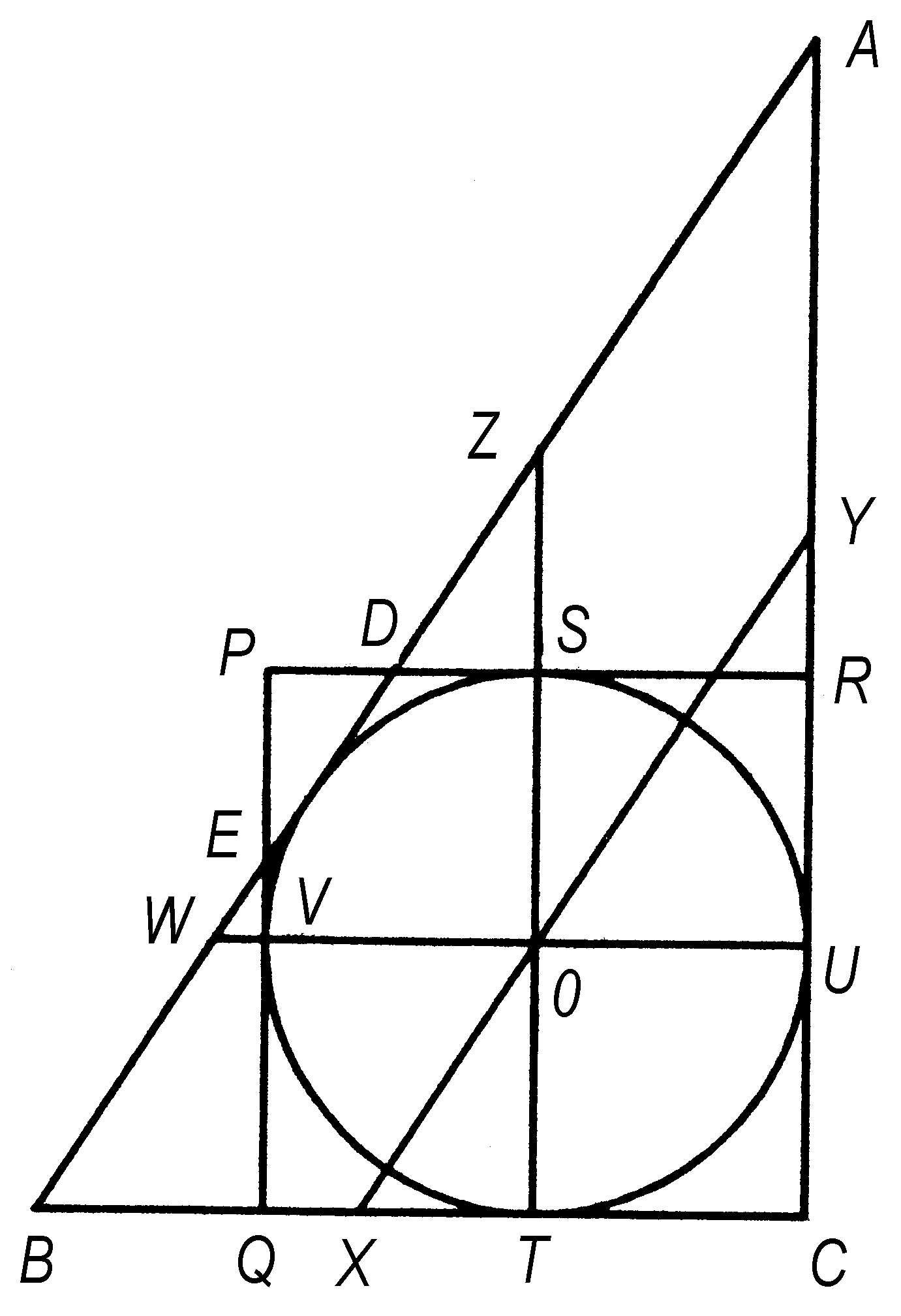
九 容
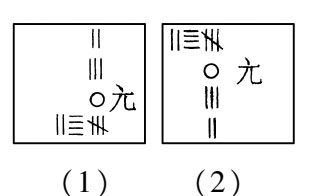
天元术
四元术 中国古代建立多元高次方程组的方法和解法。13 世纪,我国从天元术发展为以天、地二元建立二元高次方程组,以天、地、人三元建立三元高次方程组,最后朱世杰在他的《四元玉鉴》(1303年)里推广到以天、地、人、物四元建立四元高次方程组。四元式的表示法为:常数项居中,旁边记一“太”字,天、地、人、物四元依次居于常数项的下、左、右、上,其幂次视与“太”的相对位置而定。其解法是将四元四式消成三元三式,再消成二元二式,最后消成一元高次方程,用增乘开方法求解。在西方,1779 年裴蜀(EtienneBézout,1730—1783)才研究多元高次方程组的解法。
垛积术 中国传统数学中的高阶等差级数求和法。北宋沈括《梦溪笔谈》卷十八创造的“隙积术”是一个二阶等差级数求和公式。南宋杨辉在《详解九章算法》改称“垛积术”。元朱世杰在《算学启蒙》、《四元玉鉴》中的垛积术解决了任意高阶等差级数的有限项求和问题,形成了完整的系统。
招差术 即如今的内插法,亦即“有限差分法”。中国古代用于历法计算和垛积计算。隋刘焯编制《皇极历》时(公元 600年)已用到二次差。元王恂、郭守敬的《授时历》已用到三次差。朱世杰《四元玉鉴》将高阶等差级数求和的知识用于解决高次招差问题,提出了四次招差公式,并可以写出任意次差的公式。西方同样的公式是牛顿在 1676 年创造的。
尖锥术
清李善兰创造的求定积分的方法。他在《方圆阐幽》(1845 年)中提出:“当知诸乘方皆可变为面,并皆可变为线。”即若x为任意正数,n为正整数,则x
n
的数值可以表示成一个平面积,也可以表示成一条直线段。进而指出,“当知诸乘方皆有尖锥”,“当知诸尖锥有积叠之理”。即当x在区间[0,h]内时,表示x
n
的平面积叠成一个尖锥体。他得出诸尖锥的算法:由平面积ax
n
积叠起来的尖锥体,高为h,底面积为ah
n
,其体积为
 ,此命题相当于定积分
,此命题相当于定积分
 。他还提出了其他相当于定积分的结果,都是在中国传统数学基础上独立完成的创造性工作。
。他还提出了其他相当于定积分的结果,都是在中国传统数学基础上独立完成的创造性工作。
借根方 清初传入的西方设未知数列方程的方法。《数理精蕴》下编卷三十一云:“借根方者,假借根数、方数以求实数之法也。”“根数”就是未知数,“方数”就是根数的正指数幂。中国 13 世纪发展起来的天元术、四元术,明代及清初无人通晓。梅瑴成学得借根方法后,“窃疑天元一之术颇与相似。复取《授时历草》观之,乃涣如冰释”,从而理解了天元术与四元术。
百鸡术 中国古代著名的不定方程问题,见之于《张丘建算经》卷下第三十八题:“今有鸡翁一直钱五,鸡母一直钱三,鸡雏三直钱一,凡百钱买鸡百只。问鸡翁、母、雏各几何?”张丘建给出了(4,18,78),(8,11,81),(12,4,84)三组解,是其全部正整数解。其解法是:“术曰:鸡翁每增四,鸡母每减七,鸡雏每益三,即得。”13世纪意大利斐波纳奇、15 世纪阿拉伯阿尔·卡西的著作中也出现了同类问题。
鸡兔同笼 中国古代著名的趣味算题。见之于《孙子算经》卷下第三十一题:“今有雉、兔同笼,上有三十五头,下九十四足。问雉、兔各几何?”雉即野鸡。其解法思路是:鸡 1 头 2 足,兔 1 头 4 足。半其总足数,头数不变,则 1 鸡为 1 头 1 足,1 兔为 1 头 2 足。1 兔比1 鸡多 1 足,故总足数之半比头数所多之数即兔数;总头数减兔数即鸡数。此题流传日本等国,闻名于世。
珠算 运用算盘进行加、减、乘、除、开方等计算的方法。最先见之于《数术记遗》,是中国最早用滚珠在盘上计算的记载。但珠不穿档,不是元、明后的珠算。宋、元时人们创造的乘除捷算法促进了筹算向珠算的演变,筹算口诀亦变成珠算口诀,便于记诵,算法简捷,运算迅速。明代已盛行,后来流传至东亚各国。
算盘 中国传统计算工具之一。其雏形首见之于东汉徐岳《数术记遗》的太一算、两仪算、三才算、珠算等记数法与计算法中,当时称为算板。南宋刘胜年所绘《茗园赌市图》、元至大三年(1310 年)所绘《乾坤一担图》中都有算盘图,知它在当时已经流行。现存算盘图式始见于明《魁本对相四言》(1371 年)。其形长方,周为木框,内穿档,档中横以梁。梁上二珠或一珠,每珠作数五;梁下五珠或四珠,每珠作数一。定位后利用口诀拨珠计算。因其口诀易诵,简单易学,运算简捷,且便于携带,元明后逐步取代算筹成为主要计算工具,并流传于朝鲜、日本和东南亚各国。
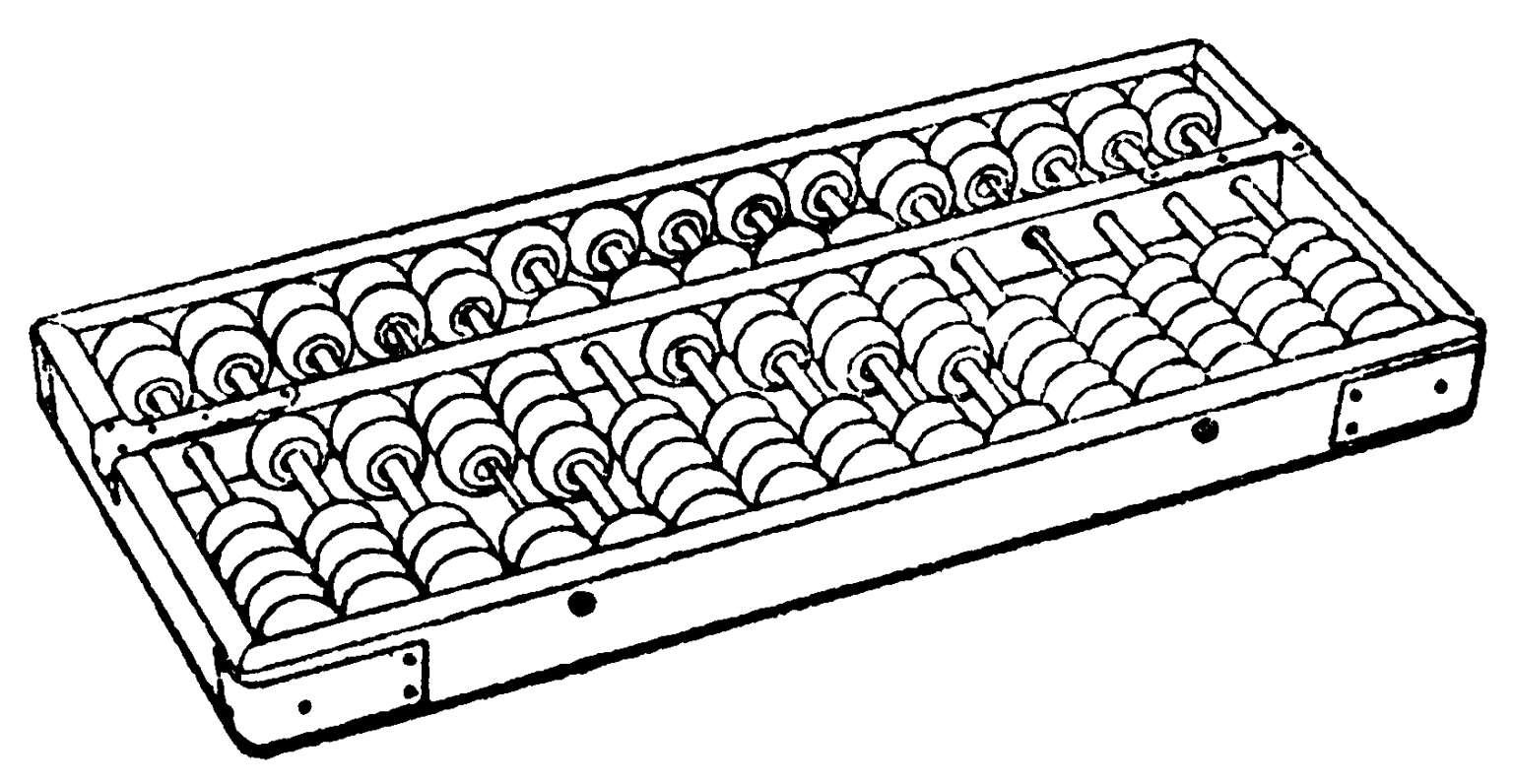
算 盘
斤两法 俗称“流法歌”。筹算和珠算中中国旧制斤与两(一斤等于十六两)的换算方法,有“斤求两”和“两求斤”两种。前者用十六的倍数编成口诀:“斤如求两身加六”。如 2 斤化为两,则以 6 的 2 倍加上 20,得 32 两。后者的口诀:“减六留身两见斤”。如 32 两化为斤,就从 32 两中减去 6 的 2 倍,即得 2 斤。还有将两化为斤的小数的口诀,如“五,三一二五”就是 5两= 0.312 5 斤。斤两法的口诀最早见于杨辉《乘除通变本末》与朱世杰《算学启蒙》中。1959 年 6 月 25 日国务院颁布斤两改为十进制后,无须再用此法。
流法歌 “斤两法”的俗称。
留头乘 亦称“穿心乘”。元代创造的三位以上的乘数的一种乘法方式,因将乘数首位留至最后再与被乘数相乘而得名。起于筹算,用于珠算,初见于元朱世杰《算学启蒙》。其法先从乘数左起第二位起至未位,依次向右乘被乘数,再以乘数首位乘;先乘被乘数的个位,再乘其十位、百位等数。如 563 × 874,计算的顺序是:3 ×70,3 × 4,3 × 800;60 × 70,60 × 4,60 × 800;500 × 70,500 × 4,500 × 800。
归除 元明时期创造的除数在二位以上时的除法算法,起于筹算,后来用于珠算。除数是一位的除法称“归”,除数是二位或二位以上的除法就称“归除”。它是在九归与减法基础上发展起来的。如除数是 385,就称为三归八五除。其法以除数首位对齐被除数首位,通过九归口诀,得出商数。随即将商数与除数首位以后各数的乘积,从被除数中减去,如是逐位进行,直至被除数减尽或商数满足要求的位数为止。运用归除可不经估计而直接求得商数。
九归 从 1 至 9 的一位除数的除法口诀。原由筹算产生,杨辉《乘除通变本末》、朱世杰《算学启蒙》先后总结。明代柯尚迁、程大位等稍加增删,用于珠算。归是一位除法。如朱世杰的三归口诀“三一三十一”就是 10 除以 3 商 3 余 1。六归口诀“六一下加四”就是 10 除以 6 商 1 余4,其中第二个“一”既是被除数,又是商数;“逢六进一”就是 6 除以 6,商 1,口诀中省略除数 6。
飞归 亦称“飞除”、“穿除”。宋元时期创造的一种简捷除法,起于筹算,后用于珠算。初见于南宋杨辉《乘除通变本末》。它将归、除合并,编成口诀,归后不用商除,以简化运算程序。如“一归二除”的口诀“见一加七隔加四”,即以 1 加 7,商数为8;商数 8 之下隔一位加 4。因以 12 除100,商 8,以 8 乘 12 得 96,减 100 余 4。用法是将被除数打在算盘上,从左起逐位呼诀运算。除数的位数不受限制,均可编成飞归口诀。运算程序简便,但口诀繁琐。
撞归起一 元代创造的归除中的一种运算方法。起于筹算,用于珠算。被除数与除数首位相同,而商数与除数首位之下各数乘积大于被除数首位之下的数值,须用此法。元末丁巨《丁巨算法》、贾亨《算法全能集》的筹算口诀与现今的珠算口诀基本相同。30 ÷ 34,口诀为“见三无除作九三”,商为 0.9,尚余 3。除数 4 乘 0.9 为3.6,减余数 3,不足减,须用起一法。口诀为“起一下还三”,得商数为 0.8,余数 6。除数 4 乘 0.8 为 3.2,从余数 6 中减去,余数 2.8。


