2.3 实际的电容
相对于电阻而言,电容更复杂,通常需要考虑容值、耐压、精度、材质。不同作用的电容,材质也有很大的区别。对于初学者来说,容易忘记电容的耐压和材质问题。
2.3.1 电容的参数以及影响
电容最基本的公式就是充放电公式: Q = CU ,式中, Q 是电容存储的电荷量(C), C 是电容的容值(F), U 是电容两端的电压(V)。电容存储的电荷量 Q = It ,式中, I 是流入电容的电流(A), t 是充电时间(s)。
在ATE的测试电路中,如果使用电容滤波,那么必须考虑电容的充电和放电时间。比如电容容量为10μF,电压需要从0V充电到5V,采用的电流档位为10mA,那么在电容充电时刻,相当于恒流向电容充电。这时, t = C · U / I =10μF×5V/10mA=5ms,也就是需要至少5ms的时间,电容两端的电压才能达到设置值。在IC测试中,在设置了测试条件之后,通常需要一段稳定时间,延时之后才能执行测量。这些延时时间除了IC自身的响应时间外,其他大多数情况下,与外部电路的电容的充放电时间有关。建议使用外部示波器或者ATE自带的示波器查看确认开始测量之前IC是否工作在稳定的状态,避免测试到错误的结果或者不稳定的结果。
电容的精度通常要求都不高,但是某些IC,比如常见的开关电源IC,可能使用电容的充放电时间作为定时来设置工作频率,那么测试频率的结果就会与电容精度相关。这时必须要使用LCR数字电桥来测量电容的容值。但在普通退耦电路中,则没有必要测量电容的容值。
有很多IC在实验室阶段需要进行高低温(低温、常温、高温)测试。这些IC有的要求电容必须靠近引脚才能正常工作。这时候,选择电容就必须满足测试的温度范围的要求,否则会影响测试结果。
目前在开关电源IC中,内置MOS器件比较常见,在测试中会有施加高压测量漏电流或者施加指定的电流测量耐压,这些都涉及高压测试。高压测试的电流通常都不大,这时线路中的电容干扰会比较明显,因此需要等待高压稳定之后,才可以测量漏电,或者测量耐压。由于IC封装后无法确定内部的情形,因此,高压测试时,各个引脚连接的电容,必须满足最大的耐压需求,避免IC内部短路造成其他引脚的电容损坏。
2.3.2 实际电路中的电容
实际的电容除了容值、耐压、温度系数等,还需要考虑材质、等效串联电阻(Equivalent Series Resistance,ESR)、损耗因数、漏电流等。
这里仿真一个开关电源的电路,电容的ESR影响输出电压的仿真如图2.3.1所示。一个恒流400mA的电流源向电容充电,连接2Ω的负载,将C1的10μF电容设置ESR为500mΩ。仿真电路里有使用开关,LTspice支持Voltage Controlled Switch,也支持Current Controlled Switch。这里使用的是电压控制型开关,具体可以查看LTspice的文档(在LTspice界面按F1快捷键即可打开帮助文档Help Topics)。
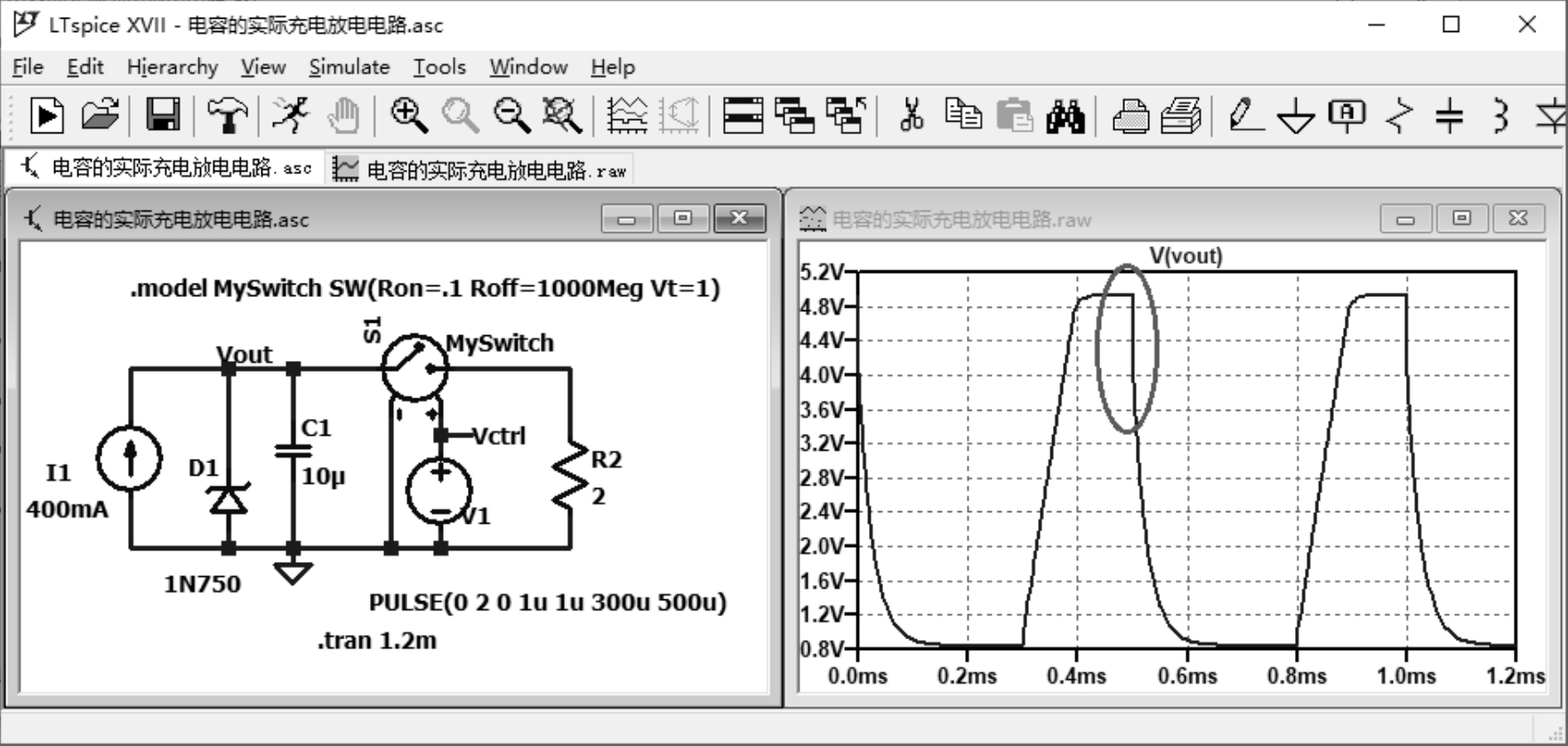
图2.3.1 电容的ESR影响输出电压的仿真
注意图2.3.1所示的仿真结果中,在放电的瞬间,电压是直接跌落,而不是呈指数下降,与理想的放电曲线不符合。实际上,因为电容内部存在ESR,当负载电阻很小,数量级与ESR相当时,就能在电容放电时看到这一现象。在放电的瞬间,ESR和负载电阻构成了分压电路,所以电压瞬间跌落,而不是指数下降。某些时候,电容的ESR会影响到最终的测量结果。
有些测试条件中没有提到电容,但是实际电路中还是需要一些退耦电容或者补偿电容。由于测试线路通常需要连接比较长的连线,长导线的寄生等效电容较大,就等效连接了一个较大的负载电容。这些等效电容非常容易形成振荡或者振铃效应。
这里仿真一个缓冲器,连接电容负载,缓冲器连接电容负载的振铃效应如图2.3.2所示。当运放的输出电流越大,输出摆率越高时,越容易引发振铃效应。
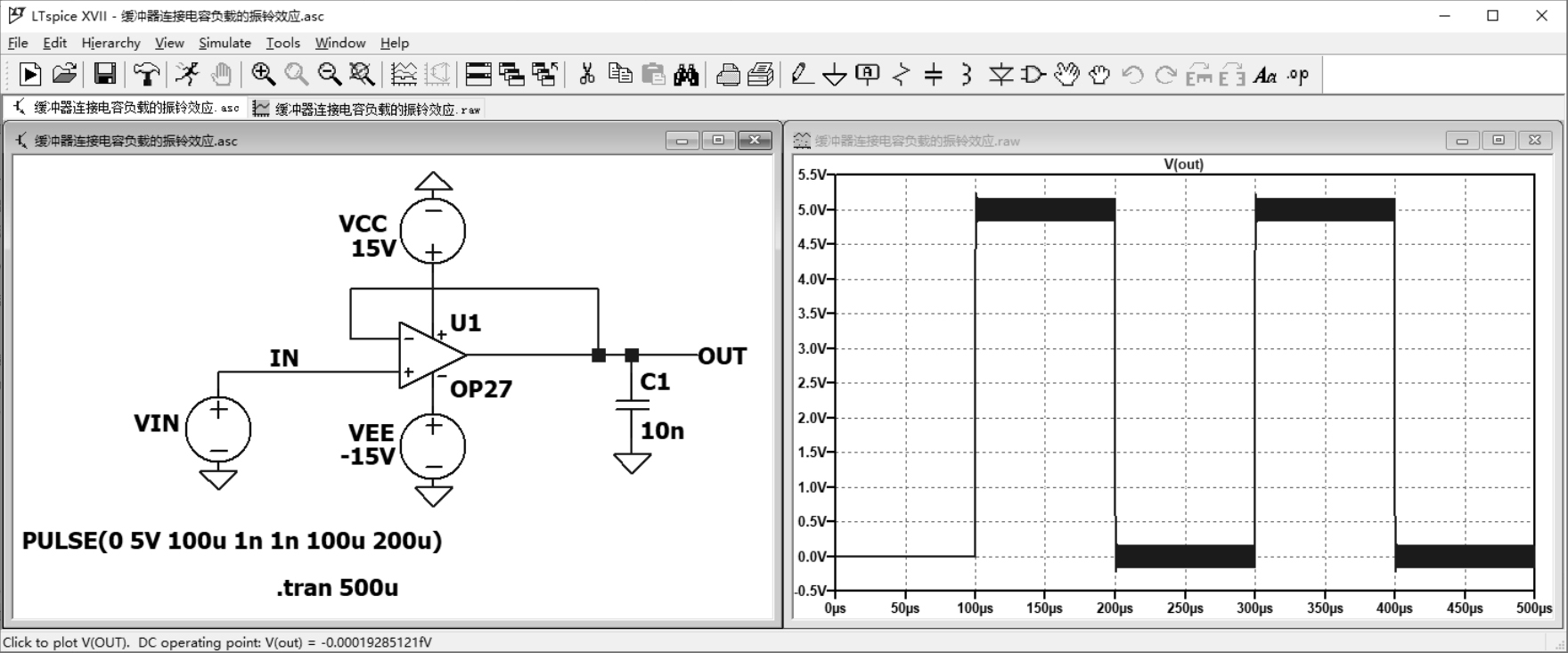
图2.3.2 缓冲器连接电容负载的振铃效应
这里仿真的运放输出摆率不够快,因此加大了负载电容。某些运放,几皮法的电容就足以引发振荡。所以通常需要在运放的电源端加退耦电容,并且在输出端串联隔离电阻来抑制振铃效应,缓冲器增加隔离电阻抑制振铃效应如图2.3.3所示。
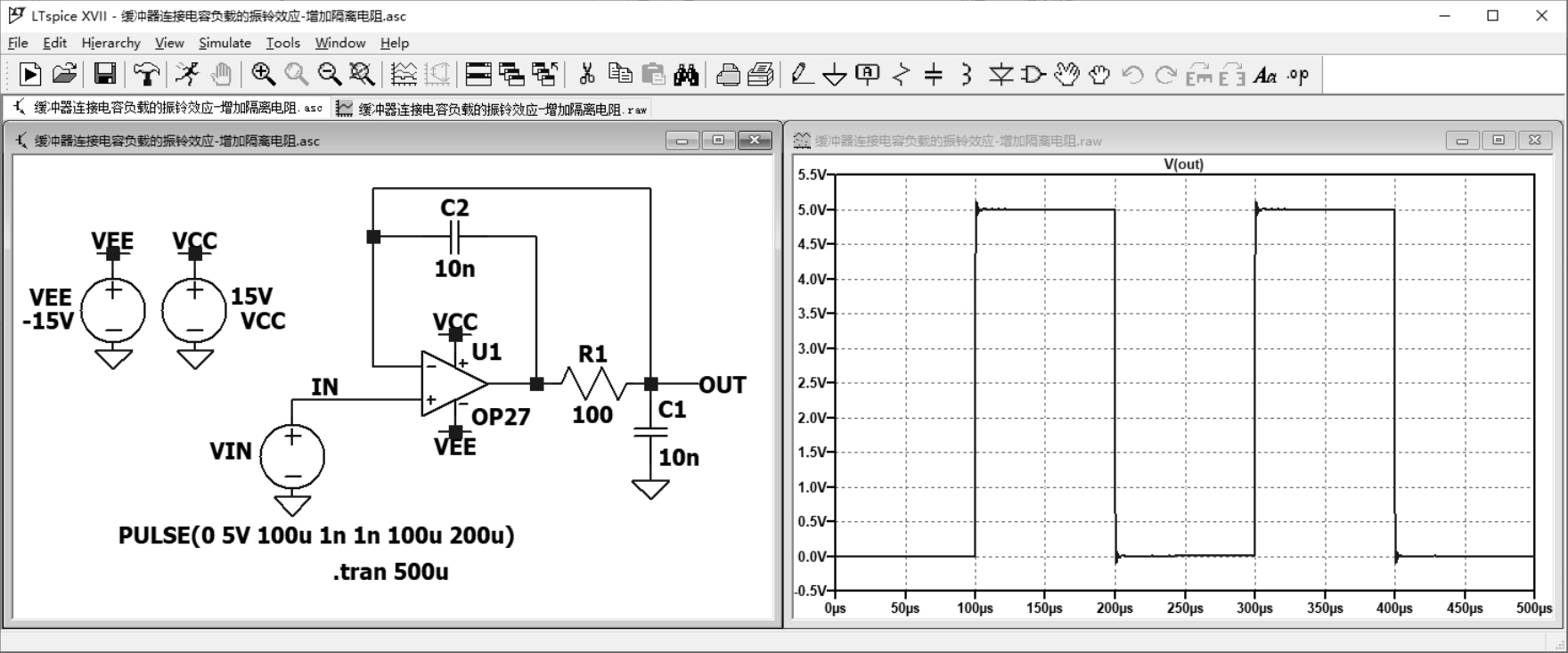
图2.3.3 缓冲器增加隔离电阻抑制振铃效应
流过电容的电流可以瞬间变化很大,而电容两端的电压不会瞬间变化很大。这就导致了电路交流通路和直流通路的不同。比如1mV/10kHz的正弦信号(模拟纹波干扰)叠加在5V的直流通路上,负载是10kΩ的电阻并联10μF的电容,电容对纹波电流的影响的仿真电路及仿真结果如图2.3.4所示。
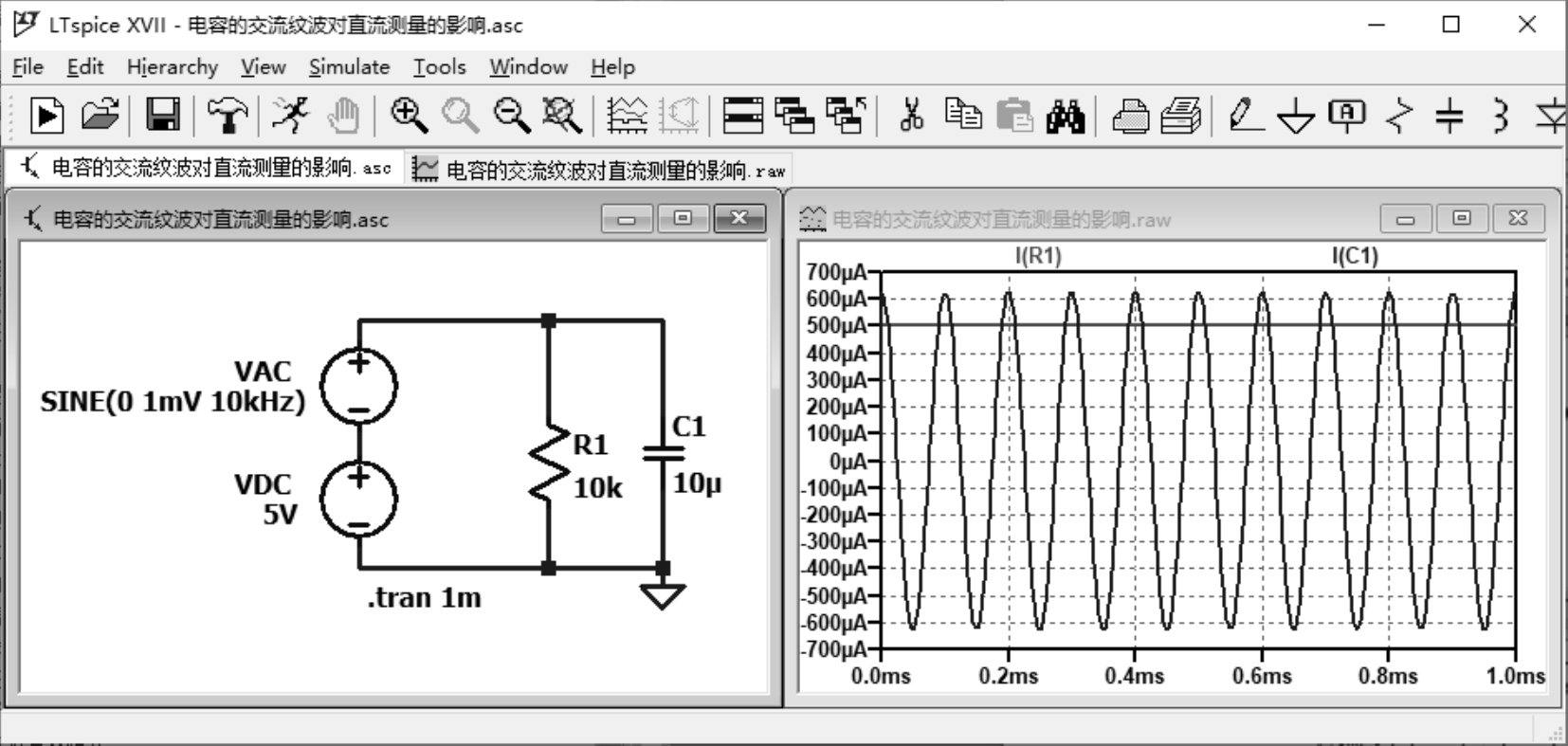
图2.3.4 电容对纹波电流的影响仿真电路和仿真结果
从仿真结果可以看到,电容上的电流与电阻上的电流差异很大。电阻上的直流电流为5V/10kΩ=500μA,纹波电流为1mV/10kΩ=100nA(约为直流电流的0.02%,可以忽略不计),而电容上则直流电流为0A,纹波电流为1mV/(1/(2×π×10kHz×10μF))=628μA。
从源端来看,输出电流在500μA±628μA之间波动,如果测量的采样率大于10kHz,那么执行单次测量,数据的波动全距(最大值-最小值)就会达到2倍的电容纹波电流。但如果测量时间是一个纹波的周期,那么平均下来就只有直流电流了。所以ATE一般对于存在纹波干扰的测试,可以执行纹波周期整数倍的时间测量,通过计算平均值来消除纹波的干扰,也就是数字信号处理中的均值滤波。
电容除了交流电流以外,直流的情况下也存在微小的漏电流,漏电流计算公式为 I = kCU ,式中, I 是电流(A), k 是系数, C 是电容容量(F), U 是电容的额定电压(V)。某些情况下,直流漏电流也会对测试结果造成比较明显的误差。一般高压漏电测试,都不允许在引脚处连接电容,一方面影响高压上升的速度,另一方面就是电容本身存在直流漏电流。测试电路通常会使用继电器来控制大电容的连接。这里特别需要注意一点,大容量电容(μF级别以上的容量)通常储存的电荷量比较大,因此通常需要额外的电路进行放电。一般情况下使用单刀双掷继电器,当电容不连接到电路时,可以连接一个电阻到地线进行放电。
在测试电路中,因为每个DUT是连续测试的,要确保每个DUT进入测试电路时,测试电路的状态都是相同的,所以,特别需要注意电容元件的储能的影响,电容电路一定要有放电通路。
最后简单说明一下电容材质问题,在使用电容时,可以在网络上搜索所需要的功能对应的电容材质。比如滤波电路在不同的频率范围,不同的耐压范围,有不同的电容材质可以选择,如多层陶瓷电容、铝电解电容、钽电容、独石电容、薄膜电容、涤纶电容等。
2.3.3 电压驱动电阻电容( RC )电路的一阶系统响应
在信号完整性分析中,可能会遇到公式:

式中, f w 是-3dB带宽(Hz), t r 是10%~90%的信号上升沿时间(s)。
这个公式的推导可以用电压驱动电阻电容(Resistor-Capacitance, RC )电路的一阶系统响应来分析。电压驱动 RC 电路一阶系统响应如图2.3.5所示。
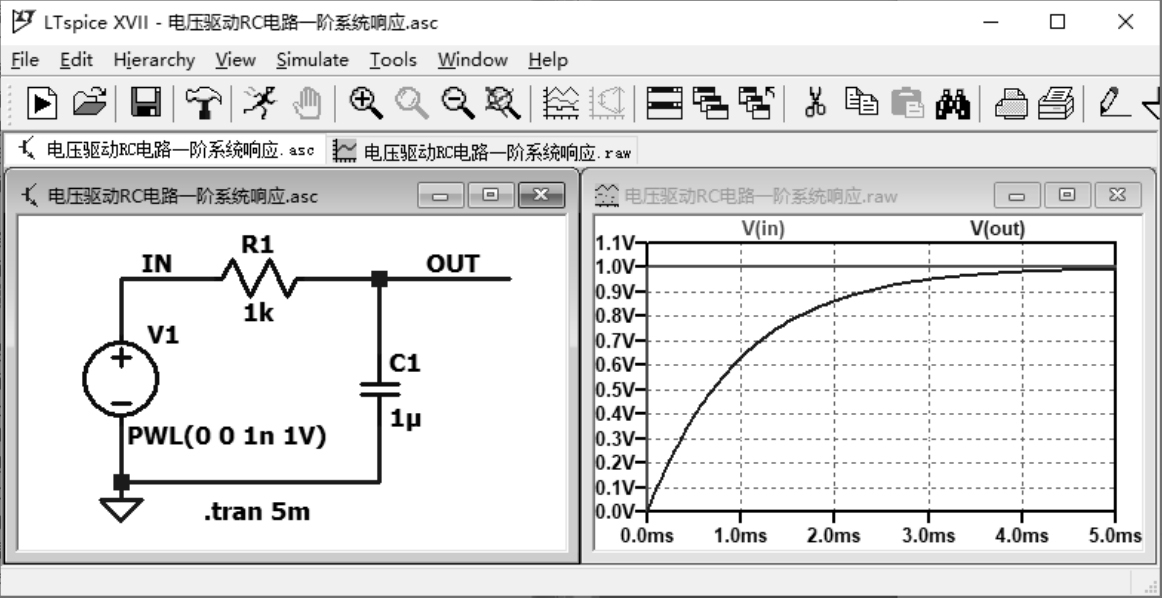
图2.3.5 电压驱动 RC 电路的一阶系统响应
电容的充电电压公式为:

式中, V ( t )是电容电压对时间的函数, V s 是电源电压(V), t 是电容加上电源电压之后的任意时刻对应时间(s), R 表示电阻的阻值, C 表示电容的容值。假设10%的上升时间为 t 1 ,90%的上升时间为 t 2 ,可以建立方程:

联立方程,可以得到:
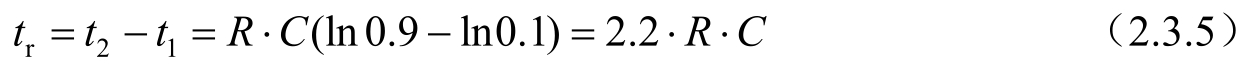
利用一阶系统的传递函数,可以计算出-3dB的带宽。这里为了方便理解,从时域上进行分析。
RC
构成低通滤波电路,-3dB带宽就是输出电压下降到70.7%(1/
 )的频率点。假设输入一个幅值为1的正弦信号,那么输出的幅值为
V
out
=
V
in
Z
c
/(
Z
r
+
Z
c
),式中,
Z
r
是电阻阻抗(Ω),
Z
c
是电容阻抗(Ω)。
V
out
的幅值为
V
in
的幅值的70.7%时的频率值就是-3dB带宽。
)的频率点。假设输入一个幅值为1的正弦信号,那么输出的幅值为
V
out
=
V
in
Z
c
/(
Z
r
+
Z
c
),式中,
Z
r
是电阻阻抗(Ω),
Z
c
是电容阻抗(Ω)。
V
out
的幅值为
V
in
的幅值的70.7%时的频率值就是-3dB带宽。
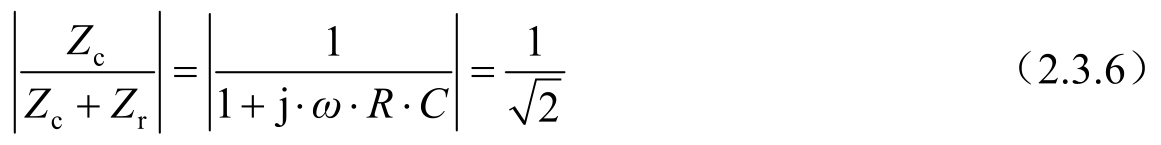
ω
是正弦信号的角频率;
f
是正弦信号的频率
ω
=2π·
f
。由式2.3.6求出
ω
·
R
·
C
=1,j是工程上的虚数符号j=
 。这里求出的
f
就是-3dB带宽即
f
w
=
f
。可以导出:
ωRC
=1,即2π
fRC
=1,
。这里求出的
f
就是-3dB带宽即
f
w
=
f
。可以导出:
ωRC
=1,即2π
fRC
=1,
 。
。
这个是一阶电压驱动 RC 系统的响应,如果利用方波的傅里叶变换计算信号的上升沿和带宽的关系,也同样可以拟合出该等式。这个带宽是电路的小信号带宽,也可以认为是线路传输过程中的截止信号带宽。这里留一个问题,100MHz的带宽,能否通过100MHz的方波信号?通过之后的信号波形是什么样子的?


