2.3 传输线耦合理论
众所周知，在射频微波电路中，基于双导体或多导体耦合结构的各种形式的拓扑被广泛应用到射频前端电子系统中，而基于纯粹或完全的单面单导体电路则非常少见。同时，这类单面单导体电路的分析与设计技术和方法都是非常成熟的，利用各种仿真工具都可以简单而轻松地完成，因此，这里不打算详细讨论这部分内容，感兴趣的读者可以参考本章末的相关文献。另外，由于射频微波传输线的种类繁多（参见前述各小节的介绍），因此，要用统一的原理或公式来包罗万象地阐述各种传输线的耦合机理是非常不现实的，也是不可能的。所以，我们只能根据不同的耦合结构采用不同的方法来阐述它们的工作机理。其中，本章主要讨论以双导体和三导体为代表的多导体耦合微带线、微带-CPW、微带-DGS以及微带-槽线等单面耦合和双面耦合。
2.3.1 微带对称双导体耦合理论 [1～7]
对于微带线耦合而言，对称双导体耦合结构支持奇偶两种模式。这些模式间的相互作用包括两传输线间的耦合，对称耦合结构的特性可以描述成这些模式的线性组合。图2.12（a）所示的耦合结构可以用图2.29所示的结构来描述。假定传输TEM模，则耦合传输线的电特性可以完全由线间的等效电容和在线上的传播速度来决定。如图2.29所示， C 12 是两个带状导体之间的耦合电容，而 C 11 和 C 22 则分别是每个带状导体和地之间的电容，若这些带状导体的尺寸和相对于接地导体的位置是相同的，则 C 11 = C 22 （均匀对称耦合线）。
图2.29 对称双线耦合结构及其等效电路
图2.30给出了奇偶模激励下的电力线分布。对于偶模，电场关于中心线偶对称，在两根带状导体之间没有电流流过。这时导出的等效电路如图2.30（a）所示，其中 C 12 等效于开路。这种情况下，每根导线和地之间产生的偶模电容 C e 为
假如这两根带状导体在尺寸和位置上是相同的，则偶模特征阻抗为
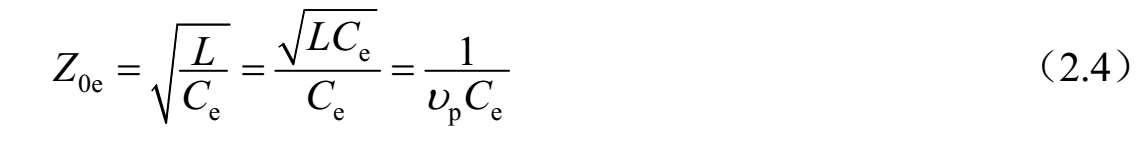
式中， υ p 是带状导体上传播的相速度。
对于奇模，电力线关于中心线奇对称，在两根带状导体之间存在零电压。这相当于在 C 12 的中间有一个接地面，其等效电路如图2.30（b）所示。这种情况下，每根导线和地之间产生的奇模电容 C o 为
图2.30 耦合传输线的奇偶模激励及其等效电路
假如这两根带状导体在尺寸和位置上也是相同的，则奇模特征阻抗为
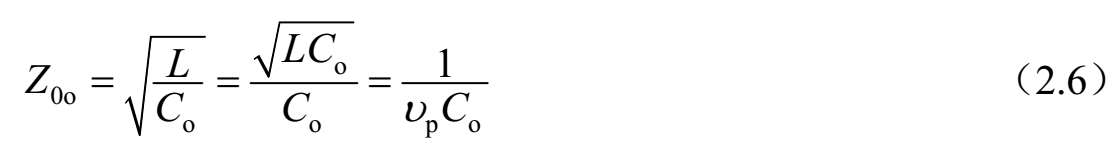
当耦合线工作在偶（奇）模时， Z 0e （ Z 0o ）是带状导体相对于地的特征阻抗。因此，耦合线的任何激励总可以看作是偶模和奇模对应振幅的叠加。假如耦合线传输的是纯TEM模，例如同轴线、平板线或带状线，则可以通过保角映射分析方法计算传输线单位长度的电容，然后决定偶模或奇模的特征阻抗。对于准TEM传输线，例如微带线，则可以用数值求解或用准静态近似方法得到这些结果。因此，一旦选定介质基片并获得相关参量（包括介电常数和基片厚度等），并通过上述方法计算得到一组特征阻抗 Z 0e 和 Z 0o 后，即可确定所需带状导体的宽度和耦合间距等几何尺寸。
2.3.2 微带不对称双导体耦合理论 [1～7]
尽管上述对称结构是很有用的一类耦合传输线，然而在一些实际情况下使用不对称结构设计电路可能更有用甚至是必需的。例如，在设计前向波耦合器时，使用不对称耦合结构获得的带宽将会比使用对称的要宽。另外，在某些情况下，其中一条耦合线的终端阻抗可能不同于另一条耦合线的阻抗，因此，选择不同特征阻抗的不对称耦合双线可能效果会更好。
本小节将会对微带不对称耦合传输线进行分析和设计。首先定义了不对称耦合线的标准模式参数，即给出了用于表征不对称耦合线的六个独立参数。推导了标准模式参数（即特征阻抗和相位速度）与传输线参数（即单位长度的电感和电容）之间的关系。由于对称线是不对称耦合线的一种特例，因此下面给出的各种表达式也可以用于对称耦合线，其结果与2.3.1小节给出的完全一致。
2.3.2.1 不对称耦合传输线参数
耦合双线能够支持两个基本独立的传播模式（即标准模式）。对于不对称耦合线来讲，这两种模式被称为 c 模和π模。严格来讲，由耦合双线组成的结构可以支持四个独立的传播模式，即两个后向模式和两个前向模式。但是，后向传输模式的特性（即相速和特征阻抗）与对应的前向传输模式相同。
1. c模
图2.31给出了两个均匀耦合的微带不对称传输线。之所以给出这种准TEM模式的假设，是因为与非TEM模式传输线相比，在这种情况下可以定义唯一的电压和电流。标记不对称耦合线上的c模电压和电流波，如图2.31所示。在耦合传输线1和2上的前向电压波分别记为
和
，对应的电流波分别记为
和
。类似地，
和
，
和
记为后向模式对应的参量。传输线1（紧临传输线2）的特征阻抗定义为
类似地，对于传输线2（紧临传输线1）的特征阻抗定义如下：
进一步，耦合双线上的电压比 R c 定义如下：
由上可知，耦合传输线的c模由如下四个参数表征，即模式传播常数 γ c 、耦合双线对应的特征阻抗 Z c1 和 Z c2 以及双线上的电压比 R c 。
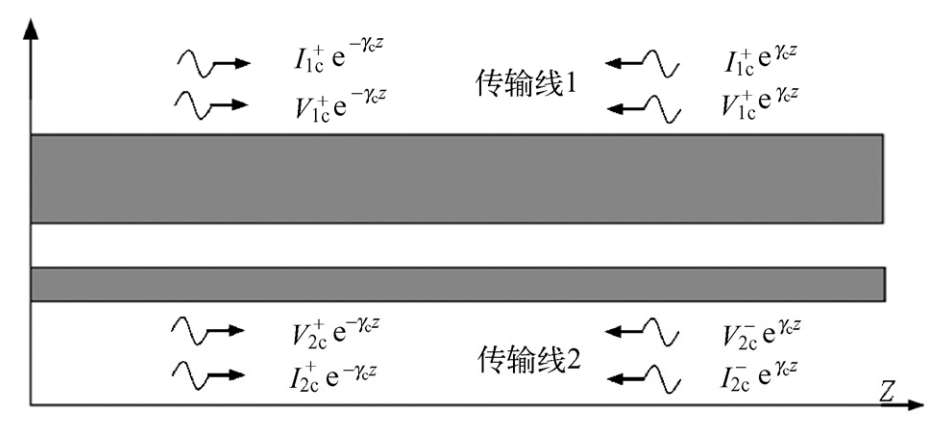
图2.31 均匀不对称耦合传输线上 c 模的电压和电流波
2. π 模
类似于c模，π模也可以用四个参数表征：模式传播常数 γ π ，耦合双线对应的特征阻抗 Z π 1 和 Z π 2 以及双线上的电压比 R π 。
分析表明，上述8个参数（c模和π模各4个）中，只有6个是独立的。其中，两个模式的电压和电流满足如下的关系：
和
因此，
和
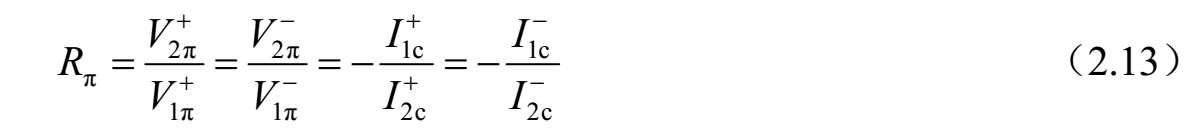
根据式（2.12）和式（2.13），特征阻抗 Z c1 、 Z c2 、 Z π 1 和 Z π 2 以及电压比 R c 和 R π 之间有如下关系：
因此，为了表征不对称耦合线，总共只需要6个参量（即 γ c 、 γ π 、 Z c1 或 Z c2 、 Z π 1 或 Z π 2 、 R c 和 R π ）就足够了。特别地，由于对称的耦合双线结构完全相同，因此可以进一步简化为由四个参数来表征，即任意一条耦合线的奇偶模特征阻抗 Z 0o 和 Z 0e 以及奇偶模相位常数 β o 和 β e 。而且，对于对称的耦合双线来讲，还有 R c =1和 R π =-1的结论。
3. 通过标准模式参数表征四端口网络的 Z 和 Y 参数
图2.32给出了不对称耦合双线的四端口网络。当其中的一个或更多的端口受到激励时，将会在两条耦合传输线上建立起电压和电流波。这两种波可以描述为前向和后向c模和π模的线性组合，如下所示：
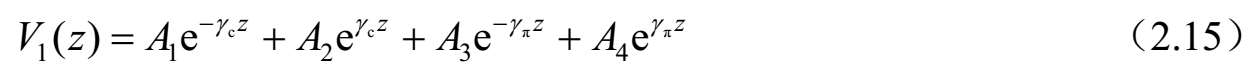
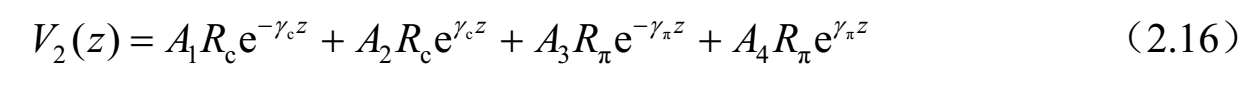
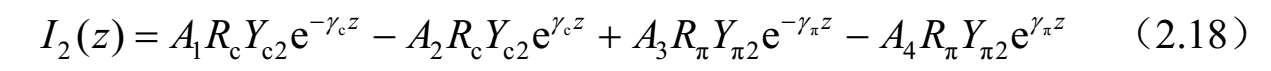
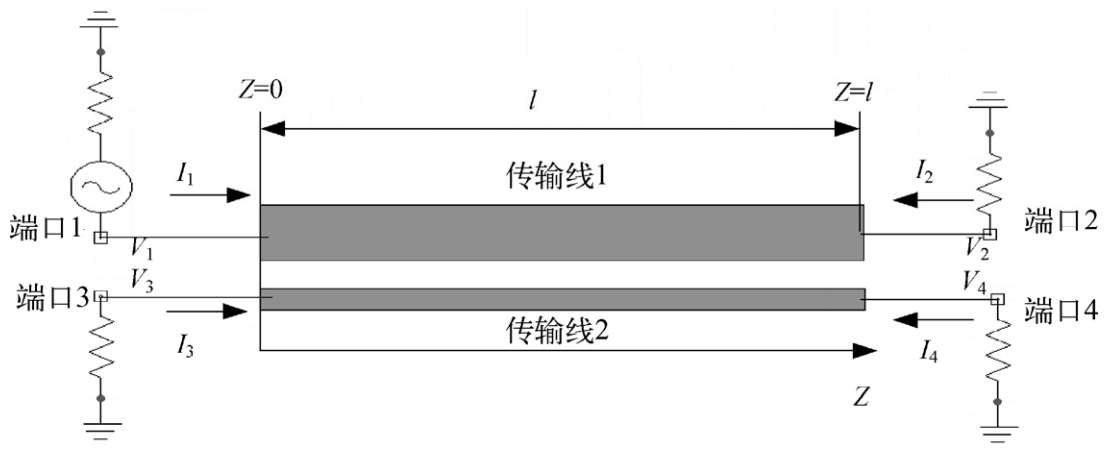
图2.32 均匀不对称耦合传输线构成的四端口网络
式中， Y c i =1/ Z ci ； Y π i =1/ Z πi （i=1，2）； A 1 、 A 2 、 A 3 和 A 4 是由源和终端确定的常数。将 z =0和 z =l代入式（2.15）～式（2.18），可以求得所有端口的电压和电流。例如，将 z = l 代入式（2.15），可得到端口2的电压（ V 2 ）。因此，各端口电压和电流如下：
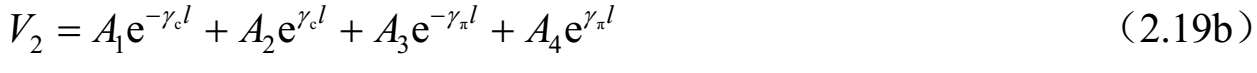
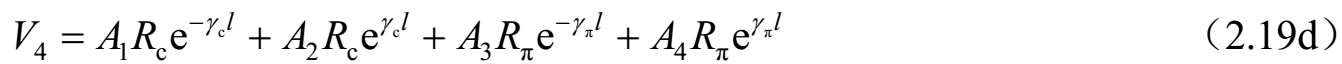
和
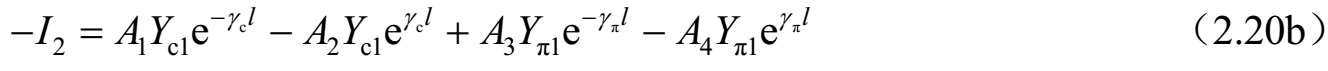
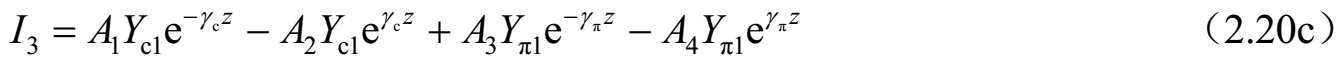
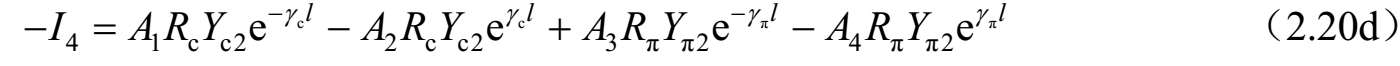
求解式（2.20a）～式（2.20d），可以获得由 I 1 、 I 2 、 I 3 和 I 4 表达的系数 A i （ i =1、2、3和4）。进一步，将这些结果代入式（2.19a）～式（2.19d），可以求得 Z 参数。因此，四端口网络的 Z 参数可以按照标准模式参数描述如下：
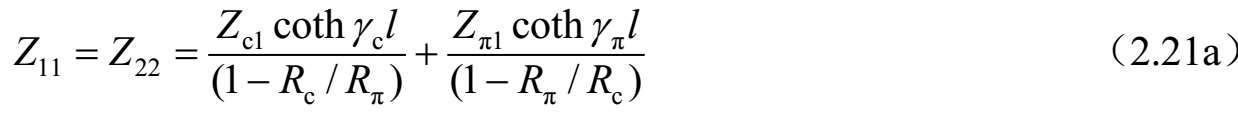
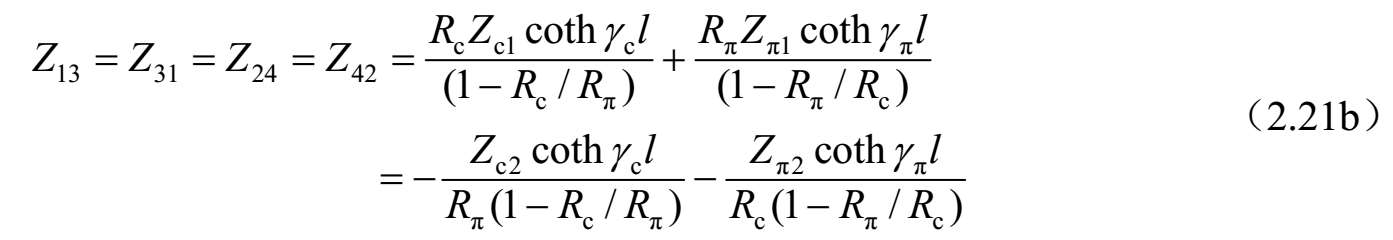
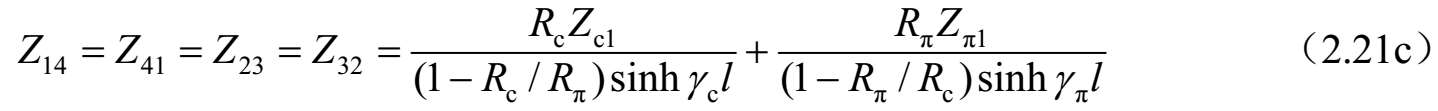
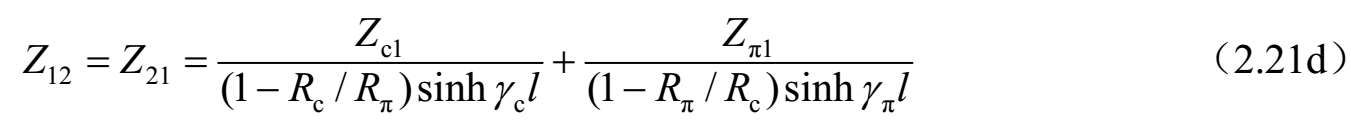
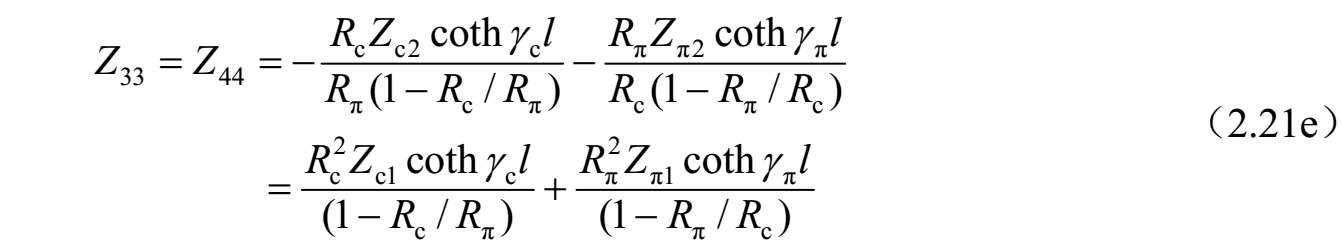
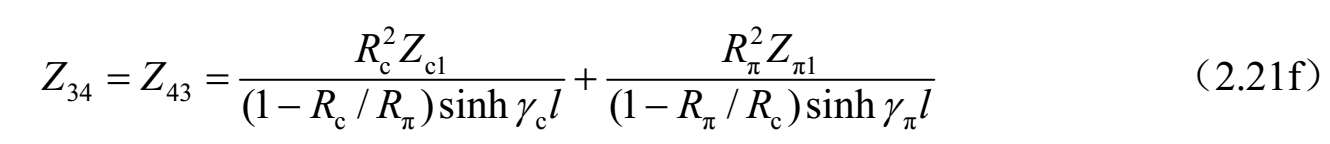
进一步，可以得到图2.32所示四端口网络的 Y 参数，如下所示：
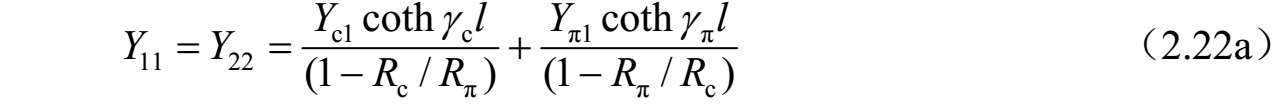
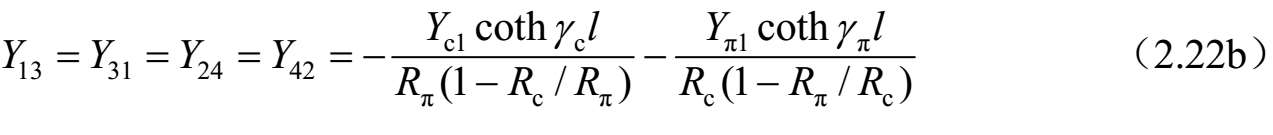
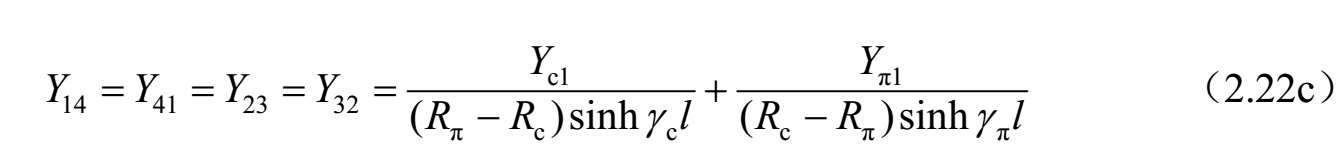
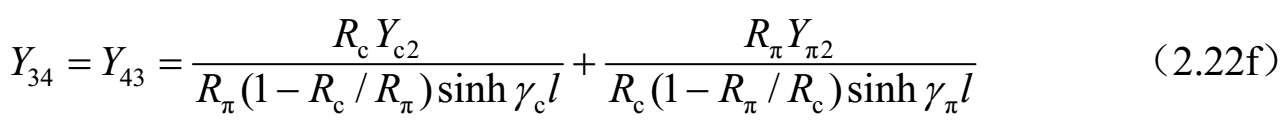
4. 交指耦合单元两端口网络的 Z 参数和 ABCD 参数
如果将图2.32中的端口2和3终端开路，则构成了图2.33所示的两端口网络，其相应的 Z 参数和 ABCD 参数分别如下所示：
和
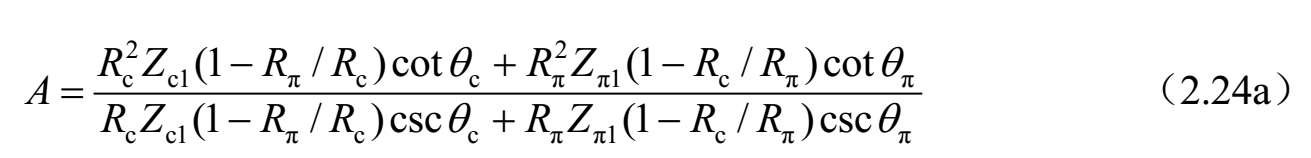
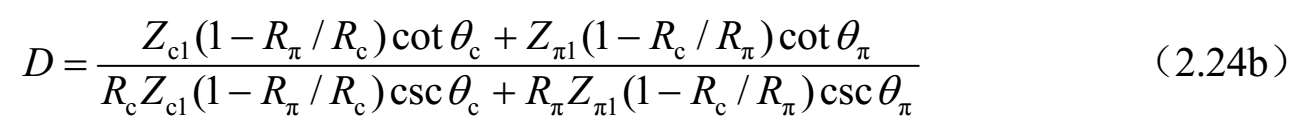
式中， θ c = β c l 和 θ π = β π l ，分别是不对称耦合双线c模和π模的电长度。该耦合结构在平面微波电路，例如平行耦合带通滤波器中有广泛应用。
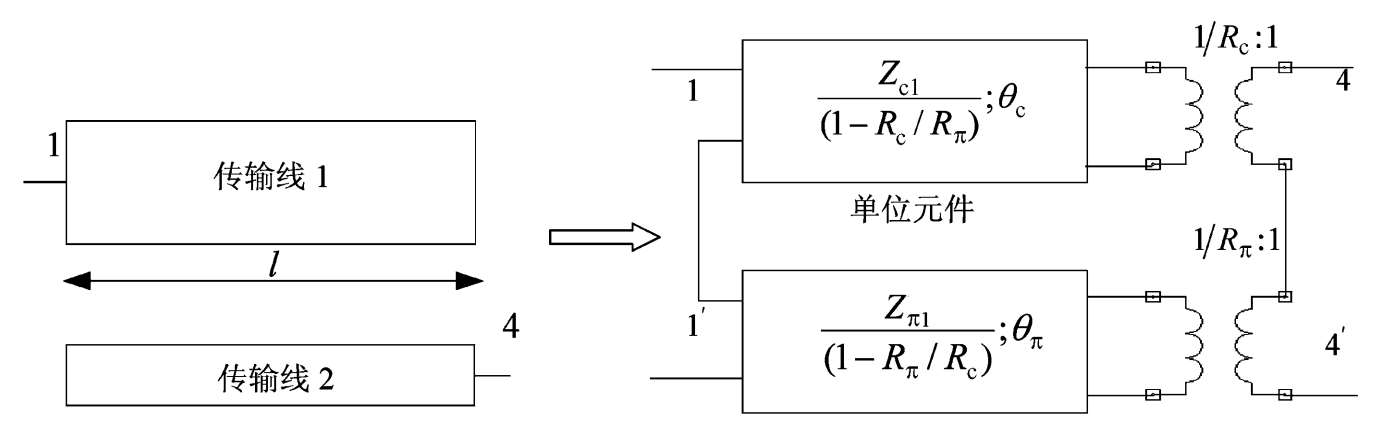
图2.33 均匀不对称耦合传输线的开路终端电路原型及其等效电路
2.3.2.2 耦合双线的等效电路
图2.34给出了无耗的均匀不对称耦合双线的等效电路。耦合传输线上的电压和电流由如下微分方程确定：
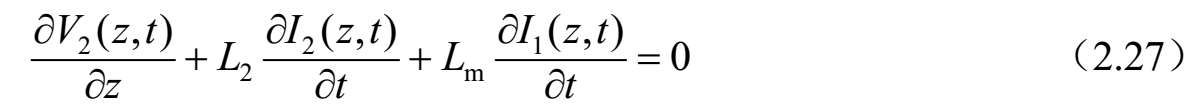
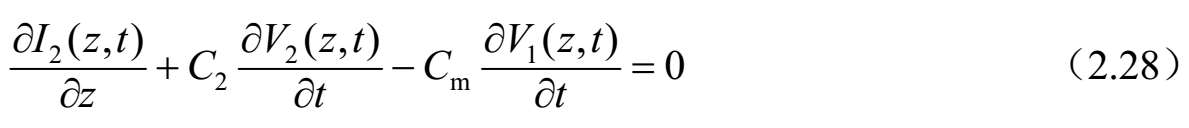
图2.34 微分长度为dz的不对称耦合双线的集总等效电路
式中， V i ( z , t )和 I i ( z , t )分别是传输线 i （ i =1，2）上的电压和电流，为沿传输线方向距离为 z 和时间 t 的函数； L 1 和C 1 分别是传输线1上单位长度的自感和自容； L 2 和 C 2 分别是传输线2上单位长度的自感和自容；L m 和C m 分别是线2和线1之间单位长度的互感和互容。特别地，自和互电感、电容参数是电感矩阵[ L ]和电容矩阵[ C ]的分量，其中：
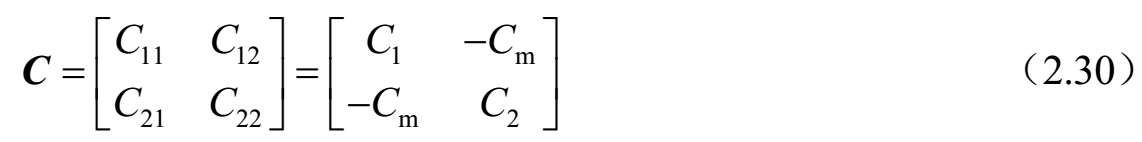
对于无耗的情况，电感矩阵可以由下式给出：
式中， C 0 是耦合传输线在自由空间的电容矩阵。由于式（2.29）是通用表达式，因此对于任意导体数目的耦合传输线均有效。
在频域，式（2.25）～式（2.28）可以简化为如下形式：
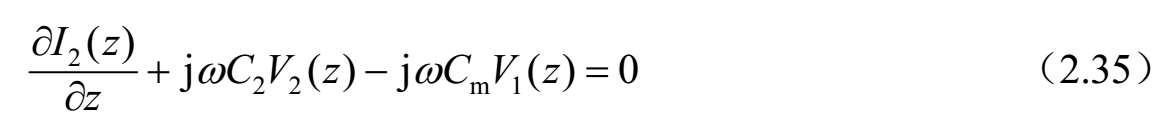
通过求解式（2.32）～式（2.35）的耦合传输线方程，可以得到先前定义的不对称耦合传输线的传播常数和其他参数。
推导得到的c模和π模的复传播常数如下：
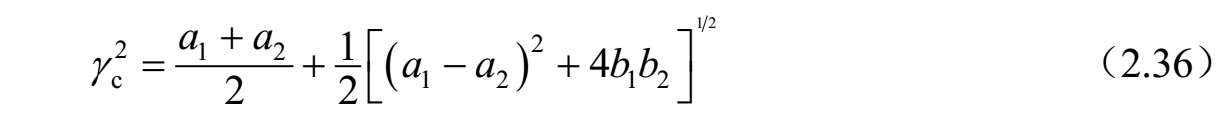
和
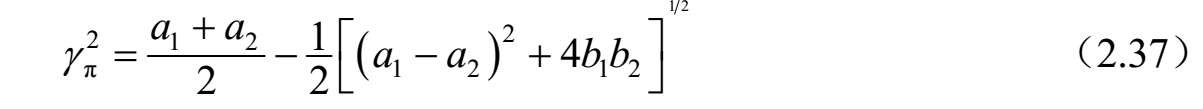
在上述方程中，
式中，
和
将式（2.38）中的 a 1 、 a 2 、 b 1 和 b 2 代入式（2.36）和式（2.37），可以求得c模和π模的相位速度：
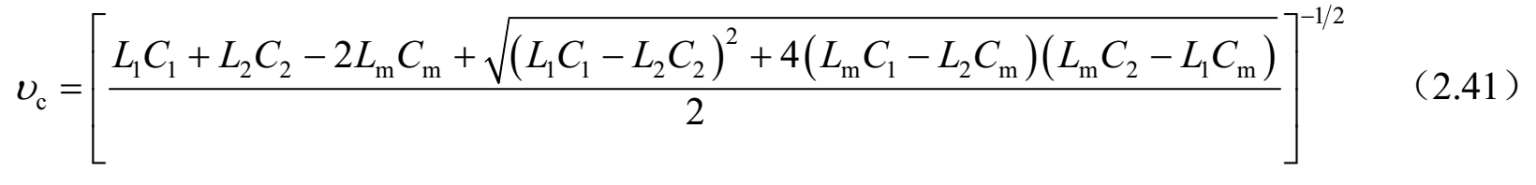
和
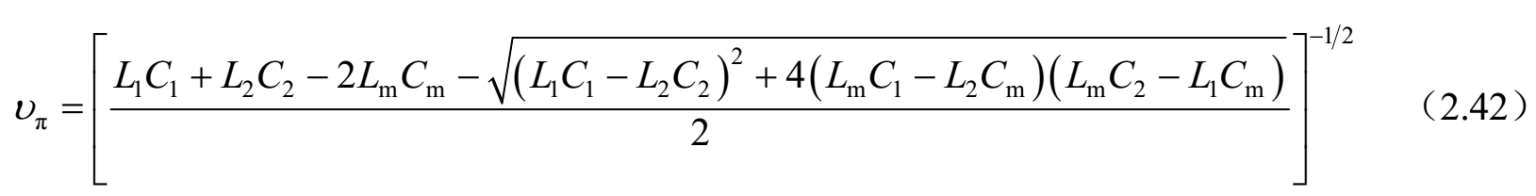
式中， υ c ,π = ωβ c , π 和 β c, π =−j γ c ,π 。而且，对于c模和π模的特征阻抗和特征导纳以及 R c 和 R π 参数由下式给出：
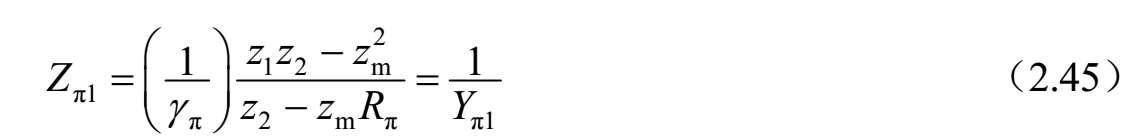
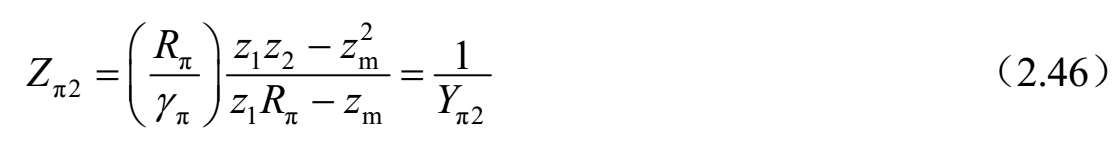
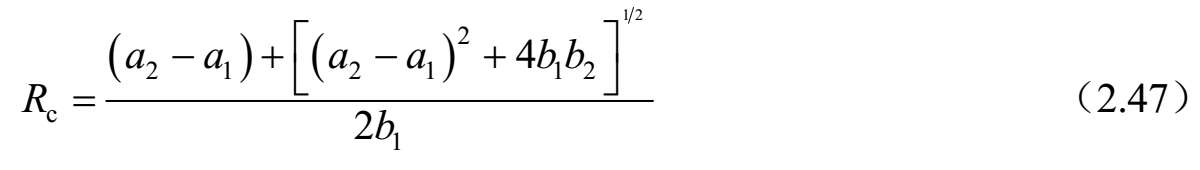
和
2.3.3 微带对称三线耦合理论 [1～6, 36～43]
在微带线等非均匀介质中的多导体耦合传输线结构可以应用于耦合器 [36] 以及其他电路单元。文献 [37] 分析了均匀介质（TEM模式）情况下的对称三线结构。图2.35给出了微带对称耦合三线系统的二维截面视图及其六端口电路原理图。为了便于分析和设计基于对称三线结构的耦合器、滤波器以及其他电路元件，这里将按照耦合传输线单位长度的自阻抗和导纳以及互阻抗和导纳参量求解对称耦合三线系统的模式特征参数以及六端口电路参数 [36, 38 ～ 42] 。
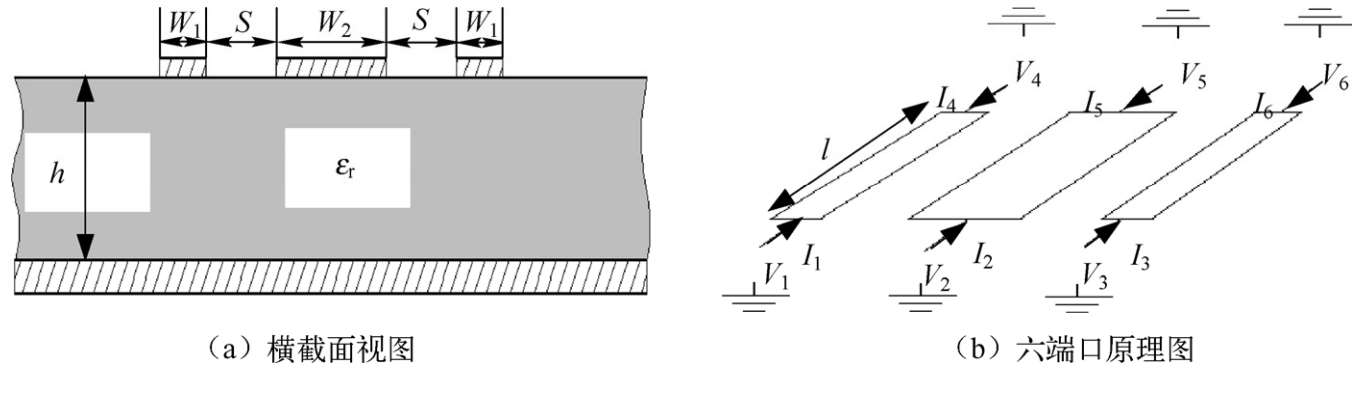
图2.35 对称三线耦合微带结构
式中， V 和 I 是三维列矢量； z 和 y 是3×3阻抗和导纳矩阵。对于对称情况下，有如下关系：
在三线上的电压和电流可以通过如下的传输线方程给出：
那么，对于这里考虑的非均匀介质耦合传输线情况下的电压和电流求解如下：
和
特征积矩阵 zy 和 yz 有如下形式：
和
其中，
求解方程| zy − γ 2 I |=0的本征值，可以得到按标准模式给出的对称三线耦合传输线的传播常数，即
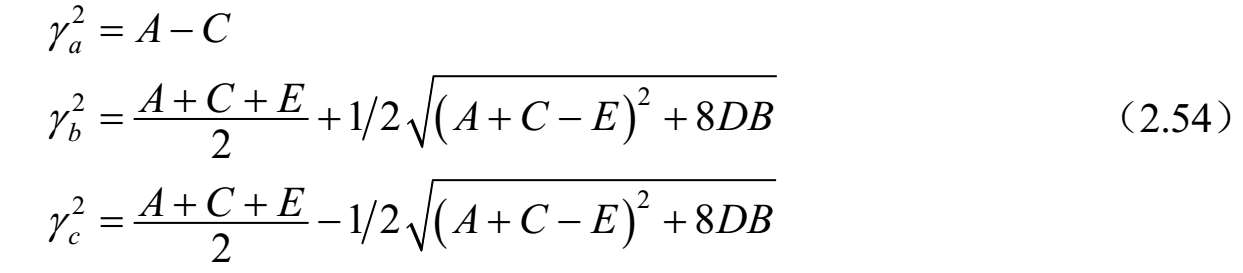
下面给出对应于电压和电流本征矢量矩阵相应的本征值：
和
其中，
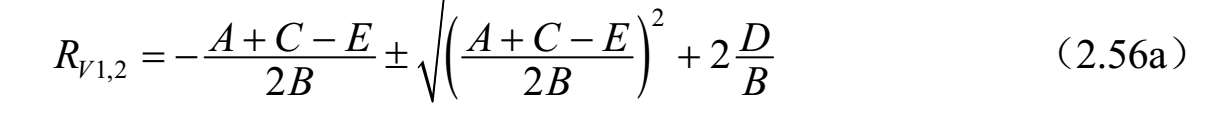
和
从式（2.54）可得
注意到，除非 D = B ，否则 R V 1,2 ≠ R I 1,2 ，即一般情况下耦合传输线上的标准传播模式电压比不等于其电流比，并且对于对称多导体系统的最初假设 R V 1,2 = R I 1,2 或[ M V ]=[ M I ]通常是不会得到标准独立模式的。在三线上的三个标准传播模式电压和电流本征矢量分别给出的两者之比可以用于求解三种标准模式的三线特征阻抗和导纳。
从式（2.49）可以得到如下的关系式：
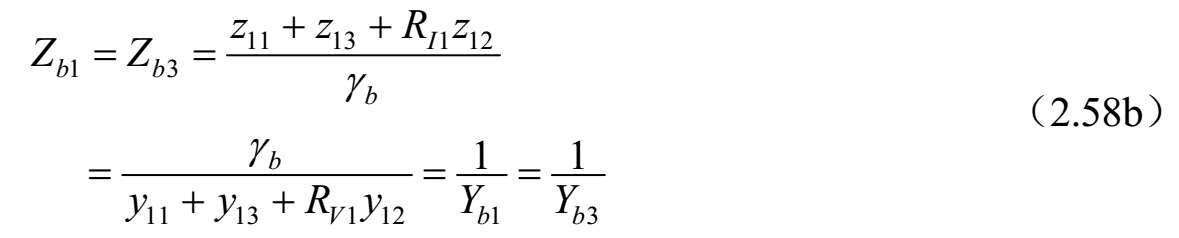
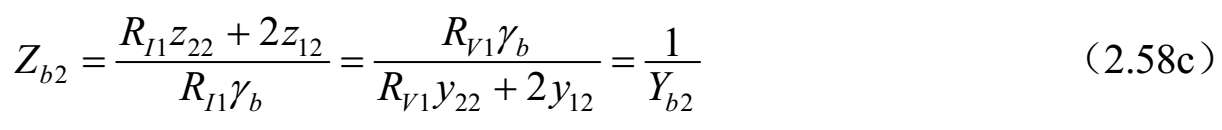
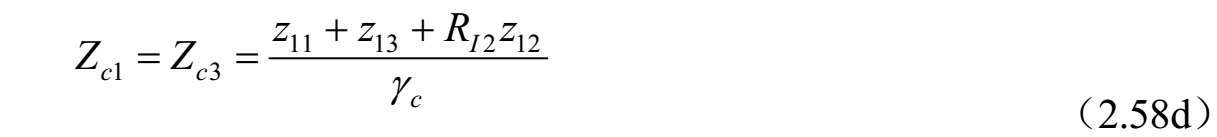
式中， Z jk 和 Y jk ( j = a , b , c 和 k =1, 2, 3)分别是传输线 k 的模式 j 的特征阻抗和导纳。从式（2.56）～式（2.57）可以看出，三种标准模式的传输线特征导纳通过如下等式相关联：
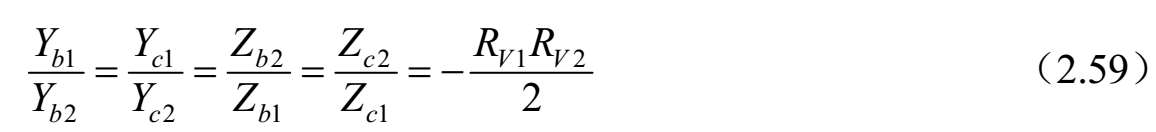
对称耦合传输线六端口（见图2.35）的导纳矩阵参数可以按照三线的标准模式特征导纳求得，电压和电流之比由式（2.55）～式（2.56）给出，而式（2.54）给出了标准模式的传播常数 γ a ,b,c 。这可以通过直接的方式实现，至于耦合线四端口的情况 [43] ，可以按照系统标准模式对六端口电压和电流方程进行改造。即 V=C V A 。其中， V 和 A 是六维列矢量，而[ C V ]是6×6矩阵，描述三种标准模式的端口电压 V 1 . .6 与前向波和反射波 A 1 . .6 的关系。端口电流也涉及这些幅度系数的关系，因为对线 k 上电流的每一种模式 j 通过 I k =Y jk V k 即 I=C I A 与电压相关联。消除幅度系数可以得到耦合线六端口的阻抗和导纳矩阵，其矩阵分量如下：
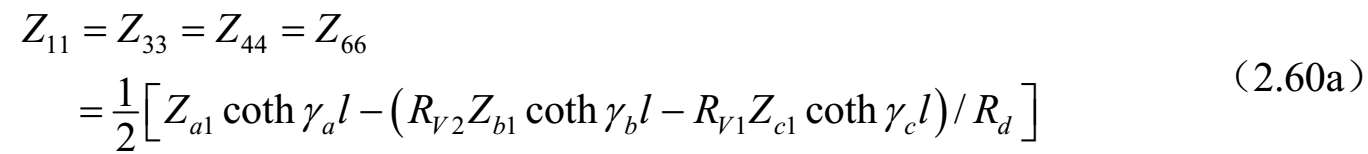
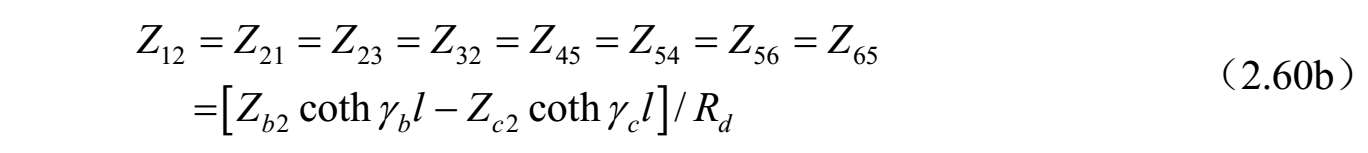
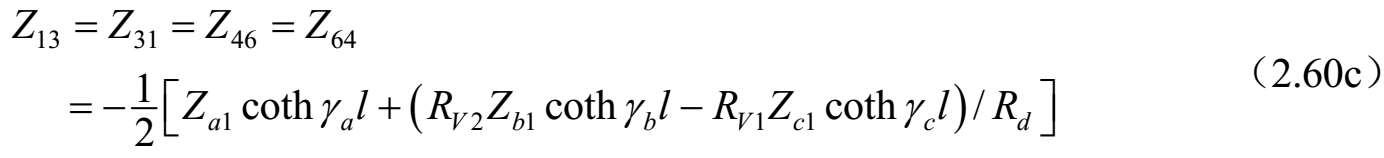
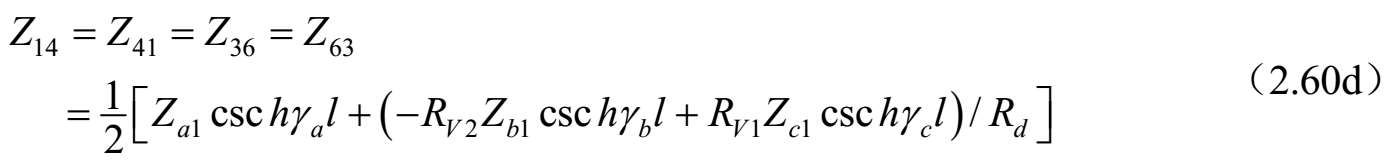
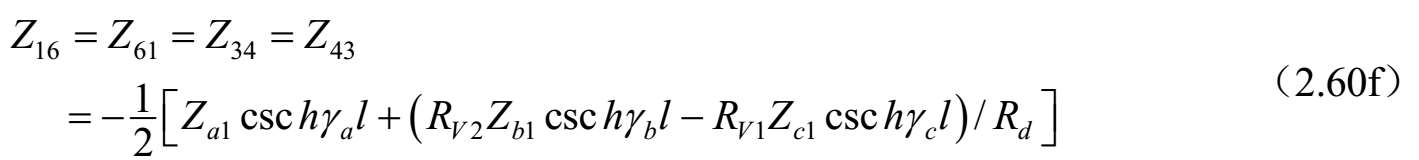
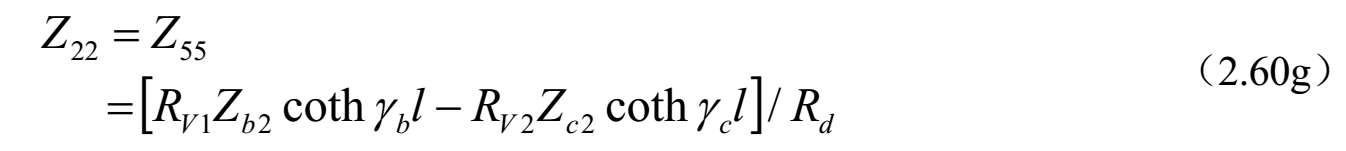
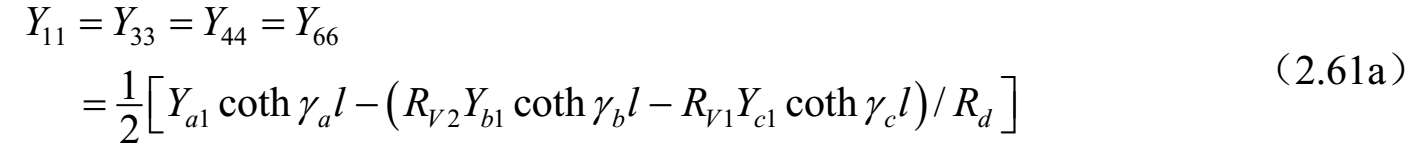
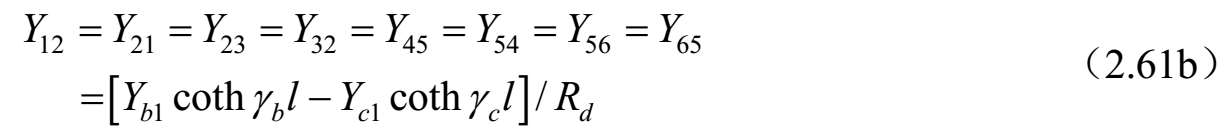
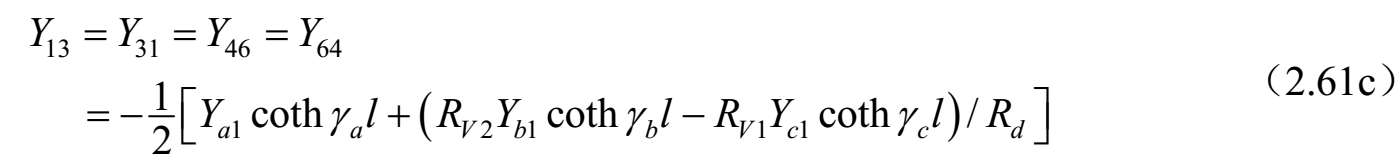
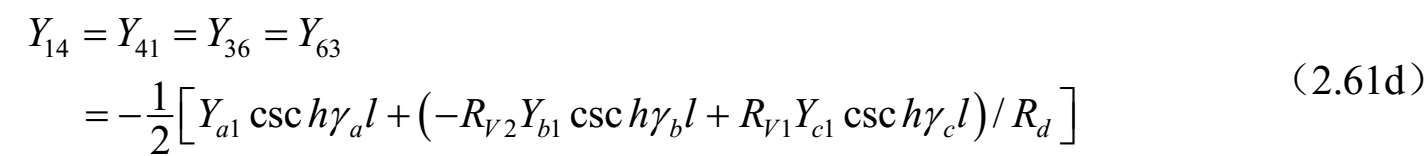
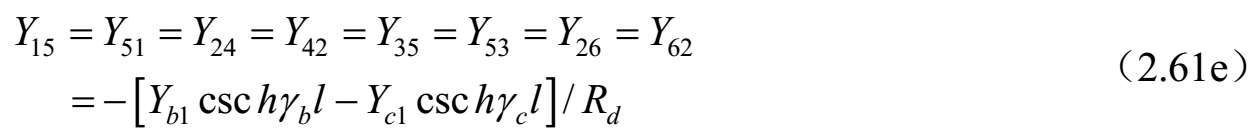
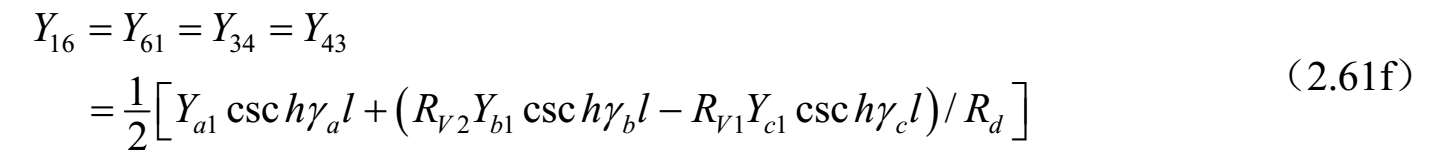
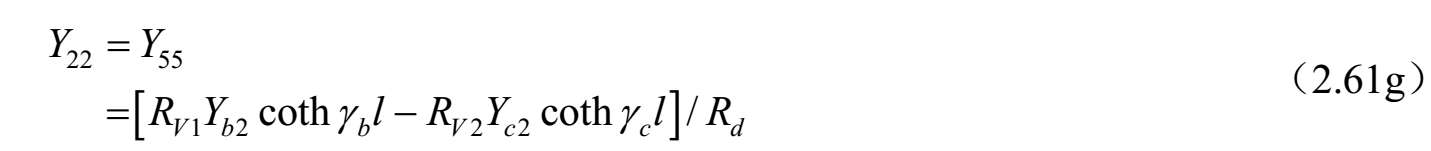
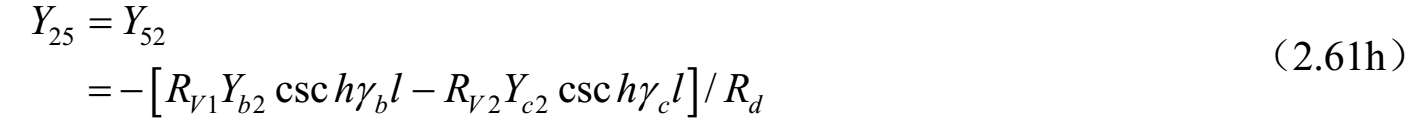
式中，
；
l
是传输线长度。
上述公式可以按照单位长度的等效自串联阻抗和互串联阻抗以及自并联导纳和互并联导纳来研究和评估任何对称三线系统的特性。对于无耗传输线的情况， γ a,b,c l =j β a,b,c l ，并且双曲函数可以被三角函数代替，即 γ a,b,c l =−jcot θ a,b,c 和csc hγ a,b,c l =−jcsc θ a,b,c 。其中， θ a,b,c = β a,b,c l 。 θ a,b,c 是三个标准模式传输线的电长度，在低频耦合微带线的准TEM情况下与频率线性相关。这种情况下，该结果可以按照结构的电容矩阵和同样结构但不带电介质的电容矩阵来表达。
当拿走三线中的一条导线，则上述分析结果可以简化到已知的耦合双线的情况
[43]
；同理，当三线参数按照特定方式相关联，则上述也可以变换到已知三线结果的情况
[36, 37]
。对于均匀介质的情况，本征值将会简化。并且可由
γ
a
=
γ
b
=
γ
c
=j
ω
推导出与Yamamoto等人[37]获得的结果相一致的结论，这对于研究耦合线六端口是很方便的一组本征矢量矩阵。对于无耗非均匀介质（例如准TEM模式）的情况，例如对低频的耦合微带线，假设
D=B
，则上述获得的结果可以简化到由Pavlidis和Hartnage
[36]
得到的结果。在先前推导的公式中，假定
M
V
=M
I
。对三线
D=B
的情况，由式（2.56）～式（2.57），有
假如利用由式（2.56a）给出 R V 1 的正确表达式，可以获得如文献 [36] 给出的由特征阻抗和六端口参数表示的结果。对这种情况，如果忽略非临近传输线之间的耦合（ y 13 = z 13 =0），则对于 D=B 的条件，需要如下关系：
当 z 11 = z 22 和 y 11 = y 22 ，这个显然满足。对于这种情况，则三个标准模式的模式电压比、传播常数和特征阻抗可由（2.54）、（2.56a）和（2.58）三式给出，如下所示：
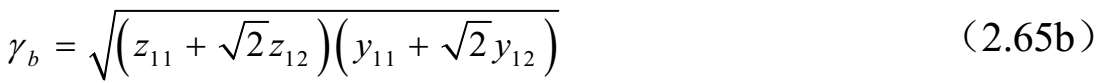
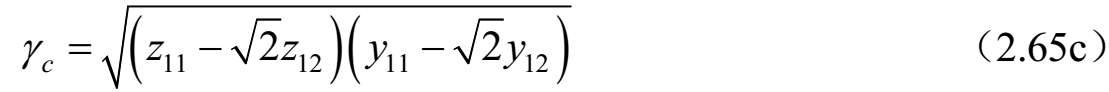
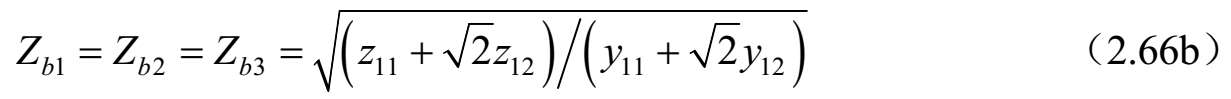
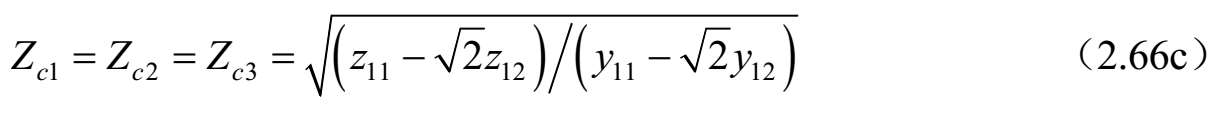
由于上述条件对由相同宽度且为松耦合的微带线组成的实验结构近似满足，因此文献[36]给出的实验结果与理论预测很吻合。但是，这里给出的一般情况下的微带对称三线结构的分析结果更适合于耦合器、滤波器和其他无源微波电路元件进行计算机辅助设计。
2.3.4 DGS通用电路模型 [44～51]
近年来，人们对平面传输线缺地结构（混合耦合结构）的频率响应表现出多个电磁带隙（EBG）或阻带特性 [44 ～ 50] 的兴趣日益增长。因此，新型紧凑的滤波器件可以基于周期或非周期的槽地结构（DGS）进行设计。但是，使用全波电磁仿真对槽地结构阵列进行直接优化设计是相当耗时的，特别是当电路中的槽地结构数量比较大时尤为如此。在此情况下，基于器件等效电路的优化是相当值得期待的。为此目的，获得槽地结构单元的既简单又精确的电路模型是相当关键的问题。文献[44]报道了利用集总元件电路模型对微带地平面一个相当特别的槽谐振器的最初两个谐振模式进行建模。特别是最近，报道了大量槽地平面的微带地缺陷结构的槽线电路模型 [45, 46] 。尽管这类使用槽线元件的电路模型能够描述周期频率响应，但是对于计算槽线有效介电常数和特征阻抗需要精确模型，因为这两个参数是高度频率相关的。结果是，这类电路模型应该更加适合于简单横向槽，但这些槽并不包括许多不规则结构的不连续性，如文献[46]所述。
2005年，J.-S. Hong博士提出了一种适用于平面传输线缺陷地结构（DGS）的通用电路模型 [51] 。图2.36给出了一些槽地结构的实例。图2.36（a）是常规的微带双哑铃形DGS，图（b）和（d）分别代表了CPW和微带L形DGS，而图2.36（c）和（e）结构则分别代表了CPW和微带上的金属加载哑铃形DGS。这些DGS单元拥有一些有趣的特性用于开发基于DGS的滤波器件。例如，图2.36（c）和（e）所示的哑铃形DGS内浮动金属不仅能够用于控制最初两个谐振模式的间隔，而且也能很方便地进行用于电调谐的DC偏置。本小节主要集中在上述器件的等效电路建模上。
图2.36 各种DGS结构
2.3.4.1 电路理论
包括图2.36所示电路在内的许多DGS表现出多阻带频率特性，图2.37给出了这类DGS直到第二阻带的典型频率响应，其中， f 0 1 和 f 0 2 分别是第一和第二谐振频率，f T 是过渡频率。对许多DGS器件设计而言，最感兴趣的是频率范围达到第二阻带。因此，这里提出的电路模型（见图2.38）仅仅考虑第一和第二谐振模式。这样，在微带或CPW上的DGS单元可以通过两个LC谐振器（即 L 1 、 C 1 ， L 2 、 C 2 ）与由 C p 、 L s 1 、 L s 2 组成的T形网络连接来建模。该T形网络本质上代表了两个谐振器之间的相互作用。低于过渡频率 f T 则第一谐振器主导频率特性，而高于过渡频率 f T 则第二谐振器主导频率特性。
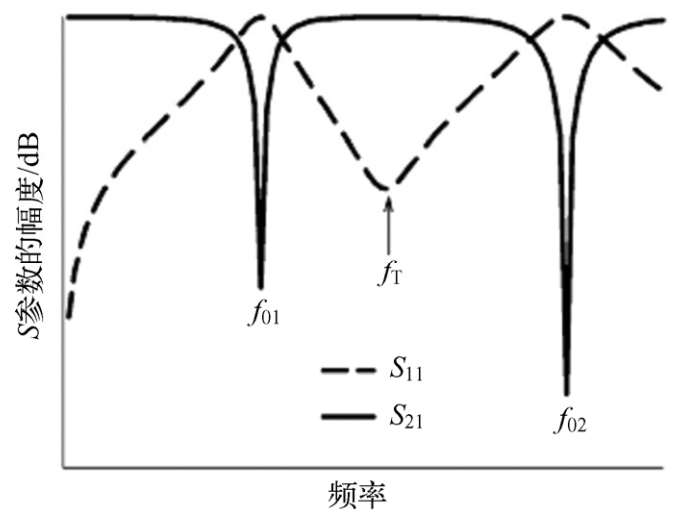
图2.37 表现出多阻带特性的DGS典型频率响应
图2.38 DGS通用电路模型
图2.38中， Z 0 是传输线特征阻抗。为了提取所有其他电路参数，下列数据是必须的，并容易从电磁仿真中获得： f 0 1 、 f 0 2 、 f T 、Δ f 3 dB _1 （@ f 0 1 处的3dB带宽）和Δ f 3 dB _2 （@ f 0 2 处的3dB带宽）， X 11 、 X 22 和 X 21 是三个在 f T 的 Z 参数的虚部。由电路理论可知，
式中， i =1, 2。其中式（2.67）可以从传输线参数（即当 S 21 是按照谐振器导纳表示时，单个两端口谐振器网络的 S 21 ）中推导出来，而式（2.68）可以通过匹配两端口T形网络的 Z 参数来获得。
2.3.4.2 建模与讨论
应用2.3.4.1节提出的电路模型建模各种DGS，得到的结果与电磁仿真和/或测量结果非常一致。本节给出一些实例。
实例1
图2.39（a）所示CPW DGS制作在相对介电常数为10.8，基片厚度为1.27mm的介质上。图中单位均为毫米（mm）。为了建模，两个参考平面按照图中所示箭头方向从端口移动，CPW线在参考平面的特征阻抗为50Ω。从电磁仿真中提取电路参数： C 1 =0.8966pF, L 1 =1.226nH, C 2 =1.632pF, L 2 =0.2212nH, C p =0.033pF, L s1 =0.995nH, L s2 =-0.919nH。注意：对电路模型而言， L s1 和 L s2 为负值是完全许可的。这种情况类似于带负值元件的集总元件倒置器，其中的负值元件在电路中被临近电抗元件所吸收。
图2.39（b）和（c）分别给出了理论（电路模型）与全波电磁仿真的 S 参数幅度和相位响应结果。由此可知，两种仿真结果非常一致。图2.40（a）、（b）和（c）则分别给出了本例CPW-DGS复合结构在通带内的典型频点（ f p =5.55GHz）以及在两个主要谐振频点 f s 1 =4.45GHz和 f s 2 =8.3GHz的电流分布。
图2.39 CPW DGS模型的布线以及理论（电路模型）与全波电磁仿真（Sonnet EM）
结果的幅度响应和相位响应
实例2
第二个建模实例是微带L形DGS，如图2.41（a），所有单位均为毫米（mm）。使用相对介电常数为10.8，基片厚度为1.27mm的介质。微带线特征阻抗在参考平面为50Ω。此例中，从电磁仿真提取得来的参数： C 1 =1.349pF, L 1 =0.4184nH, C 2 =1.02pF, L 2 =0.082nH, C p =0.028pF, L s 1=0.749nH, L s 2=0.5745nH。该DGS有两个宽间隔的谐振模式，而且理论（电路模型）与全波电磁仿真结果非常一致，如图2.41（b）所示。同时，相位响应结果也很一致。
图2.40 DGS结构在各种频率条件下的电流分布
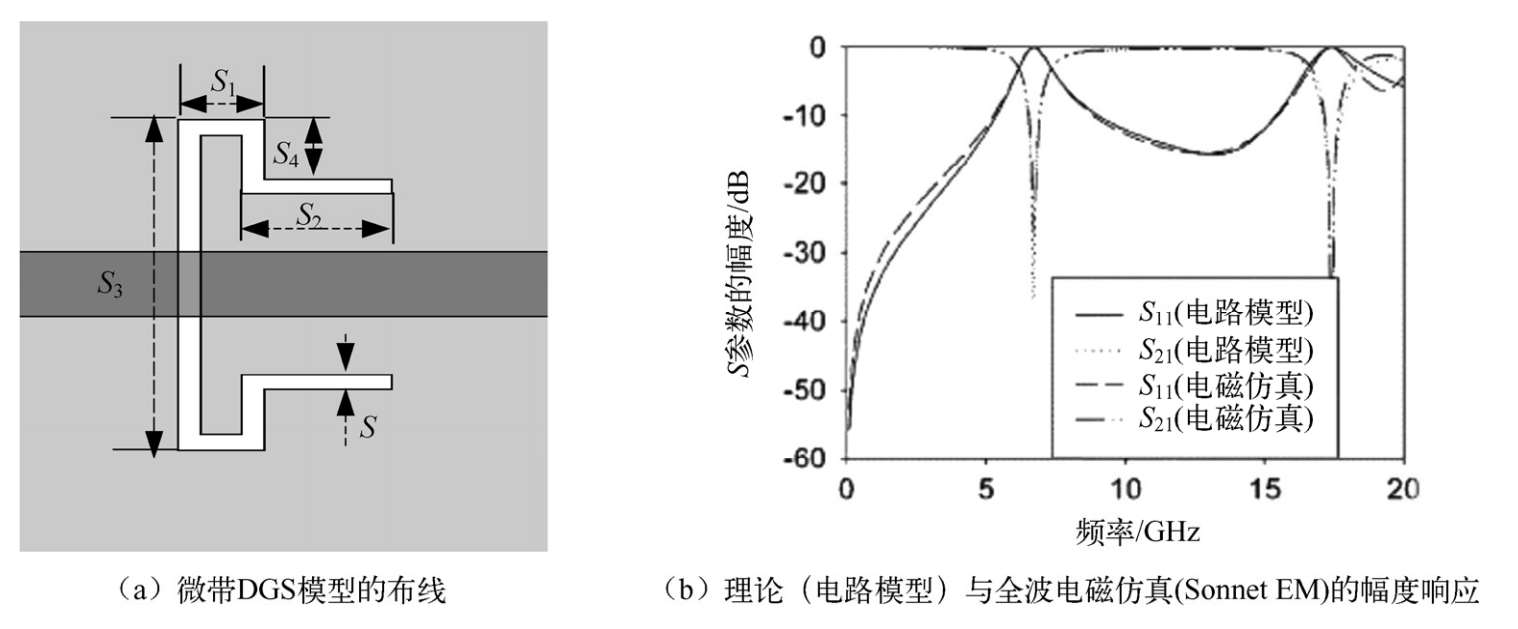
图2.41 微带L形DGS
图2.42（a）和（b）分别给出了本例微带-DGS复合结构在两个主要谐振模式 f 0 1 =6.6GHz和 f 0 2 =15.9GHz的电流分布。
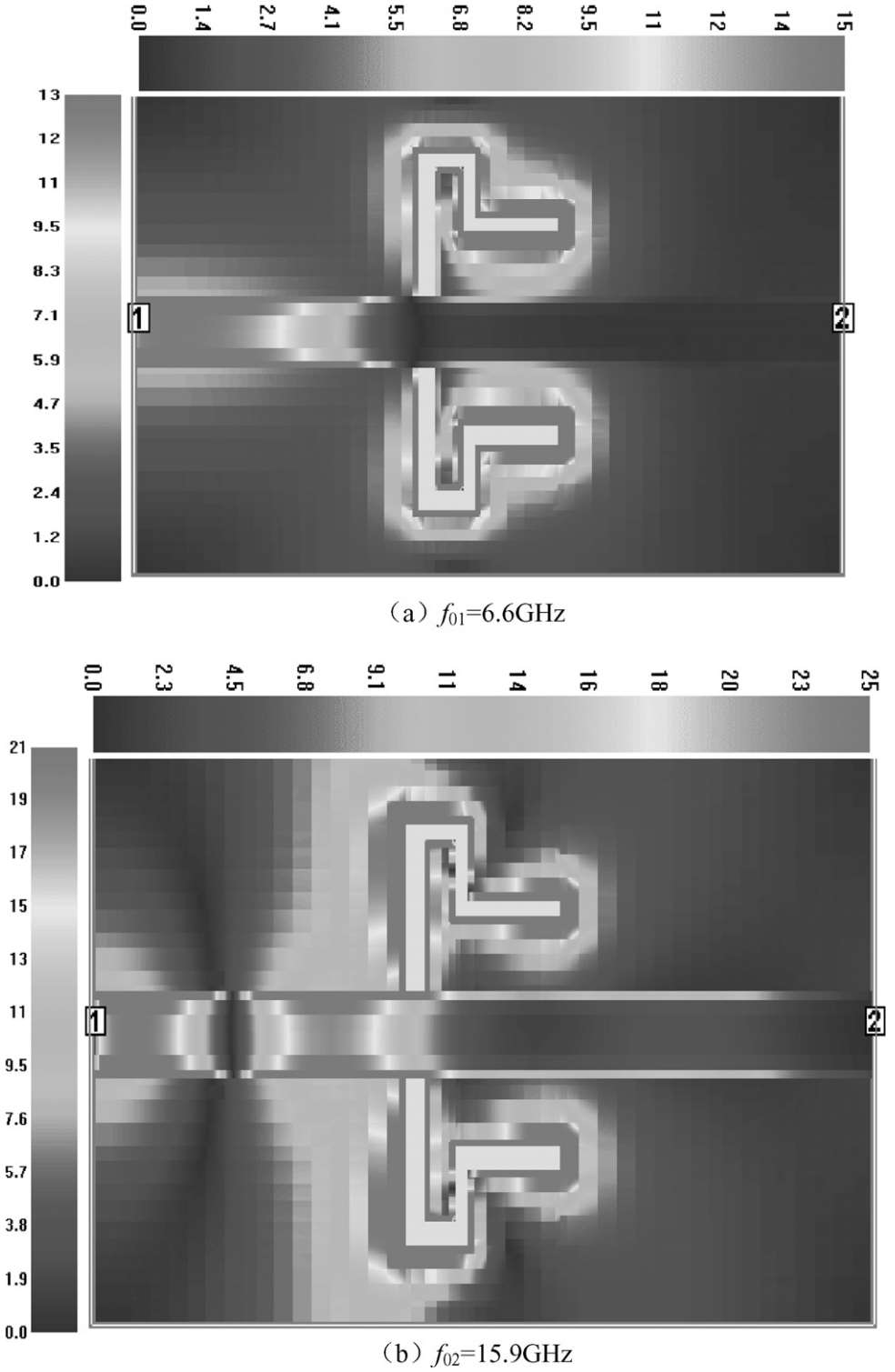
图2.42 两个主要谐振模式的二维电流分布（单位：A/m）
实例3
该例阐述了本小节提出的周期性CPW DGS电路模型的应用，如图2.43（a）所示。使用相对介电常数为10.8，基片厚度为1.27mm的介质。这里使用的结构单元是图2.36（b）所示DGS单元。电路尺寸如图所示，从电磁仿真提取得到的电路参数： C 1 =2.059pF, L 1 =0.8746nH, C 2 =1.457pF, L 2 =0.2303nH, C p =0.0385pF, L s 1 =1.009nH, L s 2 =1.093nH。谐振单元的周期长度为7.75mm。该三单元DGS器件的等效电路可以简单地通过交替地级联如图2.38所示单元电路模型和7.75mm长传输线得到。图2.43（b）给出了电路模型、全波电磁仿真和测量得到的S参数。结果表明，模型与仿真和测量结果非常一致。
图2.44（a）、（b）和（c）分别给出了本例三单元CPW DGS复合结构级联滤波器在低通带典型频点（ f p 1 =2.0GHz）、阻带典型频点（ f s =3.75GHz）和高通带典型频点（ f p 2 =6.0GHz）的电流分布。
图2.43 周期性CPW DGS
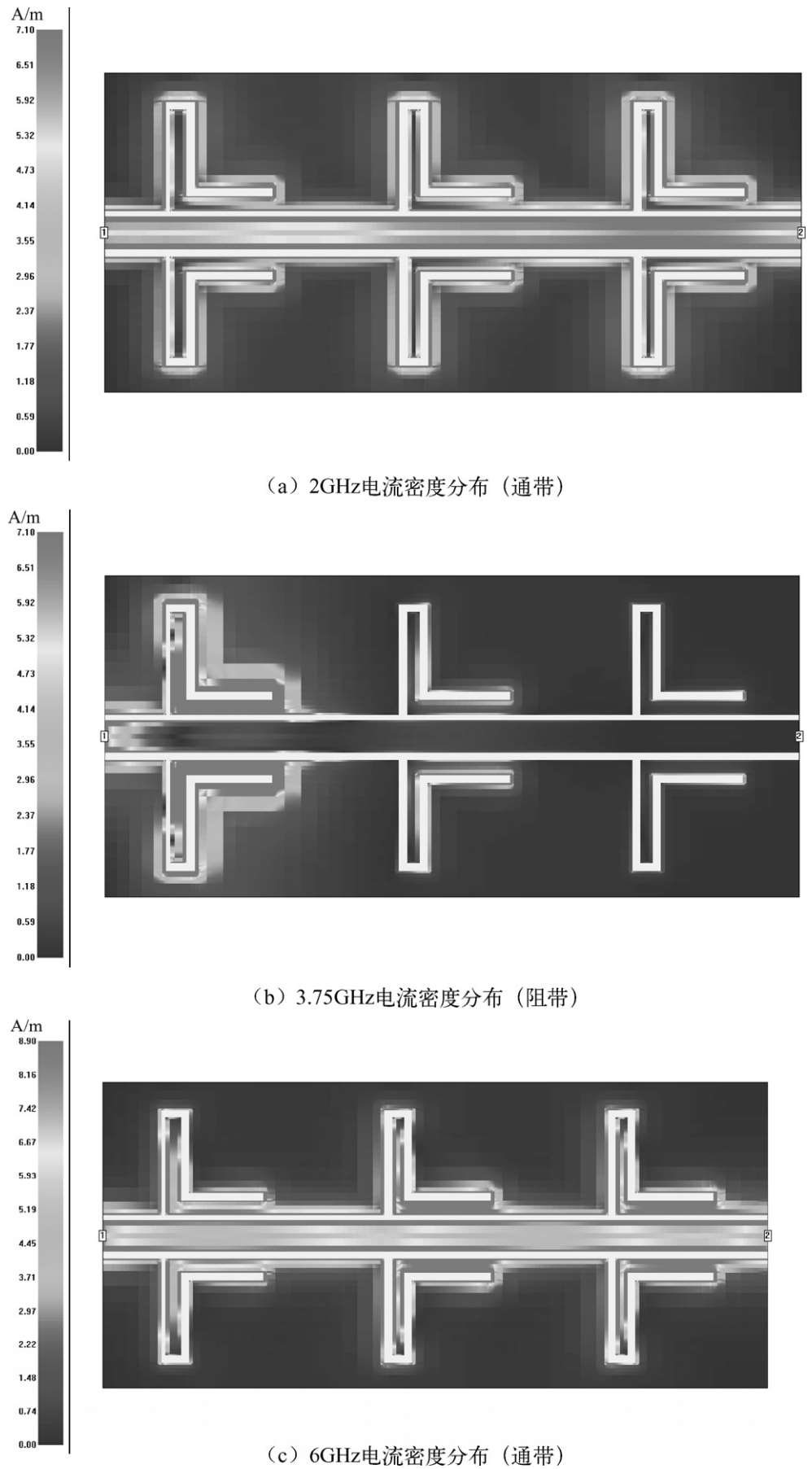
图2.44 三单元DGS加载传输线
2.3.4.3 结论
本小节阐述了各种DGS的一种通用电路模型，同时给出了电路参数提取的简化公式。阐述了提出的电路模型应用，结果表明：全波电磁仿真、测量与电路模型有很好的一致性。这些等效模型及其集总元件的提取公式可以应用到后续章节有关双面PCB电路的分析与设计中。
2.3.5 DMS的建模与分析 [52～63]
近年来，人们对结合了扰动或修正的地平面结构，例如缺地结构（DGS）、光子带隙结构（PBG）和电磁带隙结构（EBG）等平面微带结构的研究兴趣日益增长。DGS通过在地平面刻蚀特定的图形如哑铃形、螺旋形等来实现，这种结构由于改变了传输线的等效电感和电容从而提供了阻带抑制特性。DGS和PBG两者用于改进各种微波电路，如功率放大器、滤波器和天线等的性能是非常有效的 [52 ～ 56] 。
受到DGS概念的启发，研究人员又提出了平面传输线的修正形式—缺微结构（DMS）。通常，这种结构是通过在微带线的信号层刻蚀T形槽来实现的。微带线上的槽会扰动在带条上的电流分布，并提供阻带频率响应特性。与DGS一样，DMS也用于改进微波电路的性能，如谐波终端网络功率放大器 [57] 、滤波器 [58, 59] 和天线 [60] 等。同时，基于周期或非周期DMS也可以设计新型紧凑的滤波器件 [61] 。
然而，使用全波EM仿真直接对DMS阵列进行优化设计将会是一个真正耗时的过程。因此，基于器件等效电路的优化是非常理想的。为了解决这个问题，获得DMS单位元件的简单和精确模型是问题的关键。文献[62]已经报道了采用集总元件模型建模DMS传输线。但是，该报道的模型只提供了单阻带特性DMS的等效电路。同时，对等效电路模型的研究是非常有限的。
2011年，G. Chaudhary等人 [63] 提出了一种G形缺微结构，并分析了它的频率响应特性。同时也提出了一种新的方法用于提取修正平面DMS传输线的电路模型，该结构的频率响应表现出双阻带特性。提出的等效电路由集总元件组成，这容易通过全波电磁（EM）仿真提取。在整个的宽带带宽内，这是提出的DMS的简单和精确的电路建模。提出的建模方法通过仿真和测量结果两者很好的一致得到证实。
2.3.5.1 G形DMS的电气特性
图2.45（a）是常规T形DMS的原理视图。DMS的配置提供缝隙高度 L 2 和垂直于带条方向宽度为 W 2 以及槽长 L 1 和沿带条方向宽度 W 1 来描述。通常，槽隙提供电容效应而窄微带线表现出电感效应。因此，给定所需工作频率和对诸如带阻特性等频率响应的影响，则增加慢因子等。而且，一种新型G形DMS如图2.45（b），图中给出了物理参数。为了比较常规和提出的DMS性能，使用了介电常数2.2、高度为31mil的罗杰斯公司RT/Duroid 5880介质基片。DMS参数分别为 W = W s =2.7, L = L s =30, L 1 =17.6, W 1 =0.4, W 2 = W c =0.3, L 2 =1, L a =8.6, L b =9, L c =0.8, W a =0.4和 W b =0.3mm。
仿真使用Ansoft公司的 HFSS V11.0，频率响应特性如图2.46所示。由图2.46可知，常规T形DMS结构只能获得单一谐振频率的响应，而这里讨论的新型G形DMS结构则表现出双频谐振特性。
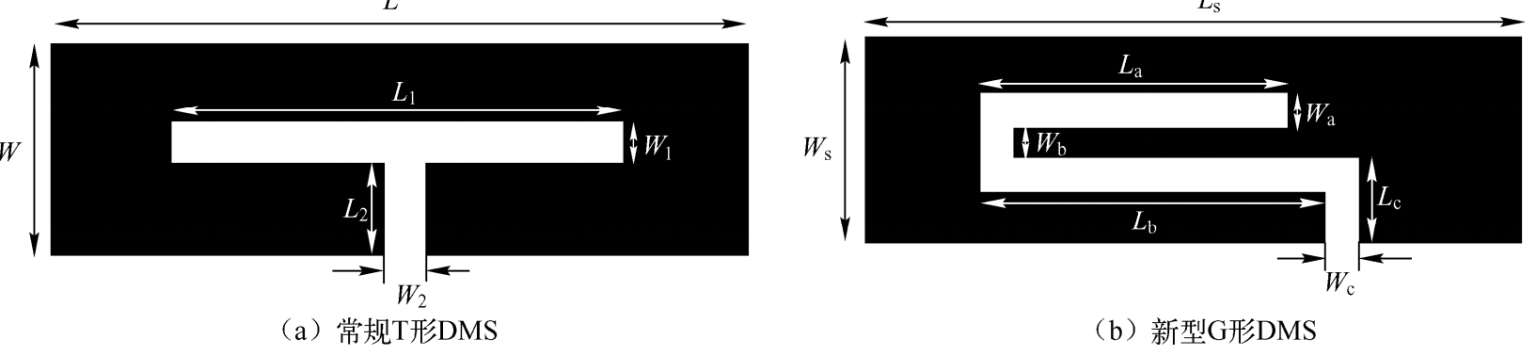
图2.45 缺微结构示意图
图2.46 仿真的常规T形和提出的G形几何结构的频率响应特性
为了深入分析新型G形DMS结构的几何参数对谐振器性能的影响，在保持其他参数不变的条件下，我们来较为详细地分析物理尺寸 L a 和 L b 变化产生的结果。图2.47（a）所示为仿真得到的 S 参数随不同的 L b 长度变化的频率响应，而图2.47（b）所示则为仿真得到的 S 参数随不同的 L a 长度变化的频率响应。
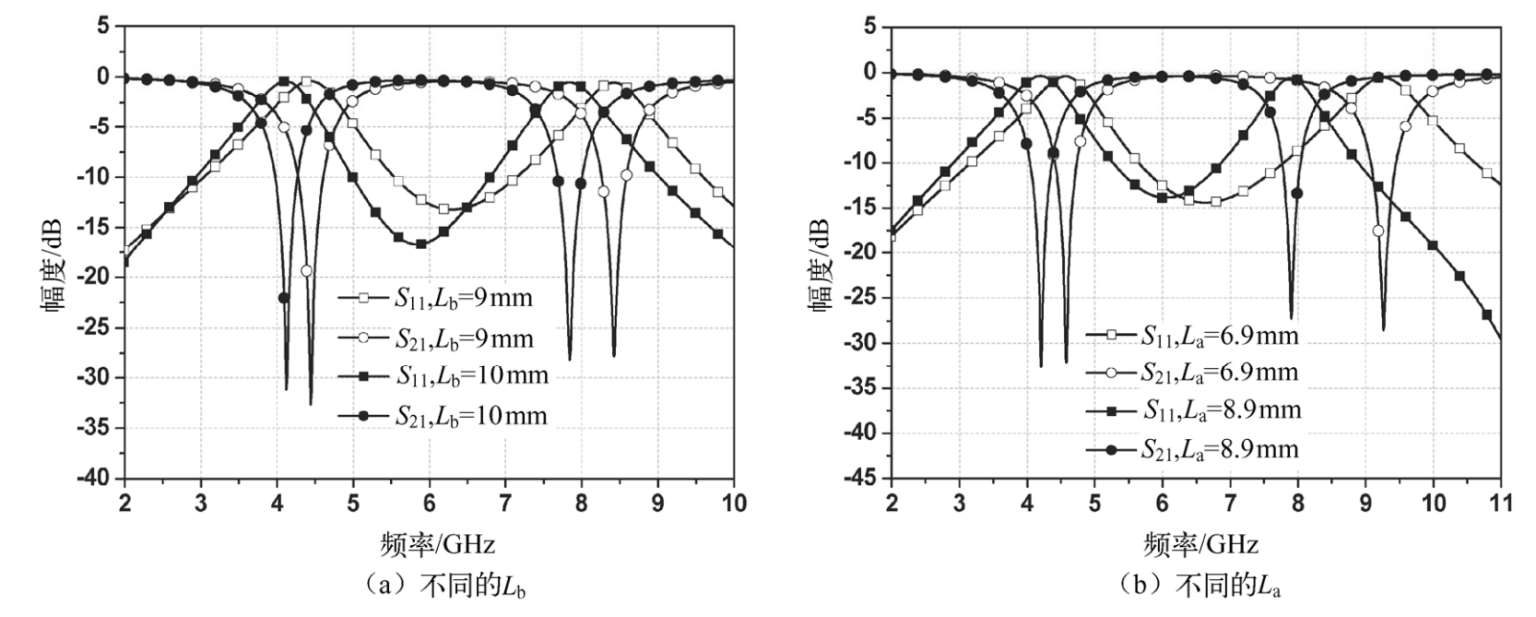
图2.47 G形DMS在不同的物理尺寸变化下产生的频率响应
表2.1和表2.2分别总结了G形DMS几何参数对其谐振性能的影响，结论如下：（1）随着长度 L b 的增加，第一谐振频率慢慢下移，而第二谐振频率则较快下移至频率低端。（2）同理，随着 L a 尺寸的增加，第一和第二谐振频率也都下移至低频端。
表2.1 不同长度 L b产生频率响应结果
表2.2 不同长度 L a产生频率响应结果
2.3.5.2 电路模型
图2.46所示为G形DMS的典型频率响应，其中， f 0 1 和 f 0 2 分别是第一和第二谐振频率，而 f T 则是转换频率。考虑到这里提出来的新颖G形DMS的双阻带特性，其典型电路可以用如图2.48所示的模型来描述。因此，G形DMS几何单元可以通过两个LC谐振器和T形网络互连来建模。也就是说，两个并联谐振单元L ps 1 和C ps 2 以及L ps 1 和C ps 2 ，然后再与由C p 、L s1 和L s2 组成的T形网络互连组成。T形网络本质上可以描述为两个LC并联谐振器之间的相互作用。当工作频率低于过渡频率 f T 时，则第一谐振器主导DMS的频率特征，而当工作频率高于过渡频率 f T 时，则第二谐振器主导DMS的频率特征。
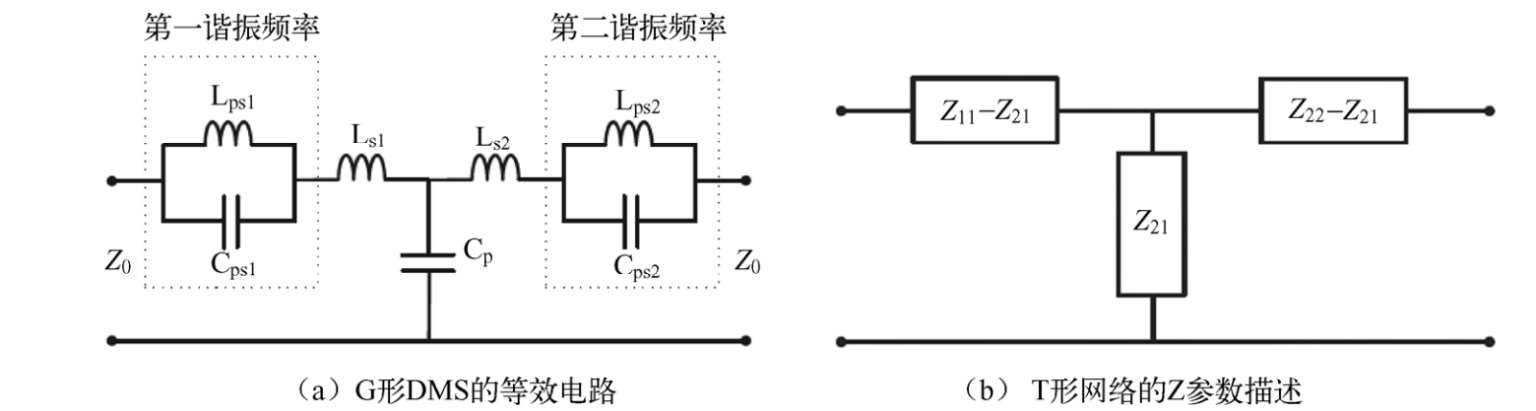
图2.48
细心的读者可能会发现，本小节讨论的G形DMS等效电路与2.3.4节讨论的DGS的等效电路完全相同，因此，提取图2.48集总元件参数的方程也应该是完全相同的，即完全可以由式（2.67）～式（2.70）给出。
2.3.5.3 建模结果与讨论
为了验证这里提出来的电路模型，G. Chaudhary等人构建了一个新颖的DMS，其物理参数为 L a =7.9mm， L b =8.6mm， L c =0.8mm， L s =30mm， W a =0.4mm， W b =0.3mm， W c =0.3mm，以及 W s =2.7mm。在参考平面的特征阻抗是50Ω。通过全波电磁场仿真提取得到的电路参数为 C ps 1 =1.7299pF, L ps 1 =0.6685nH, C ps 2 =1.9894pF, L ps 2 =0.1771nH, C p =0.136pF, L s 1 =-0.0845nH, L s 2 =0.4945nH。注意：对电路模型而言， L s 1为负值是完全许可的，这类似于具有负值的集总元件倒置器 [1] 。图2.49是用于测量的G形DMS实物照片，而图2.50所示为电路模型、全波电磁仿真与实际测量结果的比较。很显然，这三种结果吻合得非常好，这说明本小节提出的等效电路模型是正确的。
图2.49 实际制作的DMS传输线照片
图2.50 G形DMS的仿真与测量结果
2.3.5.4 结论
本小节提出了一种新颖的G形DMS，并讨论了它的阻带特性。通过改变该结构的几何尺寸，可以调整其频率响应。这里提出来针对具有新颖的G形DMS的修正平面传输线结构的等效集总电路模型，并通过实际制作该传输线进行测量。电路模型和全波电磁场仿真与实际测量结果吻合得很好。因此，本小节讨论的新型G-DMS，具有简单而又精确的等效电路模型，同时很容易通过全波电磁场仿真进行参数提取。可以预见，这类新型的DMS能够用于设计诸如双频带阻滤波器等双频段微波元器件。
