2.4 电阻器的连接

电路中的电阻要么以串联或并联的形式出现,要么以串并联的形式出现。通过电阻的串联、并联,可得到需要的电路网络,或得到所需阻值的电阻器。
 2.4.1 电阻器的串联
2.4.1 电阻器的串联

猴子捞月亮的故事你知道吧?那许多个猴子就是“串联”的形式。
若几个电阻首尾相接,如图2.29所示,就是电阻的串联。电阻串联后可等效为一个电阻(串联后的总电阻为R T ,如图2.29所示)。

图2.29 电阻器实物串联
结合2.3.1的知识,能否先看看上面三个电阻的阻值分别是多少?想一想,三个电阻串联后总电阻是多少?
图2.29所示是电阻器实物串联,从电路图上来看,则如图2.30所示。从上、下两图可以看到,相邻两个电阻器首尾相接是串联的要素。电阻器串联后,总电阻增大。总电阻等于所有串联在一起的电阻的阻值之和,用公式表示则为:


图2.30 串联电阻的电路图
需注意的是,两个串联电阻之间不能出现支路!若三个电阻连接到同一个节点,如图2.31所示,其中的R 1 与R 2 就不是串联关系。

图2.31 非串联电阻电路
例2.3:串联电阻的计算
 串联电阻电路有这样一个特点:在串联电阻电路中,流过每个电阻的电流一样;但每个电阻两端的电压不同。
串联电阻电路有这样一个特点:在串联电阻电路中,流过每个电阻的电流一样;但每个电阻两端的电压不同。
这个……需要怎样理解啊?
记住这个特点!
还记得前面2.1.2节中水管的例子吗?看图2.35所示的水管,以生活常识可知,a、b、c 三个位置处的水流量其实是一样的,但三处的水压不同。

图2.35 以水管类比串联电阻
根据生活常识即可知道,在同一时间内,被挤压的水管与未被挤压的水管内水流量是一样的。同理,串联电阻电路中,流过每一个电阻的电流一样。
很显然,当水管被挤压时,加在被挤压水管处的水压会更大些。即阻力小,水压就小;阻力大,水压就大。类比于串联电阻电路中每个电阻的电压,则电阻小,电阻两端的电压就小;电阻大,电阻两端的电压就大。利用欧姆定律很容易证明这个特点。
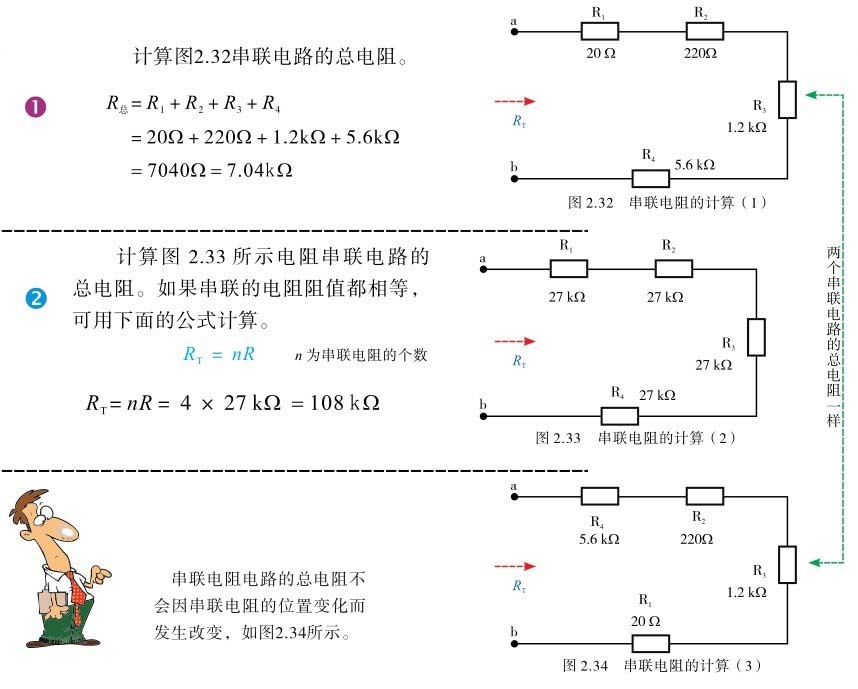
例2.4:计算图2.36所示的串联电阻电路中每个电阻的电流、每个电阻的端电压。先不要看解答的内容,请结合前面相关的知识尝试计算。如果可以的话,自己画一画它的电路图吧。

图2.36 例2.4图
解:在串联电阻电路中,流过每个电阻的电流可用式(2.8)计算。

 计算串联电阻电路的总电阻:R=R
1
+R
2
+R
3
=300Ω
计算串联电阻电路的总电阻:R=R
1
+R
2
+R
3
=300Ω
 计算串联电阻电路的电流:I=U÷R=3V÷300Ω=0.01A
计算串联电阻电路的电流:I=U÷R=3V÷300Ω=0.01A
 分别计算各电阻上的电压:U=IR
分别计算各电阻上的电压:U=IR

习题2.2:识别图2.37所示的三个色环电阻,并计算它们串联后的总电阻。

图2.37 三个色环电阻串联
习题2.3:在图2.38所示的电路中,R 2 的电流是多少?R 3 的电压是多少?

图2.38 习题2.3图
考察本节前面的内容可发现,串联电阻电路的总电压等于各串联电阻电压之和。或者说,加载到串联电阻电路的电压被按比例地分配到各串联电阻上,即串联电阻分压(见图2.39)。

图2.39 串联电阻分压
 2.4.2 电阻分压器
2.4.2 电阻分压器
从前一节的内容可知串联电阻电路的一个重要特点是,输入到串联电阻电路中的电压被分配到各串联电阻上。许多电路系统中的分压器其实就是利用了串联电阻电路的这个特点。
简单地说,分压器是一种在给定一个输入电压的情况下,将输入电压的一部分作为输出电压的电路。分压器是一种应用非常广泛的电子电路。

图2.40 电阻分压器电路
来看一看图2.40所示的电路,假设输出端未接其他任何电路,则流过 R 1 与R 2 的电流相同。从电路图中可以看到,V输出其实是取自电阻 R 2 两端的电压。结合前一节的内容可知,R 2 两端的电压可由式(2.9)计算:

从上面的公式与前一节的计算可知,串联电阻电路中每个电阻的电压总是小于输入电压。这意味着不论取串联电阻电路中哪个电阻的电压作为输出,分压器的输出电压总是小于输入电压,这就是被称为分压器的原因。
分压器常被用来从一个较大的电压中产生一个新的特定的电压。若输入电压不变、且分压器中电阻器的阻值是固定不变的,则分压器输出的电压也不变,人们常称其为固定分压电路,如图2.41所示。
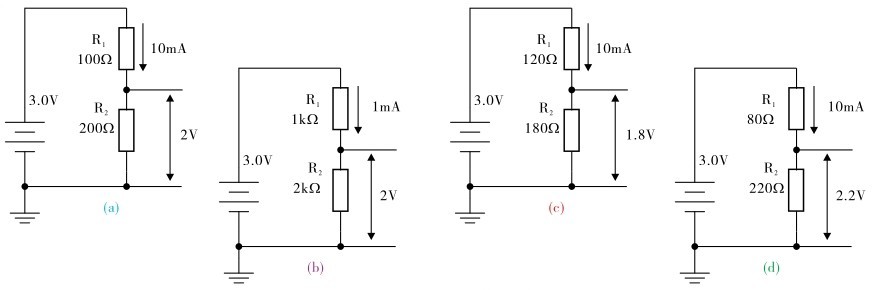
图2.41 固定分压电路
对于电阻分压器,有如下几种情况:
 若电阻分压器中任何一个电阻的阻值发生变化,分压器的输出电压随之变化,且电路中的电流会发生变化(可尝试自行计算)。
若电阻分压器中任何一个电阻的阻值发生变化,分压器的输出电压随之变化,且电路中的电流会发生变化(可尝试自行计算)。
 如果电阻分压器中的电阻按同一比例变化,则分压器的输出电压不变,但电路中的电流会发生变化。比较图2.41中的(a)、(b)。
如果电阻分压器中的电阻按同一比例变化,则分压器的输出电压不变,但电路中的电流会发生变化。比较图2.41中的(a)、(b)。
 若想使电阻分压器的输出电压减小,但电路中的电流不变,保持分压器总电阻不变的前提下,减小电阻 R
2
的阻值、增大 R
1
的阻值。比较图2.41中的(a)、(c)。
若想使电阻分压器的输出电压减小,但电路中的电流不变,保持分压器总电阻不变的前提下,减小电阻 R
2
的阻值、增大 R
1
的阻值。比较图2.41中的(a)、(c)。
 若想使分压器的输出电压增大,但电路中的电流不变,想想该怎么办?参阅图2.41中的(a)、(d)。
若想使分压器的输出电压增大,但电路中的电流不变,想想该怎么办?参阅图2.41中的(a)、(d)。
需注意的是,分压器规则总是假定输出电阻上是没有负载的。当输出电阻上有并联元件(负载)时,前面的分压器公式就不成立。幸好,接在分压器后面的大多数电路都是输入电路,而输入电路一般都是大阻值电路。当负载电阻大于输出电阻10倍以上时,许多人会忽略这个负载电路(虽然这会引起10%的误差)。
上面叙述中所说的R 1 、R 2 是泛指,并不指某个具体的电阻。R 2 是指分压电路中连接到“地”的电阻,另一个电阻则是 R 1 。在某些时候,电阻分压器电路中接“地”的电阻又称为下偏置电阻(不论电路电源的极性如何),未接地的电阻则被称为上偏置电阻。
 2.4.3 电阻器的并联
2.4.3 电阻器的并联
有过站队列的经历吧?
纵队好比串联,横排就好比并联。
若两个或几个电阻以头接头、尾接尾的方式连接在一起,如图2.42(b)所示,即是电阻的并联。电阻并联后可等效为一个电阻(并联后的总电阻,参见图2.42)。

图2.42 实物电阻器的并联
图2.42所示是电阻器实物并联,并联电阻电路如图2.43所示。从图2.42、图2.43 可以看到,电阻器头接头、尾接尾是并联的要素。电阻器并联后,总电阻减小。电阻并联后的总电阻R T 可利用下面的公式计算。如果只有两个电阻并联,用式(2.10)计算;若有三个或三个以上的电阻并联,用式(2.11)计算。

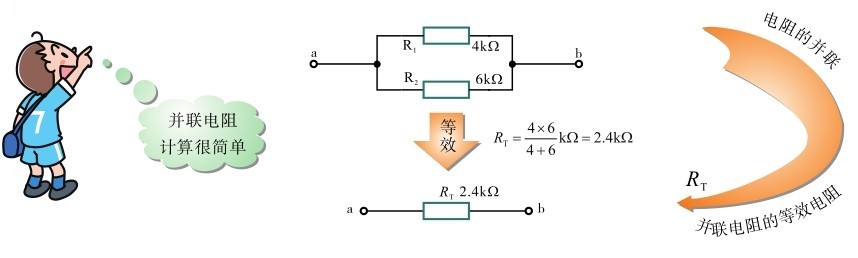
图2.43 并联电路图
例2.5:计算图2.44中两个并联电阻电路的总电阻。

图2.44 例2.5电路图

 若两个阻值相差10倍以上的电阻并联,并联后的总电阻近似等于阻值小的电阻。
若两个阻值相差10倍以上的电阻并联,并联后的总电阻近似等于阻值小的电阻。
 若 n 个阻值相同的电阻并联,并联后的总电阻等于单个电阻阻值的1/n。比如,两个100Ω的电阻并联后阻值为100÷2=50Ω四个 100 Ω的电阻并联后阻值为100÷4=25Ω。图2.45所示是一个电阻并联的计算技巧,图(a)中的3kΩ 电阻相当于由两个 6kΩ的电阻并联得到,如此,图(a)所示的电路可被理解为图(b)所示的电路——3 个 6kΩ 电阻并联的电路,其并联后的总电阻为6÷3=2kΩ。
若 n 个阻值相同的电阻并联,并联后的总电阻等于单个电阻阻值的1/n。比如,两个100Ω的电阻并联后阻值为100÷2=50Ω四个 100 Ω的电阻并联后阻值为100÷4=25Ω。图2.45所示是一个电阻并联的计算技巧,图(a)中的3kΩ 电阻相当于由两个 6kΩ的电阻并联得到,如此,图(a)所示的电路可被理解为图(b)所示的电路——3 个 6kΩ 电阻并联的电路,其并联后的总电阻为6÷3=2kΩ。

图2.45 电阻并联的计算技巧
 并联电阻电路有这样一个特点:在并联电阻电路中,每个电阻两端的电压一样,但流过每个电阻的电流不同。
并联电阻电路有这样一个特点:在并联电阻电路中,每个电阻两端的电压一样,但流过每个电阻的电流不同。
这个……需要怎样理解啊?
记住这个特点!
还记得水管类比电阻的例子吗?看图2.4所示的水管图例,很容易想象,主水管到各分支6水管的水压是一样的。但明显大水管阻力小,相当于小电阻;而小水管阻力大,相当于大电阻。

图2.46 用水管类比并联电路
根据生活常识即可知道,在同一时间内,各分支水管的水流量是不一样的。而主水管中的水流量等于各分支水管水流量之和。显然,各分支水管的水压是一样的。但是,分支水管管径大的水流量会大些,即阻力小,水流就大;阻力大,水流就小。类比于并联电阻电路中每个电阻的电流,则电阻小,流过电阻的电流就大;电阻大,流过电阻的电流就小。利用欧姆定律计算,可很容易证明并联电阻电路的这个特点。
例2.6:计算图2.47所示并联电阻电路的总电流、每个电阻的电流。☺如果可以的话,自己画一画它的电路图吧。
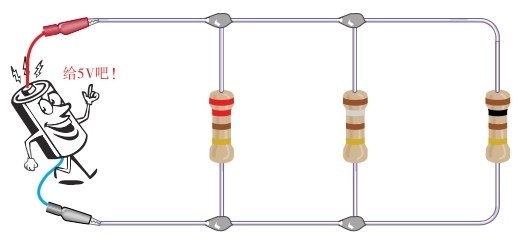
图2.47 例2.6图
 计算并联电阻电路的总电阻:
计算并联电阻电路的总电阻:

 计算并联电阻电路的总电流:
计算并联电阻电路的总电流:

 利用公式分别计算各电阻的电流。I=I
1
+I
2
+I
3
。
利用公式分别计算各电阻的电流。I=I
1
+I
2
+I
3
。
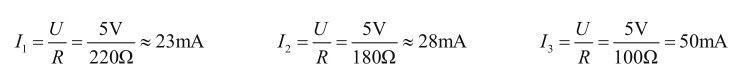
习题2.4:识别图2.48中的三个色环电阻,并计算它们并联后的总电阻。

图2.48 习题2.4图
习题2.5:已知图2.49中R 1 的电流为50mA,请计算 R 2 、R 3 的电流是多少?总电流是多少?

图2.49 习题2.5图
考察本节前面的内容可发现,并联电阻电路的总电流等于各并联电阻电流之和。或者说,加载到并联电阻电路的电流被按比例地分配到各并联电阻上,即并联电阻分流。如图2.50所示。
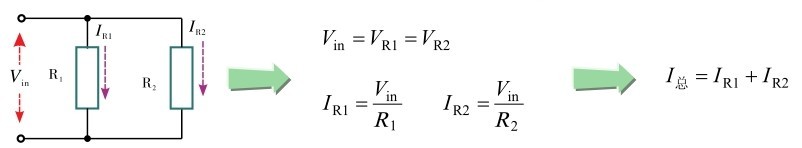
图2.50 并联电阻分流
前面所述的仅是一些基本的概念,在实际中应灵活运用。例如图2.51所示的电路,电路的总电流、总电阻可分别利用并联电阻计算公式、欧姆定律来计算。

图2.51 并联计算示例电路(1)
根据公式计算:

知道端电压的另一种计算方法:

在知道电路总电流I的情况下,可利用欧姆定律来计算纯并联电阻电路的分支电流。T 对于只有两个电阻并联的,可直接利用式(2.13)来计算电阻的电流:
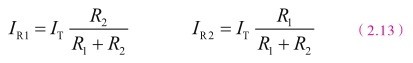
例如,假设并联的电阻电路及其参数如图2.52所示,则:

图2.52 并联计算示例电路(2)
电阻串联与并联的特性比较见表2.4。
表2.4 电阻串联与电阻并联的特性比较

 2.4.4 串-并联电路
2.4.4 串-并联电路
在实际电路中,电阻的串联和并联有时是同时存在的。计算电阻串联、并联共存的电路的总电阻并不复杂,简单地说就是化繁为简。对于一个串联、并联共存的电阻电路,只要把握住电阻串联、并联的特点,对每一个局部串联或并联先予以综合(计算局部的等效总电阻),即可很容易计算出复杂串联、并联共存的复合电路总电阻。以下通过示例进行说明。

图2.53 串并联共存的复合电路
这里用图解的方法解析图2.53中的
 、
、
 两个串并联电阻电路,如图2.54、图2.55所示,图2.53中余下的
两个串并联电阻电路,如图2.54、图2.55所示,图2.53中余下的
 、
、
 两个电阻电路请自行解析。
两个电阻电路请自行解析。
图2.53中
 的解析
的解析

图2.54 图2.53解析(1)
图2.53中
 的解析
的解析

图2.55 图2.53解析(2)
 2.4.5 实际与应用
2.4.5 实际与应用
电阻是应用最广泛的电子元件。电阻串联、并联电路是最基础的电路之一。仅仅是利用电阻串联、并联的知识即可实现许多实际应用,解决许多实际问题。最简单的就是通过串联、并联,利用手中现有的电阻得到自己所需要阻值的电阻器。下面来看两个简单的实际例子。
例2.7:有一个 110V、40W的灯泡,怎样将其接入220V的电路,灯泡才能正常工作?很显然,110V的灯具肯定不能直接用于220V的线路,否则灯泡会被烧毁。可以利用串联电阻分压的特性,在灯泡线路上串接一个合适的电阻,由串接的电阻分掉多余的电压。图2.56(a)是实物连接示意图,图2.56(b)则是电路原理图。
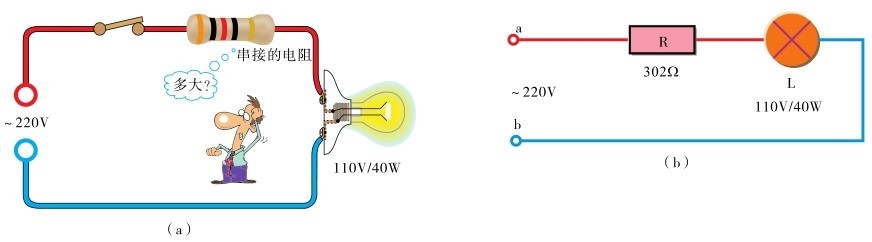
图2.56 例2.7图
灯泡的额定工作电压为110V,因此串接的电阻应分去的电压为
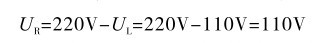
由灯泡的额定工作电压、额定功率可以计算出灯泡的额定工作电流为

由串联电路特性可知,串接电阻的电流I R 也为0.364A。据此,利用欧姆定律可计算出所串接电阻的阻值为
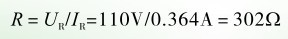
据计算结果可知,要 110V/40W的灯泡在220V电源上正常工作,需串接一个 302Ω的电阻。
例2.8:已知一个电流表的最大量程为100mA,已知一个电路的最大电流为1A。如何才能将这个电流表用于该电路的电流指示?
在用小量程表测量直流大电流时,可使用分流电阻器。分流电阻器与电流表并联,然后同时串联接入待测支路,如图2.57所示。
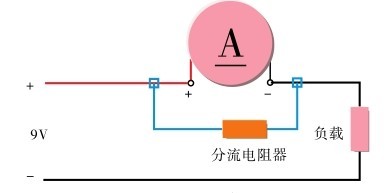
图2.57 例2.8图
图2.57所示为原理示意图。利用并联电阻分流的特性,在电流表上并联一个合适的电阻,即可扩大电流表的量程。
由题意可知,电阻器分流的电流为1A-100mA=900mA。
由欧姆定律可计算出分流电阻器的阻值为U/I=9V/0.9A=10Ω。
上面的叙述都没错,但不够完善,你发现了吗?电阻的基本物理特征是将电能转化为热能(参见 2.1.3 节的内容)。除考虑所用电阻的阻值外,还需考虑电阻的功率,否则可能出现电路故障或烧毁设备。
很明显,在例2.7中使用的电阻至少需要 40W的功率。在实际中,虽然串接这样一个电阻能解决问题,但通常用两个 110V、40W的灯泡(灯泡其实就是纯电阻负载)串接使用。
在例2.8中,分流电阻器可能会消耗 9V×0.9A=8.1W的功率。选用 10W的水泥电阻则可保证使用。
在电子设备电路系统中,电阻串联与并联的实际应用比比皆是。图2.58~图2.61所示的是四个实际的电路。图2.58~图2.60所示电路是典型的串联应用;图2.61所示的电路中既有串联又有并联,利用并联控制分压器输出,借以实现自动控制的目的。仔细观察并计算一下吧。
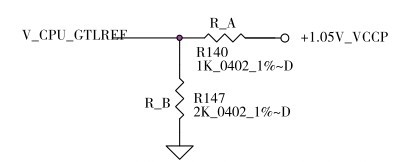
图2.58 戴尔笔记本电脑D620内的一个CPU参考电源电路
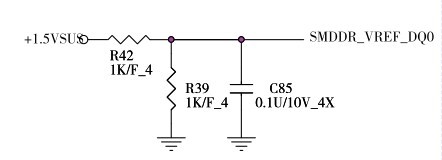
图2.59 东芝笔记本电脑L600内存储器的一个参考电源电路

图2.60 Nokia 206双卡手机中充电电路的一部分
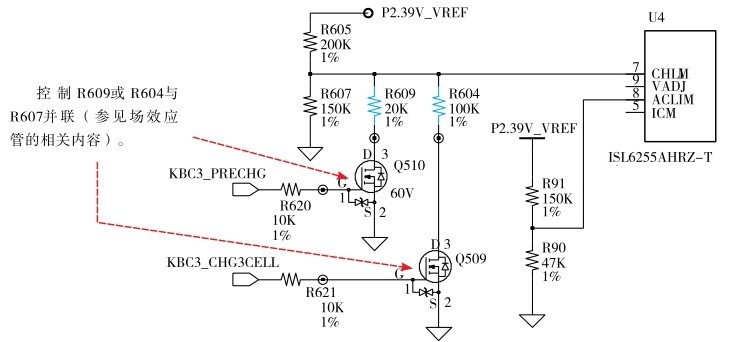
图2.61 三星笔记本电脑N220内充电控制器电路的一部分
 2.4.6 梯形电阻网络
2.4.6 梯形电阻网络
先看看图2.62所示的电阻串、并联电路的图形,像不像一架梯子呢?对啦,这就是称为梯形电阻网络的电阻串、并联网络的一种特殊形式。如果用电路图表示图2.62所示的电路,常见的为两种情况,如图2.63和图2.64所示。

图2.62 梯形电阻网络的电阻串、并联网络
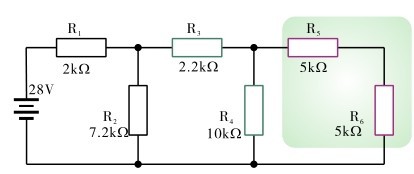
图2.63 梯形电阻网络电路图(1)
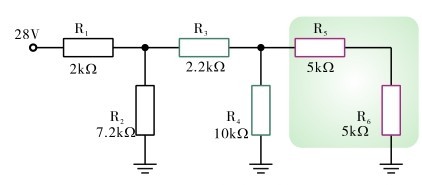
图2.64 梯形电阻网络电路图(2)
梯形电阻网络的级数可以是无限的,这里展示的是基本的三级梯形网络。这样一个梯形网络通常从等效总电阻、电压与电流三个方面进行分析。
从梯形网络的最后一级(离电源最远的一端)开始串联或并联简化,分解图如图2.65所示。最后得到上面的示例梯形网络等效总电阻为5.6kΩ。

图2.65 梯形电阻网络分解图
根据图2.65中的分解图
 可得到电路总电流:I=28V÷(2kΩ+3.6kΩ)=5mA。
可得到电路总电流:I=28V÷(2kΩ+3.6kΩ)=5mA。
得到电路总电流后,即可根据串、并联电路知识计算各分支电路的电流。图2.66所示是电路电流的分析示意图。你能否先计算一下呢?
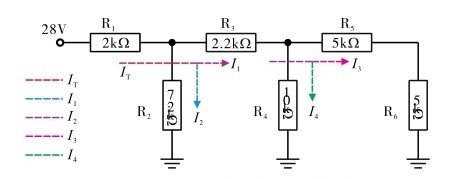
图2.66 电路电流的分析示意图
从上面的分析示意图中可以看到,很明显,I T =I 2 +I 3 +I 4 。
根据前一页图2.65的分解图
 可知,R
2
与等效电阻 R
t3
对 I
T
分流,得 I
1
与 I
2
;根据分解图
可知,R
2
与等效电阻 R
t3
对 I
T
分流,得 I
1
与 I
2
;根据分解图
 ,R
4
与等效电阻 R
t1
对I
1
分流,得 I
3
与I
4
。根据分流公式计算,可得
,R
4
与等效电阻 R
t1
对I
1
分流,得 I
3
与I
4
。根据分流公式计算,可得

根据上面的计算结果分析可知,R
1
的电流为5mA,R
3
、R
2
的电流为2.5mA,R
4
~R
6
的电流为1.25mA。知道了各个电阻的电流,利用欧姆定律当然可以很容易计算出电阻的电压。但这里的目的不在于此。你是否可以先利用分压公式计算?利用分压公式很容易计算出 R
1
的电压(参见前一页分解图
 )为10V,由此知 R
t4
的电压为28-10=18V。
)为10V,由此知 R
t4
的电压为28-10=18V。

R
t4
由R
2
//R
t3
得到(分解图
 ),因此,R
2
与 R
t3
的电压都为18V。
),因此,R
2
与 R
t3
的电压都为18V。
R
t3
由R
3
+R
t2
得到(分解图
 ),即 R
3
与R
t2
对 18V 分压。根据分压公式,可得V
R3
=5.5V ,V
Rt2
=12.5V 。
),即 R
3
与R
t2
对 18V 分压。根据分压公式,可得V
R3
=5.5V ,V
Rt2
=12.5V 。

到这里,已得到了 R 1 、R 2 、R 3 的电压,还剩下 R 4 、R 5 、R 6 的电压位置,请尝试参照上面的分析与电阻串联、并联的相关知识,求 R 4 、R 5 、R 6 的电压。
 2.4.7 惠斯通电桥
2.4.7 惠斯通电桥
学习电阻网络,自然需要了解惠斯通电桥(Wheatstone Bridge)。惠斯通电桥可用于精确测量电阻器的阻值,也可用于温度、压力等传感器电路,用于精确监测。例如,压力方面的液压控制压力传感器、涡轮增压压力传感器、大气压力传感器、轮胎压力传感器等。
图2.67所示是最常见惠斯通电桥的菱形结构。惠斯通电桥包含4个电阻、1个直流电源。菱形的顶角与底角连接直流电源。菱形两边角的A 点与 B 点为输出端。
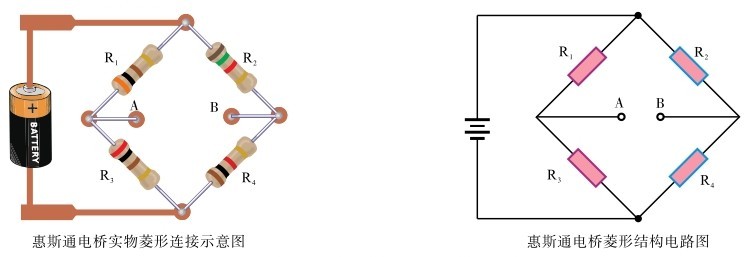
图2.67 最常见惠斯通电桥的菱形结构
图2.68所示是惠斯通电桥另一种形式的电路连接图,它清晰地展示了电阻之间的串、并联关系。

图2.68 惠斯通电桥另一种电路连接图
惠斯通电桥有平衡、不平衡两种状态。
当电桥的A、B 两点间电压为零时,电桥处于 。当电桥的A、B 两点间有电压时,平衡状态电桥处于不平衡状态。想一想,什么情况下,电桥的A、B 两点间电压为零。
很显然,当V A =V B 时,A、B 两点间的电压为零。结合串联电阻电路的知识,相信你能很容易明白如何才可以使 V A =V B 。据串联分压公式可知:

式(2.14)就是惠斯通电桥平衡的条件。
由上面的两个式子很容易得到其中任意一个电阻的表达式,例如:

其他3个电阻也可用相同的方法求出表达式。你试试?
可利用平衡惠斯通电桥求未知电阻
例2.9:如图2.69所示的电路:已知 R 1 ~R 3 的值,A、B 两点间的电压为零,求 R 4 的阻值。
V AB 为0,说明电桥处于平衡状态。根据上面的电桥平衡公式可得:

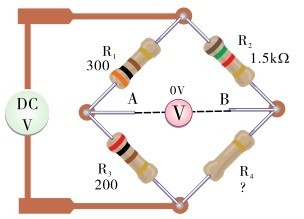
图2.69 例2.9图(1)
实际中,电桥中的两个电阻阻值固定,一个电阻为一个有刻度指示的可变电阻,电桥余下的一边留空,即图2.70中的C、D 端。C、D 端被用来接待测电阻,如图2.71所示。而电桥的A、B 端则连接探测器。探测器可以是电压表,也可以是电流表,通常是对任意方向电流都反应敏锐的电流表(μA级)。
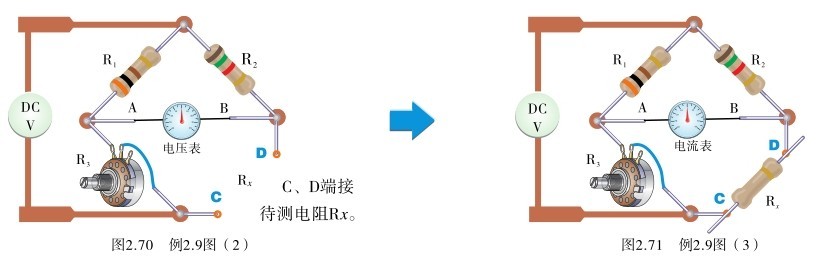

当待测电阻连接到电桥后,调节可调电阻 R 3 ,直到使电桥平衡,电流表显示为零,即 V A =V B 。此时可通过 R 3 的读数,利用电桥平衡公式计算出待测电阻 R x 的阻值。
例2.10:如图2.72所示的电路,已知 R 1 、R 2 的阻值如图所示,当R 3 的阻值调节到2.2kΩ时,电流表读数为零,求出R x 的值。
解:
电流表读数为零时电桥平衡,可通过式(2.14)得到R x 的计算公式为

将电路中的参数代入公式,计算得 R x 为495Ω。
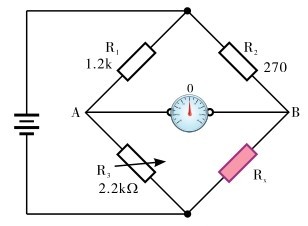
图2.72 例2.10图
前面所讲述的惠斯通电桥无疑是可以用于电阻测量的。但用于实际时还存在一些问题,不知你是否能发现?
如果 R 1 、R 2 固定,且 R 2 /R 1 =1,则电桥平衡时,待测电阻 R x 等于 R 3 。这意味着R 3 的调节范围必须覆盖 R x ,意味着 R 3 的调节范围必须很大,否则电桥不能平衡。例如,如果R x 为100kΩ,而R 3 的调节范围仅为47kΩ,则电桥永远不可能达到平衡。
因此,为了能在很宽的范围内覆盖待测电阻,必须能够改变 R 2 、R 1 ,如图2.73所示。在实际直流电桥测试仪中,R 1 、R 2 通常是由开关控制的值为10的幂的电阻组成的,如此,R 2 、R 1 按十进制数规律从 0.001 变化到1000。可变电阻 R 3 则通常为1Ω到11000Ω按整数调节。图2.74所示的就是一个商用直流电桥的面板图,从中可以看到按十进制规律调节的控制开关。

图2.73 可改变R 1 、R 2 的电路图

图2.74 商用直流电桥的面板图


