1.2 复杂电路的分析方法与规律
1.2.1 基本概念
在分析简单电路时,一般应用欧姆定律和电阻的串、并联规律,但用它们来分析复杂电路就比较困难。这里的简单电路通常是指只有一个电源的电路,而 复杂电路通常是指有两个 或两个以上电源的电路。 对于复杂电路,常用到基尔霍夫定律、叠加定理和戴维南定理进行分析。在了解这些定律和定理之前先来说明几个基本概念。
1.支路
支路是指由一个或几个元件首尾相接构成的一段无分支的电路。 在同一支路内,流过所有元件的电流相等。在图1-8所示的电路中,它有三条支路,即bafe支路、be支路和bcde支路。其中bafe支路和bcde支路中都含有电源,这种含有电源的支路称为有源支路。be支路没有电源,称为无源支路。
2.节点
三条或三条以上支路的连接点称为节点。 图1-8电路中的b点和e点都是节点。
3.回路
电路中任意一个闭合的路径称为回路。 图1-8电路中的abefa、bcdeb、abcdefa都是回路。
4.网孔
内部不含支路的回路称为网孔。 图1-8所示的电路中的abefa、bcdeb回路是网孔,abcdefa就不是网孔,因为它含有支路be。
1.2.2 基尔霍夫定律
基尔霍夫定律又可分为基尔霍夫第一定律(又称基尔霍夫电流定律)和基尔霍夫第二定律(又称基尔霍夫电压定律)。
1.基尔霍夫第一定律(电流定律)
基尔霍夫第一定律指出,在电路中,流入任意一个节点的电流之和等于流出该节点的电 流之和。 下面以图1-9所示的电路来说明该定律。
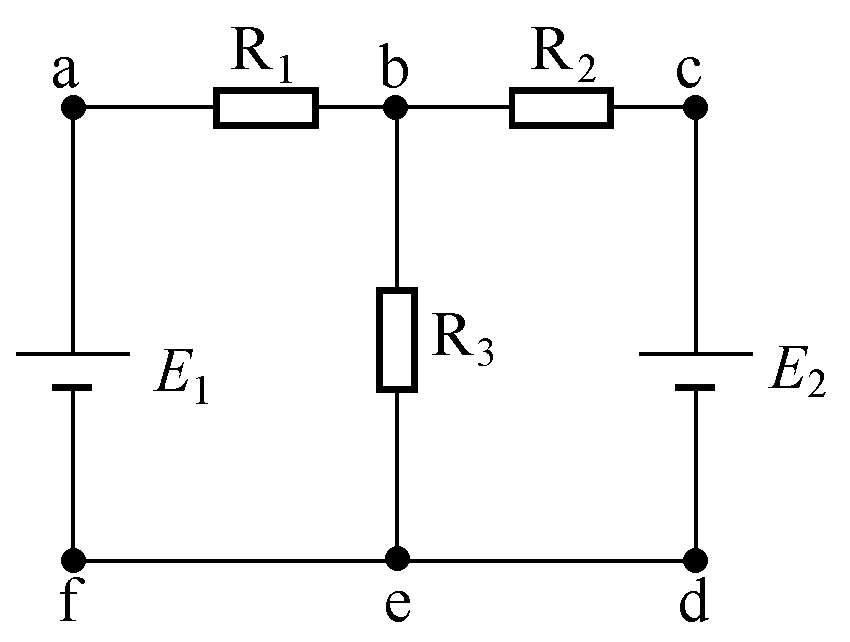
图1-8 一种复杂电路
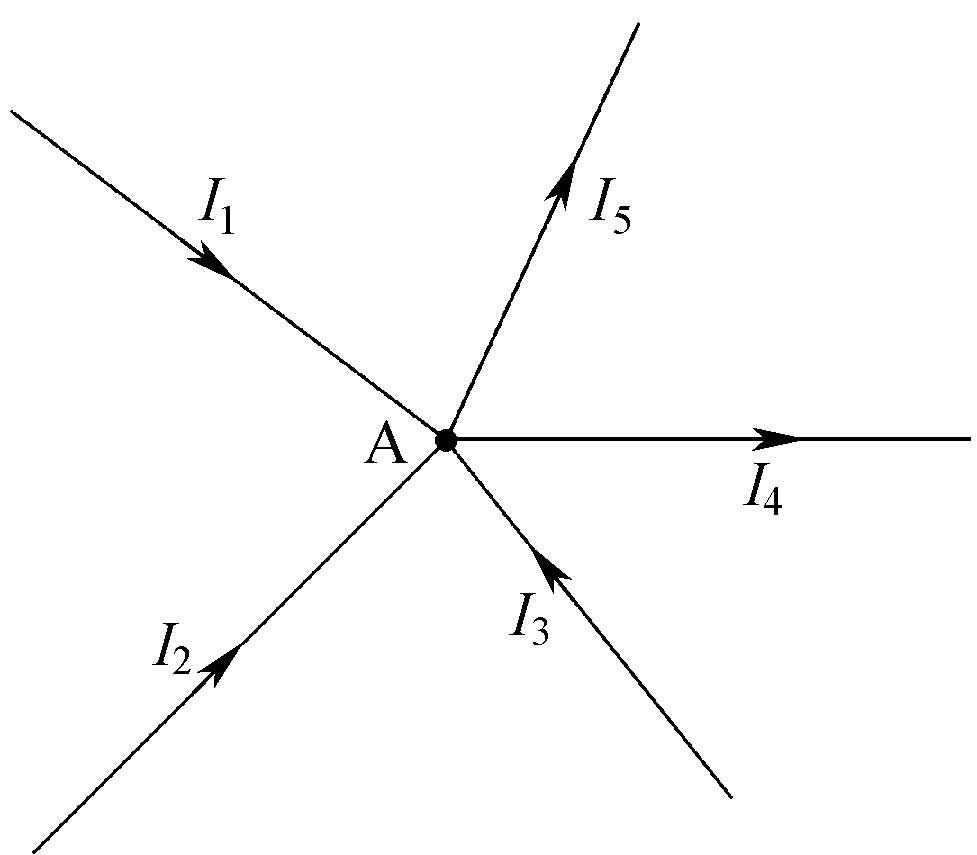
图1-9 节点电流示意图
在图1-9电路中,流入A点的电流有 I 1 、 I 2 、 I 3 ,从A点流出的电流有 I 4 、 I 5 ,由基尔霍夫第一定律可得
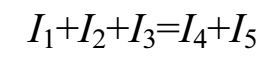
又可表示为
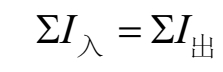
这里的“Σ”表示求和,可读作“西格马”。
如果规定流入节点的电流为正,流出节点的电流为负,那么基尔霍夫第一定律也可以这样叙述:在电路中任意一个节点上,电流的代数和等于零,即
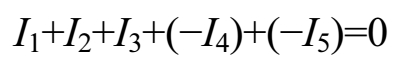
也可以表示成
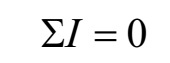
基尔霍夫第一定律不但适合于电路中的节点,对一个封闭面也是适用的。 如图1-10所示,图1-10(a)中流入晶体管的电流 I b 、 I c 与流出的电流 I e 有以下关系:
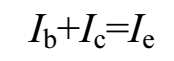
在图1-10(b)中,流入三角形负载的电流 I 1 与流出的电流 I 2 、 I 3 有以下关系:
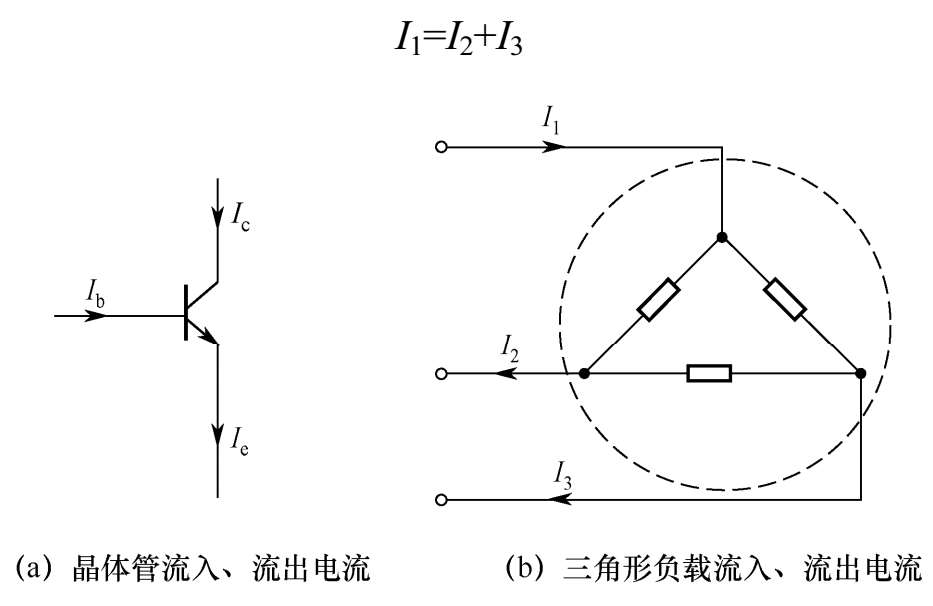
图1-10 封闭面电流示意图
2.基尔霍夫第二定律(电压定律)
基尔霍夫第二定律指出,电路中任意回路内各段电压的代数和等于零, 即
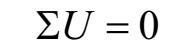
在应用基尔霍夫第二定律分析电路时,需要先规定回路的绕行方向,当流过回路中某元件的电流方向与绕行方向一致时,该元件两端的电压取正,反之取负;当电源的电动势方向(电源的电动势方向始终是由负极指向正极)与绕行方向一致时,电源的电动势取负,反之取正。下面以图1-11所示的电路来说明这个定律。
先来分析图1-11电路中的BCDF回路的电压关系。首先在这个回路中画一个绕行方向,流过R 2 的电流 1 2 和流过R 3 的电流 1 3 与绕行方向一致,故 1 2 R 2 (即为 U 2 )和 1 3 R 3 (即为 U 3 )都取正,电源的电动势 E 2 方向与绕行方向一致,电源的电动势 E 2 取负,根据基尔霍夫电压定律可得出
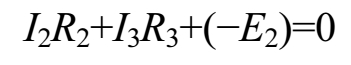
再来分析图1-11所示电路中的ABFH回路的电压关系。先在ABFH回路中画一个绕行方向,流过R 1 的电流 1 1 方向与绕行方向相同, 1 1 R 1 取正,流过R 2 的电流 1 2 方向与绕行方向相反, 1 2 R 2 取负,电源 E 2 的电动势方向(负极指向正极)与绕行方向相反, E 2 取正,电源 E 1 电动势方向与绕行方向相同, E 1 取负,根据基尔霍夫第二定律可得出
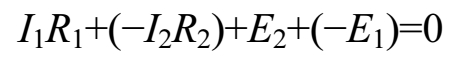
3.基尔霍夫定律的应用——支路电流法
对于复杂电路的计算常常要用到基尔霍夫第一、第二定律,并且这两个定律经常会同时使用,下面介绍应用这两个定律计算复杂电路的一种方法——支路电流法。
支路电流法使用时的一般步骤是:
① 在电路上标出各支路电流的方向,并画出各回路的绕行方向。
② 根据基尔霍夫第一、第二定律列出方程组。
③ 解方程组求出未知量。
下面举例说明支路电流法的应用。
如图1-12所示为汽车照明电路,其中 E 1 为汽车发电机的电动势, E 1 =14V,R 1 为发电机的内阻, R 1 =0.5Ω, E 2 为蓄电池的电动势, E 2 =12V,R 2 为蓄电池的内阻, R 2 =0.2Ω,照明灯电阻 R =4Ω,求各支路电流 I 1 、 I 2 、 I 和加在照明灯上的电压 U R 。
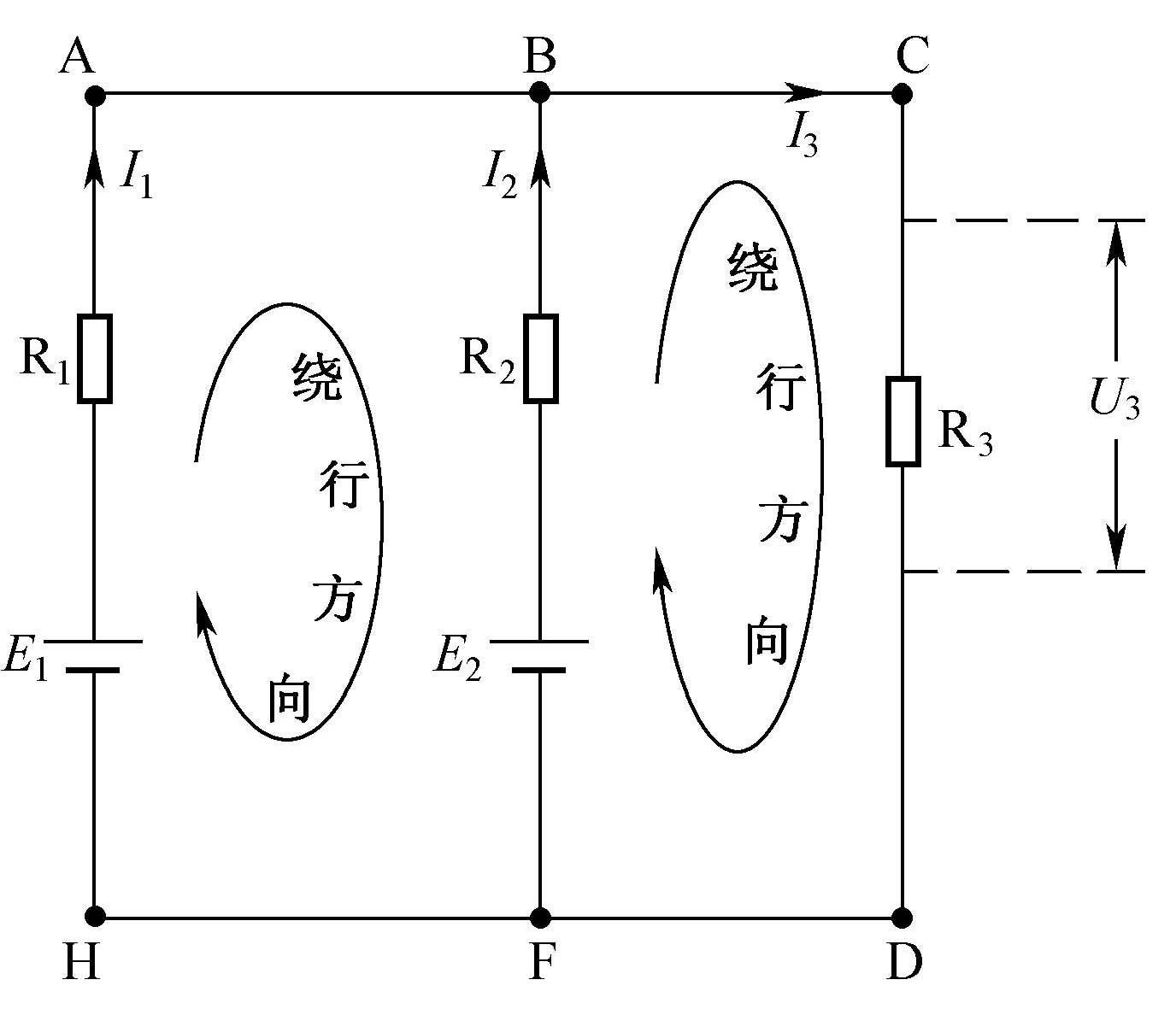
图1-11 基尔霍夫第二定律说明图
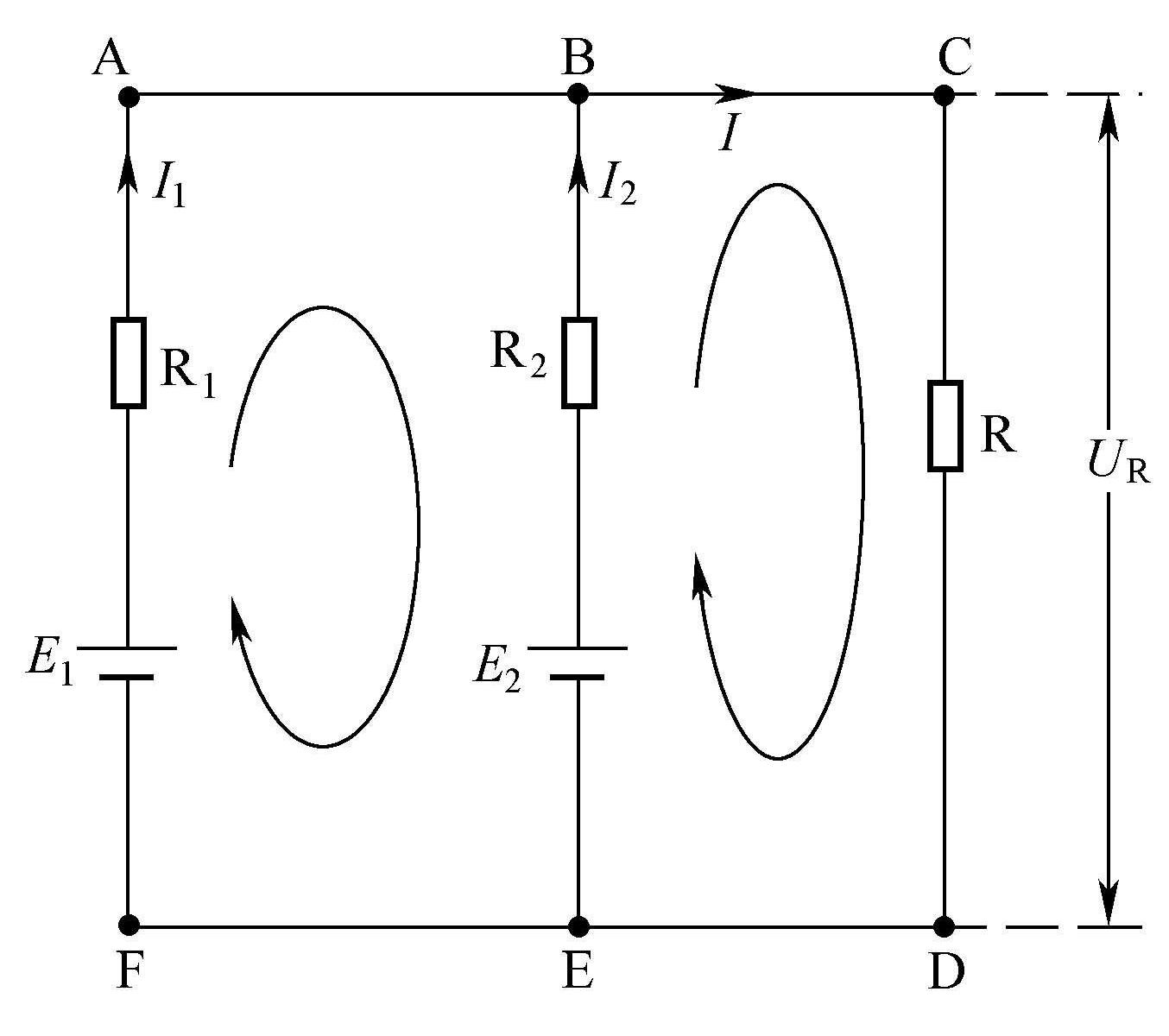
图1-12 汽车照明电路
解题过程如下:
第一步:在电路中标出各支路电流 I 1 、 I 2 、 I 的方向,并画出各回路的绕行方向。
第二步:根据基尔霍夫第一、第二定律列出方程组。
节点B的电流关系为
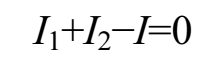
回路ABEF回路电压关系为
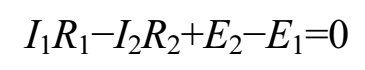
回路BCDE回路电压关系为
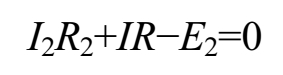
第三步:解方程组。
将 E 1 =14V, R 1 =0.5Ω, E 2 =12V, R 2 =0.2Ω代入上面三个式子中,再解方程组可得
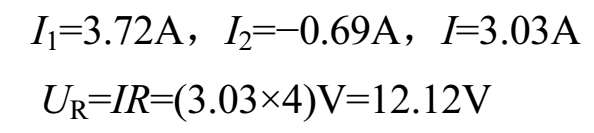
上面的 I 2 为负值,表明 I 2 电流实际方向与标注方向相反,即 I 2 电流实际是流进蓄电池的,这说明发电机在为照明灯供电的同时还对蓄电池进行充电。
1.2.3 叠加定理
对于一个元件,如果它两端电压与流过的电流成正比,这种元件就被称为线性元件,线 性电路是由线性元件组成的电路, 电阻就是一种最常见的线性元件。 叠加原理是反映线性电 路基本性质的一个重要原理。
叠加原理的内容是:在线性电路中,任意支路中的电流(或电压)等于各个电源单独作 用在此支路中所产生的电流(或电压)的代数和。
下面以求图1-13(a)所示的电路中各支路电流 I 1 、 I 2 、 I 的大小来说明叠加定理的应用,图中的 E 1 =14V, R 1 =0.5Ω, E 2 =12V, R 2 =0.2Ω, R =4Ω。
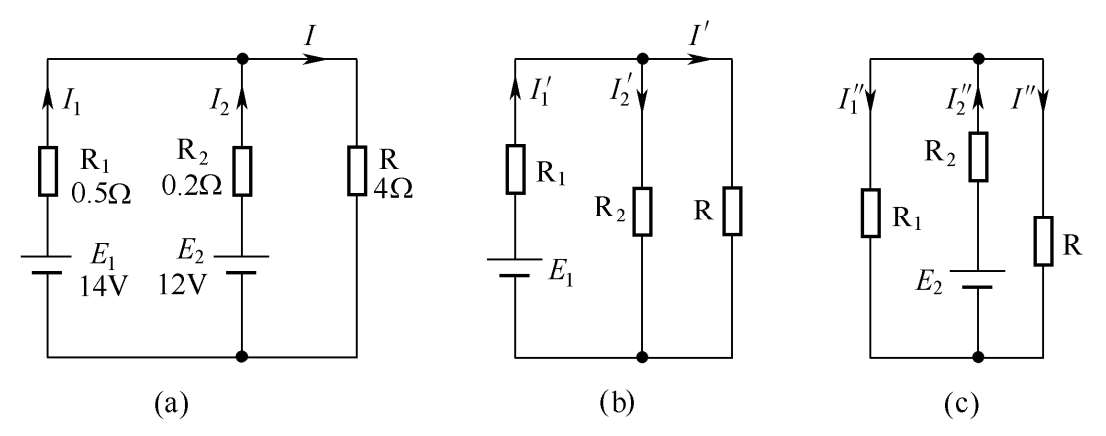
图1-13 利用叠加定理求支路电流
解题过程如下:
第一步:在图1-13(a)所示的电路中标出各支路电流的方向。
第二步:画出只有一个电源 E 1 作用时的电路,把另一个电源当作短路,并标出这个电路各支路的电流方向,如图1-13(b)所示,再分别求出该电路各支路的电流大小,即
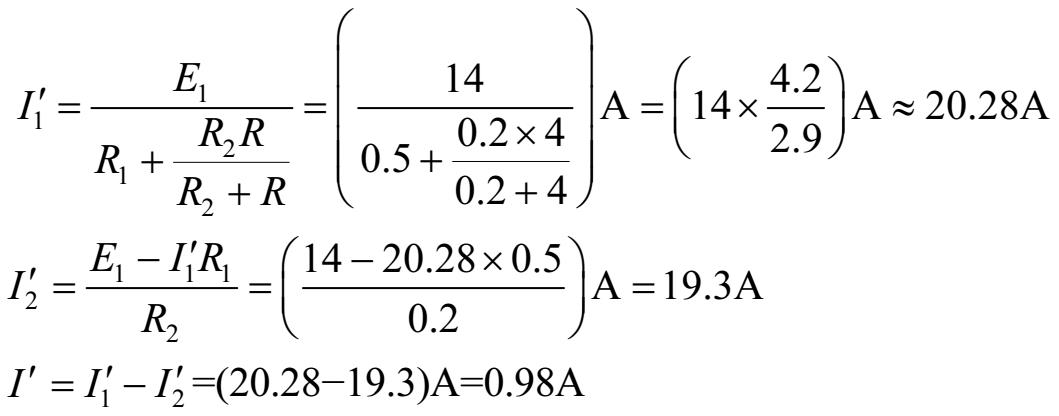
第三步:画出只有电源 E 2 作用时的电路,把电源 E 1 当作短路,并在这个电路中标出各支路电流的方向,如图1-13(c)所示,再分别求出该电路各支路的电流大小,即
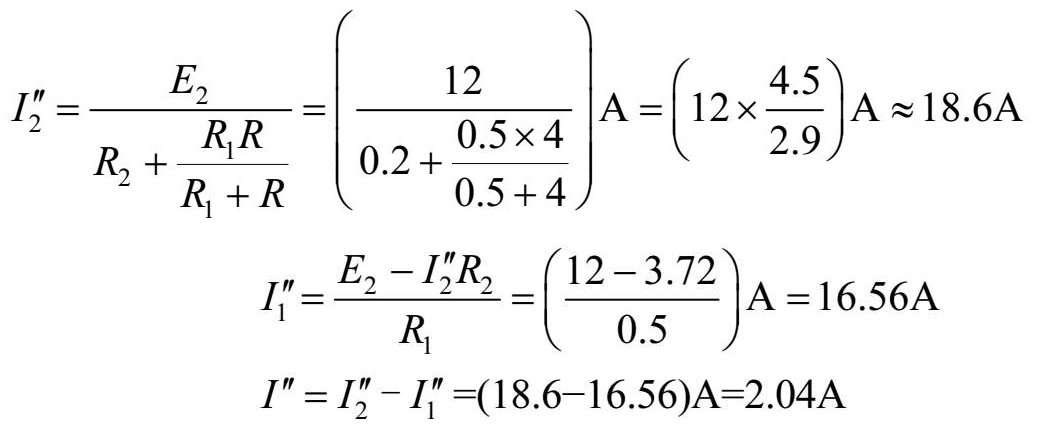
第四步:将每一支路的电流或电压分别进行叠加。凡是与电路图1-13(a)所示中假定的电流(或电压)方向相同的为正,反之为负。这样可以求出各支路的电流分别是
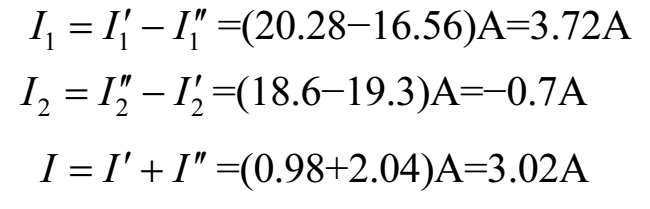
1.2.4 戴维南定理
对于一个复杂电路,如果需要求多条支路的电流大小,则可以应用基尔霍夫定律或叠加定理。如果仅需要求一条支路中的电流大小,则应用戴维南定理更为方便。
在介绍戴维南定理之前,先来说明一下二端网络。 任何具有两个出线端的电路都可 以称为二端网络。包含电源的二端网络称为有源二端网络,否则就叫作无源二端网络。 图1-14(a)所示电路就是一个有源二端网络,通常可以将它画成图1-14(b)所示的形式。
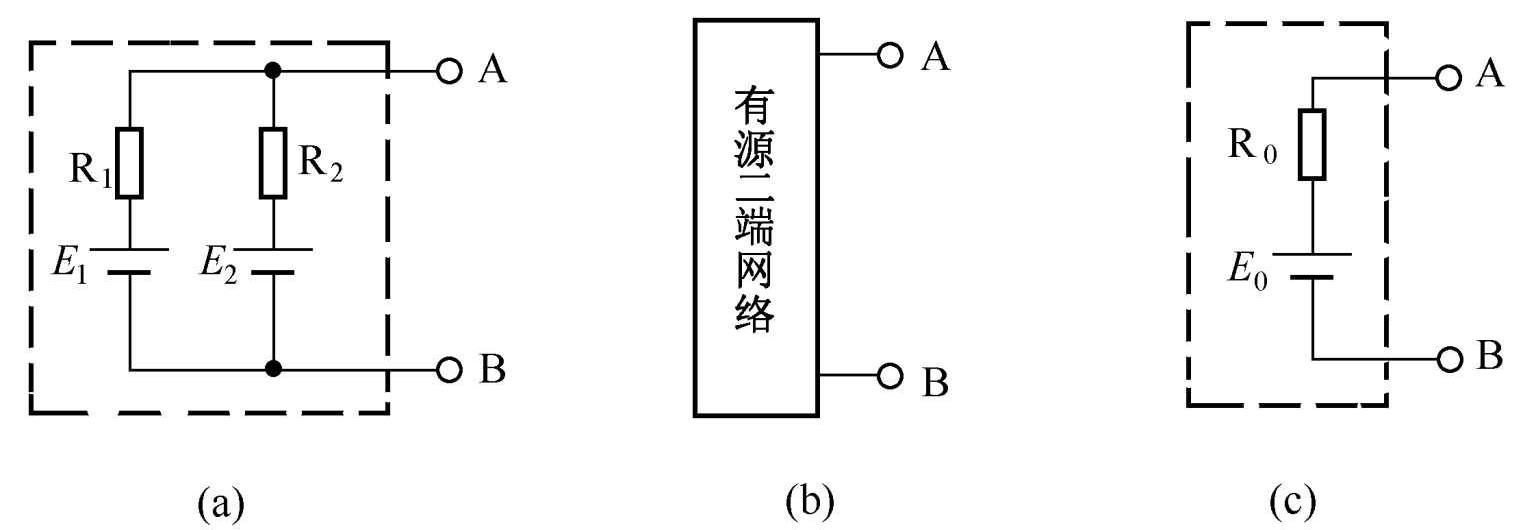
图1-14 有源二端网络
戴维南定理的内容是:任何一个有源二端网络都可以用一个等效电源电动势 E 0 和内阻R 0 串联起来的电路来代替。 根据该定理可以将图1-14(a)所示的电路简化成图1-14(c)所示的电路。
那么等效电源电动势 E 0 和内阻R 0 如何确定呢? 戴维南定理还指出:等效电源电动势 E 0 是该有源二端网络开路时的端电压;内阻R 0 是指从两个端点向有源二端网络内看进去,并 将电源均当成短路时的等效电阻。
下面以图1-15所示的电路为例来说明戴维南定理的应用。在图1-15(a)所示的电路中, E 1 =14V, R 1 =0.5Ω, E 2 =12V, R 2 =0.2Ω, R =4Ω,求流过电阻R的电流 I 的大小。
解题过程如下:
第一步,将电路分成待求支路和有源二端网络,如图1-15(a)所示。
第二步,假定待求支路断开,求出有源二端网络开路的端电压,此即为等效电源电动势 E 0 ,如图1-15(b)所示,即
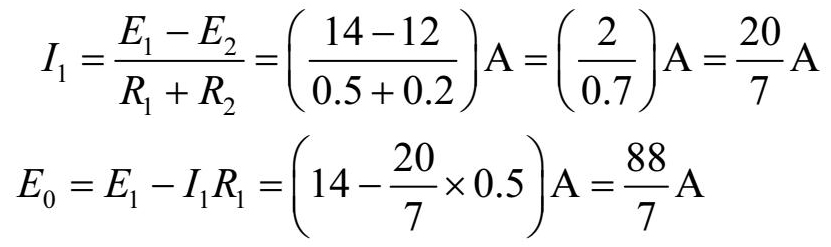
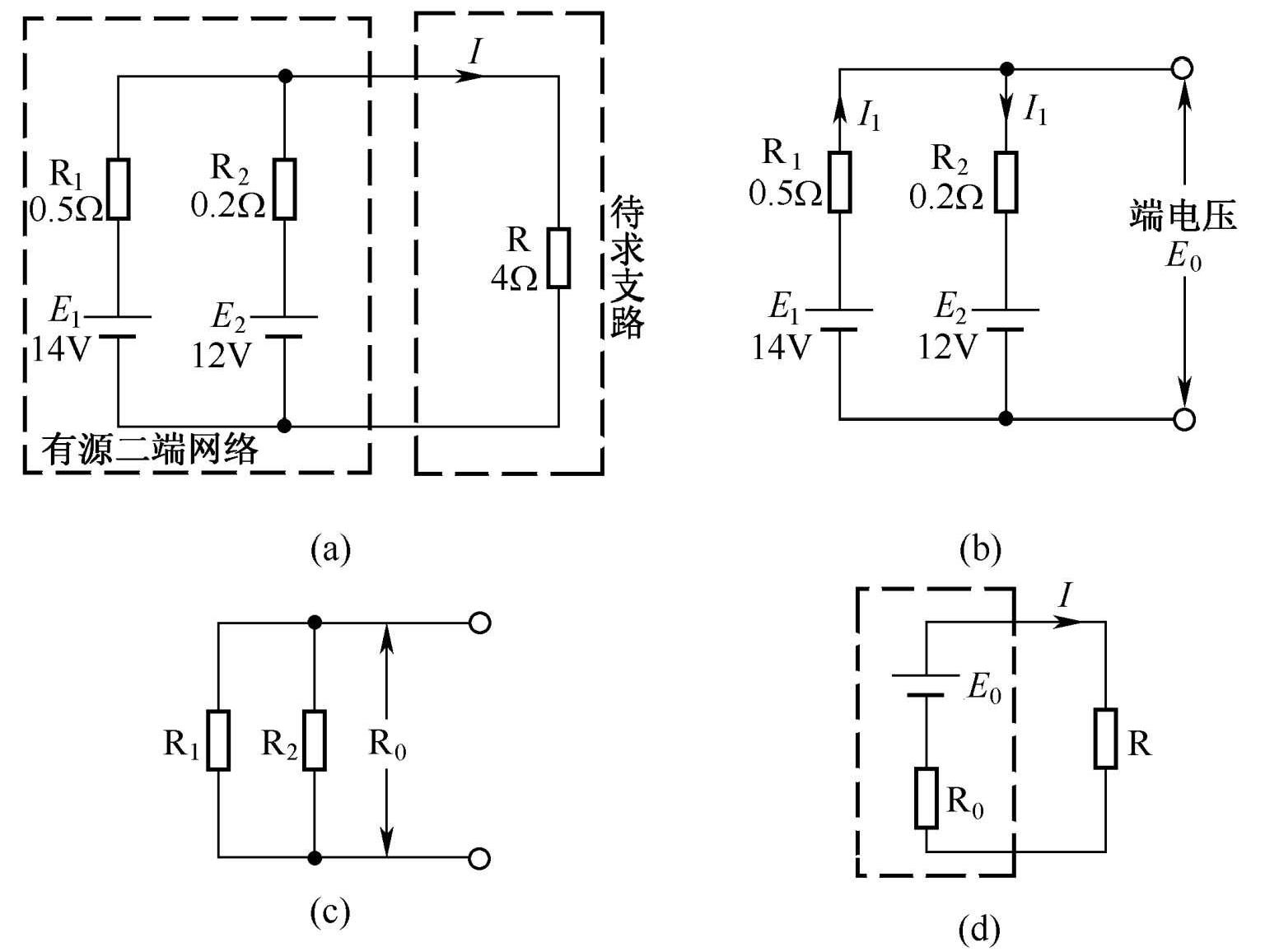
图1-15 用戴维南定理求支路电流
第三步,假定有源二端网络内部的电源都短路,求出内部电阻,此即为内阻 R 0 ,如图1-15(c)所示,即
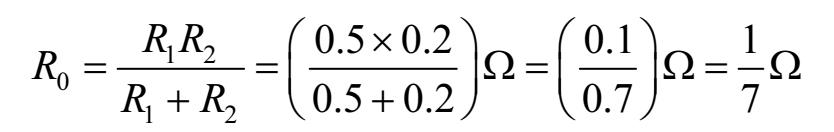
第四步,画出图1-15(a)电路的戴维南等效电路,如图1-15(d)所示,再求出待求支路电流的大小,即
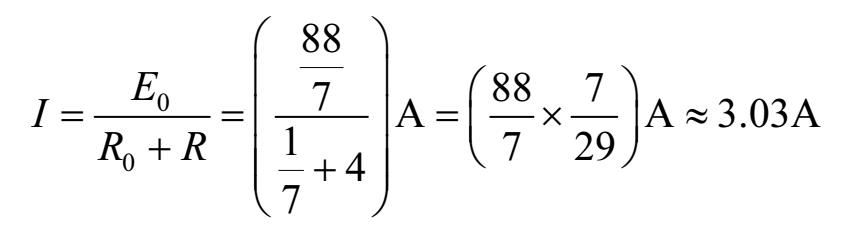
1.2.5 最大功率传输定理与阻抗变换
1.最大功率传输定理
在电路中,往往希望负载能从电源中获得最大的功率。怎样才能做到这一点呢?如图1-16所示, E 为电源的电动势,R为电源的内阻,RL为负载电阻, I 为流过负载RL的电流, U 为负载两端的电压。
负载R
L
获得的功率
 。当增大R
L
的阻值时,电压
U
会增大,但电流
I
会减小;如果减小R
L
的阻值,虽然电流
I
会增大,但电压
U
会减小。什么情况下功率
P
的值最大呢?
最大功率传输定理内容是:负载要从电源获得最大功率的条件是负载的电阻(阻抗)与电源
的内阻相等。
负载的电阻与电源的内阻相等又称两者阻抗匹配。在图1-16所示的电路中,负载R
L
要从电源获得最大功率的条件是
R
L
=
R
,此时R
L
得到的最大功率是
。当增大R
L
的阻值时,电压
U
会增大,但电流
I
会减小;如果减小R
L
的阻值,虽然电流
I
会增大,但电压
U
会减小。什么情况下功率
P
的值最大呢?
最大功率传输定理内容是:负载要从电源获得最大功率的条件是负载的电阻(阻抗)与电源
的内阻相等。
负载的电阻与电源的内阻相等又称两者阻抗匹配。在图1-16所示的电路中,负载R
L
要从电源获得最大功率的条件是
R
L
=
R
,此时R
L
得到的最大功率是
 。
。
如果有多个电源向一个负载供电,如图1-17所示,负载R
L
怎样才能获得最大功率呢?这时,要先用戴维南定理求出该电路的等效电阻
R
0
和等效电动势
E
0
,只要
R
L
=
R
0
,负载就可以获得最大功率
 。
。
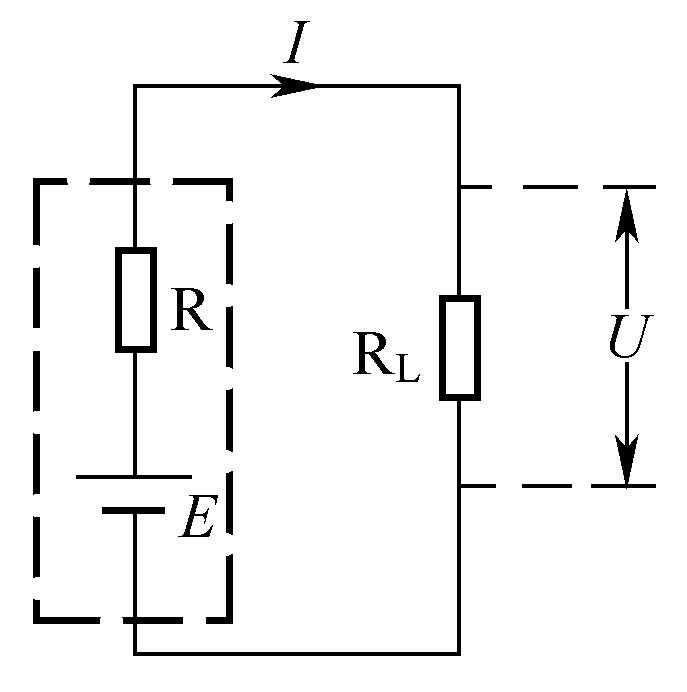
图1-16 简单电路功率传输
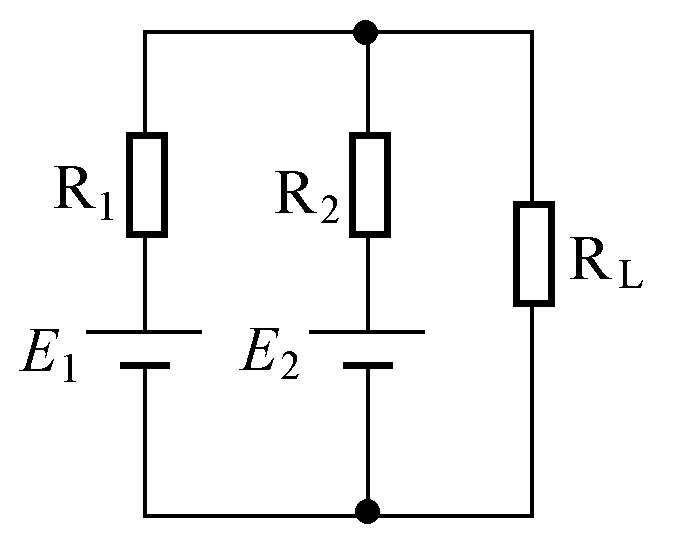
图1-17 复杂电路功率传输
2.阻抗变换
当负载的阻抗与电源的内阻相等时,负载才能从电源中获得最大功率,但很多电路的负载阻抗与电源的内阻并不相等,这种情况下怎么才仍能让负载获得最大功率呢?解决方法是进行阻抗变换, 阻抗变换通常采用变压器。 下面以图1-18所示电路为例来说明变压器的阻抗变换原理。
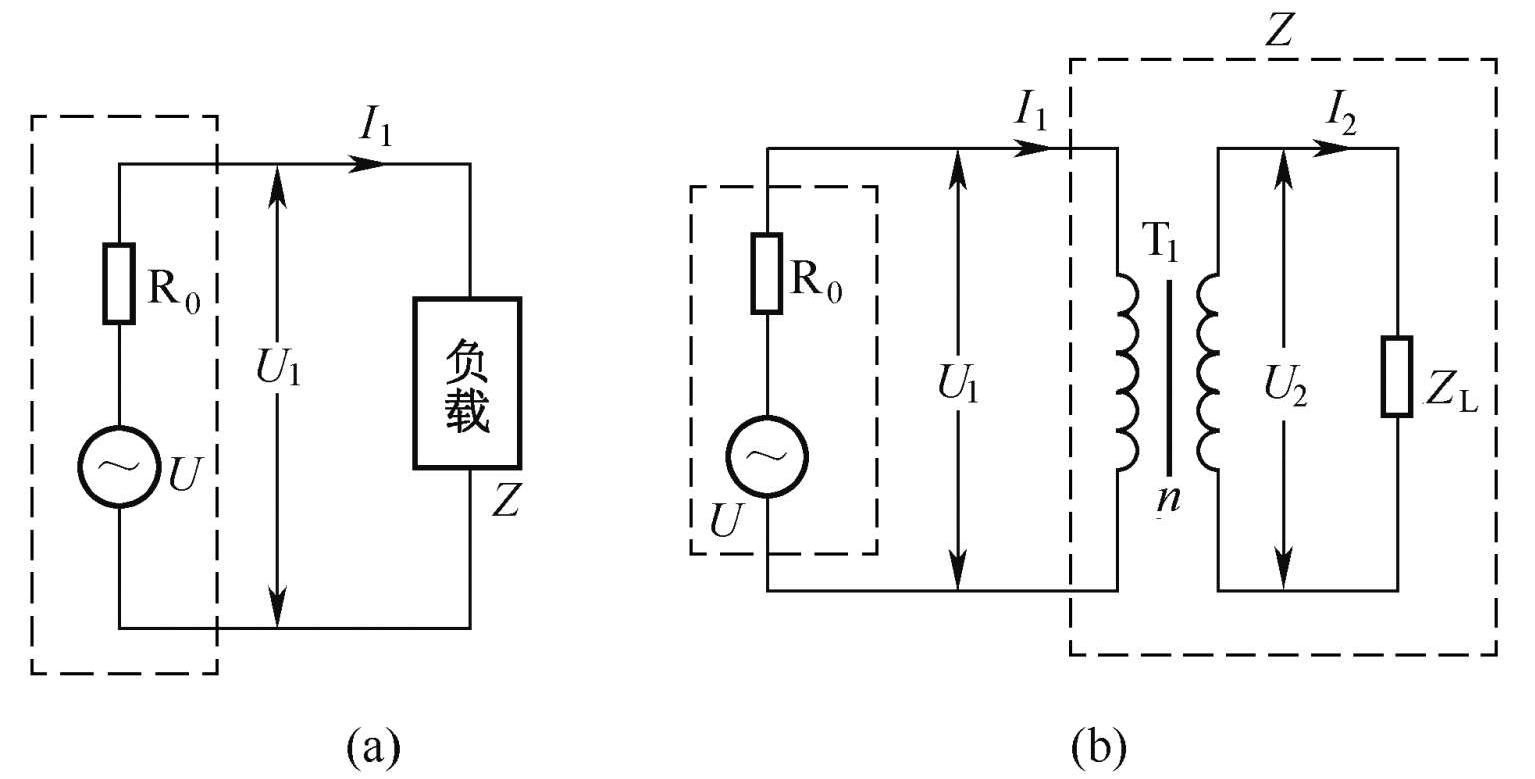
图1-18 变压器的阻抗变换原理说明图
在图1-18(a)中,要负载从电源中获得最大功率,需让负载的阻抗
Z
与电源(这里为信号源)内阻
R
0
相等,即
Z
=
R
0
,这里的负载可以是一个元件,也可以是一个电路,它的阻抗可以用
 表示。
表示。
现假设负载是图1-18(b)虚线框内由变压器和电阻组成的电路,该负载的阻抗
 ,变压器的匝数比为
n
,电阻的阻抗为
Z
L
,根据变压器改变电压的规律
,变压器的匝数比为
n
,电阻的阻抗为
Z
L
,根据变压器改变电压的规律
 可得到下式,即
可得到下式,即
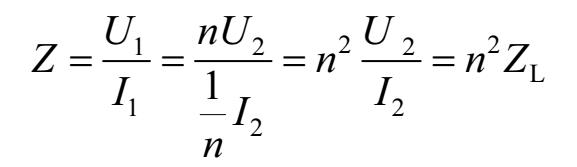
从上式可以看出,变压器与电阻组成电路的总阻抗 Z 是电阻阻抗 Z L 的 n 2 倍,即 Z = n 2 Z L 。如果让总阻抗 Z 等于电源的内阻 R 0 ,则变压器和电阻组成的电路就能从电源获得最大功率;又因为变压器不消耗功率,所以功率全传送给真正负载(电阻),达到功率最大限度传送的目的。由此可以看出: 通过变压器的阻抗变换作用,真正负载的阻抗不须与电源内阻相等, 同样能实现功率最大传输。
下面举例来说明变压器阻抗变换的应用。如图1-19所示,音频信号源内阻 R 0 =72Ω,而扬声器的阻抗 Z L =8Ω,如果将两者按图1-19(a)的方法直接连接起来,扬声器将无法获得最大功率。这时,可以在它们之间加一个变压器T 1 ,如图1-19(b)所示,至于选择匝数比 n 为多少的变压器,可用 R 0 = n 2 Z L 来计算,结果可得到 n =3。也就是说,只要在两者之间接一个 n =3的变压器,扬声器就可以从音频信号获得最大功率,从而发出最大的音量。
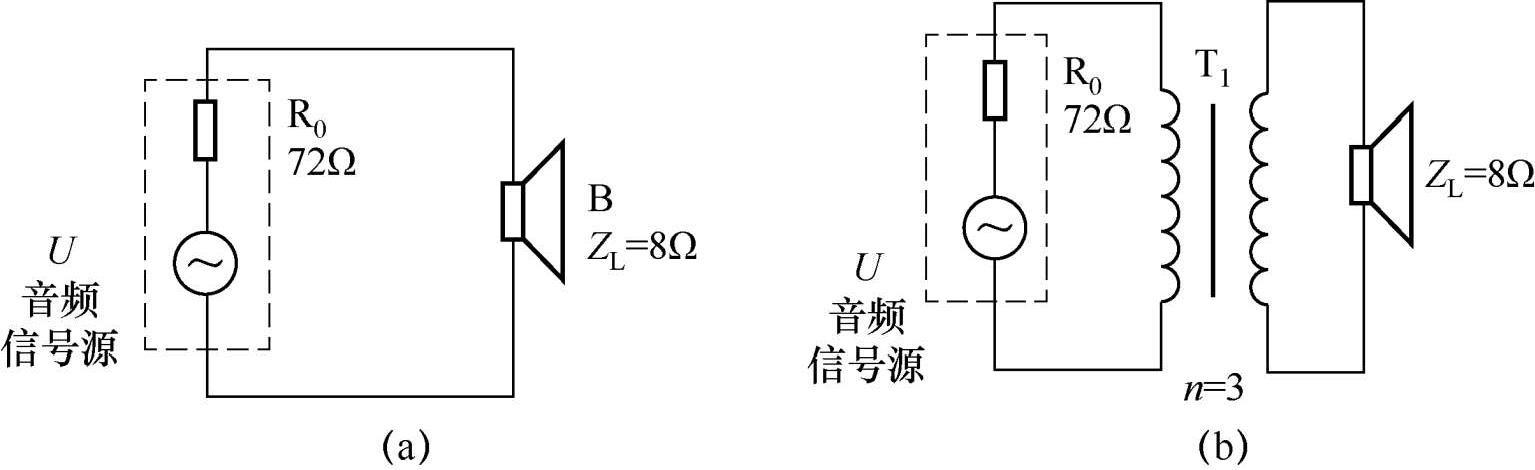
图1-19 变压器阻抗变换举例


