第四节
视听关联研究新进展——从七言律诗到《孙子定理》

对视听关联与通感研究，笔者苦于手头无可资参考的材料，长期难深入进行。终于在2003年教学和课余研究过程中有了新的转机：

一、教育教学研究信息

高等师范院校公共《教育学》教材在阐述教学方法的演示法时提供了一个研究数据：

研究表明，人们从外界获得的信息中，来自视觉的占83%，听觉占11%，嗅觉占3.5%，触觉和味觉分别是1.5%和1.0%。当视听觉结合时，其学习材料的保持率远远高于单一视觉和听觉的保持率。可见教学演示要考虑各种感官的合理组合与巧妙运用。 ^[2]

人们从外界获得的信息中，视觉占83%，听觉占11%。这个数据很重要。笔者将在下文阐述、分析。

二、数论研究信息

2012年，天津商业大学数学教授吴振奎老先生赠给我几本他自己写的书，有一本新出版的《数学中的美》（哈尔滨工业大学出版社，2011年1月第一版），该书第171页有这样一段话：

1875年鲁卡斯（E.Lucas）在《新数学年鉴》征求以下问题解答

1 ² +2 ² +3 ² +……+x ² =y ²

仅有x=24，y=70的非平凡解（x=0，±1为平凡解）。

这个貌似平常的问题，直到1876年布兰克（M.Blanc）才给出一个证明，转年卢卡斯指出证明的一个漏洞，而后再无下文。

40年后，1918年瓦尔特森（G.N.Watson）给出了一个有14页长的证明，且动用了高深的椭圆函数工具。

1952年德国数学家吕格林（W.Ljunggren）将证明作了简化（利用四次扩域中的Pell方程）。

直到1985年德莫根（DeMorgang）才给出一个初等证法，此后亦有我国的马德刚等人也给出一个初等证法（同年）。

1990年安格林（W.S.Anglin）给出一个更简洁的初等证法。

吴振奎教授讲道：“我们感兴趣的是等式1 ² +2 ² +……+24 ² =70 ² 本身，这让我们立刻联想到用边长是1～24正方块去拼装边长为70的大正方形问题，结论并不让人太失望，人们经过努力给出了一个24块仅剩一块（边长为7）的拼法。”

笔者对此也有一个联想，更令人对中国古代乐律学和天文历法感兴趣和神往……并且有个更简洁的证明，暂不公布。

适当时候，笔者将在另外一本书里具体分析说明。并对仅剩一块7有一个不同与众的分析——这个与1/49相关联……

三、视听通感分析概略

正常人获得信息量视觉占83%，前述怪圈总数和为411。这个83就是笔者在“怪圈”里求得的。

而且，这个83也与中国古代的五音宫（81）、徵（108）、商（72）、羽（96）、角（64）密切关联。五音是通过“三分损益律”求出其数值的，但管仲并未在《管子·地员》里透露是如何得到宫音的。

可以肯定地说，在春秋大政治家和哲学家管仲生活的公元前7世纪的中国，一些高级知识分子知道二进制，并且能很熟练地使用！

这个问题，通过当代人类对地球的认识变得越来越清晰。

可以说，对地球的一些重要数据不了解就不知道宫音81的含义。对“大衍环”和“怪圈”不了解也就不知道81和64是如何求得的。

正是通过83把视觉与听觉联系起来了。

——五音长度之和：

81+108+72+96+64=421。而421是第83号非合数。

83+421=504=220+284=241+263.

我们知道，“怪圈”的总和是411。

411=3×137；3与137分别是第3和第34号非合数。因此，411的素秩SZ=（3+3）+（34+137）=177=3×59；3与59分别是第3与第18号非合数。因此，177的素秩：

SZ=（3+3）+（18+59）=83.

而中国古代哲学里，把58认为是“观”——即观察。观察就是视觉对外部世界有目的、有计划、比较持久的知觉。

但，我们如何才能知道58（观）就与视觉获得外界信息相关呢？

通过查阅笔者编制的《非合数位序表》，可知第58号非合数是269。亦即非合数269在58号位序上。

269=10 ² +13 ² 。这里10+13=23；23与58的二进制是一对逆序数。

（58） ₁₀ =（111010） ₂ 逆序数（010111） ₂ =（23） ₁₀

前述，269=10 ² +23 ² ，而第10与第13号非合数是23与37。

因为，第58（观）号非合数是269。

因此，269的A=（10+23）+（13+37）=83。

83 ² =6889；叠加6889为：68+89=157；再叠加：1+57=58（归位）。

即：观察是出于一种需要，观察与83有关。按现在的研究说，就是人的83%的信息是通过视觉获得的。

但，我们又如何知道听觉与视觉相互关联呢？

我们知道，五音的长度是宫81、徵108、商72、羽96、角64。而五音长度之和：

∑=81+108+72+96+64=421。

另一方面，五音长度数值的逆序数之和为：

∑=18+801+27+69+46=961=31 ² 。

而五音长度之和为421。421=14 ² +15 ² 。第14与第15号非合数是41与43。因此，有：

A=（14+41）+（15+43）=113。又113恰好是第31号非合数。

因此，有：31+113=144=12 ² 。

即有：12+12=24。而第24号非合数是83。但24可以得到随38。

即，求1+2+3+……+24=300。300必然是个三角形数。

因而有：8×300+1=2401=49 ² ；而叠加2401有：24+01=25。

25 ² =625；6+25=31；31 ² =961；961 ² =923521；叠加有：

923+521=1444=38 ² 。而叠加1444为：14+44=58。

故，非合数421归到序数58上。同时也表明，视觉与听觉关联。

四、从七言律诗到《孙子定理》

因为，83属于4k+3型质数，根据法国业余数学家费尔马的分析，83这样的质数至少需要有三个以上的整数平方和表达。

这里，83=3 ² +5 ² +7 ² 。

而七言律诗的最常见的是第3、第5、第7句不押韵脚。

又，3+5+7=15。第3、5、7号非合数是3、7、13。即：

3+7+13=23。因此就有：15+23=38。

这样，我们找到了可以同时表达38与83的一组数：3、5、7以及第3、5、7号非合数是3、7、13。

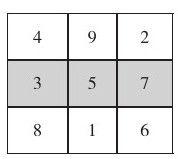
而非合数3、5、7又恰好处于《洛书》三阶幻方的第二行。

而第3、第5、第7号非合数是3、7、13。

3+7+13=23。由此，我们可能要重新认识《孙子定理》里关于“今有物不知其数”。

《孙子定理》“物不知数”：

“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”

这相当于求解一次同余式组

N≡2（mod3）≡3（mod5）≡2（mod7）

《孙子算经》未提出一般原理，仅给出具体问题的解法：

“三、三数之，剩二，置一百四十；五、五数之，剩三，置六十三；七、七数之，剩二，置三十。并之，得二百三十三。以二百一十减之，即得。凡三、三数之剩一，则置七十；五五数之剩一，则置二十一；七、七数之，则置十五。一百六以上，以一百五减之，即得。”

《孙子算经》给出的答数，符合条件的正数解是N=23；事实上，对于符合此条件的数还有128，233……等。

分析：

所要求的数N应该是5和7的倍数，同时被3除后余2；是3和7的倍数，同时被5除后余3；是3和5的倍数，同时被7除后余2。同时满足上述三个条件的最小之数。

剖析：

是5和7的倍数，同时被3除后余1的数是70；则余2的数就是70×2=140；是3和7的倍数，同时被5除后余1的数是21，则余3的数就是21×3=63；是3和5的倍数，同时被7除后余1的数是15，则余2的数即是15×2=30。

因此，N=70×2+21×3+15×2-105×2=233-210=23。

在《易经》的成卦法中，50根蓍草经三变二十一演而必得下列四种可能策数之一：

4×9=36，4×8=32，4×7=28，4×6=24.

“非经精密的数学计算或反复试验，不可能得到如此机巧之构思。这种机巧，从数论来看正是同余式理论的思想。” ^[3] 我们在这里要说的是，50根蓍草经三变结果的四种可能策数分别是四的九、八、七、六倍。九、八、七、六四个数被称为“四营数”。而36被称为“太阳”，24被称为“太阴”，28被称为“少阳”，32被称为“少阴”。

笔者在这里需要特别说明的是，6、7、8、9作为序数，其对应的非合数分别是11、13、17、19。

6+7+8+9=30；11+13+17+19=60.

30:60=1:2.

1:2在乐律学上就是纯八度。

同样是关于“同余式”的问题，则先后出现在《周易》和《孙子算经》里，这让人感到比较有意思。而关于“物不知数”符合条件的最小正数解为23。

虽然《孙子算经》被定为公元4世纪的作品，但它最著称于世的是其下卷的“物不知数”，（此问题可能还有更远的源流）。

中国最早是在历法的上元积年计算中运用到同余式问题的。

后来，宋代的数学家秦九韶发现了《周易》筮法的同余式结构，找到了同余式问题的渊源，并在此问题上引导出了求解一次同余组的一般解法——“大衍求一术”。现代数学文献一般把求解一次同余组的剩余定理称为“中国剩余定理”，或称作“孙子定理”。当然，在中国民间对此还有称“剪管术”“秦王暗点兵”“韩信点兵”等。

更令人称奇的是，按“C规则”运算，23一步即进入“大衍环”。

“大衍环”的总数为1621。1621展开以后其“数字根”为64，但对1621的二进制叠加以后，数值为46。如下：

1621=25×64+21；Y=25+21=46。即：

（1621） ₁₀ =（011001010101） ₂ ；叠加011001010101为：

（011001+010101） ₂ =（101110） ₂ =（46） ₂

23是精子或卵子的染色体数目，46是受精卵的染色体数目。

因此，我们需要重新认识与评价“物不知数”的深远意义……

五、对数论研究的另一种认识

已知，1 ² +2 ² +3 ² ……+x ² =y ² 。有非平凡解x=24；y=70。

而从第1号非合数1开始，把非合数一一加起来，一直加到第24号非合数83，和为875。即：

∑=1+2+3+5+7+11+13+17+19+……+83=875

正向叠加有：8+75=83。（第24号非合数也是83）。

（875在“大衍环”里，上部9个特征数的“众数和”为83）。

而875在“大衍环”里，其数字根之和则为38。

亦即，前24个非合数装满了“大衍环”的上半球。而在天文历法里，一年有24节气。