第2章 密码学基础与应用
2.1 密码学的基本概念
密码学(Cryptology)是一门古老的科学。大概自人类社会出现战争便产生了密码,以后逐渐形成一门独立的学科。在密码学形成和发展的历程中,科学技术的发展和战争的刺激都起了积极的推动作用。电子计算机一出现便被用于密码破译,使密码进入电子时代。1949年香农(C.D.Shannon)发表了《保密系统的通信理论》的著名论文,把密码学置于坚实的数学基础之上,标志着密码学作为一门科学的形成。1976年W.Diffie和M.Hellman提出公开密钥密码,从此开创了一个密码新时代。1977年美国联邦政府颁布数据加密标准(DES),这是密码史上的一个创举。1994年美国联邦政府颁布密钥托管加密标准(EES),1994年美国联邦政府颁布数字签名标准(DSS),2001年美国联邦政府颁布高级加密标准(AES)。我国国家密码管理局一直高度重视密码标准管理工作,从2000年就开始组织相关规范的组织编写工作,先后用白皮书的形式发布了系列技术标准,规范了商用密码产品的研发与应用。2011年,经国标委批准设立了密码行业标准化技术委员会,标志着密码标准化工作正式纳入到国家标准管理体系。目前,我国许可并大力推广应用的通用密码算法是SM2椭圆曲线公钥密码算法、SM3密码杂凑算法和SM4分组密码算法。同时,在智能电网、居民健康卡、社会保障等领域允许使用SM1分组密码算法,在电子标签、重要门禁系统等领域采用SM7分组密码算法,在通信领域采用ZUC祖冲之密码算法。这些都是密码发展史上的一个个重要的里程碑。
研究密码编制的科学称为 密码编制学 (Cryptography),研究密码破译的科学称为 密码分析学 (Cryptanalysis),密码编制学和密码分析学共同组成 密码学 (Cryptology)。
密码学作为信息安全的关键技术,其安全目标主要包括三个非常重要的方面: 保密性 (confidentiality)、 完整性 (integrity)和 可用性 (availability)。
2.1.1 密码学的基本安全目标
2.1.1.1 保密性
保密性是确保信息仅被合法用户访问,而不被泄露给非授权的用户、实体或过程,或供其利用的特性。即防止信息泄漏给非授权个人或实体,信息只为授权用户使用的特性。这里的“访问”是指不仅可以读,还能浏览、打印或简单了解一些特殊资源是否存在。
常用的保密技术包括:防侦收(使对手侦收不到有用的信息)、防辐射(防止有用信息以各种途径辐射出去)、数据加密(在密钥的控制下,用加密算法对信息进行加密处理。即使对手得到了加密后的信息也会因为没有密钥而无法读懂有效信息)、物理保密(利用各种物理方法,如限制、隔离、掩蔽、控制等措施,保护信息不被泄露)等。
2.1.1.2 完整性
完整性是指所有资源只能由授权方或以授权的方式进行修改,即信息未经授权不能进行改变的特性。信息在存储或传输过程中保持不被偶然或蓄意地删除、修改、伪造、乱序、重放、插入等破坏和丢失的特性。完整性是一种面向信息的安全性,它要求保持信息的原样,即信息的正确生成和正确存储和传输。
完整性与保密性不同,保密性要求信息不被泄露给未授权的人,而完整性则要求信息不致受到各种原因的破坏。影响网络信息完整性的主要因素有:设备故障、误码(传输、处理和存储过程中产生的误码,定时的稳定度和精度降低造成的误码,各种干扰源造成的误码)、人为攻击、计算机病毒等。
2.1.1.3 可用性
可用性是指所有资源在适当的时候可以由授权方访问,即信息可被授权实体访问并按需求使用的特性。信息服务在需要时,允许授权用户或实体使用的特性,或者是网络部分受损或需要降级使用时,仍能为授权用户提供有效服务的特性。可用性是信息系统面向用户的安全性能。信息系统最基本的功能是向用户提供服务,而用户的需求是随机的、多方面的、有时还有时间要求。可用性一般用系统正常使用时间和整个工作时间之比来度量。
可用性还应该满足以下要求:身份识别与确认、访问控制(对用户的权限进行控制,只能访问相应权限的资源,防止或限制经隐蔽通道的非法访问)。
2.1.2 密码体制
密码技术的基本思想是伪装信息,使未授权者不能理解它的真实含义。所谓伪装就是对数据进行一组可逆的数学变换。伪装前的原始数据称为 明文 (Plaintext),伪装后的数据称为 密文 (Ciphertext),伪装的过程称为 加密 (Encryption)。加密在 加密密钥 (Key)的控制下进行。用于对数据加密的一组数学变换称为 加密算法 。发信者将明文数据加密成密文,然后将密文数据送入网络传输或存入计算机文件,而且只给合法收信者分配密钥。合法收信者接收到密文后,施行与加密变换相逆的变换,去掉密文的伪装恢复出明文,这一过程称为 解密 (Decryption)。解密在 解密密钥 的控制下进行。用于解密的一组数学变换称为 解密算法 ,而且解密算法是加密算法的逆。因为数据以密文形式在网络中传输或存入计算机文件,而且只给合法收信者分配密钥。这样,即使密文被非法窃取,因为未授权者没有密钥而不能得到明文,因此未授权者也不能理解它的真实含义,从而达到确保数据秘密性的目的。同样,因为未授权者没有密钥也不能伪造出合理的明密文,因而篡改数据必然被发现,从而达到确保数据真实性的目的。与能够检测发现篡改数据的道理相同,如果密文数据中发生了错误或毁坏也将能够检测发现,从而达到确保数据完整性的目的。
一个密码系统,通常简称为 密码体制 (Cryptosystem),由五部分组成(如图2-1)。
(1) 明文空间 M,它是全体明文的集合。
(2) 密文空间 C,它是全体密文的集合。
(3) 密钥空间 K,它是全体密钥的集合。其中每一个密钥K均由加密密钥K e 和解密密钥K d 组成,即K=<K e ,K d >。
(4) 加密算法 E,它是一族由M到C的加密变换。
(5) 解密算法 D,它是一族 由C到M 的解密变换。
对于每一个确定的密钥,加密算法将确定一个具体的加密变换,解密算法将确定一个具体的解密变换,而且解密变换就是加密变换的逆变换。对于明文空间M中的每一个明文M,加密算法E在密钥K e 的控制下将明文M加密成密文C:
C=E(M,K e ) (2-1)
而解密算法D在密钥K d 的控制下将密文C解密出同一明文M:
M=D(C,K d )=D(E(M,K e ),K d ) (2-2)
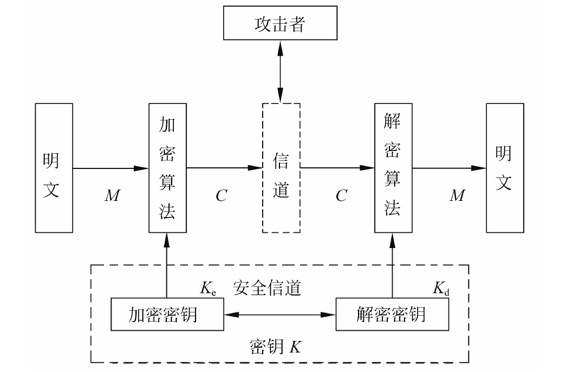
图2-1 密码体制
如果一个密码体制的K d =K e ,或由其中一个很容易推出另一个,则称为 单密钥密码体制 或 对称密码体制或传统密码体制 。否则称为 双密钥密码体制 。进而,如果在计算上K d 不能由K e 推出,这样将K e 公开也不会损害K d 的安全,于是便可将K e 公开。这种密码体制称为 公开密钥密码体制 ,简称为 公钥密码体制 。公开密钥密码体制的概念于1976年由W.Diffie和M.Hellman提出。它的出现是密码发展史上的一个里程碑。
如果能够根据密文系统地确定出明文或密钥,或者能够根据明文-密文对系统地确定出密钥,则我们说这个密码是 可破译 的。研究密码破译的科学称为密码分析学。
密码分析者攻击密码的方法主要有以下三种。
(1) 穷举攻击。 所谓穷举攻击是指,密码分析者采用依次试遍所有可能的密钥对所获得的密文进行解密,直至得到正确的明文;或者用一个确定的密钥对所有可能的明文进行加密,直至得到所获得的密文。显然,理论上,对于任何实用密码只要有足够的资源,都可以用穷举攻击将其攻破。从平均角度讲,采用穷举攻击破译一个密码必须试遍所有可能密钥的一半。
值得注意的是,如果分析者不得不采用穷举攻击时,他们往往会首先尝试那些可能性最大的密钥。例如,基于用户为了容易记忆往往会选择一些短的数据或有意义的数据作为口令(如姓名、生日、电话号码、邮件地址等)这样的事实,黑客在攻击用户口令时往往首先尝试这些短的和有意义的口令。这一事实告诉我们,为了口令的安全用户不应选择这种短的数据或有意义的数据作为口令。
(2)数学分析攻击。 所谓数学分析攻击是指密码分析者针对加解密算法的数学基础和某些密码学特性,通过数学求解的方法来破译密码。数学分析攻击是对基于数学难题的各种密码的主要威胁。为了对抗这种数学分析攻击,应当选用具有坚实数学基础和足够复杂的加解密算法。
(3)基于物理的攻击。 侧信道密码分析利用密码系统实现时泄露的额外信息,推导密码系统中的秘密参数。主要方法包括功耗攻击、电磁场攻击和时间攻击等。其中功耗攻击是最常用的手段之一,包括简单功耗分析攻击(SimplePower Analysis attacks,SPA)和差分功耗分析攻击(Differential Power Analysis attacks,DPA),与传统密码分析学相比,这些攻击手段攻击效果显著。有效性远高于基于数学进行密码分析的方法,因此给密码设备带来了严重的威胁。
此外,根据密码分析者可利用的数据资源来分类,可将攻击密码的类型分为以下四种:
(1)仅知密文攻击 (Ciphertext-only attack)。所谓仅知密文攻击是指密码分析者仅根据截获的密文来破译密码。因为密码分析者所能利用的数据资源仅为密文,因此这是对密码分析者最不利的情况。
(2)已知明文攻击 (Known-plaintext attack)。所谓已知明文攻击是指密码分析者根据已经知道的某些明文-密文对来破译密码。例如,密码分析者可能知道从用户终端送到计算机的密文数据从一个标准词“LOGIN”开头。又例如,加密成密文的计算机程序文件特别容易受到这种攻击。这是因为诸如“BEGIN”、“END”、“IF”、“THEN”、“ELSE”等词的密文有规律地在密文中出现,密码分析者可以合理地猜测它们。再例如,加密成密文的数据库文件也特别容易受到这种攻击。这是因为对于特定类型的数据库文件的字段及其取值往往具有规律性,密码分析者可以合理的猜测它们。如学生成绩数据库文件一定会包含诸如姓名、学号、成绩等字段,而且成绩的取值范围在0-100之间。近代密码学认为,一个密码仅当它能经得起已知明文攻击时才是可取的。
(3)选择明文攻击 (Chosen-plaintext attack)。所谓选择明文攻击是指密码分析者能够选择明文并获得相应的密文。这是对密码分析者十分有利的情况。计算机文件系统和数据库系统特别容易受到这种攻击,这是因为用户可以随意选择明文,并获得相应的密文文件和密文数据库。例如,Windows环境下的数据库SuperBase的密码就被作者用选择明文方法破译。如果分析者能够选择明文并获得密文,那么他将会特意选择那些最有可能恢复出密钥的明文。
(4)选择密文攻击 (Chosen-ciphertext attack)。所谓选择密文攻击是指密码分析者能够选择密文并获得相应的明文。这也是对密码分析者十分有利的情况。这种攻击主要攻击公开密钥密码体制,特别是攻击其数字签名。
一个密码,如果无论密码分析者截获了多少密文和用什么技术方法进行攻击都不能被攻破,则称为是 绝对不可破译 的。绝对不可破译的密码在理论上是存在的,这就是著名的“一次一密”密码。但是,由于在密钥管理上的困难,“一次一密”密码是不实用的。理论上,如果能够利用足够的资源,那么任何实际可使用的密码又都是可破译的。
如果一个密码,不能被密码分析者根据可利用的资源所破译,则称为是计算上不可破译的。因为任何秘密都有其时效性,因此,对于我们更有意义的是在 计算上不可破译 (Computationlly unbreakable)的密码。
2.1.3 古典密码
虽然用近代密码学的观点来看,许多古典密码是很不安全的,或者说是极易破译的。但是我们不能忘记古典密码在历史上发挥的巨大作用。另外,编制古典密码的基本方法对于编制近代密码仍然有效,例如置换和代替的方法。
2.1.3.1 古典密码实例
1.置换密码
把明文中的字母重新排列,字母本身不变,但其位置改变了,这样编成的密码称为 置换密码 。
例如把明文按某一顺序排成一个矩阵,其中不足部分用Φ填充,而Φ是明文中不会出现的一个符号。然后按另一顺序选出矩阵中的字母以形成密文,最后截成固定长度的字母组作为密文。
举例:
明文:MING CHEN WU DIAN FA DONG FAN GONG
矩阵:MINGCH 选出顺序:按列
ENWUDI
ANFADO
NGFANG
ONGøøø 其中ø为明文中不会出现的字符,表示空。
密文:MEANO INNGN NWFFG GUAAø CDDNø HIOGø
由此可以看出,改变矩阵的大小和选出顺序可以得到不同形式的密码。置换密码的密钥就是矩阵的大小和选出顺序。置换密码比较简单,但它经不起已知明文攻击。但是,把它与其他密码技术相结合,可以得到十分有效的密码。
2.代替密码
首先构造一个或多个密文字母表,然后用密文字母表中的字母或字母组来代替明文字母或字母组,各字母或字母组的相对位置不变,但其本身改变了。这样编成的密码称为代替密码。按代替所使用的密文字母表的个数可将代替密码分为单表代替密码、多表代替密码和多名代替密码。
单表代替密码又称为简单代替密码。它只使用一个密文字母表,并且用密文字母表中的一个字母来代替一个明文字母表中的一个字母。
设A和B分别为含n个字母的明文字母表和密文字母表:
A={ a 0 ,a 1 ,…,a n-1 }
B={ b 0 ,b 1 ,…,b n-1 }
定义一个由A到B的一一映射:f:A→B
f(a i )=b i
设明文M=(m 0 ,m 1 ,…,m n-1 ),则密文C=(f(m 0 ),f(m 1 ),…,f(m n-1 ))。可见,简单代替密码的密钥就是映射函数f或密文字母表B。
下面介绍几种典型的简单代替密码。
(1)加法密码
加法密码的映射函数为
f(a i )=b i =a j
j=i+k mod n (2-3)
其中,a i ∈A,k是满足0<k<n的正整数。
著名的加法密码是古罗马的凯萨大帝(Caesar)使用过的一种密码。Caesar密码取k=3,因此其密文字母表就是把明文字母表循环右移3位后得到的字母表。例如:
A={A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z}
B={D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z,A,B,C}
明文:MING CHEN WU DIAN FA DONG FAN GONG
密文:PLQJ FKHQ ZX GLDQ ID GRQJ IDQ JRQJ
(2)乘法密码
乘法密码的映射函数为
f(a i )=b i =a j
j=ik mod n (2-4)
其中,要求k与n互素。这是因为仅当(k,n)=1时,才存在两个整数x,y使得xk+yn=1,才有xk=1 mod n,才有i=xj mod n,密码才能正确解密。
例如,当用英文字母表作为明文字母表而取k=13时,因为(13,26)=13≠1,便会出现:
f(A)=f(C)=f(E)=f(G)=f(I)=f(K)=f(M)=f(O)=f(Q)=f(S)=f(U)=f(W)=f(Y)=A
f(B)=f(D)=f(F)=f(H)=f(J)=f(L)=f(N)=f(P)=f(R)=f(T)=f(V)=f(X)=f(Z)=N
此时的密文字母表变为
B={A,N,A,N,A,N,A,N,A,N,A,N,A,N,A,N,A,N,A,N,A,N,A,N,A,N}
整个密文字母表只包含A和N两个字母,密文将不能正确解密。
而若选k=5,因为(5,26)=1,便得到如下的合理的密文字母表:
A={A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z}
B={A,F,K,P,U,Z,E,J,O,T,Y,D,I,N,S,X.C,H,M,R,W,B,G,L,Q,V}
(3)仿射密码
乘法密码和加法密码相结合便构成仿射密码。仿射密码的映射函数为
f(a i )=b i =a j
j=ik 1 +k 0 mod n (2-5)
其中,要求(k 1 ,n)=1,0≤k 0 <n,且不允许同时有k 1 =1 k 0 =0。
简单代替密码很容易被破译,其原因在于只使用一个密文字母表,从而使得明文中的每一个字母都只用唯一的一个密文字母表来代替。提高代替密码强度的一种方法是采用多个密文字母表,使明文中的每一个字母都有多种可能的字母来代替。
构造d个密文字母表:
B j ={b j0 , b j1 ,…,b jn-1 ) j=0,1,…,d-1
定义d个映射
f j :A→B j
f j (a i )=b j1 j=ik mod n (2-6)
设密文M=(m 0 ,m 1 ,…,m d-1 ,m d ,…),C=(f 0 (m 0 ),f 1 (m 1 ),…,f d-1 (m d-1 ),f 0 (m d )…)。
由于加密用到多个密文字母表,故称为多表代替密码。多表代替密码的密钥就是这组映射函数或密文字母表。
最著名的多表代替密码要算16世纪法国密码学者Vigenre使用过的 Vigenre密码 。
Vigenre密码使用26个密文字母表,像加法密码一样,它们是依此把明文字母表循环右移0,1,2,…,25位的结果。选用一个词组或短语作密钥,以密钥字母控制使用哪一个密文字母表。把26个密文字母表排在一起称为Vigenre方阵,如表2-1所示。
表2-1 Vigenre方阵

Vigenre密码的代替规则是用明文字母在Vigenre方阵中的列和密钥字母在Vigenre方阵中的行的交点处的字母来代替该明文字母。例如,设明文字母为P,密钥字母为Y,则用字母N来代替明文字母P。又例如:
明文: MING CHEN WU DIAN FA DONG FAN GONG
密钥: XING CHUI PING YE KUO YUE YONG DA JIANG LIU
密文: JQAME OYVLC QOYRP URMHK DOAMR NP
Vigenre密码的解密就是利用Vigenre方阵进行反代替。
3.代数密码
美国电话电报公司的Gillbert Vernam在1917年为电报通信设计了一种非常方便的密码,后来被称为 Vernam密码 。Vernam密码奠定了序列密码的基础,在近代计算机和通信系统中得到广泛应用。
Vernam密码的明文、密钥和密文均用二元数字序列表示。
设明文M=(m 0 ,m 1 ,…,m n-1 ),密钥K=(k 0 ,k 1 ,…,k n-1 ),密文C=(c 0 ,c 1 ,…,c n-1 ),其中m i ,k i ,c i ∈GF(2),则
c i =m i ⊕k i i=0,1,…,n-1 (2-7)
这说明要编制Vernam密码,只需要把明文和密钥表示成二元序列,再把它们按位模2相加便可。根据式(2-7),有
m i =c i ⊕k i (2-8)
式(2-8)说明要解密Vernam密码,只需要把密文和密钥的二元序列对位模2相加便可。可见,Vernam密码的加密和解密非常简单,而且特别适合计算机和通信系统的应用。
例如:
明文: DATA
1000100 1000001 1010100 1000001
密钥: LAMB
1001100 1000001 1001101 1000010
密文: 0001000 0000000 0011001 0000011
Vernam密码属于序列密码。它的一个突出优点是其加密运算与解密运算相同,都是模2加运算。这使得无论是硬件实现还是软件实现这都是最简单的,而且加解密可共用同一个软件模块或硬件电路,使工程设计制作的工作量减少一半。
在数学上,如果一个变换的正变换和逆变换相同,f=f –1 ,则称其为 对合运算 。例如,模2加运算⊕就是一种对合运算。因此,在密码设计中都希望将其加密算法设计成对合运算,这样使加解密共用同一算法,工程实现工作量减少一半。例如,著名的DES和IDEA等密码的加密运算都是对合运算。
Vernam密码经不起已知明文攻击。这是因为
k i =c i ⊕m i (2-9)
只要知道了某些明文-密文对,便可以迅速确定出相应的密钥。如果同一密钥重复使用或密钥本身包含重复,则Vernam密码将是不安全的。据此,为了增强Vernam密码的强度,应当避免密钥重复使用,避免密钥本身包含重复。一种极端情况是:
①密钥是真正的随机序列;
②密钥至少和明文一样长;
③一个密钥只使用一次。
如果能够做到这些,则密码就是绝对不可破译的了。这便是著名的 “一次一密”密码 (one time pad)。然而“一次一密”密码在实际上是行不通的。首先,“一次一密”密码要求密钥是真正的随机序列,这在实际上是不可能完全做到的。其次,“一次一密”密码要求密钥至少和明文一样长而且一个密钥只使用一次。这意味着必须经常地产生、存储大量的、很长的密钥,并且能够通过安全的途径将每次使用的密钥告诉收信者。这在实际上也是极困难的。可见,“一次一密”密码在实际的密钥管理和密钥分配方面是非常困难的,因而是行不通的。
虽然“一次一密”密码在实际上是行不通的,但它在理论上的成功却给我们展示出一个令人向往的目标。密码学者认为,如果能够用某种实际方法来模仿“一次一密”密码,将会得到一种安全性极好的实用密码。无疑这是设计密码的一种有效途径。
2.1.3.2 古典密码破译方法
1.穷举分析
对于加法密码,根据式(2-3)可知,密钥整数k只有n-1个不同的取值。对于明文字母表为英文字母表的情况,k只有25种可能的取值。即使是对于明文字母表为8位扩展ASCII码而言,k也只有255种可能的取值。因此,只要对k的可能取值逐一穷举就可破译加法密码。
乘法密码比加法密码更容易破译。根据式(2-4)可知,密钥整数k要满足条件(n,k)=1,因此,k只有φ(n)个不同的取值。去掉k=1这一恒等情况,k的取值只有φ(n)-1种。这里φ(n)为n的欧拉函数。对于明文字母表为英文字母表的情况,k只能取3,5,7,9,11,15,17,19,21,23,25共11种不同的取值,比加法密码弱得多。
仿射密码的保密性能好些。但根据式(2-5),可能的密钥也只有nφ(n)-1种。对于明文字母表为英文字母表的情况,可能的密钥只有26×12-1=311种。这一数目对于古代密码分析者企图用穷举全部密钥的方法破译密码,可能会造成一定的困难,然而对于应用计算机进行破译来说,这就是微不足道的了。
2.统计分析
任何自然语言都有许多固有的统计特性。如果自然语言的这种统计特性在密文中有所反映,则密码分析者便可以通过分析明文和密文的统计规律而将密码破译。许多古典密码都可以用统计分析的方法破译。
随便阅读一篇英文文献,立刻就会发现,其中字母E出现的次数比其他字母都多。如果进行认真统计,并且所统计的文献的篇幅足够长,便可以发现各字母出现的相对频率十分稳定。而且,只要文献不特别专门化,对不同的文献进行统计所得的频率分布大体相同。根据各字母频率的大小可将英文字母分为几组。表2-2描述了这一分组情况。
表2-2 英文字母频率分布

不仅单字母以相当稳当的频率出现,而且双字母组(相邻的两个字母)和三字母组(相邻的三个字母)同样如此。出现频率最高的30个双字母组依此是:
TH HE IN ER AN RE ED ON
ES ST EN AT TO NT HA ND
OU EA NG AS OR TI IS ET
ITAR TE SE HI OF
出现频率最高的20个三字母组依此是:
THE ING AND HER ERE ENT THA NTH WAS
ETH FOR DTH HAT SHE IONHIS STHERS
VER
特别值得注意的是,THE的频率几乎是排在第二位的ING的3倍,这对于破译密码是很有帮助的。此外,统计资料还表明:
①英文单词以E、S、D、T为结尾的超过一半。
②英文单词以T、A、S、W为起始字母的约占一半。
以上所有这些统计数据,对于密码分析者来说都是十分有用的信息。
破译单代替密码的大致过程是:首先统计密文的各种统计特征,如果密文量比较多,则完成这步后便可确定出大部分密文字母;其次分析双字母、三字母密文组,以区分元音和辅音字母;最后分析字母较多的密文,在这一过程中大胆使用猜测的方法,如果猜对一个或几个词,就会大大加快破译过程。
密码破译是十分复杂和需要极高智力的劳动。世界上第一台计算机一诞生便投入密码破译的应用,目前计算机已经成为密码破译的主要工具。可以预计,随着计算机科学技术的发展,计算机在密码破译中将会发挥更大的作用。


