
囚徒困境模型
囚徒困境模型是用一个小故事来表达的。
 故事模型
故事模型
两个人因盗窃被捕,警方怀疑其有抢劫行为但未获得确凿证据可以判他们犯了抢劫罪,除非有一个人供认或两个人都供认。即使两个人都不供认,也可判他们犯盗窃物品的轻罪。
囚徒被分离审查,不允许他们之间互通消息,并交代政策如下:如果两个人都供认,每个人都将因抢劫罪加盗窃罪被判三年监禁;如果两个人都拒供,则两个人都将因盗窃罪被判处半年监禁;如果一个人供认而另一个拒供,则供认者被认为有立功表现而免受处罚,拒供者将因抢劫罪、盗窃罪以及抗拒从严而被重判5年。
我们用赢利表(payoff table)将两名囚徒面临的博弈问题表示如下(见图3-1):
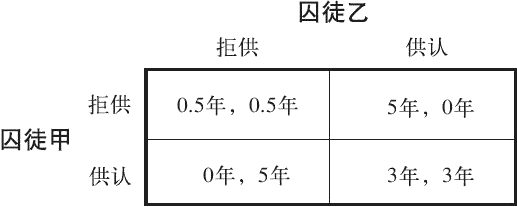
图3-1 囚徒的困境
赢利表是两个局中人且策略离散情形常用的一种表达博弈的工具。其解读方式是这样的:最左边是局中人1(本例中为囚徒甲),最上边是局中人2(本例中为囚徒乙);左边的“拒供”“供认”是局中人1的策略,上边的“拒供”“供认”是局中人2的策略;四个单元格是双方策略的组合情况(本例中每人有2个策略,策略组合就为2×2=4(种)),每个单元格即一种策略组合;每个单元格中有两个数字,第一个数字代表局中人1(左边那个人)的赢利,第二个数字代表局中人2(上边那个人)的赢利。
从图3-1赢利表中可发现,如果两个囚徒都拒供,则每个人判0.5年;如果两个囚徒都供认,则每个人判3年。相比之下,两个囚徒都拒供是对大家来说最好的结果,都供认则是最糟糕的结果。
但是,这个对大家最好的结果实际上不大容易发生。因为每个囚徒都会发现:
·如果对方拒供,则自己供认便可立即获得释放,而自己拒供则会被判0.5年,因此供认是较好的选择;
·如果对方供认,则自己供认将被判3年,而自己拒供则会被判5年,因此供认是较好的选择;
·因此无论对方拒供或供认,自己选择供认始终是更好的。
由于每个囚徒都发现供认是自己更好的选择,于是,博弈的稳定结果是两个囚徒都会选择供认。我们把这种稳定结果称为博弈的纳什均衡。

这样的结果多少有点令人意外。他们为什么不可以订立一个攻守同盟,都选择“拒供”从而获得一个对大家都更有利的结果呢?若两个人在被捕前曾在关二爷面前发誓绝不招供,那么他们能不能达成合作,选择拒供呢?即使如此,同盟可能还是难以结成的,原因很简单,一旦两个人被捕面临隔离审查,每个人会担心对方背弃盟约。如果囚徒甲是坚守盟约的人,那么囚徒乙正好可以在事前诱使他订立盟约,然后被捕后囚徒乙就可以通过背盟而逍遥法外;囚徒甲当然也很清楚做一个坚守盟约的人很可能被囚徒乙利用,所以他为什么要坚持盟约呢?反过来,如果乙是坚守盟约者,推理也一样。结果是,两个囚徒之间不可能达成稳定的盟约。
囚徒困境通常被看作个人理性冲突和集体理性冲突的经典情形。因为在囚徒困境局势中,每个人根据自己的利益做出决策,但是最后的结果却是集体遭殃。现实中诸多的问题和现象,正是囚徒困境问题的翻版。


