我国魏晋时期杰出的数学家刘徽（约225—295年，中国古代数学家）在263年创立了“割圆术”，解决了当时的数学难题——求圆的周长。他是借助圆内接正多边形的周长，得出圆的周长。具体作法是：作圆的内接正六边形；再平分每条边对应的弧，作圆的内接正十二边形；用同样的方法继续作圆的内接正二十四边形、正四十八边形……如图2-1所示。

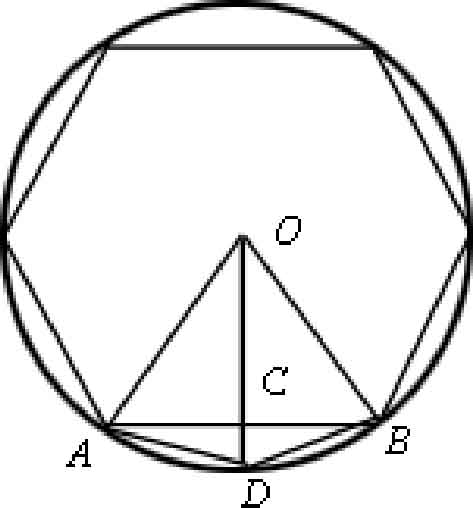
图2-1

设圆的半径为 r ，圆内接正 n 边形边长为 l n ，周长为 L n 。将边数加倍后，得到圆内接正2 n 边形，其边长、周长分别为 l 2 n ， L 2 n 。若 l n 已知，可由勾股定理求出 l 2 n ，由图2-1可得

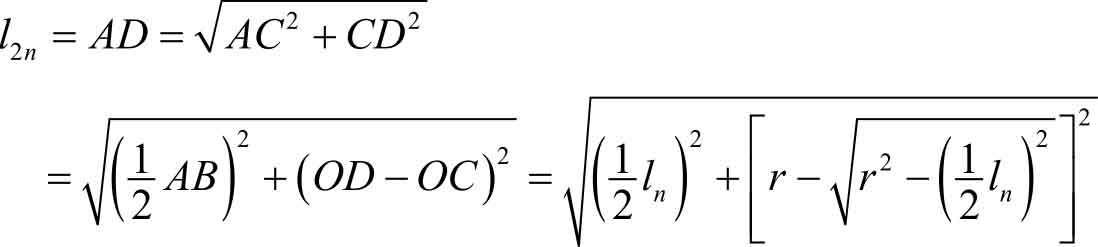
随着圆内接正多边形边数的无限增加，圆内接正多边形的周长与圆的周长的差别无限减少，当边的数量相当大所对应边长相当小，以至于小到不能再小时，多边形的周长就无限地接近于圆的周长。用刘徽叙述这种做法时的话来说：“割之弥细，所失弥少。割之又割，以至不可割，则与圆周合体而无所失矣。”这种“割圆术”所运用的数学思想，正是我们要学习的极限思想，即用无限逼近的方式来研究数量的变化趋势的思想。

在数学中，极限的概念和思想非常重要。研究变量在无限变化中的变化趋势，从有限中认识无限，从近似中认识精确，从量变中认识质变，都要用到极限。在本章中我们将学习数列的极限和函数的极限等概念及有关运算法则，并利用极限讨论函数的连续性。