2.3 极限的运算
利用极限的定义只能计算一些很简单的函数的极限，而极限的求法是本章的基本运算，应熟练掌握。
2.3.1 极限的四则运算法则
定理2.5 设 x 是在同一变化过程中，且lim u （ x ）= A ，lim v （ x ）= B ，则
(1) lim[ u ( x )± v ( x )]=lim u ( x )±lim v ( x )= A ± B ;
(2) lim[ u ( x )· v ( x )]=lim u ( x )·lim v ( x )= AB ;
(3
lim
v
(
x
)=
B
≠0).
证 在此我们只证（2），其他证法类同。
因为lim u （ x ）= A ，lim v （ x ）= B ，由定理2.3可知
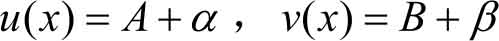
其中 α ， β 是同一变化过程中的无穷小量，于是
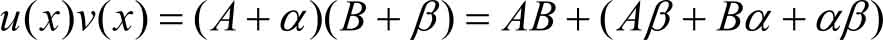
由无穷小的性质可知 Aβ + Bα + αβ 仍是无穷小，再由定理2.3（极限与无穷小的关系）得lim u （ x ）· v （ x ）=lim[ AB +（ Aβ + Bα + αβ ）]= AB =lim u （ x ）·lim v （ x ）
证毕。
上述极限的四则运算法则，可以推广到有限多个函数的代数和及乘法的情况，但在使用法则时，应注意以下几点。
（1） 极限的四则运算法则只有在参与运算函数的极限各自存在条件下才能使用。
（2） 在使用除法法则时，分母的极限不能为零。
推论 设lim u （ x ）存在， C 为常数， n 为正整数，则有
(1) lim[ Cu ( x )]= C lim u ( x );
(2) lim[ u ( x )] n =[lim u ( x )] n .
例2.10
求
。
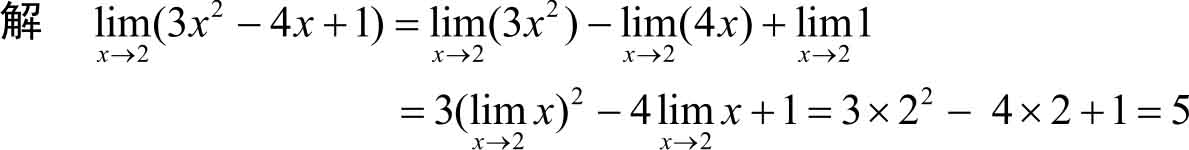
例2.11
求
。
例2.12
求
。
解
因为
=1
2
-3+2=0，所以此题不能直接使用运算法则。在分母为零的情况下，求极限的方法将取决于分子极限的情况，由于
=2×1-3=-1≠0，因此我们先求原函数倒数的极限，即
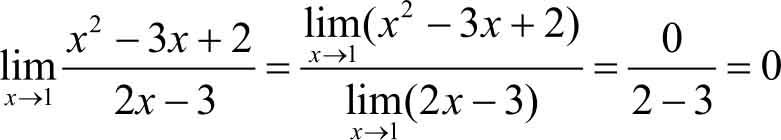
即
是
x
→1时的无穷小，由无穷小与无穷大的倒数关系可知：
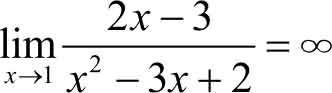
例2.13
求
。
解
当
x
=1时，分子、分母都为0，呈现
形式。而在考虑
x
→1时的极限时，考虑的是
x
越来越靠近1，不用关心“1”时情况。当
x
≠1时，可约去公因式（
x
-1）再用运算法则。即
综上讨论，有理函数在 x → x 0 时的极限是容易求得的，下面对 x →∞时极限求法举例。
例2.14
求
。
解
当
x
→∞时，分子、分母的极限都不存在（呈现
形式），所以不能运用极限的四则运算法则。我们把分子、分母同时除以它们的最高次幂
x
2
，然后再求极限。
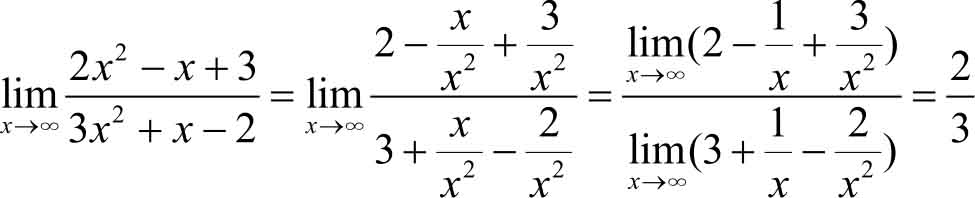
一般地，当 x →∞时，有理分式（ a 0 ≠0， b 0 ≠0）的极限有以下结果：
例2.15 求下列函数的极限。
解
（1）因为当
x
→∞时，此极限呈现
形式，且分母的最高次幂大于分子的最高次幂，即
m
＞
n
，所以由式（2.1）得
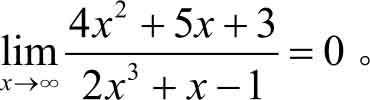
（2） 我们观察分子、分母的最高次幂可以发现，分子乘积的结果为三次多项式，与分母的最高次幂相同，即 m = n ，所以由式（2.1）可知，极限值应为分子、分母最高次项 x 3 系数之比，即
例2.16 求下列函数的极限。
解 （1） 当 x →1时，上式两项极限均不存在，（呈现∞-∞形式），我们先通分，化成一个分式，再求极限：
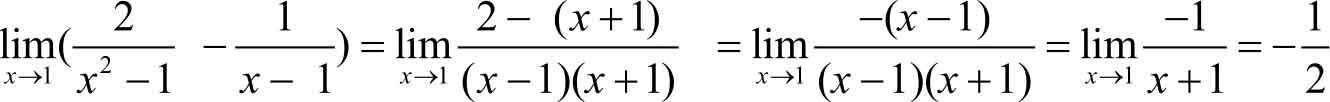
（2）
解法一
当
x
→0时，分子、分母极限均为0（呈现
形式），不能用极限四则运算中的除法法则。这时，可先对分子有理化，然后求极限：
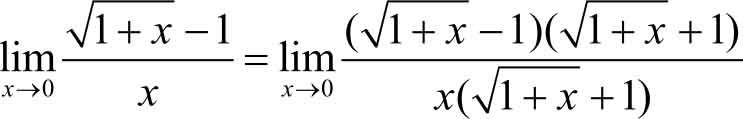
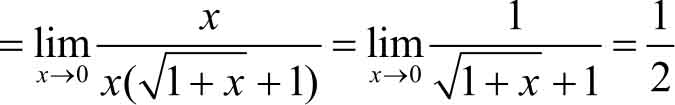
解法二
当
x
→0时，由无穷小等价代换可知
，所以
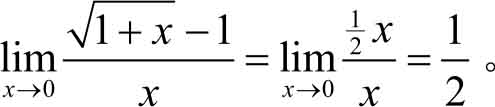
（3） 因为当
x
→+∞时，
x
sin
x
的极限不存在，不能使用极限四则运算法则，但我们注意到
≤1，即sin
x
有界，又
根据有界量与无穷小乘积仍是无穷小的性质，得
（4） 对于数列极限的求法与函数极限的求法类似，只需用前 n 项和公式先做形式上的转换即可。
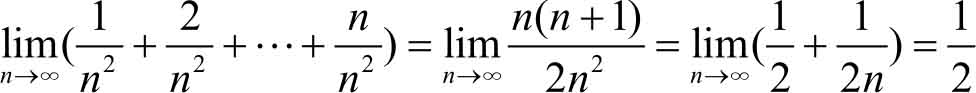
此题必须注意，当
n
→∞时，
均为无穷小，但它不是有限个无穷小的代数和，而是无限个无穷小的代数和，故不能直接使用无穷小的性质。通过上例我们也可以看到，无限个无穷小的代数和未必是无穷小。
小结：
综上讨论，如果所求极限呈现
，∞-∞等形式不能直接用极限法则时，必须先对原式进行恒等变形（约分、通分、有理化、变量代换等），然后再求极限。对于满足无穷小性质，等价无穷小代替的也可以使用它们进行求极限。
2.3.2 两个重要极限
1.
证
因为
，即
x
改变符号时，
的值不变，所以只讨论
x
由正向趋于零的情形即可。
作单位圆，如图2-10所示，取∠ AOB = x （rad），过 A 点作圆的切线交 OB 延长线于 D ，过 B 作垂线交 OA 于点 C ，于是有 BC =sin x ， AB = x ， AD =tan x 。
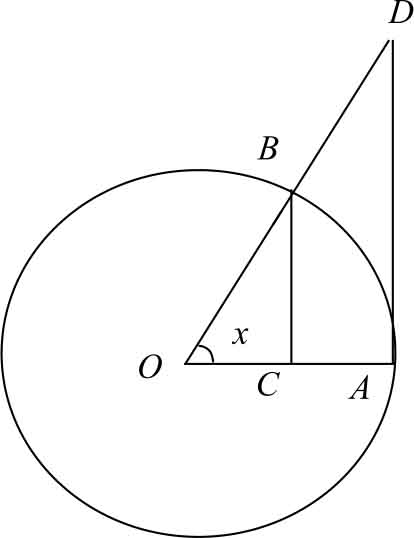
图2-10
因为
，由极限的夹逼准则可知：
证毕。
例2.17
求
。
解 设 t =3 x ，当 x →0时， t =3 x →0，则
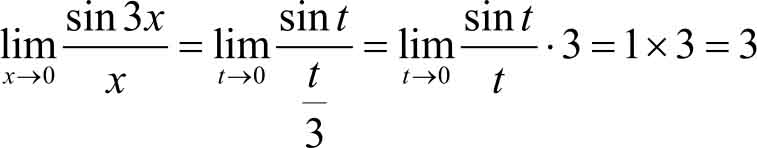
由此可见，我们可以把式（2.2）形象地写成
（三角形“Δ”代表同一无穷小量的代数式）。特别注意，这个重要极限是
形式的。
如果Δ取
，那么就有
。也就是说：
例2.18
求
。
例2.19
求
。
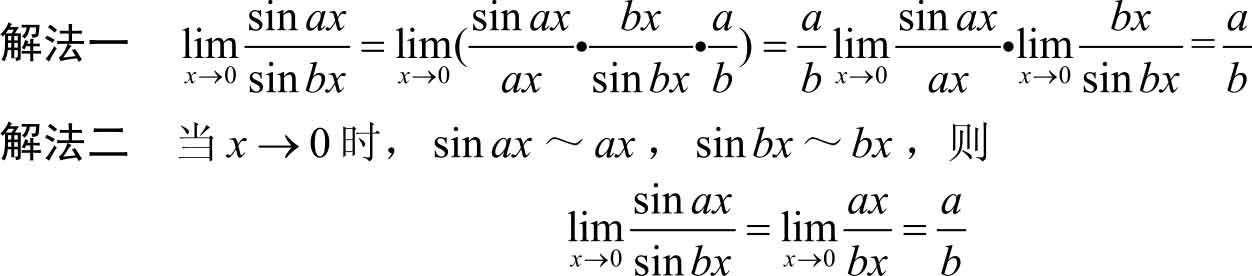
例2.20
求
。
例2.21
求
。
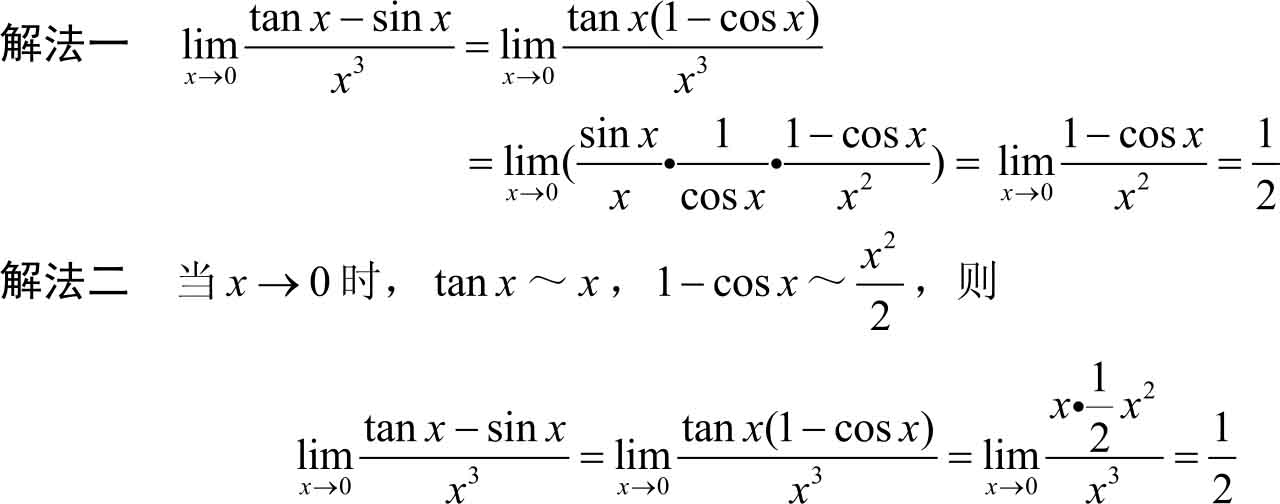
这里需要注意的是，无穷小的等价代换是对分子或分母的整体代换（或对分子、分母的因式代换），而对分子或分母中“+”，“-”号连接的各部分不能分别作代替。例如上例中，若tan x ～ x ，sin x ～ x 进行代替后，则有
这样就错了！
2.
首先，我们利用计算器算出
的一些函数值，列在表2-1中。观察当
x
→∞时，函数
的变化趋势。
表2-1
从表 2-1 中可以看到，当
x
→∞时，
趋于一个定数，这个数是无理数 e。e=2.718 281 72…，即
。
类似于式（2.3），为了强调其形式，我们把它形象地写成
（三角“Δ”代表同一无穷大量）。特别注意，这个重要极限是1 ∞ 形式的。
如果Δ取
，那么就有
。也就是说：
观察式（2.5）和式（2.6）可知，当底的变量项与指数是互为倒数的1 ∞ 形式时，极限即为e。
例2.22
求
。
解 所求极限类型是1 ∞ 形式的，所以
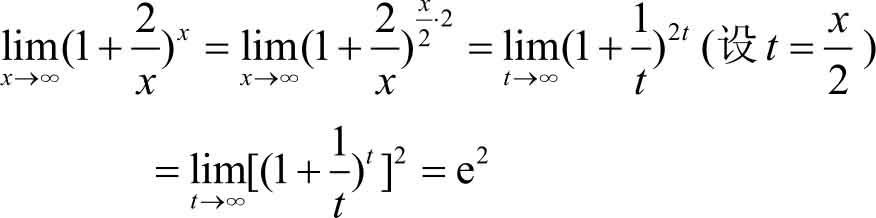
例2.23
求
。
解 所求极限类型是1 ∞ 形式的，所以
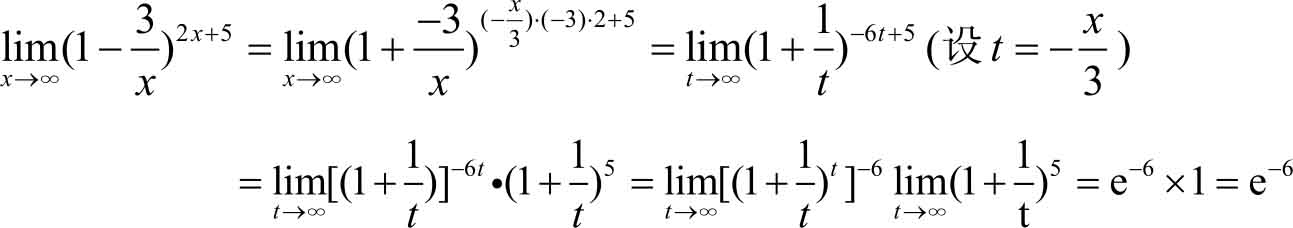
请思考：
将例2.22、例2.23一般化，例2.22中的2与例2.23的-3用
a
代换，例2.23中的2用
b
代换，5用
C
代换，关于极限
，你能给出结果吗？结果是什么？
一般地，可以有下面结论：
当作
代换时，可得
，即
例2.24
求
。
解
因为
，式中
，b=3，c=-2，所以
例2.25
求
（
a
为常数）。
解
所求极限类型是1
∞
形式的，令
，则
x
=2
at
+
a
，可得
例2.26
求
。
解 所求极限类型是1 ∞ 形式的，根据式（2.8）可知， a = -k ，b=1，c=2，所以
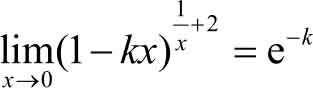
作为第二个重要极限的应用，我们介绍复利计息公式。所谓复利计息，就是将第一期利息和本金之和作为第二期的本金，然后反复计息。
设本金为 p ，年利率为 r ，一年后的本利和为 s 1 ，则
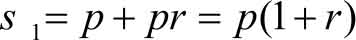
把 s 1 作为本金存入，第二年末的本利和为 s 2 ，则
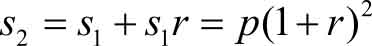
再把 s 2 存入，如此反复，第 n 年末的本利和为 s n ，则
这是以年为期的复利计息公式。
若把一年分为 12 期，按月进行计息，此时每期利率可以认为是
，于是推出
n
年的本利和为
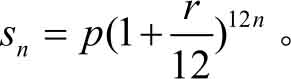
若把一年分成
t
期计息，此时每期利率可以认为是
，于是推出
n
年的本利和为
假如计息期无限缩短，即期数 t →∞时，于是得到复利公式为
这是连续复利计息公式。
例2.27 现有本金10 000元，年利率为3.3%，存款期2年。求：（1）以年为期的到期的本利和；（2）以连续复利计息到期的本利和。
解 （1） p =10 000， r =3.3%， n =2，由公式（2.9）可知二年的本利和为
（2） p =10 000， r =3.3%， n =2，由公式（2.10）可知二年的本利和为
s 2 = p ·e r . n =10 000·e 0.033×2 ≈10 682.23 （元）。
习题2.3
1.求下列极限：
2.求下列极限。
3.求下列极限。
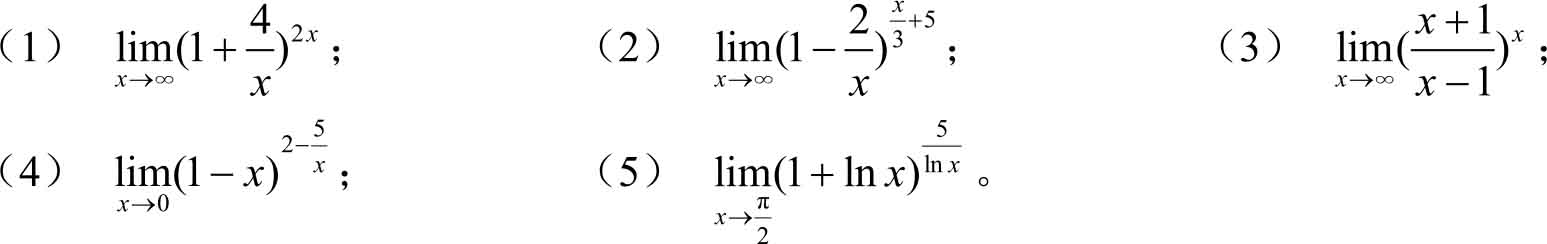
4.某人从商业银行贷款150 000元用于购买一部轿车，贷款年利率为5.6%，贷款期5年，到期一次性还款，以连续复利计息到期需要还款多少？
