3.4 微分及其应用
本节介绍微分学的另一个基本概念——微分。
实际中有时需要考虑在自变量有微小变化时函数的改变量的计算问题。通常函数改变量的计算比较复杂。因此需要建立函数改变量近似值的计算方法,使其既便于计算又有一定的精确度,这就是本节要讨论的问题。
3.4.1 两个实例
1.面积改变量的近似值
设正方形的面积为 A ,当边长由 x 变到 x +Δ x 时,面积 A 有相应的改变量Δ A (如图3-5所示),则
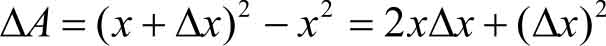
Δ A 由两部分组成。第一部分2 x Δ x 是Δ x 的线性函数,当Δ x →0时,它是Δ x 的同阶无穷小;而第二部分(Δ x ) 2 是比Δ x 高阶的无穷小,因此,当 Δ x 很小时,(Δ x ) 2 可以忽略不计,这时
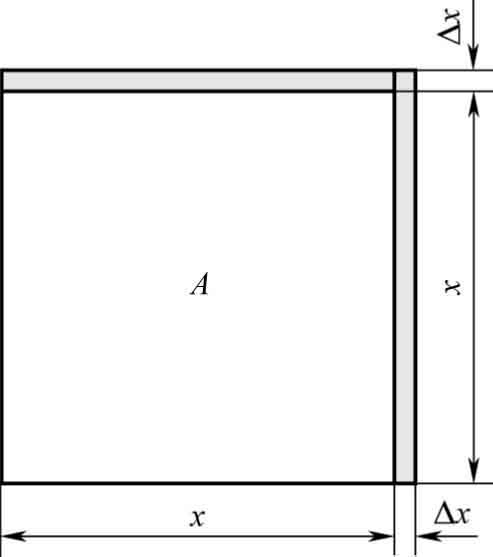
图3-5
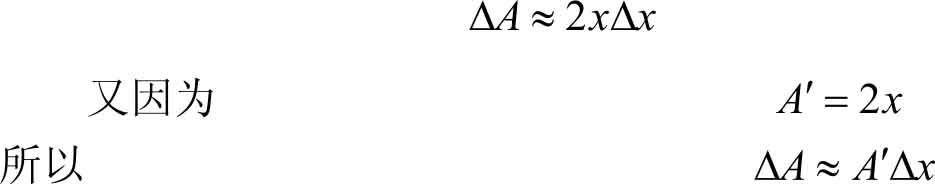
2.路程改变量的近似值
自由落体的路程
s
与时间
t
的关系是
 。当时间从
t
变到
t
+Δ
t
时,路程
s
有相应的改变量Δ
s
,则
。当时间从
t
变到
t
+Δ
t
时,路程
s
有相应的改变量Δ
s
,则
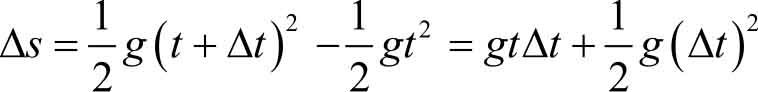
Δ
s
由两部分组成。第一部分
gt
Δ
t
是Δ
t
的线性函数,当Δ
t
→0时,它是Δ
t
的同阶无穷小;而第二部分
 是比Δ
t
高阶的无穷小,因此,当
是比Δ
t
高阶的无穷小,因此,当
 很小时,
很小时,
 可以忽略不计,这时
可以忽略不计,这时

上面两例虽然具体意义不同,但它们有一个明显的共同点,即函数改变量的近似值可表示为函数的导数与自变量改变量的乘积,而产生的误差是一个比自变量改变量高阶的无穷小。
上述结论对于一般的函数是否成立呢?下面说明对于可导函数都有此结论。
设函数 y = f ( x )在点 x 处可导,即
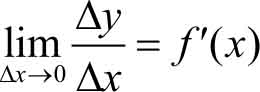
根据极限与无穷小的关系有

因为 α 是当Δ x →0时的无穷小量,所以 α Δ x = o (Δ x ),从而
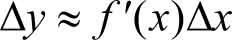
函数 y = f ( x )改变量的近似值 f ′( x )Δ x 称为函数的微分。
3.4.2 微分的概念
1.微分的定义
定义3.2 如果函数 y = f ( x )在 x 处具有导数 f′ ( x ),则称 f′ ( x )Δ x 为函数 y = f ( x )在 x 处的 微分 ,记作dy或d f ( x ),即d y = f ′( x )Δ x ,此时称函数 f ( x )在 x 处可微。
特别地,对于函数 y = x ,有
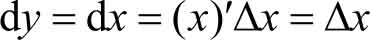
即d x =Δ x 。因此,自变量的微分就是它的改变量。于是得

进一步可得
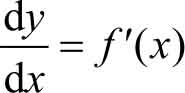
由此可以看出,函数的导数等于函数的微分与自变量的微分之商,因此也称导数为微商。求导数与求微分的运算统称为微分法。
应当注意,微分与导数虽然有着密切的联系,但它们是有区别的:导数是函数在一点处的变化率,导数的值只与 x 有关;而微分是函数在一点处由自变量改变量所引起的函数改变量的近似值,微分的值与 x 和Δ x 都有关。
2.微分的几何意义
设函数 y = f ( x )的图像如图3-6所示, M ( x , y )为曲线上的定点,过点 M 作曲线的切线 MT ,其傾角为 α ,当自变量在点 x 处取得改变量Δ x 时,就得到曲线上的另一点 M 1 ( x +Δ x , y +Δ y ),从图3-6可知
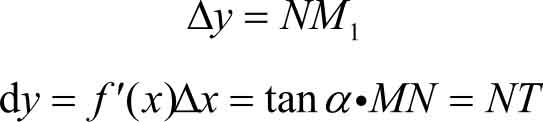
由此可见,函数 y = f ( x )的微分的几何意义就是曲线 y = f ( x )在 M 点处切线之纵坐标的改变量。
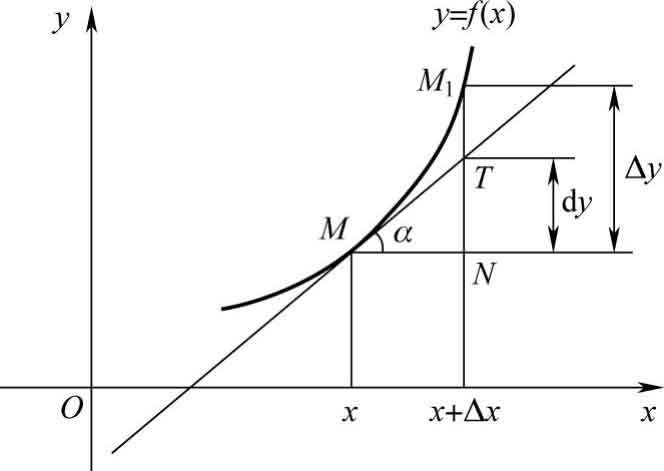
图3-6
3.4.3 微分公式
因为d y = f′ ( x )d x ,所以计算微分便归结为计算导数。由导数的基本公式和运算法则,容易推出微分的基本公式和运算法则,见表3-2和表3-3所列。
表3-2

表3-3

其中, u = u ( x ), v = v ( x ), C 为常数。
例3.33 求函数 y = x 2 当 x =1,Δ x =0.1时的微分。

例3.34
求函数
 的微分。
的微分。

3.4.4 复合函数的微分
把复合函数 y = f [ φ ( x )]分解为 y = f ( u ), u = φ ( x )。则
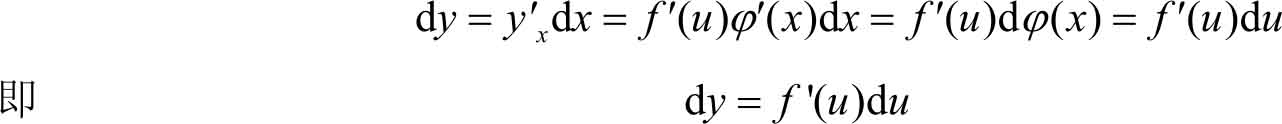
这就是说,无论 u 是自变量还是中间变量, y = f ( u )的微分d y 总可以写成d y = f ′( u )d u 的形式。这一性质称为微分形式不变性。有时,利用这一性质求复合函数的微分比较方便。
例3.35 求函数 y =ln sin x 的微分。
解 设 u =sin x ,则
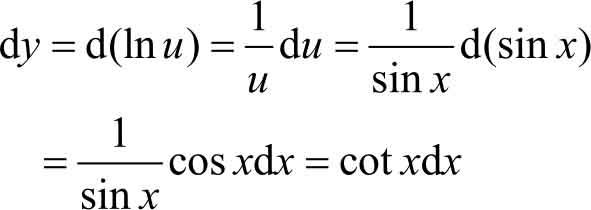
例3.36
求函数
y
=
 的微分。
的微分。
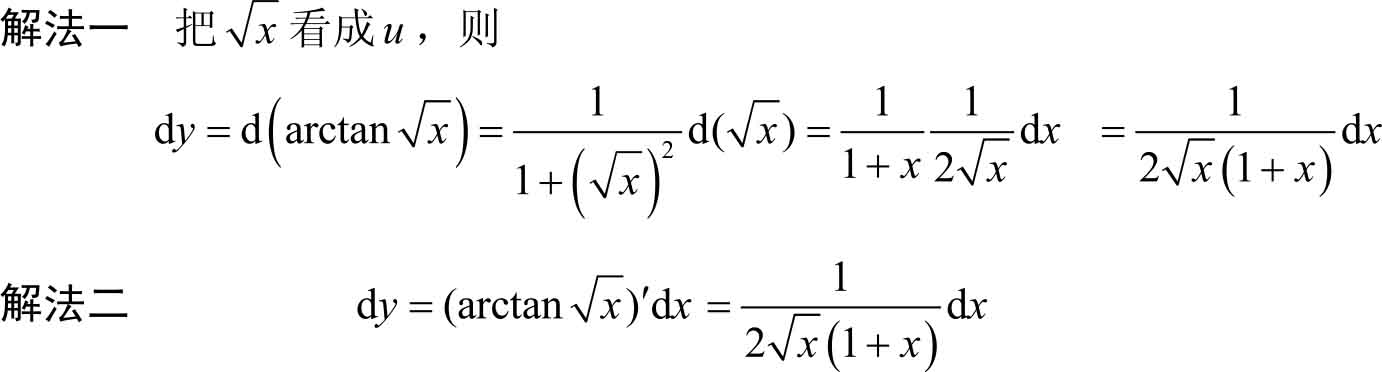
3.4.5 微分的应用
由微分的定义可知,当函数
y
=
f
(
x
)在点
x
0
处的导数
f
′(
x
0
)≠0,且
 很小时有
很小时有
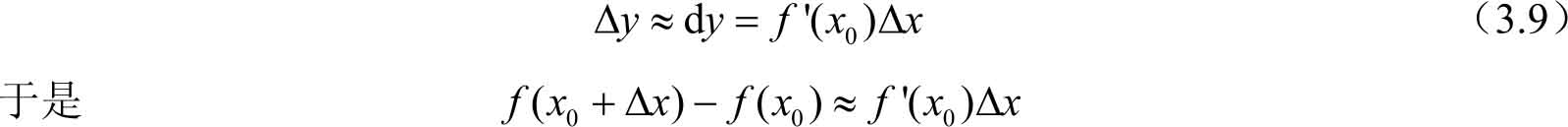
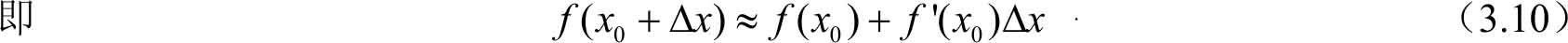
式(3.9)可以用来求函数改变量的近似值,式(3.10)可以用来计算函数的近似值。
例3.37 有一批半径为1 cm 的球,为了提高球表面的光洁度,要镀上一层厚度为0.01 cm的铜,已知铜的密度为8.9 g/cm 3 ,试估计一下每个球需用多少克铜?
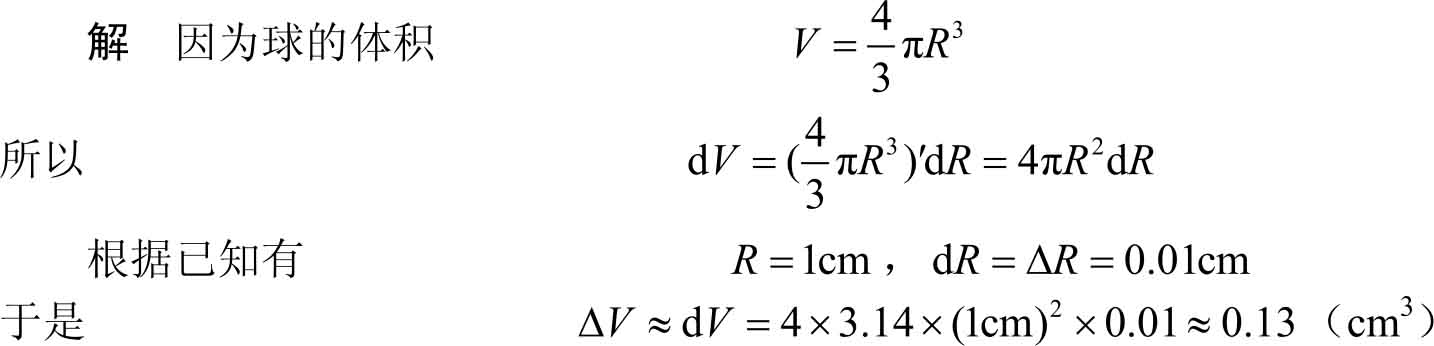
因此,镀每个球大约需用铜0.13×8.9=1.16g。
求函数的近似值,应先找到合适的函数 f ( x ),再选取 x 0 ,Δ x ,然后带入式(3.10)。
例3.38
求
 的近似值。
的近似值。
解
设
f
(
x
)=
 ,由式(3.10)有
,由式(3.10)有
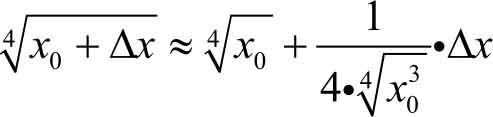
取 x 0 =1,Δ x =0.02,有
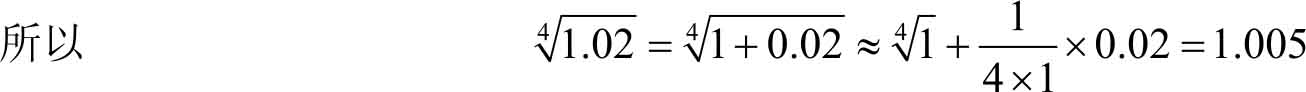
例3.39 求arcsin 0.4983的近似值。
解 设 f ( x )=arcsin x ,由式(3.10)有

取 x 0 =0.5,Δ x =-0.0017,可得
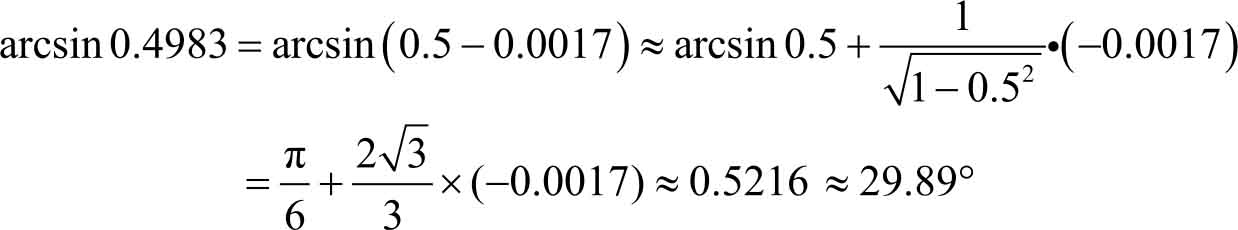
习题3.4
1.设 x 的值从 x =1变到 x =1.01,试求函数 y =2 x 2 -x 的改变量和微分。
2.求下列函数的微分。
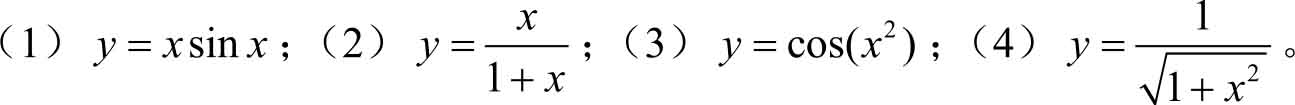
3.利用微分的近似计算公式,求下列各式的近似值。
(1
 2) cos 29°;(3) arctan 1.003.
2) cos 29°;(3) arctan 1.003.
4.一金属圆管,它的内半径为10cm,当管壁厚为0.05 cm时,利用微分来计算这个圆管截面面积的近似值。


