3.5 导数在经济学中的应用
前面我们从实际问题中抽象出了导数的概念,并利用导数的定义求一些函数的导数,现在我们从抽象的概念再回到具体的问题中去。下面介绍变化率和相对变化率。
1.变化率
在实际问题中常把导数称为变化率,因为,对于函数 y = f ( x )来说,用
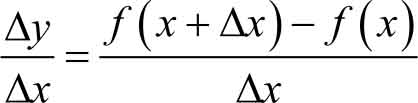
表示自变量
x
每改变一个单位时,函数
y
的平均变化量,所以
 称为函数
y
=
f
(
x
)的平均变化率。
称为函数
y
=
f
(
x
)的平均变化率。
当Δ
x
→0时,若
y
可导,则
 称为函数
y
=
f
(
x
)的变化率。
称为函数
y
=
f
(
x
)的变化率。
2.边际分析
边际概念是经济学中的重要概念,通常指经济函数的变化率。利用导数研究经济变量的边际变化的方法,称为 边际分析方法 。
(1) 边际成本
在经济学中, 边际成本 定义为产量增加一个单位时总成本的增量,即总成本对产量的变化率。
设某产品产量为 q 单位时所需的总成本函数为 C = C ( q ) [ C ( q )可导],则产量增加一个单位时总成本的增量Δ C ( q )为
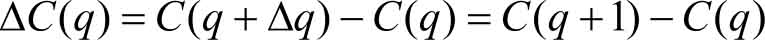
又由于产量增加一个单位与总产量相比很小,即
 很小(Δ
q
=1)。由微分近似计算可知:
很小(Δ
q
=1)。由微分近似计算可知:
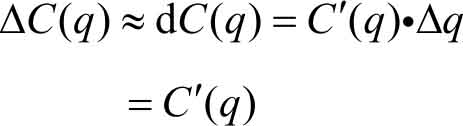
所以 边际成本就是总成本关于产量 q 的导数 。
(2) 边际收入
在经济学中, 边际收入 定义为多销售一个单位产品时总收入的增量,即总收入关于产品销售量 q 的变化率。
设某产品销售量为 q 单位时的总收入函数为 R = R ( q ) [ R ( q )可导],则
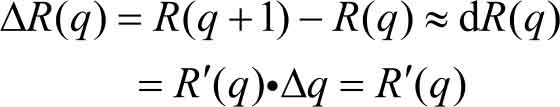
所以, 边际收入就是总收入关于销售量 q 的导数 。
(3) 边际利润
设某产品销售量为 q 时的总利润函数为 L = L ( q ),当 L ( q )可导时,称 L ′( q )为销售量 q 时的 边际利润 。它近似等于销售量为 q 时再多销售一个单位产品所增加(或减少)的利润。
由于总利润为总收入与总成本之差,即
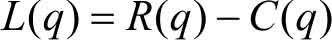
对上述等式两边求导,得
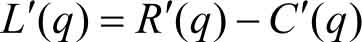
所以 边际利润为边际收入与边际成本之差 。
边际成本、边际收入、边际利润通常用MC、MR、ML表示。
例3.40
某商品产量为
x
(千升)时的成本函数为
C
(
x
)=
 (千元),其中0≤
x
≤5。求
x
=1,4时的边际成本,并给以适当的经济解释。
(千元),其中0≤
x
≤5。求
x
=1,4时的边际成本,并给以适当的经济解释。
解
边际成本函数
 。
。
当 x =1时,MC=1.5;当 x =4时,MC=0.75
这表明在生产1千升基础上再多生产1千升,需成本1.5千元;在生产4千升基础上再多生产1千升,仅需成本0.75千元,即产量越高,成本越低。
那么生产越多,赚的钱也越多吗?下面再看一个例子。
例3.41 某企业生产一种产品,每天的总利润 L ( x ) (元)与产量 x (kg)之间的函数关系为
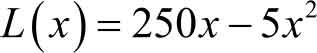
求 x =10,25,30时的边际利润,并给以适当的经济解释。
解 边际利润函数ML= L ′( x )=250-10 x 。
当 x =10时, L ′(10)=150 (元)。它表示,在每天生产10kg的基础上,再多生产1kg,总利润将增加150元。
当 x =25时, L ′(25)=0 (元)。它表示,在每天生产25kg的基础上,再多生产1kg,总利润几乎没有变化,这1kg产量并没有产生利润。
当 x =30时, L ′(30)=-50 (元)。它表示,在每天生产30kg的基础上,再多生产1kg,总利润就要减少50元。
从本题可以看出并非生产的产品数量越多,利润越高。
例3.42 某商品产量为 x 时的成本函数为 C ( x )= x 3 -3 x 2 +3 x ,求商品的边际成本和平均成本函数。
解
边际成本函数MC=
C
′(
x
)=3
x
2
-6
x
+3;平均成本函数
 =
x
2
-3
x
+3。
=
x
2
-3
x
+3。
从图3-7可以看出:在
 的区域内,
的区域内,
 下降;在MC=
下降;在MC=
 时,
时,
 达到最小值;在
达到最小值;在
 的区域内,
的区域内,
 上升。就是说:
最低平均成本与相应产量的边际成本相等
(本章只是用图像做直观分析,第4章还会就此做进一步分析)。
上升。就是说:
最低平均成本与相应产量的边际成本相等
(本章只是用图像做直观分析,第4章还会就此做进一步分析)。
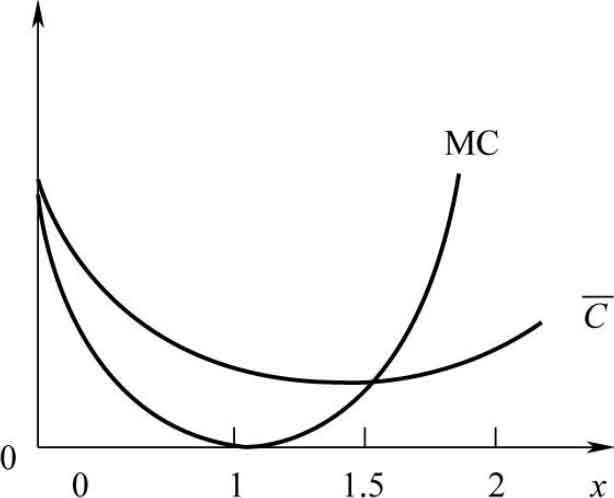
图3-7
3.相对变化率或弹性
上面提到变化率,但仅仅研究函数的绝对变化率是不够的。例如,商品甲、乙的单价分别为10元和1000元,它们各涨价1元,尽管绝对改变量一样,但各与其原价相比,两者涨价的百分比却有很大不同:商品甲涨了10%,而商品乙仅涨了0.1%。因此还须研究函数的相对变化率。
对于函数
y
=
f
(
x
)来说,Δ
y
、Δ
x
是函数、自变量的绝对改变量。
 是函数、自变量的相对改变量。
是函数、自变量的相对改变量。
定义3.3
对于函数
y
=
f
(
x
),当Δ
x
→0时,如果极限
 存在,则称此极限值为函数
f
(
x
)在点
x
处的
弹性
,记作
存在,则称此极限值为函数
f
(
x
)在点
x
处的
弹性
,记作
 。
。

由定义可以知,函数 y = f ( x )的弹性是函数的相对改变量与自变量的相对改变量比值的极限,它也被称为函数的 相对变化率 ,反映 f ( x )对 x 变化反应的强烈程度或敏感度。
4.需求弹性
在市场经济中,经常要分析一个经济量对另一个经济量相当变化的灵敏程度,这就是经济量的弹性。一般来说,商品的需求量对市场价格的反应是很灵敏的,刻画这种灵敏程度的量就是需求弹性。
由弹性的一般定义知:需求函数 Q = Q ( p )( Q 表示某商品的需求量, p 表示其市场价格)的弹性称为 需求弹性, 记作 ε p 。即

需要说明的是: 根据经济理论可知,需求函数为递减函数,所以 Q ′<0(有关知识第4章有详细说明),为了用正数表示需求弹性,故式中加了负号。
需求弹性 ε p 表示某商品的需求量 Q 对价格 p 的变动的反应程度:当商品的价格上涨(或下跌)1%时,其需求量将减少(或增加)。
当 ε p <1时,称为 低弹性 ,此时需求变动的幅度小于价格变动的幅度,价格变动对需求量的影响不大。
当 ε p >1时,称为 高弹性 ,此时需求变动的幅度大于价格变动的幅度,价格变动对需求量的影响较大。
当 ε p =1时,称为 单位弹性 ,此时需求变动的幅度等于价格变动的幅度。
例3.43 某产品滞销,准备通过降价扩大销路。如果该产品的需求弹性在1.7~2.1之间,试问当降价10%时,需求量(销售量)大约增加多少?

根据已知
 ,则
,则
当
ε
p
=1.7时,
 ;当
ε
p
=2.1时,
;当
ε
p
=2.1时,
 。
。
所以,需求量(销售量)大约增加17%~21%。
例3.44
设某商品的需求函数为
 (
Q
是需求量,
p
是价格),求
p
=2,4,6时的需求弹性,并给以适当的经济解释。
(
Q
是需求量,
p
是价格),求
p
=2,4,6时的需求弹性,并给以适当的经济解释。
解 需求弹性为
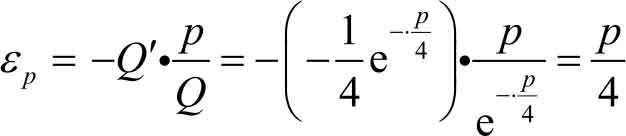
当 p =2时, ε p =0.5<1(低弹性),此时价格上涨(或下跌)1%,其需求量减少(或增加) 0.5%。
当 p =4时, ε p =1 (单位弹性),此时价格上涨(或下跌)1%,其需求量减少(或增加)1%。
当 p =6时, ε p =1.5>1(高弹性),此时价格上涨(或下跌)1%,其需求量减少(或增加) 1.5%。
习题3.5
1.某产品生产
x
单位时总成本
C
是
x
的函数
 ,求:
,求:
(1) 生产900单位时的总成本和平均成本;
(2) 生产900单位和1000单位时的边际成本。
2.设某厂每月生产的产品固定成本为 1000 元,生产 x 个单位产品的可变成本为0.01 x 2 +10 x 元,如果每单位产品的销售为 30 元,试求:①总成本函数;②总收入函数;③总利润函数;④边际成本;⑤边际收入;⑥边际利润为零时的产量。
3.设 p 为某产品的价格, x 为产品的需求量,且有 p =10-0.1 x 。求边际收入函数及 x =30,50,80时的边际收入,并解释所得结果的经济意义。
4.某企业的成本函数和收入函数如下。
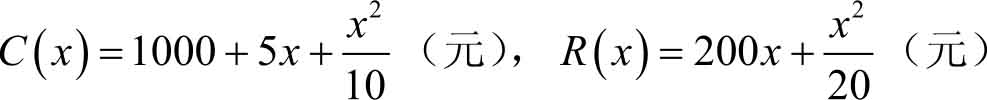
求:(1)边际成本,边际收入,边际利润。
(2)已生产并销售25个单位产品,销售第26个单位产品的利润。
5.设某商品的需求函数为 Q =600-50 p ( Q 是需求量, p 是价格)。求 p =1,6,8时的需求弹性,并给以适当的经济解释。
6.某产品因出口需要,拟用提价的办法压缩国内需求量的20%,如果该产品的需求弹性在1.5~2之间,试问应提价多少?


