1.1 函数的概念
1.1.1 常量与变量
在日常生活、生产活动和经济活动中,经常遇到各种不同的量,如身高、体重、收入、成本、气温、产量等。这些量可以分为两类:一类量在研究它的过程中不发生变化,只取一个固定的值,我们把它称为 常量 ,例如圆周率π以及某个成年人的身高、某种商品的价格在某一段时间内保持不变,这些量都是常量;另一类在研究它的过程中是变化的,可以取不同的数值,我们把它称为 变量 ,例如,一天中的气温与生产过程中的产量都是不断变化的,它们都是变量。
在理解常量与变量时,应注意以下几点。
(1) 常量与变量依赖于所研究的过程。同一个量,在某一特定的过程中可以认为是常量,而从长期来看则可能是变量;反过来也是这样。
(2) 从几何意义上讲,常量对应着实数轴上的定点,变量则对应着实数轴上的动点。
(3) 一个变量所能取的数值的集合叫做这个变量的 变动区域 。如果这个变量可以取介于两个实数之间的任意实数值,则称为 连续变量 。连续变量的变动区域常用区间表示。
常量习惯用字母 a 、 b 、 c 、 d 等表示;变量习惯用 x 、 y 、 z 、 u 、 v 、 w 等表示。
1.1.2 函数的概念及表示法
1.函数的概念
例如,一辆汽车以60km/h的速度匀速行驶,那么随着行驶时间 x 的变化,汽车行驶的里程 y 也随着发生变化,有这样的关系式 y =60 x ,我们称它为函数。
再如国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高。表1-1所示是我国城镇居民2006—2012年恩格尔系数变化情况。
表1-1 2006—2012年我国城镇居民恩格尔系数变化情况

从表中可以看出,对于每一年都有一个确定的恩格尔系数与之相对应,我们也称它为函数。
那么函数的概念是如何定义的呢?函数的概念在17世纪之前一直与公式紧密关联,到了1873年,德国数学家狄利克雷抽象出了直至今日仍为人们易于接受,并且较为合理的函数概念。
定义 1.1 设有两个变量 x , y ,若当变量 x 在实数的某一范围 D 内,任意取定一个数值时,变量 y 按照一定的对应规律 f ,都有唯一的值与它对应,则称变量 y 是变量 x 的 函数 ,记作
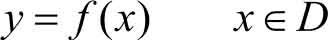
其中变量 x 称为自变量,变量 y 称为函数(或因变量)。自变量的取值范围 D 称为函数的定义域。
若对于确定的 x 0 ∈ D ,通过对应规律 f ,函数 y 有唯一确定的 y 0 相对应,则称 y 0 为 y = f ( x )在 x 0 处的函数值,记作
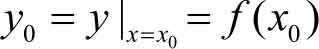
函数值的集合,称为函数的值域,记作 M 。
若函数在某个区间上的每一点都有定义,则称这个函数在该区间上有定义。
2.函数的两个要素
函数的对应规律和定义域称为函数的两个要素,而函数的值域一般称为派生要素。
(1) 对应规律
例1.1 f ( x )= x 2 +2 x -3是一个特定的函数, f 确定的对应规律为
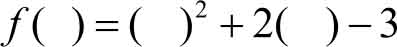
则 f (2)=2 2 +2×2-3; f (a)=(a) 2 +2(a)-3;…
例1.2
已知
 ,求
f
(0),
f
(
-x
),
,求
f
(0),
f
(
-x
),
 的值。
的值。
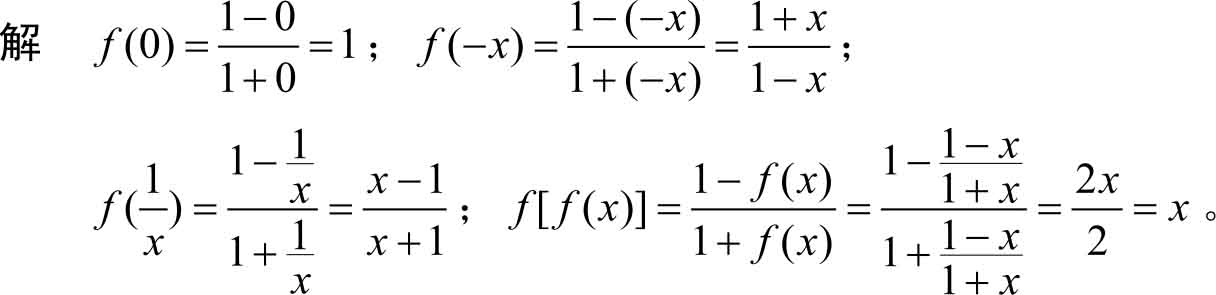
由于函数除用符号 f ( x )表示外,还常用 g ( x ), F ( x ), G ( x )等符号表示,因此对应关系 f 只是一个函数符号,在不同函数中, f 表示的具体对应规律是不一样的。
(2) 定义域
自变量的取值范围称为函数的定义域,给定一个函数,就意味着定义域同时给定了。定义域常用区间或集合来表示。
例1.3 求下列函数的定义域

解
(1) 要使分数
 有意义,分母不能为零,所以
x
(
x
-3)≠0,解得
x
≠0且
x
≠3,所以定义域为(-∞,0)∪(0,3)∪ (3,+∞)。
有意义,分母不能为零,所以
x
(
x
-3)≠0,解得
x
≠0且
x
≠3,所以定义域为(-∞,0)∪(0,3)∪ (3,+∞)。
(2) 在偶次根式中,被开方式必须大于等于零,即16 -x 2 ≥0,-4≤ x ≤4,所示定义域为[-4,4]。
(3) 在对数式中,真数必须大于零,即 x -1>0, x >1;又因为偶次方根式中,被开方式必须大于等于零,即ln( x -1)≥0, x -1≥1, x ≥2,所以定义域为 [2,+∞)。
(4) 反正弦或反余弦中的式子
φ
(
x
)的绝对值必须小于等于 1,即
 ,-7≤2
x
-1≤7,-3≤
x
≤4,所以定义域为[-3,4]。
,-7≤2
x
-1≤7,-3≤
x
≤4,所以定义域为[-3,4]。
请思考:
函数
 的定义域是什么?(定义域应是上述几个例子定义域的交集。)
的定义域是什么?(定义域应是上述几个例子定义域的交集。)
函数的定义主要包括定义域和对应规律,因此判定两个函数是否相同时,就要看定义域和对应规律是否完全一致,而由对应规律把它对应到了值域,且值域被唯一确定,为此判断两个函数是否相同就看其定义域和值域是否相同即可。
例1.4 判断下列各组函数是否是同一函数。
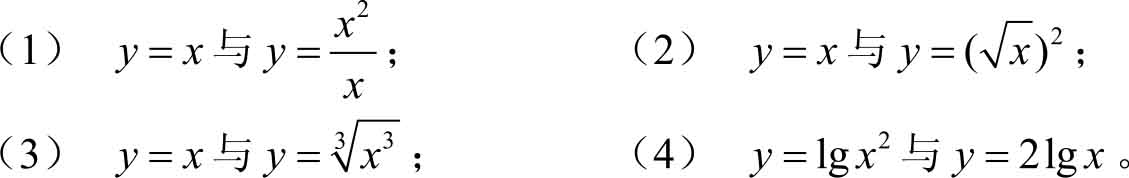
解
(1)不是同一函数。尽管它们的对应规律一样,但
y
=
x
的定义域是
R
,而
 的定义域是{
的定义域是{
 ∈
R
,且
x
≠0}。
∈
R
,且
x
≠0}。
(2) 不是同一函数。它们的定义域不同,
y
=
x
的定义域是
R
,而
y
=
 的定义域是[0,+∞)。
的定义域是[0,+∞)。
(3) 是同一函数。它们的定义域与值域都相同,因此是同一函数。
(4) 不是同一函数。它们的定义域不同, y =lg x 2 的定义域是 x ≠0的全体实数,而 y =2 lg x 的定义域是 x >0。
请思考: 下列各组函数是否是同一函数。
(1) f ( x )=1与 g ( x )= x 0 ;
(2) f ( x )=1与 g ( x )=sin 2 x +cos 2 x ;
(3) y = f ( x )与 x = f ( y )。
3.函数的表示法
函数的表示方法,常用的有解析法、列表法、图像法三种。
(1) 解析法
就是把两个变量的函数关系,用一个等式来表示,又称公式法。
例如 y = ax 2 + bx + c ( a ≠0); A =π r 2 等都是用解析法表示函数关系的。
解析法的优点是函数关系清楚,容易从自变量的值求出其对应的函数值,便于用解析式来研究函数的性质。
(2) 列表法
就是列出表格来表示两个变量的函数关系。
例如,银行常用的“利息表”、三角函数表、产品销售量表,等等。
又如,表1-1所示的我国城镇居民2006—2012年恩格尔系数变化情况。
列表法表示函数关系的优点是不必通过计算就知道当自变量取某值时函数的对应值。
(3) 图像法
就是用函数图像表示两个变量之间的关系。图1-1所示是我国1990—2006年国内生产总值增速变化曲线。
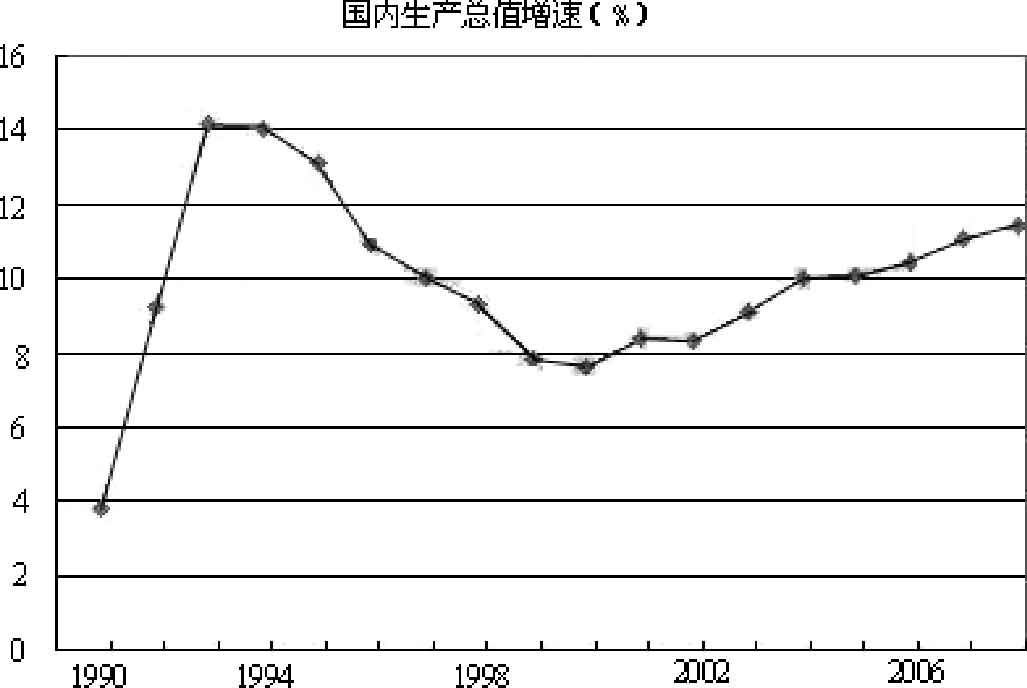
图1-1
图像法表示函数关系的优点是能直观形象地表示出函数的变化情况。
4.分段函数
某市移动通信公司有一款优惠套餐,规定收费标准为:当月所打电话时长不超过40分钟时,只收取月租费15元,超过40分钟,每分钟加收0.12元。电话费 y (元)和用户当月所打电话的时长 x (分钟)的关系可用下面的形式给出:
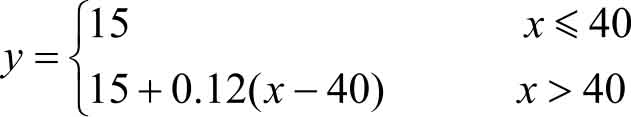
像这样把定义域分成若干部分,函数关系由不同的式子分段表达的函数称为 分段函数 。分段函数是定义域上的一个函数,不要理解为多个函数,分段函数需要分段求值,分段作图。其定义域为各分段部分定义域的并集。
例1.5 设有以下分段函数:
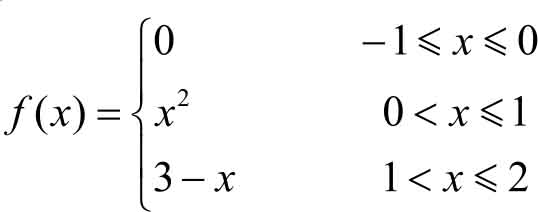
求:(1)函数值 f (-0.5), f (0.5), f (1.5);(2)函数的定义域;(3)画出该分段函数的图像。
解 (1) f (-0.5)=0; f (0.5)=0.5 2 =0.25; f (1.5)=3-1.5=1.5。
(2) 由于其定义域为各分段部分定义域的并集,所以 f ( x )的定义域为[-1,2]。
(3) 该分段函数的图像如图1-2所示。
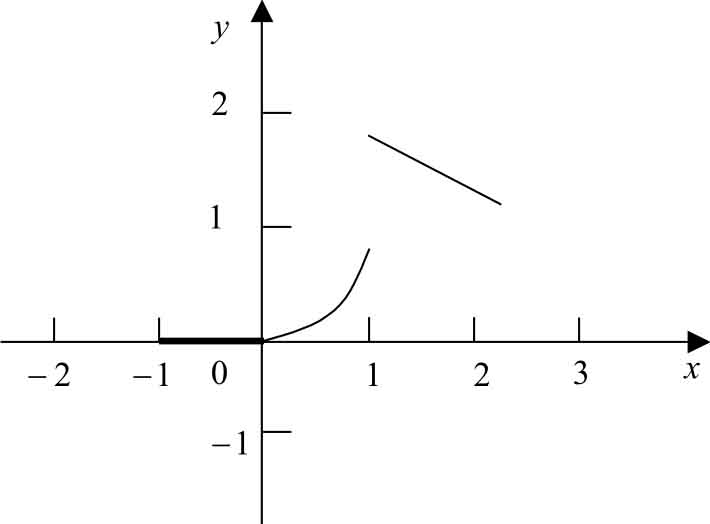
图1-2
例1.6 2011年9月1日开始实施新的《中华人民共和国个人所得税法》,个税免征额调至3500元,如表1-2所示。
表1-2 个人所得税率表(工资、薪金所得适用)
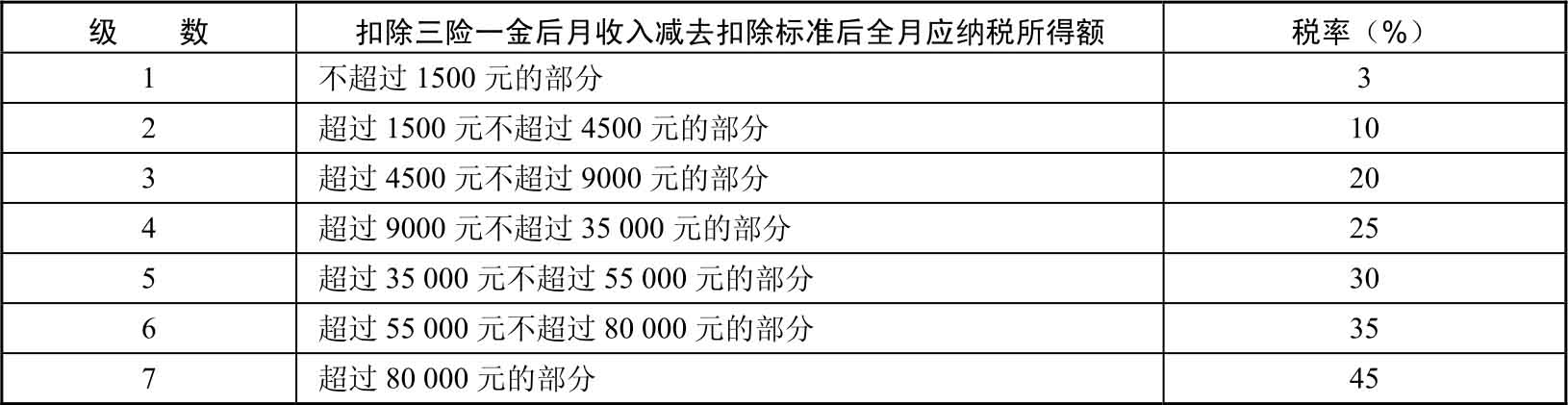
目前,在表1-2中全月应纳税所得额是从工资、薪金收入中减去3500元后的余额。例如,某人扣除三险一金后月工资、薪金收入6000元,减去3500元,应纳税所得额为2500元,由税率表可知,其中1500元税率为3%,另1000元税率为10%,所以此人应纳个人所得税为1500×3%+1000×10%=145元。
请写出月工资、薪金的个人所得税 y 关于工资、薪金收入 x (0< x ≤10 000) 的函数表达式。
解 这个函数的定义域为 (0,+∞),自变量 x (0< x ≤10 000) 的解析表达式如下。

例1.7 为配合客户不同需要,某移动通信公司推出A、B两种优惠计划供客户选择,如表1-3所示。根据提供信息,解答下列问题。
表1-3 某通信公司推出A、B两种计划比较表

(1)设通话时间为 x 分钟,所需付出的费用为 y 元,分别写出计划A、计划B中 y 与 x 之间的函数关系式。
(2) 通话时间超过多少分钟时,计划B会比计划A更省钱?
(3) 在直角坐标系中画出A、B计划所对应得函数图像。
解 (1) 计划A:
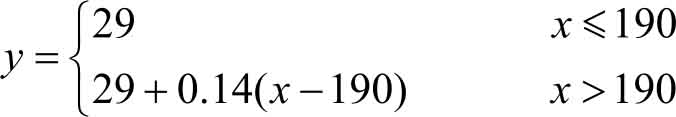
计划B:
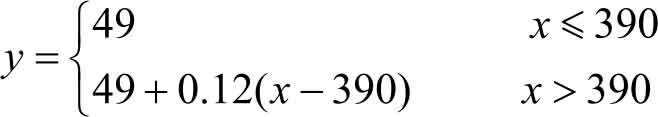
(2) 要使计划B比计划A省钱,即29+0.14( x -190)>49,解得 x >333。
(3) 两个计划的图像如图1-3所示。
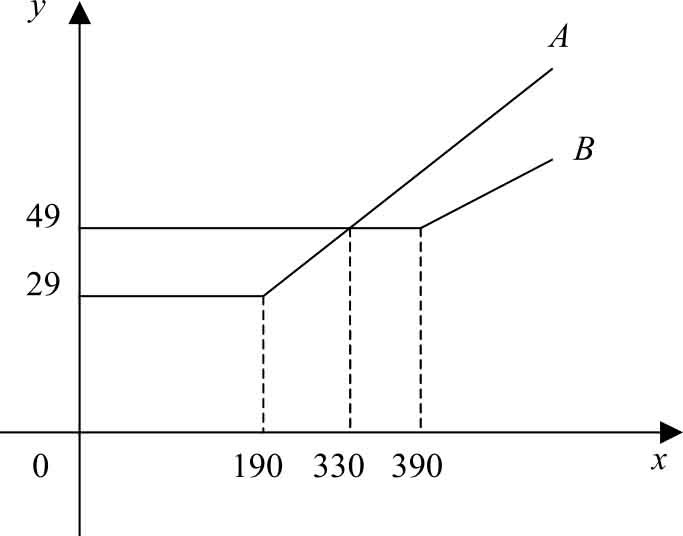
图1-3
习题1.1
1.判断下列各对函数是否是同一函数。
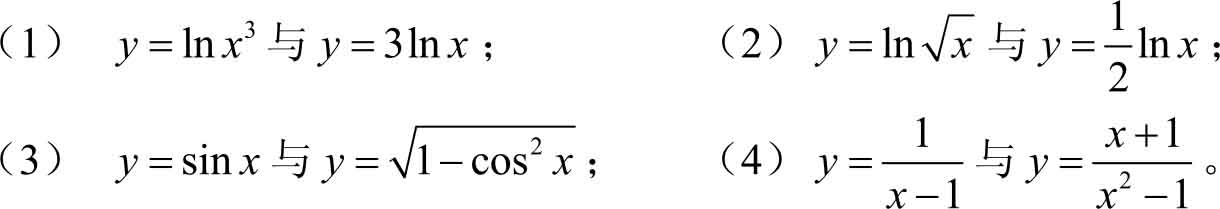
2.求下列函数的定义域。
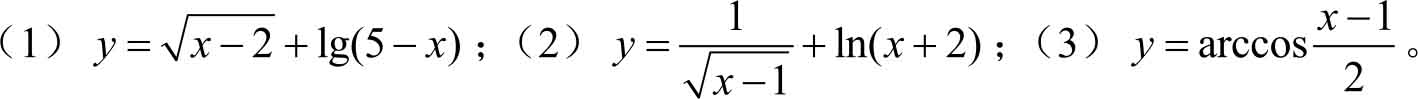
3.设函数

求:(1) f (-1), f (3), f (4), f (6)的函数值;
(2) 函数 f ( x )的定义域;
(3) 作出函数的图像。


