1.4 初等函数
微积分的研究对象主要是初等函数,而初等函数是由基本初等函数构成的。基本初等函数包括常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数六大类。虽然大部分函数在中学已经学过,但我们在这里对它们重新分类,并重点掌握它们的定义域、值域、图像和性质。
1.4.1 基本初等函数
1.常数函数 y = C ( C 为常数)
它的定义域是(-∞,+∞),由于无论 x 取何值,都有 y = C ,所以,它的图像是过(0, C )平行于 x 轴的一条直线。如图1-10所示,它是偶函数。
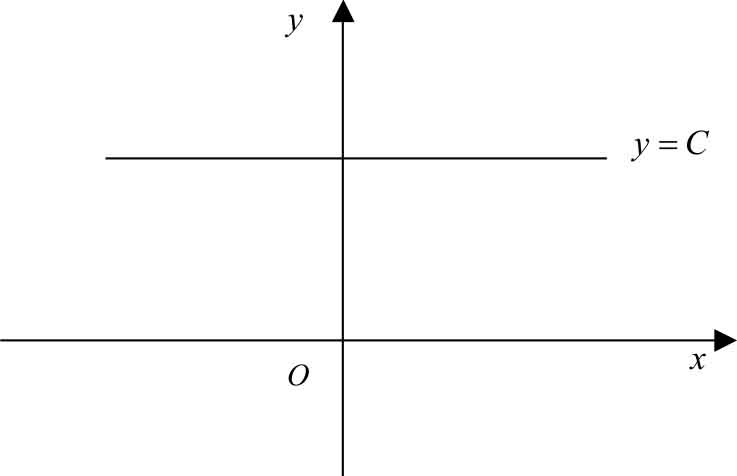
图1-10
2.幂函数 y = x u ( u ∈R)
幂函数的情况比较复杂,我们分 u >0和 u <0两种情况来讨论。
当 u 取不同值时,幂函数的定义域不同,为了便于比较,我们只讨论 x >0的情况,而 x <0的图像可根据函数的奇偶性确定。
当
u
>0时,取
u
=1、2、3、
 ,我们可以看到函数图像通过原点(0,0)和点(1,1),在(0,+∞)内单调增加且无界,如图1-11所示。
,我们可以看到函数图像通过原点(0,0)和点(1,1),在(0,+∞)内单调增加且无界,如图1-11所示。
当
u
<0时,取
 -1、-2,我们可以看到图像不过原点,但仍通过(1,1),在(0,+∞)内单调减少,无界,曲线以
x
轴和
y
轴为渐近线,如图1-12所示。
-1、-2,我们可以看到图像不过原点,但仍通过(1,1),在(0,+∞)内单调减少,无界,曲线以
x
轴和
y
轴为渐近线,如图1-12所示。
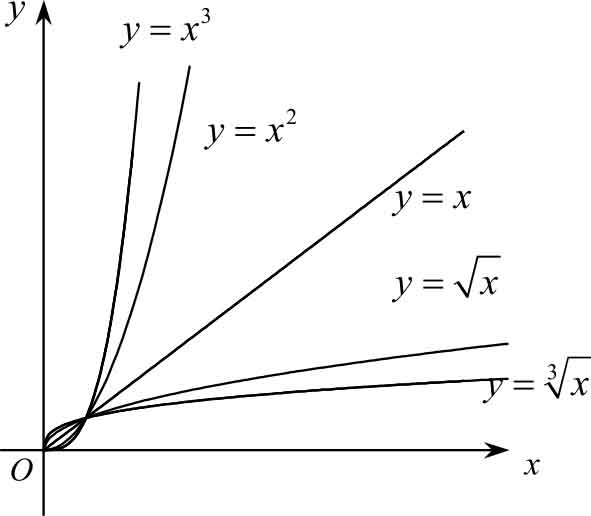
图1-11
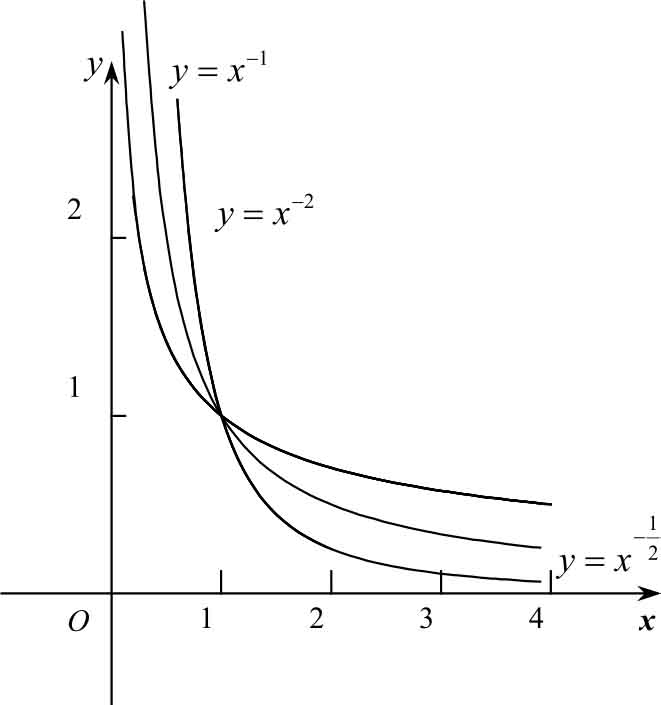
图1-12
3.指数函数 y = a x ( a >0, a ≠1)
它的定义域为(-∞,+∞),由于无论 x 取何值,总有 a x >0,且 a 0 =1,因此指数函数的图像全部在 x 轴上方,且通过(0,1)点,也就是说,它的值域是(0,+∞)。
例1.12
画出
y
=2
x
,
 的图像。
的图像。
解 列表1-4,用描点法画图。
表1-4 y =2 x 和 y =2 - x 的变化情况表

从图1-13中可以看出, y =2 x 的图像与 y =2 -x 的图像是关于 y 轴对称的。
通过例1.12我们可知,对于指数函数:当 a >1时,函数单调增加且无界,曲线以 x 轴负半轴为渐近线;当0< a <1时,函数单调减少且无界,曲线以 x 轴正半轴为渐近线。
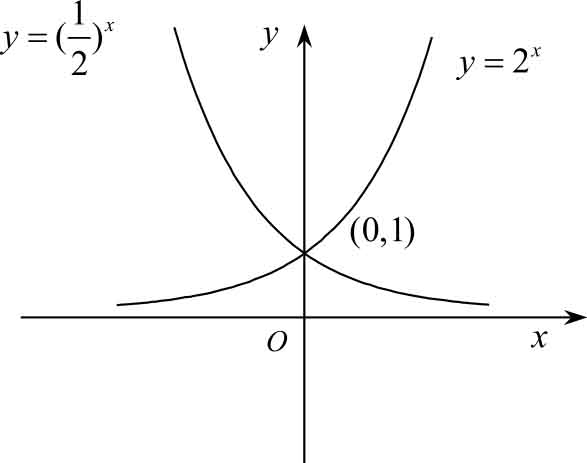
图1-13
4.对数函数 y =log a x ( a >0, a ≠1)
“对数源于指数”,即对数函数 y =log a x 是指数函数 y = a x 的反函数,因此对数函数与指数函数的图像是关于直线 y = x 对称。
例1.13 在同一坐标系中画出下列函数的图像。
(1) y =2 x 与 y =log 2 x ;
(2
 .
.
解
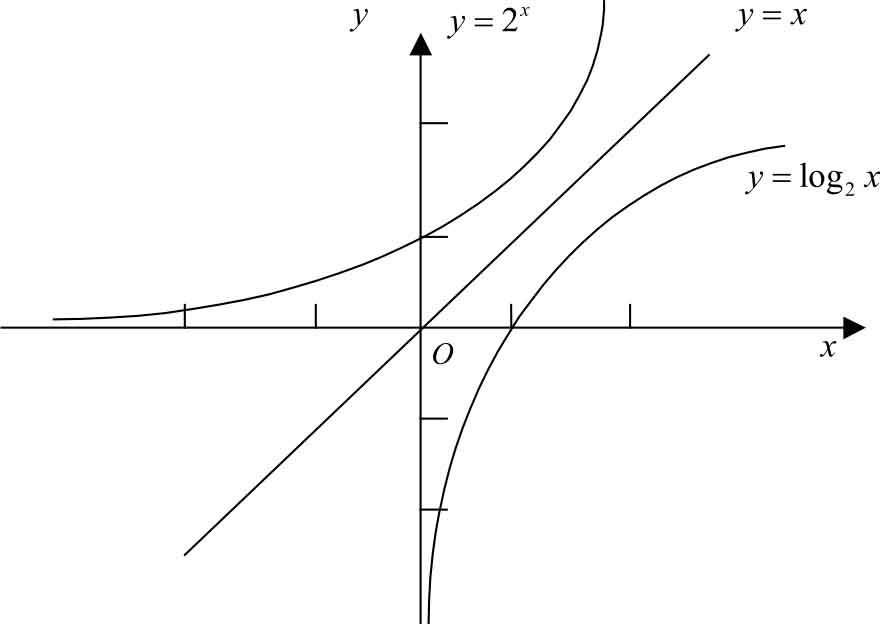
图1-14
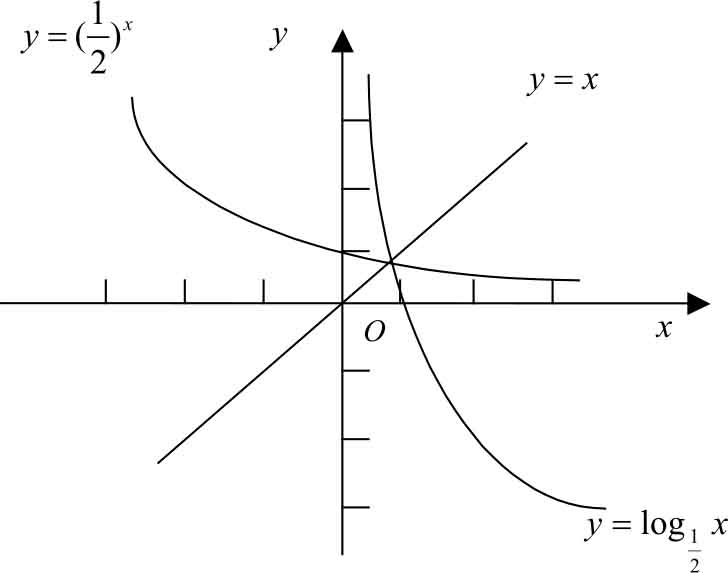
图1-15
从图1-14所示函数
y
=2
x
与
y
=log
2
x
的图像和图1-15所示函数
 的图像可以看出,它们是关于直线
y
=
x
的对称函数。
的图像可以看出,它们是关于直线
y
=
x
的对称函数。
因此,对数函数的定义域是(0,+∞),图像全部在 y 轴的右方,值域是(-∞,+∞),无论 a 取何值,曲线都通过点(1,0)。
当 a >1时,函数是单调增加且无界,曲线以 y 轴负半轴为渐近线;当0< a <1时,函数单调减少且无界,曲线以 y 轴正半轴为渐近线。
通常将以 10 为底的对数函数叫做 常用对数 函数,记作 y =log 10 x =lg x ;以无理数e=2.718 281 8…为底的对数函数 y =log e x 叫做 自然对数 函数,记作 y =log e x =ln x ,自然对数函数是微积分中常用的函数。
5.三角函数
三角函数包括下面六个函数。
(1) 正弦函数 y =sin x ;
(2) 余弦函数 y =cos x ;
(3) 正切函数 y =tan x ;
(4) 余切函数 y =cot x ;
(5) 正割函数
 ;
;
(6) 余割函数
 。
。
在微积分中,三角函数的自变量 x 采用弧度制,弧度与角度的换算公式如下。
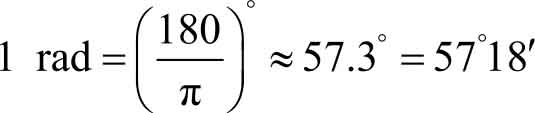
下面分别介绍六个三角函数的特点和性质。
(1) 正弦函数 y =sin x
它的定义域为(-∞,+∞),值域为[-1,1],当
 (
k
∈
Z
)时取得最大值1,当
(
k
∈
Z
)时取得最大值1,当
 (
k
∈
Z
)时取得最小值-1。它是奇函数,是以 2π为周期的周期函数,有界。如图1-16所示。
(
k
∈
Z
)时取得最小值-1。它是奇函数,是以 2π为周期的周期函数,有界。如图1-16所示。
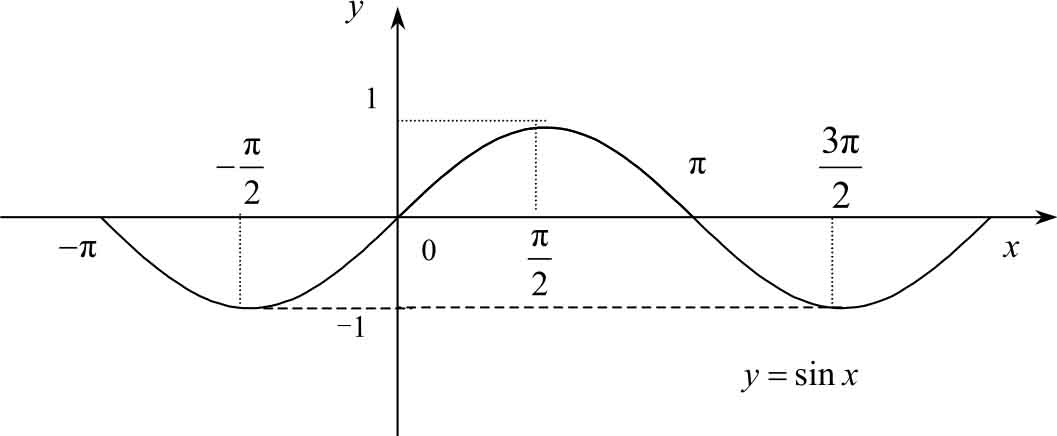
图1-16
(2) 余弦函数 y =cos x
它的定义域为(-∞,+∞),值域为[-1,1],当 x =2 k π ( k ∈ Z )时取得最大值 1,当 x =2 k π+π ( k ∈ Z )时取得最小值-1。它是偶函数,是以2π为周期的周期函数,有界。如图1-17所示。
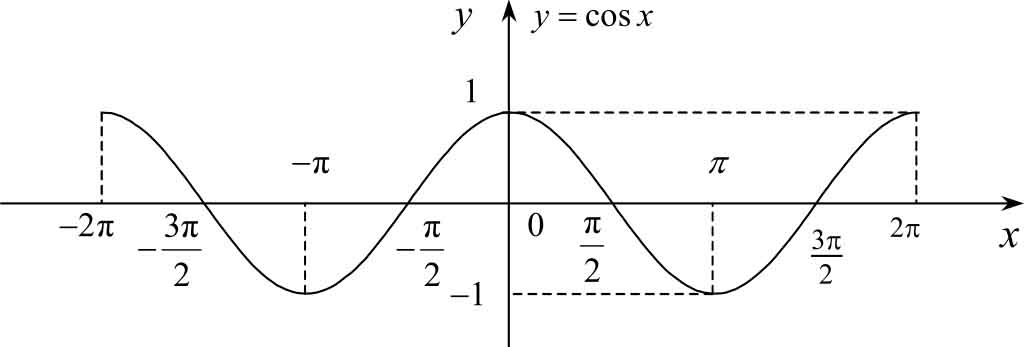
图1-17
(3) 正切函数 y =tan x
它的定义域为
 (
k
=0,±1,±2,…),值域为(-∞,+∞)。以π为周期,在每个周期内单调增加,以直线
(
k
=0,±1,±2,…),值域为(-∞,+∞)。以π为周期,在每个周期内单调增加,以直线
 (
k
=0,±1,±2,…)为渐近线。如图 1-18所示。
(
k
=0,±1,±2,…)为渐近线。如图 1-18所示。
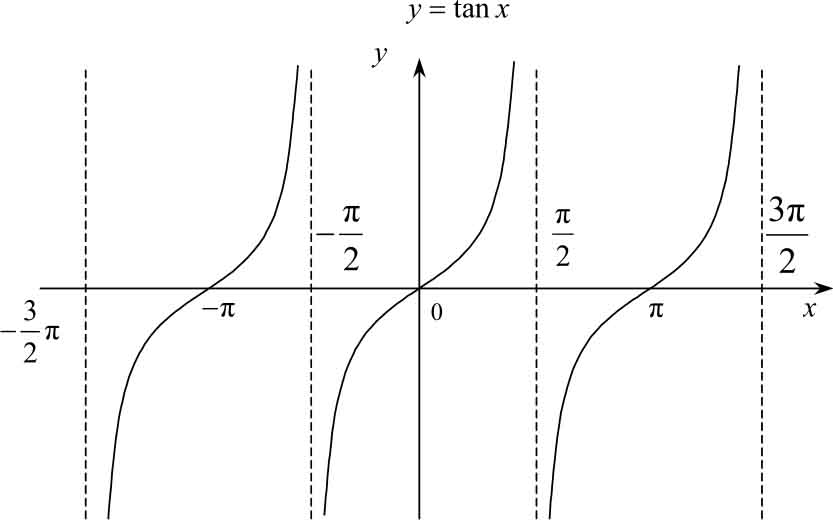
图1-18
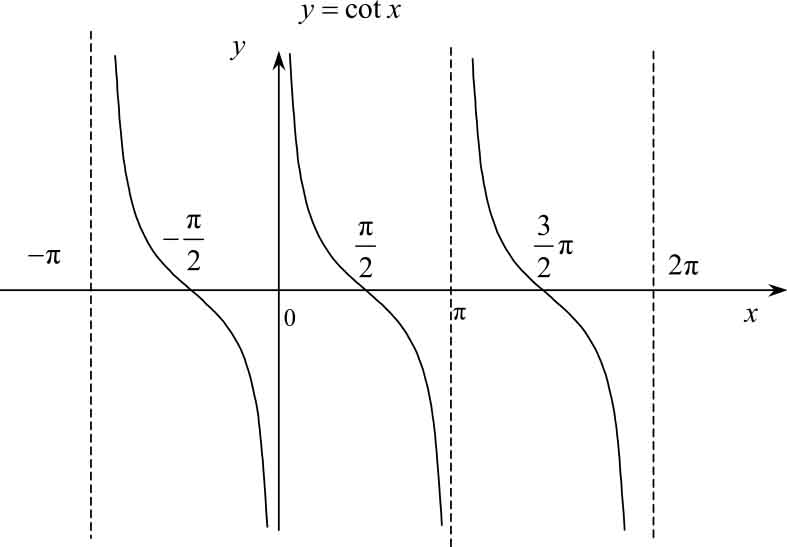
图1-19
(4) 余切函数 y =cot x
它的定义域为 x ≠ k π ( k =0,±1,±2,…),值域为(-∞,+∞)。它以π为周期,在每个周期内单调减少,以直线 x = k π ( k =0,±1,±2,…)为渐近线,如图1-19所示。
关于函数
y
=sec
x
和
y
=csc
x
,我们不作讨论,只需知道
 之间的关系就可以了。
之间的关系就可以了。
6.反三角函数
常用的反三角函数有以下四个。
(1) 反正弦函数 y =arcsin x ;
(2) 反余弦函数 y =arccos x ;
(3) 反正切函数 y =arctan x ;
(4) 反余切函数 y =arc cot x 。
它们是作为相应三角函数的反函数定义出来的。
y
=arcsin
x
的含义是正弦值等于
x
的角,与三角函数相反,这里自变量
x
表示正弦值,而
y
则表示角,准确的说是角的弧度数。例如
y
=
 表示正弦值为
表示正弦值为
 的角,我们知道
的角,我们知道
 的正弦值是
的正弦值是
 ,所以有
,所以有
 。但实际上,
。但实际上,
 (
k
=0,±1,±2,…)的正弦值都是
(
k
=0,±1,±2,…)的正弦值都是
 ,这与我们前面讲的函数的定义不符合,为了避免
y
=arcsin
x
的多值性,我们限定了一个区间
,这与我们前面讲的函数的定义不符合,为了避免
y
=arcsin
x
的多值性,我们限定了一个区间
 ,叫做反正弦函数的
主值区间
。在这个区间内,自变量
x
与函数值
y
之间建立了一一对应的关系。
,叫做反正弦函数的
主值区间
。在这个区间内,自变量
x
与函数值
y
之间建立了一一对应的关系。
类似地,其他几种反三角函数都规定了相应的主值区间,保证了它们的单值性。当然,由于函数的性质不同,它们的主值区间范围不同。今后在本书中凡不做特殊说明的反三角函数都是指在它们主值区间内。
下面讨论四个反三角函数的特点和性质。
(1) y =arcsin x
它的定义域为[-1,1],值域为
 。它是单调增函数,奇函数,有界。其图像如图1-20所示。
。它是单调增函数,奇函数,有界。其图像如图1-20所示。
(2) y =arccos x
它的定义域为[-1,1],值域为[0,π]。它是单调减函数,有界。其图像如图1-21所示。
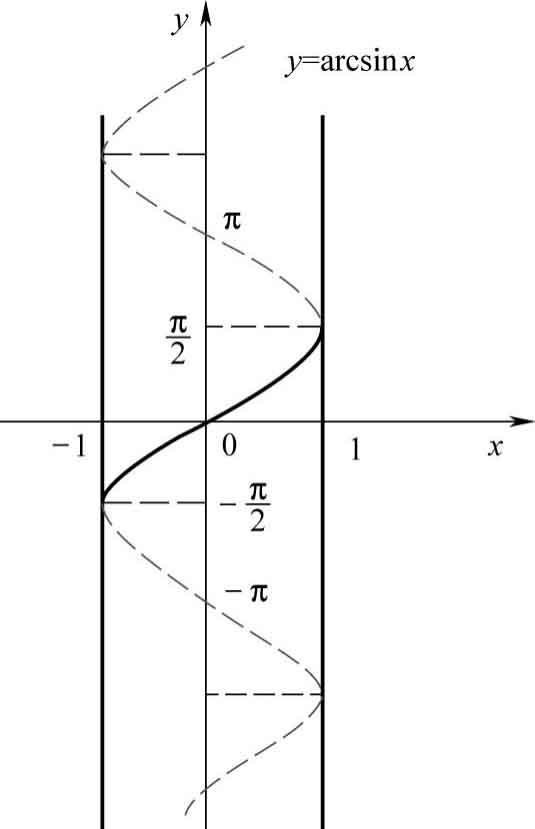
图1-20
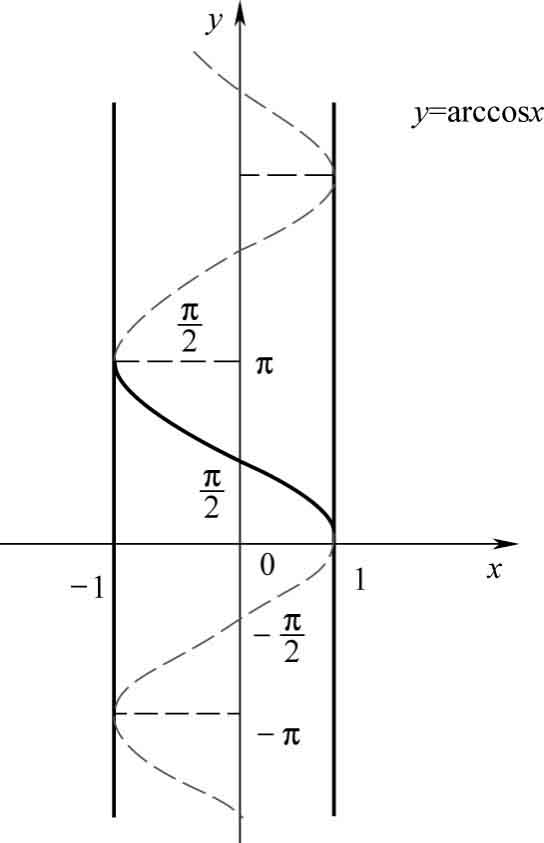
图1-21
(3) y =arctan x
它的定义域为(-∞,+∞),值域为
 。它是单调增函数,奇函数,有界。其图像如图1-22所示。
。它是单调增函数,奇函数,有界。其图像如图1-22所示。
(4) y =arc cot x
它的定义域为(-∞,+∞),值域为(0,π)。它是单调减函数,有界。其图像如图 1-23所示。
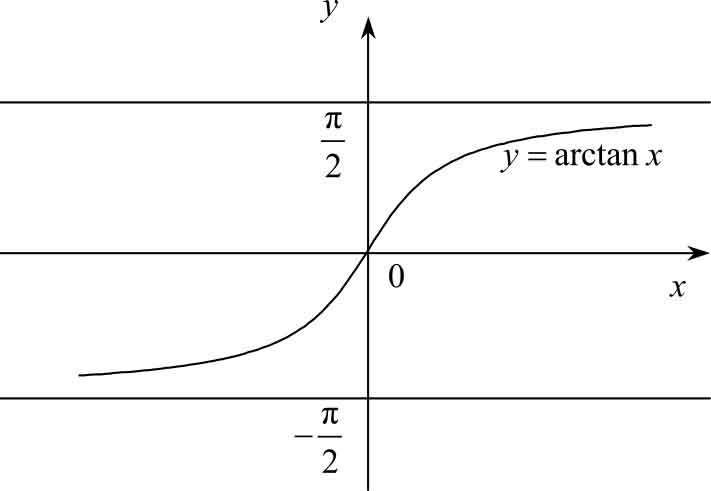
图1-22
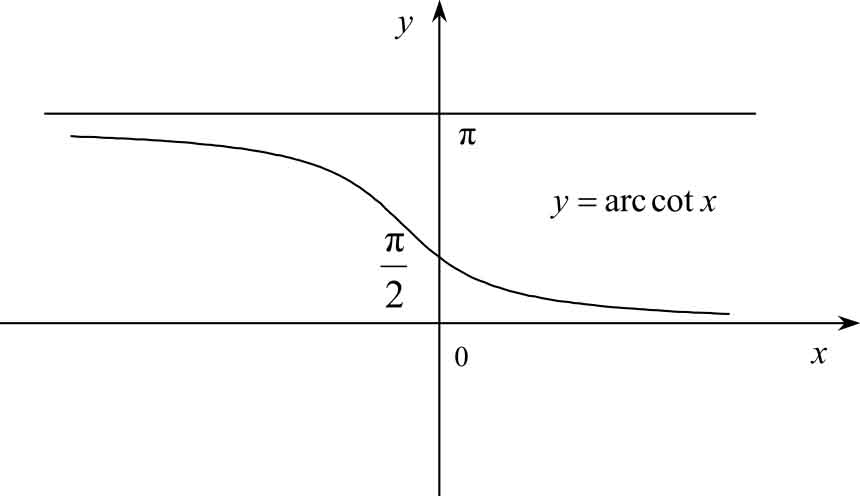
图1-23
1.4.2 复合函数与初等函数
1.复合函数
在实际经济活动中,我们会遇到这样的问题:一般来说成本 c 可以看做产量 q 的函数,而产量 q 又是时间 t 的函数,时间 t 通过产量 q 间接影响成本 c ,那么成本 c 仍然可以看做时间 t 的函数。 c 与 t 的这种函数关系称做一种复合的函数关系,产量 q 可以看做这种复合关系的中间变量。
定义1.2 设 y 是 u 的函数 y = f ( u ), u 是 x 的函数 u = φ ( x )。如果 u = φ ( x )的值域全部或其部分包含在 y = f ( u )的定义域中,则 y 通过中间变量 u 构成 x 的函数,称为 x 的 复合函数 ,记作
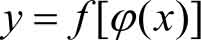
其中, x 是自变量, u 称做中间变量。
对于复合函数,我们做如下说明。
(1) 不是任何两个函数都可以复合成一个复合函数。
例如,
y
=lg
u
,
 就不能复合成一个复合函数,因为
就不能复合成一个复合函数,因为
 ,在其定义域[1,+∞)中,任何
x
的取值所对应
u
值均为非正数,它们都不可能落在
y
=lg
u
的定义域(0,+∞)内,所以
y
=lg
u
与
u
=
,在其定义域[1,+∞)中,任何
x
的取值所对应
u
值均为非正数,它们都不可能落在
y
=lg
u
的定义域(0,+∞)内,所以
y
=lg
u
与
u
=
 不能复合成一个复合函数。
不能复合成一个复合函数。
(2) 复合函数不仅可以由两个函数,还可以由两个以上的函数复合而成。例如
 就是由
y
=ln
u
,
u
=
x
+
v
,
就是由
y
=ln
u
,
u
=
x
+
v
,
 ,
w
=1+
x
2
四个函数复合而成的,其中
u
,
v
,
w
都是中间变量。
,
w
=1+
x
2
四个函数复合而成的,其中
u
,
v
,
w
都是中间变量。
我们不仅要研究函数的复合,而且还要研究函数的分解,在分解函数时,首先要认真地分析一个复合函数的构成,搞清楚它的复合关系和复合层次,然后由外往里一层层地顺次分解,将各层次分解为基本初等函数或由基本初等函数经过有限次四则运算形成的简单函数。因此说复合函数的合成和分解往往是对简单函数而言的。
例1.14 已知 y =ln u , u =sin x ,将 y 表示成为 x 的函数。
解 将 u =sin x 代入 y =ln u 中,可得
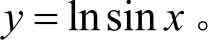
例1.15 已知 y =ln u , u =4 -v 2 , v =sin x ,将 y 表示成为 x 的函数。
解 y =ln(4 -v 2 )=ln(4-sin 2 x )。
例1.16 指出下列函数是由哪些简单函数复合而成的:
(1

(2
 .
.
解
(1)设
y
=
 ,
u
=sin
v
,
,
u
=sin
v
,
 。则
。则
 是由
y
=
是由
y
=
 ,
u
=sin
v
,
,
u
=sin
v
,
 复合而成的。
复合而成的。
(2) 设
y
=5
u
,
u
=cos
v
,
 。则
。则
 是由
y
=5
u
,
u
=cos
v
,
是由
y
=5
u
,
u
=cos
v
,
 复合而成的。
复合而成的。
2.初等函数
定义1.3 由六类基本初等函数经过有限次四则运算或有限次复合而成的函数叫做 初等函数 。
一般来说,初等函数都可以用一个解析式子表示。
例如,
 ;
y
=arcsin[cos
2
(
x
3
+
x
)]都是初等函数。今后我们在讨论函数时,绝大多数指的是初等函数。
;
y
=arcsin[cos
2
(
x
3
+
x
)]都是初等函数。今后我们在讨论函数时,绝大多数指的是初等函数。
而
y
=1+
x
+
x
2
+
x
3
+…不满足有限次运算和分段函数
 一般都不是初等函数。
一般都不是初等函数。
习题1.4
1.写出所给函数的复合函数。
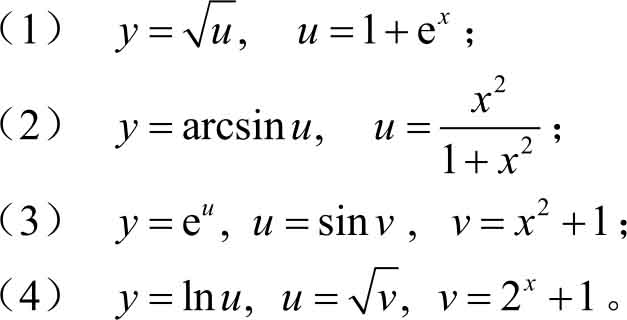
2.指出下列函数是由哪些简单函数复合而成的。
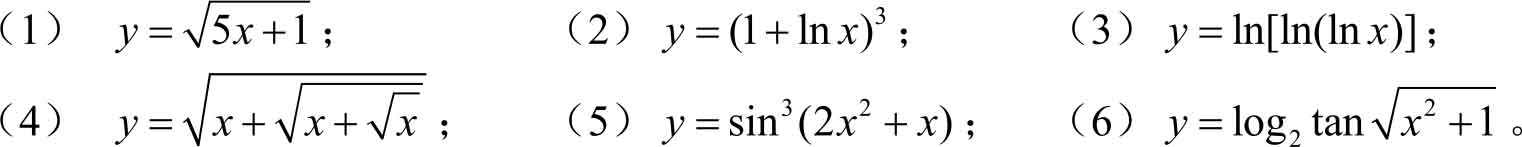
3.在同一坐标系上画出 y = x 3 , y = x 3 +1, y =( x +1) 3 +1的图像,并从图像上观察三个函数的关系。


