1.5 常用经济函数
我们知道,函数是描述客观世界变化规律的基本数学模型,不同的变化规律需要用不同的函数模型来描述。经济函数就是用数学方法解决经济问题,找出经济变量之间的函数关系,建立数学模型。
下面介绍几种常用的经济函数。
1.5.1 需求函数与供给函数
1.需求函数
“ 需求 ”是指在一定条件下,人们愿意购买并且有支付能力购买的商品量。人们对某种商品的需求是由多种因素决定的,如收入、商品的价格、季节、地区等。当我们的目的是研究需求量 Q 与商品价格 p 之间的依赖关系时,常常把需求量的其他影响因素固定在某一常数上,这样需求量 Q 可以看成是价格 p 的一元函数,称为 需求函数 。记作

一般来说,降低商品的价格,需求量增加;提高商品的价格,需求量减少。因此说,需求函数为价格 p 的单调减少函数。
常见的需求函数模型如下。
(1) 线性函数形式: Q = b-ap ( a >0, b >0);
(2) 反比函数形式:
 (
k
>0,
p
≠0);
(
k
>0,
p
≠0);
(3) 二次函数形式: Q = a-bp-cp 2 ( a >0, b >0, c >0);
(4) 幂函数形式:
 (
u
>0,
k
>0,
p
≠0);
(
u
>0,
k
>0,
p
≠0);
(5) 指数函数形式: Q = a e -bp ( a >0, b >0)。
需求函数 Q = Q ( p )的反函数,就是 价格函数 ,记作
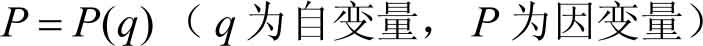
价格函数也是一个单调减少函数,也能反映出商品的需求与价格的关系。
2.供给函数
“ 供给 ”是指在一定价格条件下,生产者愿意出售并且有可能提供出售的商品量。
供给与需求是相对的概念,需求是对购买者而言,供给是对生产者而言。供给也是由许多因素决定的,如果略去价格 p 以外的其他影响因素,则商品的供给量 S 也是价格 p 的一元函数,称为 供给函数 ,记作
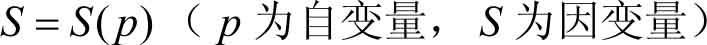
一般来说,价格上涨,生产者愿意向市场提供更多的商品,使供给量增加;反之,价格下跌,将使供给量减少。因此说,供给函数为价格 p 的单调增加函数。
常见的供给函数模型如下。
(1) 线性函数形式: S = ap-b ( a >0, b >0);
(2) 幂函数形式: S = kp u ( u >0, k >0, p ≠0);
(3) 指数函数形式: S = ae bp ( a >0, b >0)。
3.均衡价格与均衡商品量
如果市场上某种商品的需求量恰好等于供给量,则称该商品在市场上处于均衡状态。此时商品的价格称为 均衡价格 ,商品的需求量(或供给量)称为 均衡商品量 。如图1-24所示。
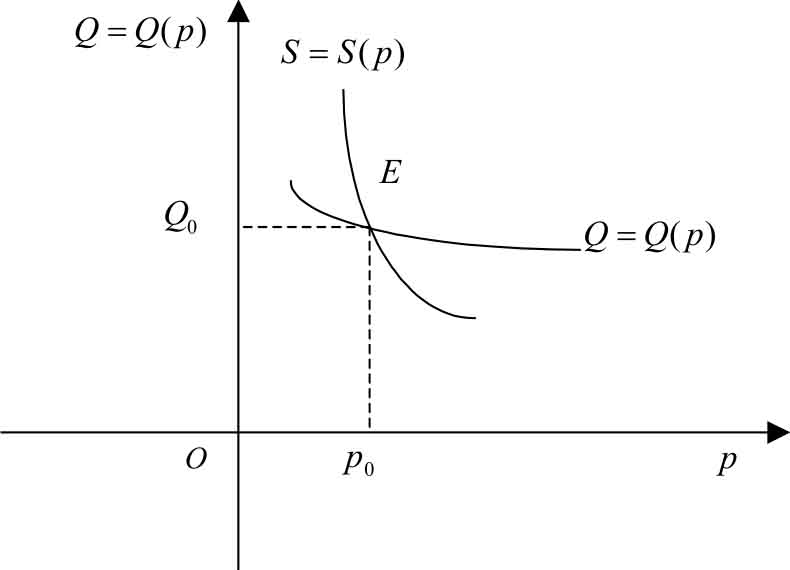
图1-24
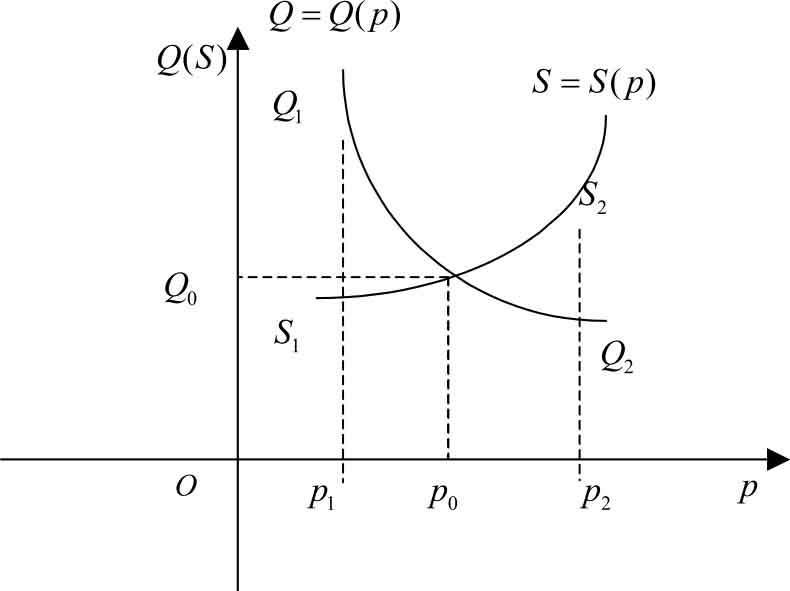
图1-25
需求曲线 Q = Q ( p )与供给曲线 S = S ( p )的交点 E 的横坐标 p = p 0 就是均衡价格,交点 E 的纵坐标 Q = Q 0 (或 S = S 0 )就是均衡商品量。
当 p < p 0 ,如图1-25中的 p = p 1 处,此时消费者希望购买的商品量 Q 1 大于生产者愿意出售的商品量 S 1 ,即 Q 1 > S 1 ,这时市场出现“供不应求”现象,商品短缺,会形成抢购、黑市等情况,这种状况不会持久,必然导致价格上涨。
当 p > p 0 ,如图1-25中的 p = p 2 处, Q 2 < S 2 ,这时市场出现“供过于求”现象,商品滞销,这种状况也不会持久,必然导致价格下跌。
总之,在货币稳定的环境中,市场上的商品价格将围绕着均衡价格摆动。
例1.17 当鸡蛋收购价格为6.0/kg元时,某收购站每月能收购5 000kg,若收购价格提高0.2元/kg,则收购量可增加400kg。求鸡蛋的线性供给函数。
解 设鸡蛋的线性供给函数为

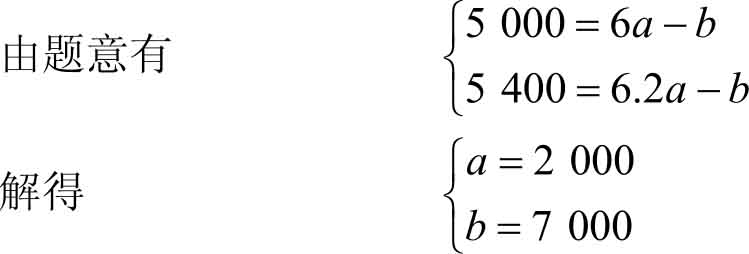
所求供给函数为

例1.18 已知某种商品的需求函数 Q =10-2 p ,供给函数为 S =5 p -4,求均衡价格 p 0 与均衡商品量 Q 0 。
解 由供需均衡条件 Q = S 可得
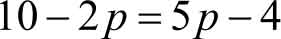
解得 p =2,代入 Q =10-2 p 中得 Q =6。所以,均衡价格 p 0 =2,均衡商品量 Q 0 =6。
1.5.2 总成本函数、总收入函数及总利润函数
在生产和产品经营活动中,人们总希望尽可能降低成本,提高收入和利润。而成本、收入和利润这些经济变量都与产品的产量或销售量 q 密切相关,它们都可以看作是 q 的函数。现在我们分别介绍如下。
1.总成本函数与平均成本函数
总成本 是指生产一定数量的某种产品所投入的费用总额。它分为固定成本和可变成本两部分,固定成本与产量 q 无关,如设备维修费、企业管理费用等,常用 C 1 表示;可变成本随产量 q 的增加而增加,如原材料费、动力费等,常用 C 2 表示,记作 C 2 ( q )。我们称
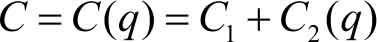
为 总成本函数 ,其中 C 表示总成本, q 表示产量。
总成本函数 C 是产量 q 的单调增加函数。
常采用的函数模型如下。
(1) 线性成本函数: C = a + bq ( a >0, b >0);
(2) 三次需求函数: C = a 0 + a 1 q-a 2 q 2 + a 3 q 3 ( a i >0, i =1,2,3)。
只给出总成本不能说明企业生产的好坏,为了评价企业的生产状况,需要计算产品的平均成本。即生产
q
个单位产品时,单位产品成本的平均值,记作
 ,则
,则
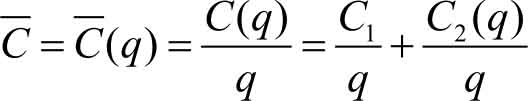
其中,
 称为
平均可变成本
。
称为
平均可变成本
。
例1.19
已知某种产品的总成本函数为
 ,求当生产30个该产品时的总成本和平均成本。
,求当生产30个该产品时的总成本和平均成本。
解 由题意,产量为30个时的总成本为
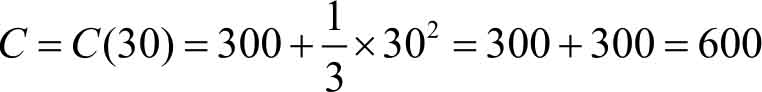
产量为30个时的平均成本为
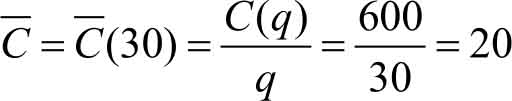
2.总收入和平均收入函数
总收入 是指销售者按照某种价格售出一定数量商品所得的全部收入。即销售的价格与销售量的乘积。我们称
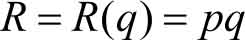
为 总收入函数。 其中 R 表示总收入, q 表示销售量, p 表示商品的价格,为常数。
在市场经济环境中,价格 p 不一定是常数,价格是随着需求量改变而变动的,因此说价格 p 是销售量 q 的函数,即 p = p ( q ) (如当买主购买的商品数量 q 越大时,卖主所要的商品的价格越低),则此时的总收入函数又可表示为
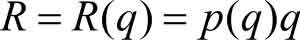
平均收入是指售出一定数量商品时,售出单位商品的平均价格。我们称
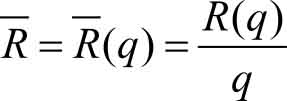
为
平均收入函数
,其中
 表示平均收入。
表示平均收入。
例1.20
设某产品的价格与销售量的关系为
p
=
 ,求销售量为30件时的总收入与平均收入。
,求销售量为30件时的总收入与平均收入。
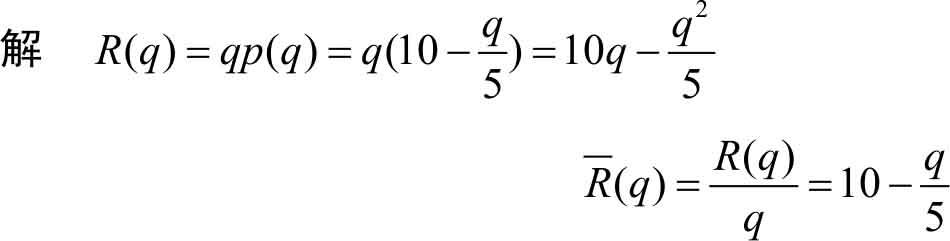
当 q =30时,总收入为
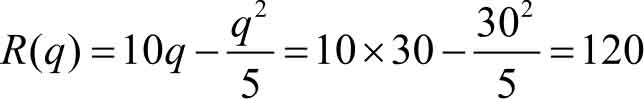
平均收入为
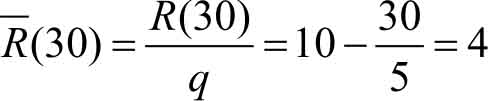
3.总利润函数
总利润 等于总收入与总成本之差。于是总利润函数为
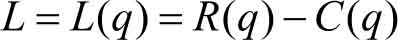
其中, L 表示总利润。
例1.21 某厂生产某种产品,每吨售价2万元,若每月生产 Q (吨)的总成本为 C (万元),且有 C = Q 2 -4 Q +5
(1) 写出总利润函数;
(2) 求出生产该产品的盈亏两平点。
解 (1) 由题意可知:总收入函数为
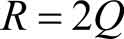
总成本函数为
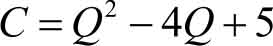
所以,总利润函数为
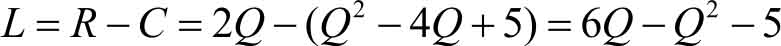
(2) 当总收入 R 与总成本 C 相等时,该企业既不盈利也不亏损。
又因为 R = C ,所以2 Q = Q 2 -4 Q +5,得 Q 2 -6 Q +5=0。
解得 Q 1 =1, Q 2 =5。
故该产品的盈亏两平点有两个,分别是生产1吨和生产5吨。作图,由图1-26可以看出,在区间(1,5)内总收入曲线在总成本曲线之上,它表示在区间(1,5)内每一产量 Q 都能使该工厂盈利,而区间(1,5)左右两侧的每一产量 Q 都能使该工厂亏损。因此,盈亏两平点 Q 1 =1是该工厂由亏损到盈利的转折点;盈亏点 Q 2 =5是该工厂由盈利到亏损的转折点。
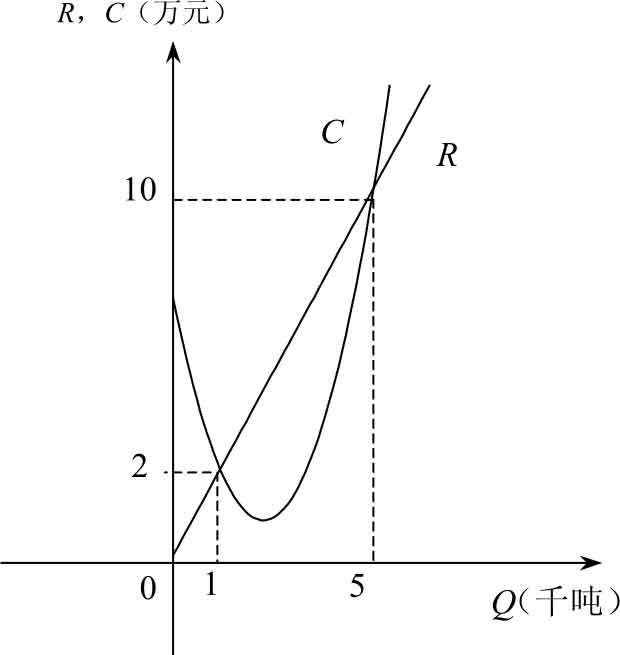
图1-26
习题1.5
1.设某商品的销售收入 R 是销售量 q 的二次函数,已知 q =0,2,4时,相应的 R =0,6,8。试确定 R 与 q 的函数关系。
2.某服装厂每月生产500套服装,定价为110元/套,当售出量不超过200套时,按照原价出售;售出量小于等于300套时,其中超过200套的部分,每套九折;售出量超过300套时,超过部分每套八折,试写出销售额与销售量的函数关系。
3.某玩具厂生产一件玩具的可变成本为18元,每天的固定成本为2 100元,如果每件玩具的出厂价为25元,为了不亏本,该厂每天至少应生产多少件玩具?
4.已知需求函数为 Q =100-5 p ,供给函数 S =-60+11 p ,求市场的均衡价格。


