
|
第七节
|
一、交流电与直流电有什么不同
(1)交流电 电流电压的大小和方向都随时间按一定规律(频率)交替变换, 比如50Hz就是它的频率,1s内大小和方向变换50次。电压有时为220V,有是为0V,有时为-220V。平时所说的220V指的是电压有效值。普通应用的交流电是按正弦函数规律变化的,也有非正弦交流电。
(2)直流电 电流电压方向一致,不随时间的变化而变化,并有“+”、“-”极之分。 但直流电的电压和电流也有变动,比如二极管整流后在未滤波稳压之前,叫做脉动直流电,但直流电的方向永远一致,由正到负,如电池等。
交流电的优点主要表现在发电和配电方面: 利用电磁感应原理交流发电机可以很经济方便地把机械能(水流能、风能……)、化学能(石油、天然气……)等其他形式的能转化为电能,交流电源和交流变电站与同功率的直流电源和直流换流站相比,具有造价低廉等特点,交流电可以方便地通过变压器升压和降压,这给配送电能带来极大的方便,这是交流电与直流电相比所具有的独特优势。
直流电的优点主要在输电方面。
①输送相同功率时,直流输电所用线材仅为交流输电的1/2~2/3。直流输电采用两线制,或以大地或海水作回线,与采用三线制三相交流输电相比,在输电线载面积相同和电流密度相同的条件下,即使不考虑趋肤效应,也可以输送相同的电功率,而输电线和绝缘材料可节约1/3。
②在电缆输电线路中,直流输电线路没有电容电流产生,而交流输电线路存在电容电流,引起损耗。
③直流输电时,其两侧交流系统不需同步运行,而交流输电时必须同步运行。
④直流输电发生故障的损失比交流输电小,两个交流系统若用交流线路互连需要很多的技术条件必须一致(如相位、频率、初相角、电压等),而直流电只需要电压一致。
二、交流电的几个要素
(1)周期( T ) 交流电从“0”开始:0→正最大→0→负最大→0,完成上述的一个循环所用的时间称为交流电的周期。用字母“ T ”表示,单位为“s”,如图1-31所示。
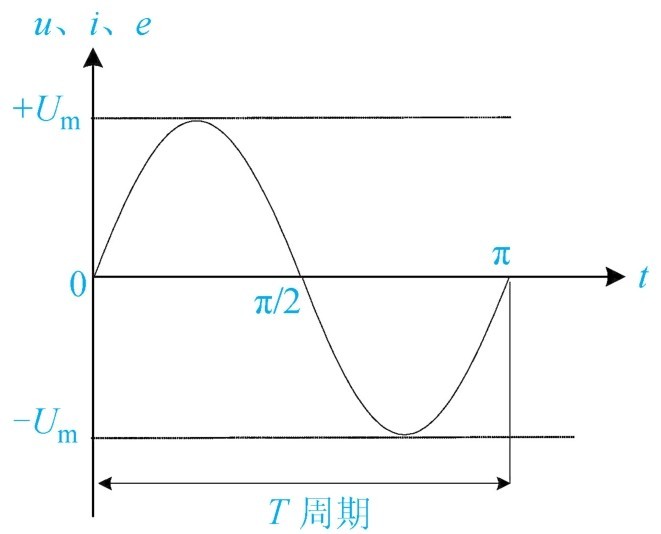
图1 - 31 周期的变化
(2)频率( f ) 正弦交流电每秒变化的次数,称为交流电的频率,用字母“ f ”表示,单位为“周/秒”或称为“赫兹”(Hz),如图1-32所示,一般50Hz、60Hz的交流电称为工频交流电。
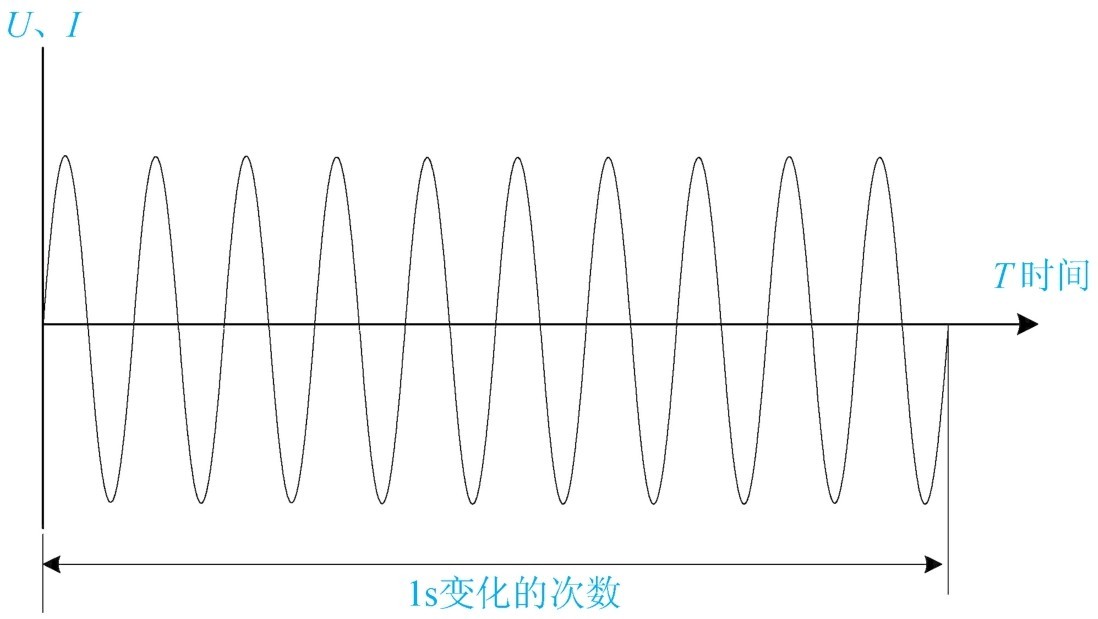
图1 - 32 频率的显示
频率和周期的关系是互为倒数: f =1/ T , T =1/ f 。
(3)瞬时值 正弦交流电在变化过程中,任一瞬时所对应的交流电的数值,称为交流电的瞬时值。用小写字母 e 、 i 、 u 等表示,如图1-33所示的 e 1 。
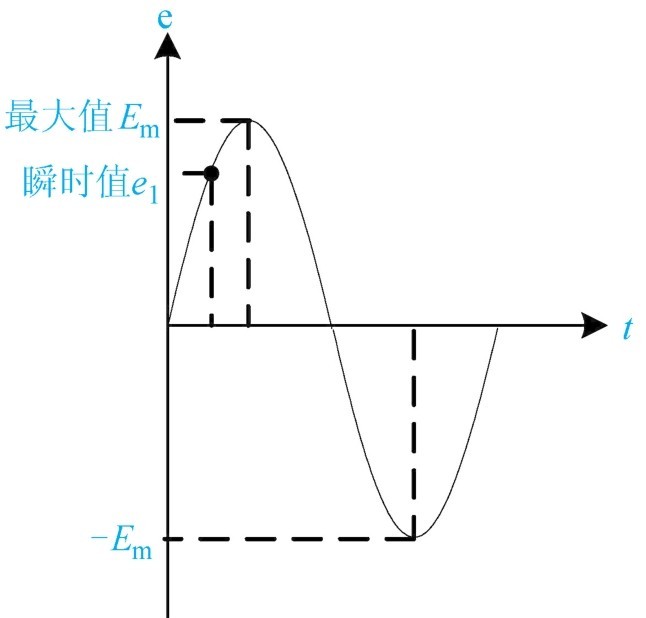
图1-33 最大值与瞬时值
瞬时值的函数表达式为: e = E m sin( ωt + φ )。
(4)最大值 正弦交流电变化一周中出现的最大瞬时值,称为最大值(也称为极大值、峰值、振幅值)。用字母 E m 、 U m 、 I m 表示,如图1-33所示的 E m 。
(5)有效值 当交流电流和直流电流,分别通过阻值相同的电阻,经过相同的时间、产生同样的热量时,把这个直流电流值叫做这个交流电流的有效值。用大写字母“ E 、 U 、 I ”表示。通常说交流电是220V、380V,就是指交流电的有效值为220V、380V。在实际工作中,如不特别指明均为电压的有效值。
有效值与最大值的关系为:最大值为有效值的
 倍,即:
倍,即:

(6)初相位 对正弦交流电开始时刻(常定为 t =0的时刻)已经变化过的角度(以小于360°)称为该正弦交流电的初相位。用字母“ ф ”表示,单位是“(°)”或“rad”。
初相位也可称作初相角。其值可能为零,也可能为正或为负,如图1-34所示。
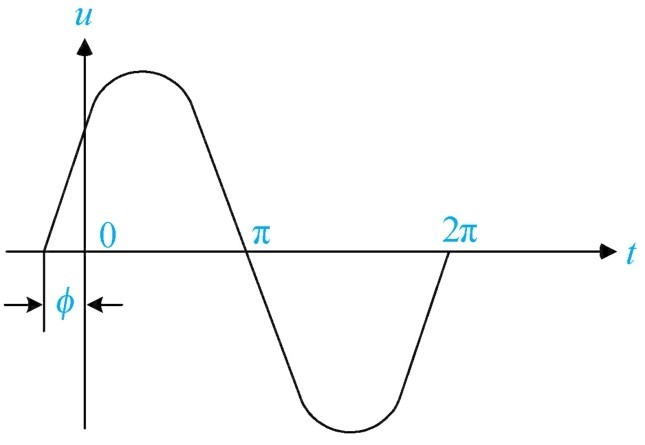
图1-34 初相角
(7)相位差 两个同频率正弦交流量之间的初相位之差,叫作相位差,如图1-35所示。
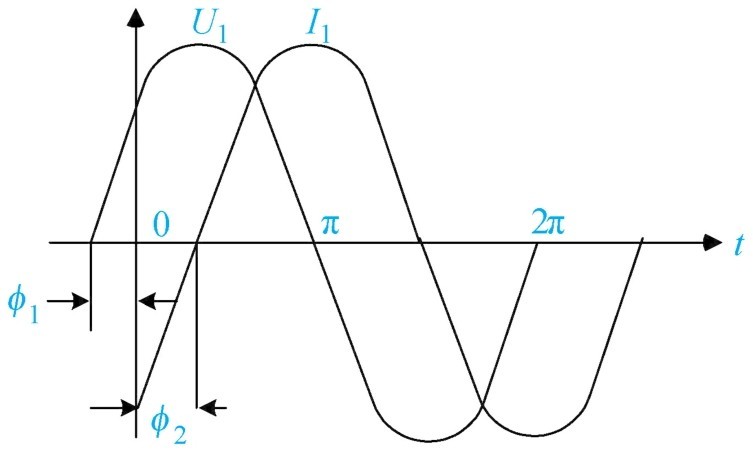
图1-35 相位差
例如: U 1 = U m sin( ωt + ф 1 ), I 1 = I m sin( ωt + ф 2 )。
则电压与电流之间相位差为:
ф 12 = ф - ф 2
相同频率的两个交流量在变化过程中,先达到最大值的一个量称作超前于另一个量。也可说后者滞后于前者。且习惯上超前或滞后的值以180°为限,否则将超前的值化作滞后的值。
两个同频交流量的相位差为零对,称作同相,相位差为18°时,称作反相。
三、三相交流电的定义
三相交流电源,是由三个频率相同、振幅相等、相位依次互差120°的交流电势组成的电源。如图1-36所示为三相交流电的波形。
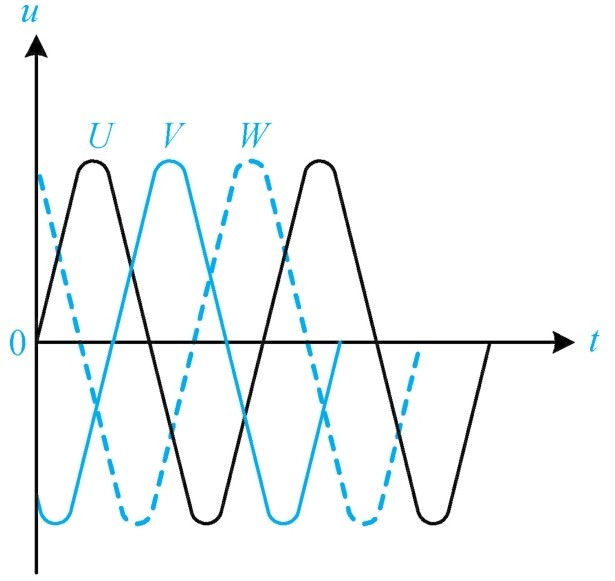
图1-36 三相交流电的波形
三相交流电较单相交流电有很多优点,它在发电、输配电以及电能转换为机械能方面都有明显的优越性。例如:制造三相发电机、变压器都较制造单相发电机、变压器省材料,而且构造简单、性能优良。又如,用同样材料所制造的三相电机,其容量比单相电机大50%;在输送同样功率的情况下,三相输电线较单相输电线可节省有色金属25%,而且电能损耗较单相输电时少。由于三相交流电具有上述优点,所以获得了广泛应用。
四、三相交流的相序
三相交流电动势在时间上出现最大值的先后次序称为相序。相序一般分为正相序、负相序、零相序。
最大值按 U → V → W → U 顺序循环出现的为正相序,如图1-37所示。最大值按 U → W → V → U 顺序循环出现的为负相序。
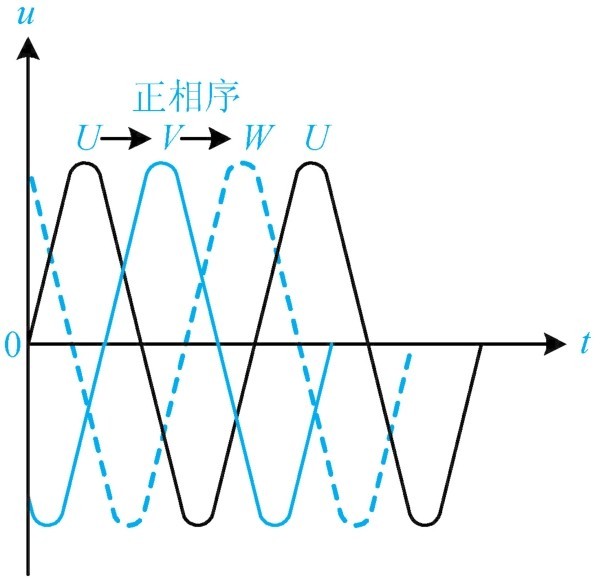
图1-37 正相序
五、三相连接电压、电流的关系
(1)星形连接电压、电流的关系 在生产中,三相交流发电机的三个绕组都是按一定规律连接起来向负载供电的。将电源三相绕组的末端 U 2 、 V 2 、 W 2 连接在一起,成为一个公共点(中性点),而由三个首端 U 1 、 V 1 、 W 1 分别引出三条导线向外供电的连接形式,称为星形(Y)连接,如图1-38所示。以这种连接形式向负载供电的方式称为三相三线制供电。这三条导线称为相线,分别用L 1 、L 2 、L 3 表示。在这三条相线中,任意两条相线间的电压称为线电压,用符号“ U L ”表示。
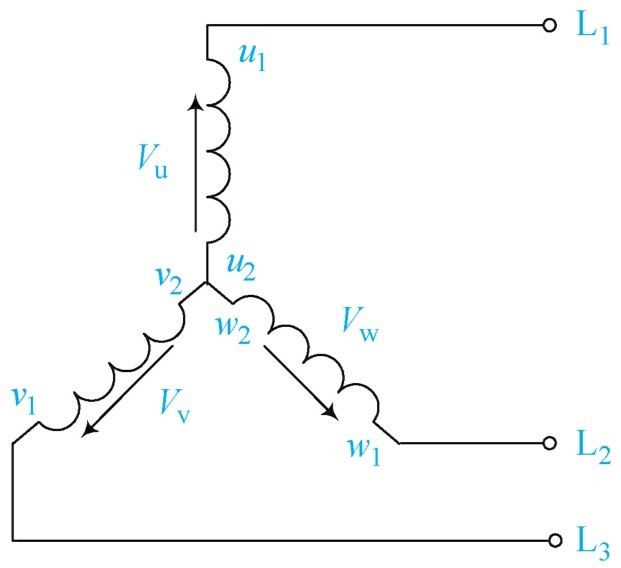
图1-38 三相三线星形连接
由中性点(已采取中性点工作接地的)引出的一条导线,称为零线,用字母“N”表示。
任一条相线与零线间的电压称为相电压,
用“
U
ф
”表示。这种以四条导线向负载供电的方式,称为三相四线制供电,如图1-39所示。三相四线制供电方式,可向负载提供两种电压,即相电压和线电压。相电流是指流过每一相电源绕组或每一相负载中的电流。用符号“
I
ф
”表示。任一条相线上的电流称为线电流,用“
I
L
”表示。在三相交流电的星形接法中,经数学推导可以证明,三相平衡时,
倍,线电流等于相电流。
即:电压关系为
U
L
=
 U
ф
、电流关系为
I
L
=
I
ф
。
U
ф
、电流关系为
I
L
=
I
ф
。
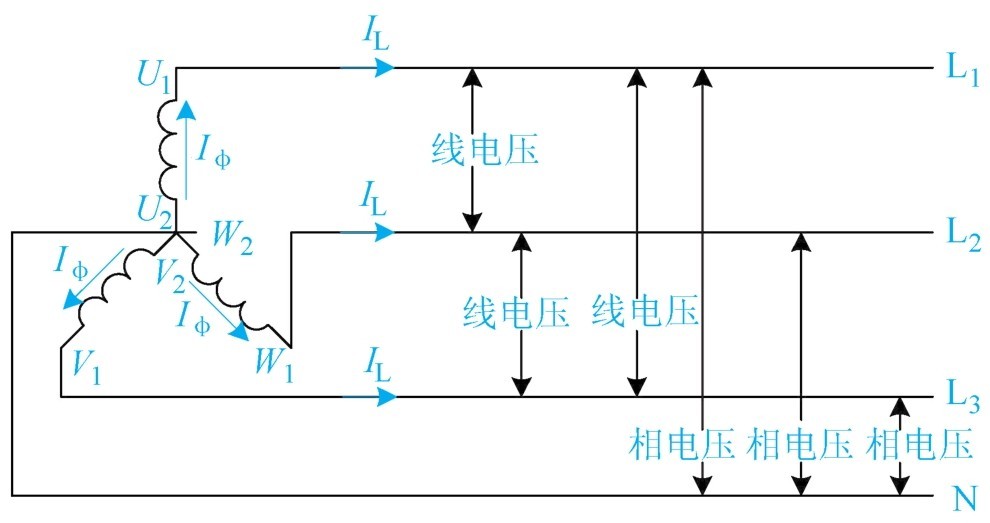
图1-39 三相四线星形连接
因此,220V/380V的三相四线制供电线路可以提供给电动机等三相负载用电,同时还可以供给照明等单相用电。
(2)三角形连接电压、电流的关系 将三相绕组的各相末端与相邻绕组的首端依次相连,即 U 2 与 V 1 、 V 2 与 W 1 、 W 2 与 U 1 相连,使三个绕组构成一个闭合的三角形回路,这种连接方式,称为三角形连接(△),如图1-40所示。
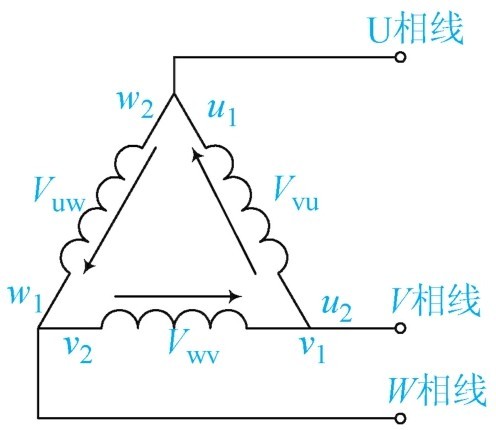
图1-40 三角形连接
三角形连接方法只能引出三条相线向负载供电。因其不存在中性点,故引不出零线(N线)。所以这种供电方式只能提供给电动机等三相负载的用电,或仅提供线电压的单相用电。
三角形连接的电压、电流关系如图1-41所示,线电压等于相电压;线电流等于
 倍相电流,
即:电压关系为
U
L
=
U
ф
、电流关系为
I
L
=
倍相电流,
即:电压关系为
U
L
=
U
ф
、电流关系为
I
L
=
 I
ф
。
I
ф
。
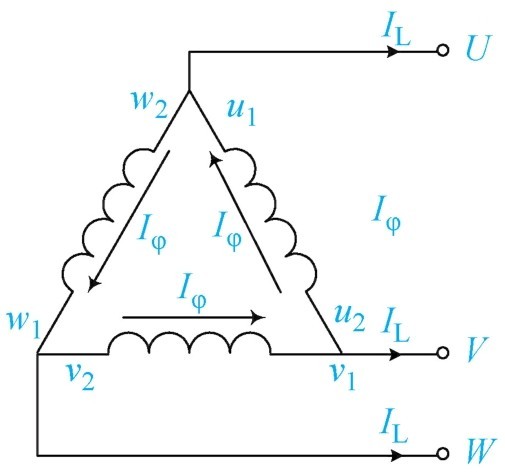
图1-41 三角形连接电压

六、三相负载的连接
(1)负载的星形连接 三相负载常采用星形连接或三角形连接的形式,如图1-42所示。对于低压较大容量的三相电动机,应采用三角形连接的方式。
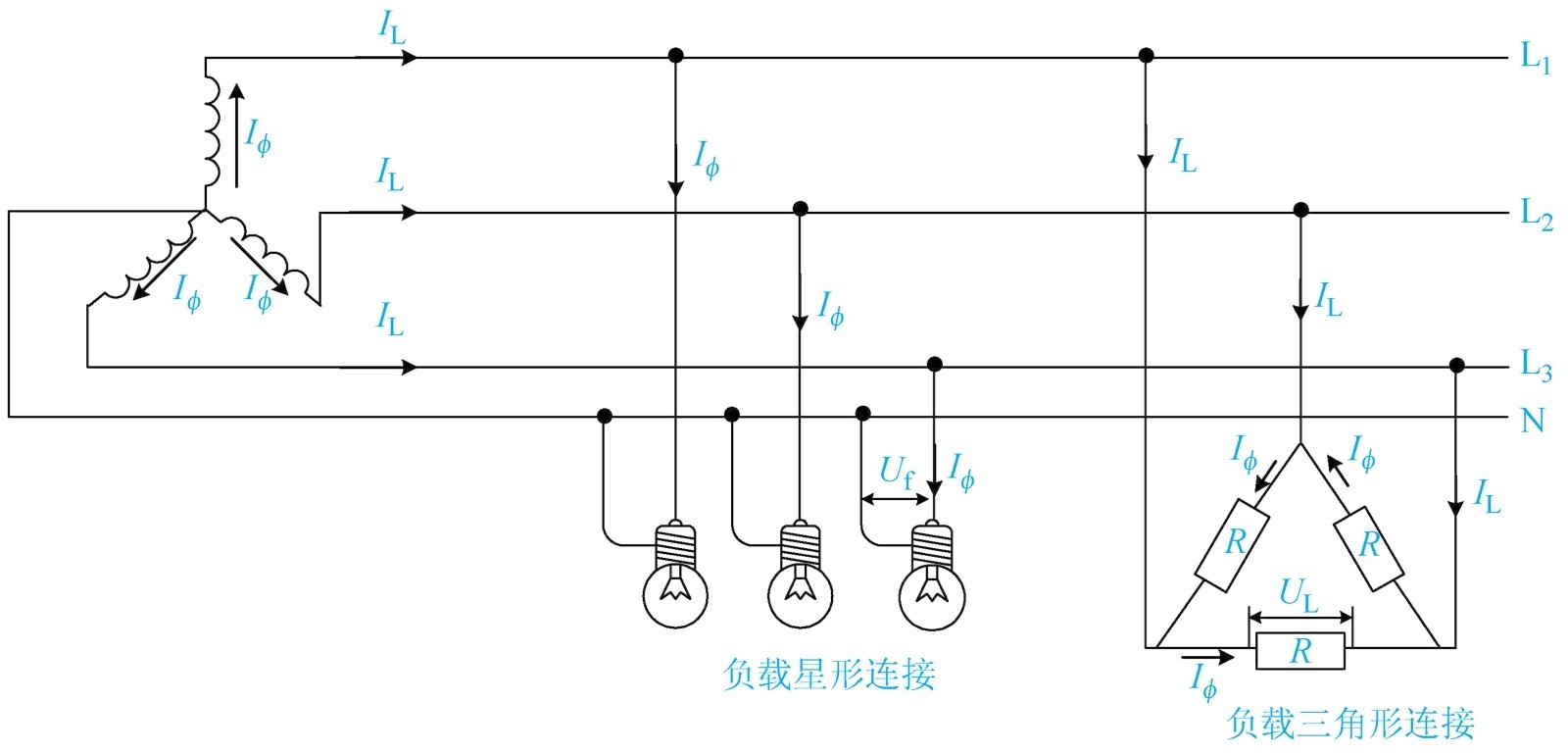
图1-42 负载星形的连接
三相负载星形连接:在星形连接的三相负载电路中,线电流等于相电流,这种关系对于对称星形和不对称星形电路都是成立的;如果是对称的三相负载,线电压等于相电压的3倍。
即:
U
L
=
 U
ф
,
I
L
=
I
ф
。
U
ф
,
I
L
=
I
ф
。
(2)负载的三角形连接
在三角形连接的三相负载。线电压等于相电压,无论三角形负载对称与否都成立。三相对称负载作三角形连接时,线电流等于相电流的3倍,即:
U
L
=
U
ф
,
I
L
=
 I
ф
I
ф
七、交流纯电阻电路特征与阻抗
在交流电路中只含有电阻用电器的电路,称为纯电阻电路。在实用中常常遇到纯电阻电路,如白炽灯、电炉子等。电路中电阻起决定性作用,电感和电容的影响可忽略不计的电路可视为纯电阻电路。这种电路的特点是电压和电流的初相角相同,如图1-43所示,所以电压和电流是同相的。在纯电阻电路中由于电阻是一个确定的值,所以电压与电流成正比,其有效值之间的关系为 I = U / R 。
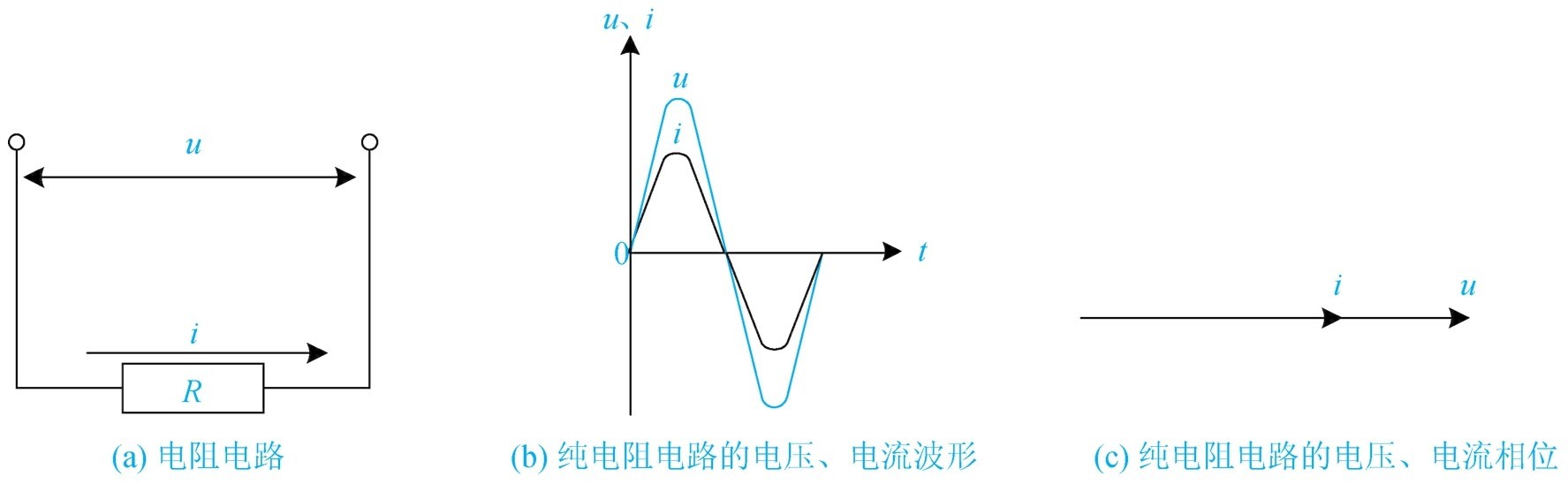
图1-43 纯电阻电路的电压、电流波形
由于电压和电流是同相的,则纯电阻电路消耗功率 P = I 2 R = U 2 / R
八、交流纯电感电路特征与感抗
(1)电感电路特征 电路中电感起决定性作用,而电阻和电容的影响则忽略不计的电路则视为纯电感电路,如图1-44(a)所示,在纯电感电路中,实际工作中的变压器、电动机就是电感类的设备,当电感类的设备通过交流电流时,由于电磁感应的存在,在电感线圈中就要产生自感电动势 e L ,这个自感电动势会阻碍线圈中的电流变化。这样, 使得电感上的电压超前于电流90° ,而电感上的电流又超前于自感电动势 e L 90°。因此, 自感电动势与电压反相。这种现象就可以解释在维修工作中用万用表测量线圈电阻只有几十欧姆,可是接到电源上时电流并不大,不符合电压除以电阻等于电流的公式,这就是自感电动势具有反抗电源电压的作用。
电感线圈上的电压、自感电动势、电流三者之间的相位关系可如图1-44(c)所示,电感线圈中的电流 i 和自感电动势的波形如图1-44(b)所示。
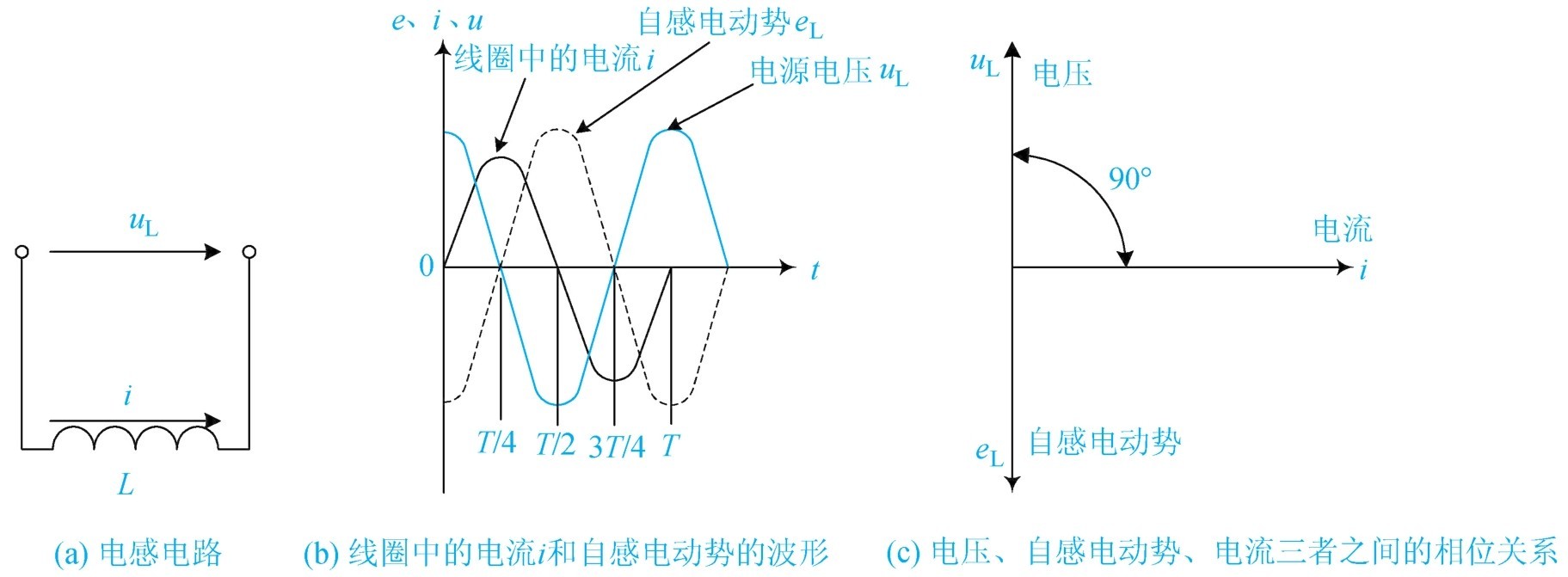
图1-44 电感电路及其电压、电流的曲线和相量
(2)感抗 交流电也可以通过线圈,但是线圈中的自感电动势对交流电有阻碍作用,如图1-45所示,这个阻碍就叫做感抗。电感量大,交流电难以通过线圈,说明电感量大,电感的阻碍作用大;交流电的频率高,也难以通过线圈,说明频率高,电感的阻碍作用也大。实验证明,感抗和电感成正比,和频率也成正比。如果感抗用 χ L 表示,电感用 L 表示,频率用 f 表示,则:
χ L =2π fL = ωL
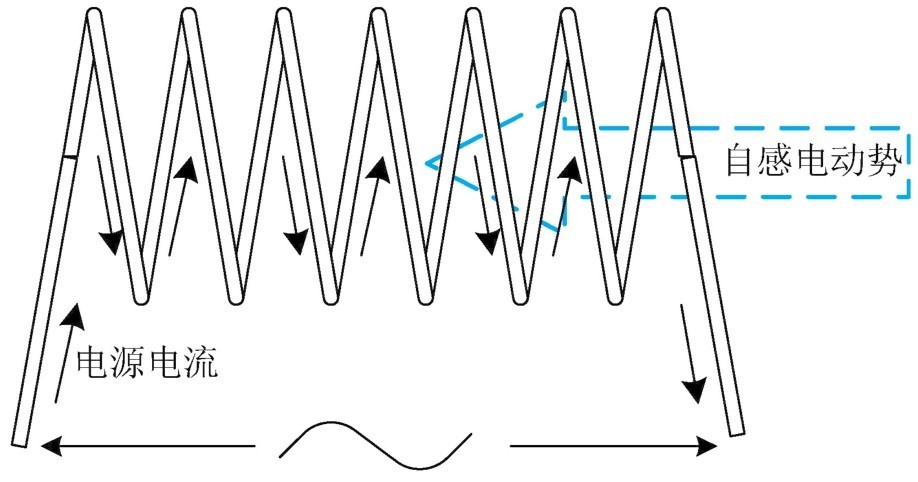
图1-45 感抗的方向
感抗的单位是Ω,知道了交流电的频率 f 和线圈的电感 L ,就可以用上式把感抗计算出来。
由于感抗与频率成正比,所以电感线圈对高频电流所呈现的阻力很大,频率极高时,电路中几乎没有电流通过,而直流电没有频率变化,稳定时不产生自感电动势。电路相当于短路,电流很大。在使用电抗器、接触器等有电感线圈的设备时,应特别注意这一点。
九、交流纯电容电路特征与容抗
由纯电容组成的电路应用十分广泛,在电力系统中常用来调整电压、改善功率系数等。
交流电流能使电容器两极间电压的大小和方向都随时间做周期性变化,当电压增大时,导体中的电流流向电容器,给电容器充电,在电路中形成充电电流;当电压减小时,电容器放电,电流流出电容器,在电路中形成放电电流。所以,尽管自由电子不能通过电容器两极间的绝缘介质,但在周期性交变电压作用下,电容器不断充电、放电,电路中就会形成持续的交变电流。
通过电容器电流的大小与电压变化率成正比。在电容器两端加一个正弦交流电压,如图1-46(a)所示。通过对如图1-46(b)所示的电压、电流曲线图的分析可以得知,电压与电流之间存在着相位差,即通过电容器的电流超前于电容器两端电压90°,它们的相量图如图1-46(c)所示。同时得知电容器上电流变化的规律及频率与电压相同,均为正弦波。
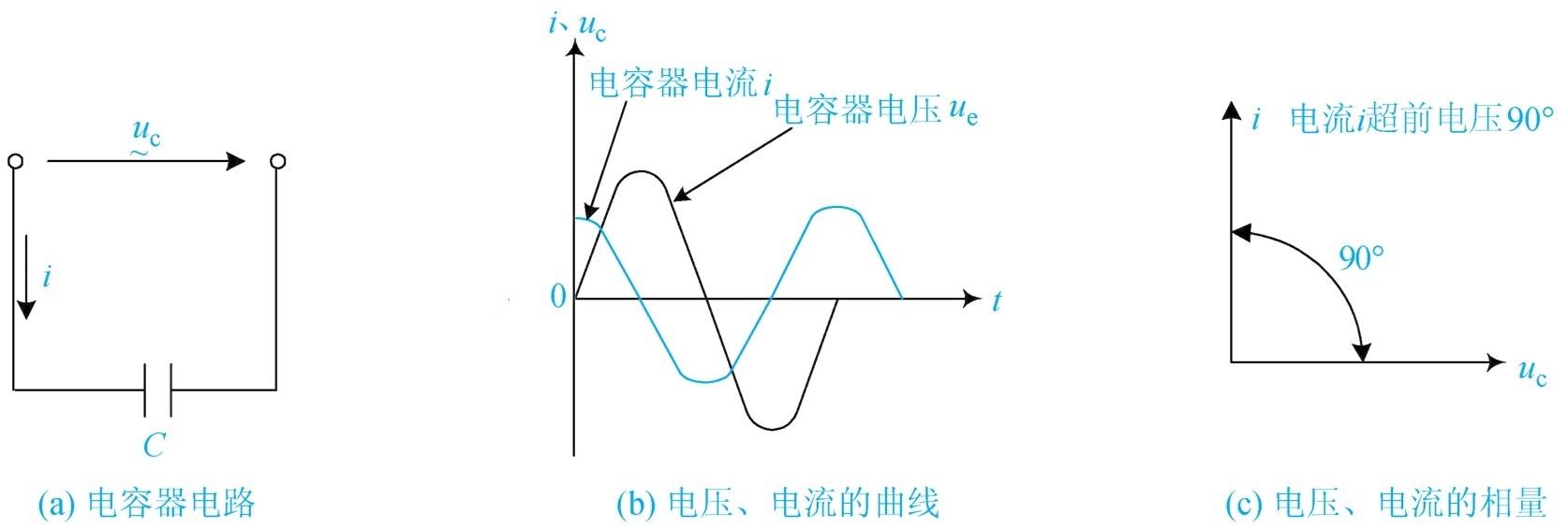
图1-46 电容电路及其电压、电流的曲线图和相量图
电容器对交流电也有阻碍作用,这种阻碍作用叫做容抗。容抗用符号“ χ C ”表示,单位是欧姆。其表达式为:
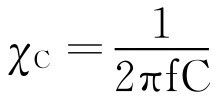
从公式中可以分析出容抗的大小与电容器本身的电容量、交变电流的频率有关:电容量越大、交变电流的频率越高,容抗就越小,电容器对交流的阻碍作用也就越小;反之,电容量越小、交变电流的频率越低,容抗就越大,电容器对交流的阻碍作用也就越大。当频率等于零时,容抗χ L 无穷大,所以电容有隔离直流、通交流的特性。
十、电阻与电容 R-C 串联电路
R-C串联电路是指电路中电感特性可忽略不计,电阻、电容特性起主导作用的串联电路,简称R-C串联电路。这种电路在电子技术中应用极为广泛,如阻容耦合放大器、R-C正弦振荡器等。其电路如图1-47(a)所示。
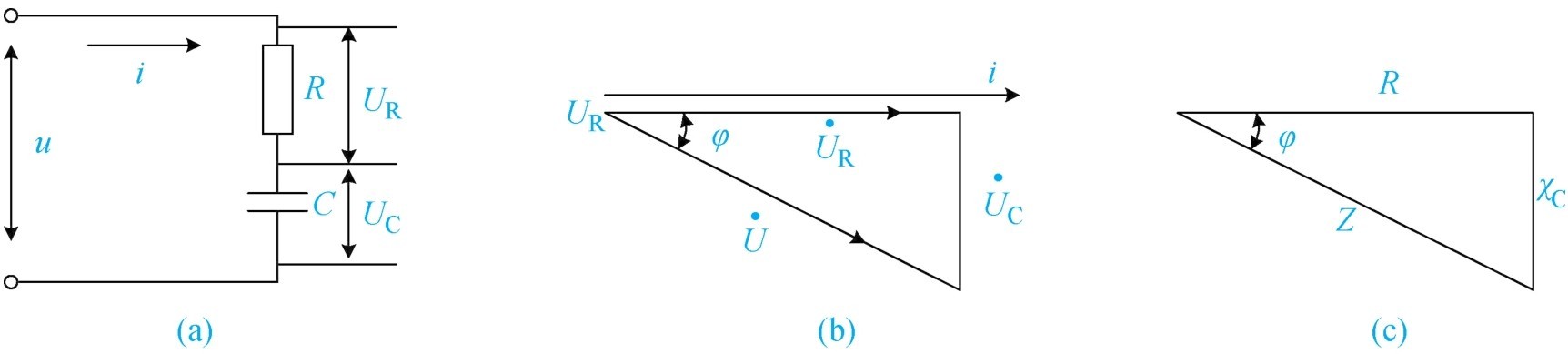
图1-47 R-C 串联电路的特征
在 R-C 串联电路中,流过电阻及电容器的为同一电流,且电阻两端电压与电流同相,但电容器两端电压滞后于电流90°,如图1-47(b)所示。
R-C 串联电路实验如图1-48所示;100V交流电、白炽灯60W、电容20μF,接通电源后灯泡稍亮。读取电表的数值发现, U =100V、 U 1 =80V、 U 2 =60V、 I =0.4A。
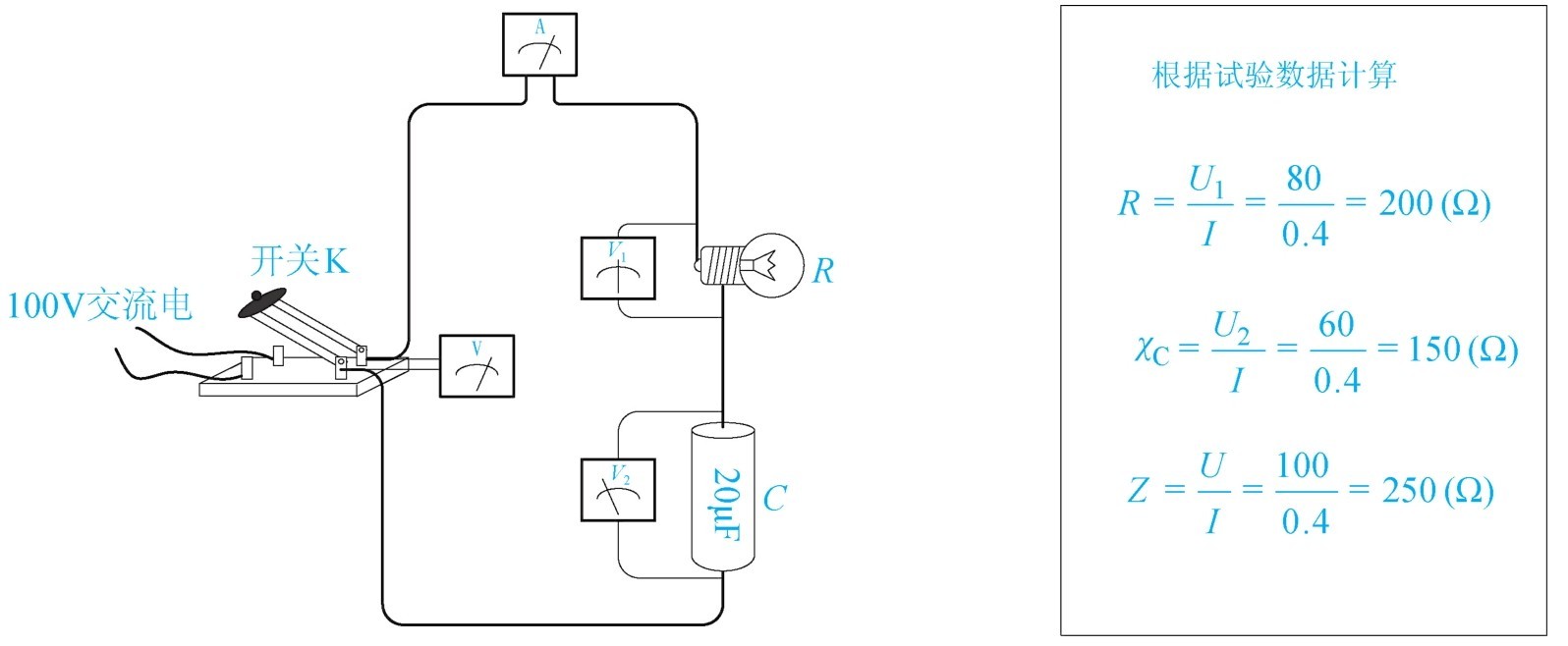
图1-48 R-C 串联电路实验
U 1 =80V, U 2 =60V,它们相加应等于140V,比电源电压100V高,这是由于电容两端的电压滞后电流90°,不能用加法直接计算,应该使用三角公式计算。
计算方法:

十一、电阻与电感 R-L 串联电路
这种电路是指电容特性可忽略不计,而电阻、电感特性起主导作用的串联电路,简称 R-L 串联电路。如日光灯、电动机、变压器等都可以看作为 R-L 串联电路。其电路如图1-49(a)所示。
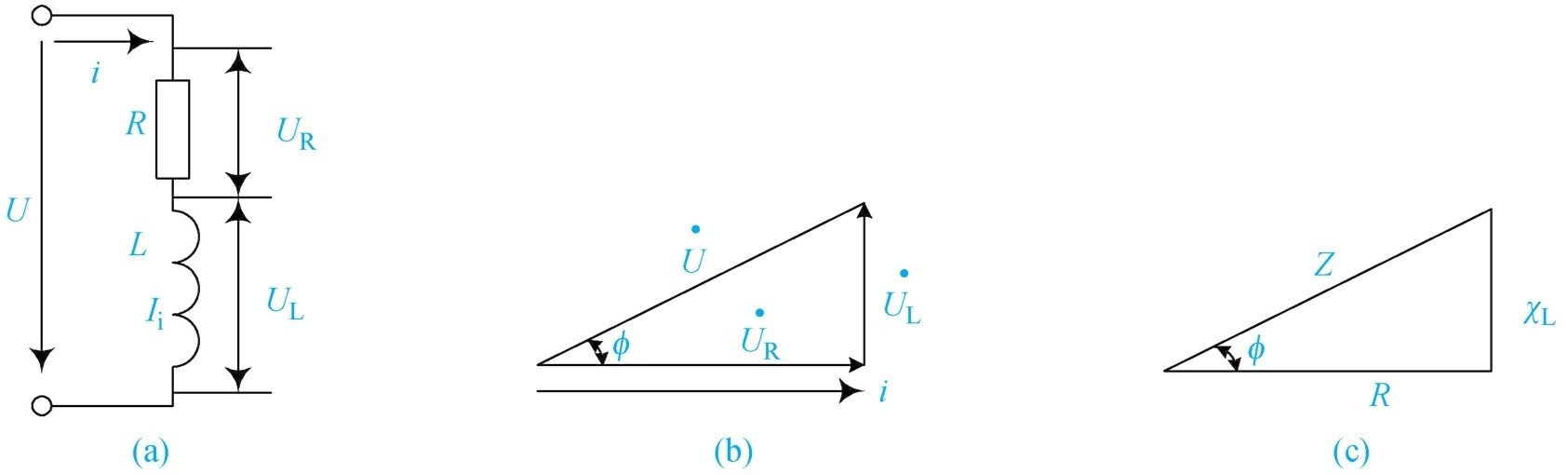
图1-49 R-L 串联电路特征
R-L 串联电路中,流过电阻和流过电感的为同一电流,但电阻两端电压与电流同相,电感两端电压超前于电流90°,见图1-49(b)所示。
R-L 串联电路实验如图1-50所示,100V交流电、白炽灯60W、电感线圈用变压器,接通电源后灯泡稍亮。读取电表的数值发现, U =100V、 U 1 =60V、 U 2 =80V、 I =0.2A。
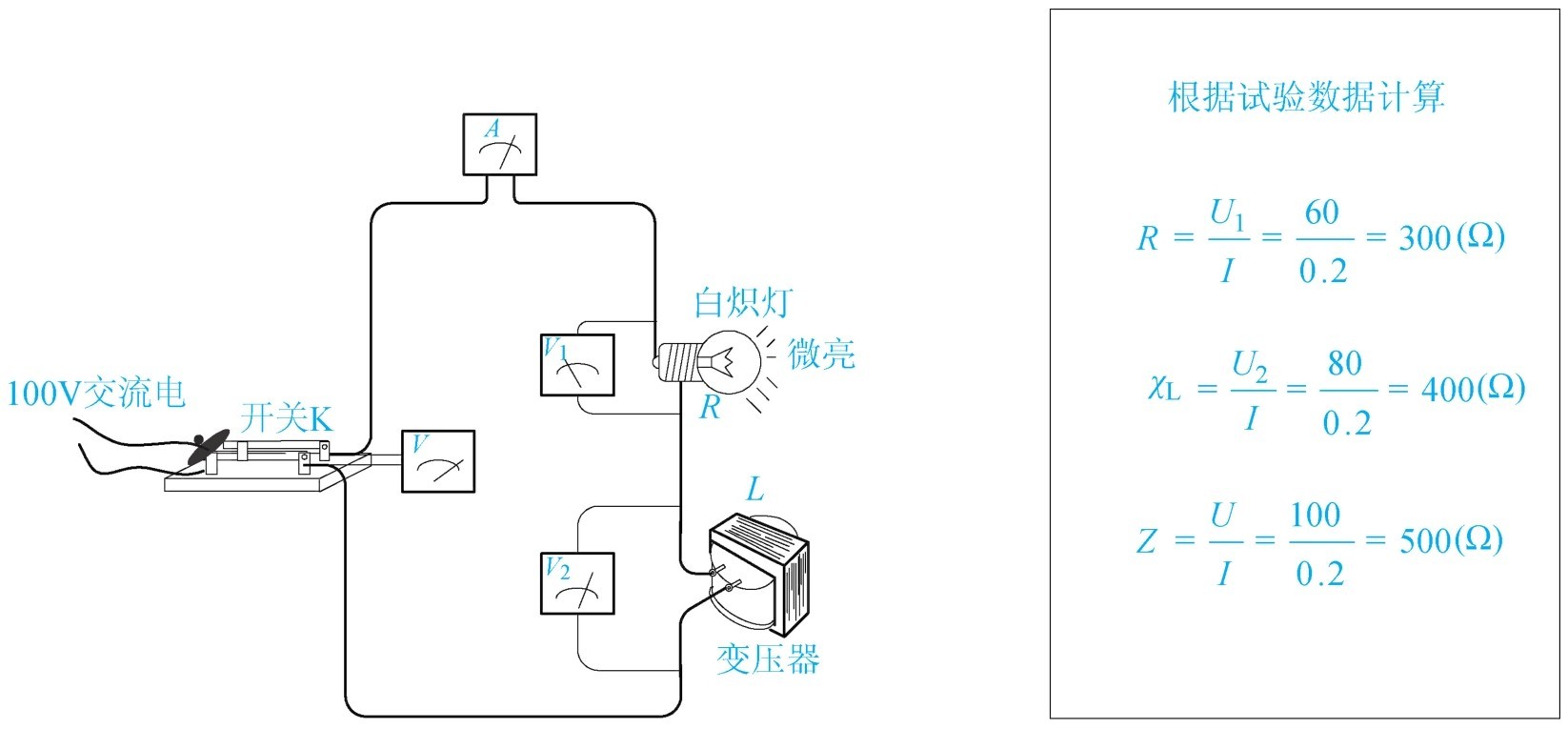
图1-50 R-L 串联电路实验
U 1 =60V, U 2 =80V,它们相加应等于140V,与电源电压100V不相符,这是由于电感两端的电压超前电流90°,不能用加法直接计算,应该使用三角公式计算。计算方法:
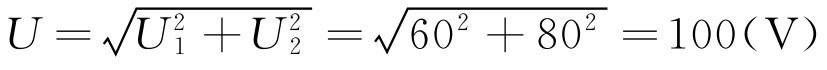
十二、电阻、电感与电容 R-L-C 串联电路
首先做一个实验,按如图1-51所示,将电阻元件灯泡、电感元件变压器和电容器串联接好,在电容器的两端接一个开关,接通开关K 2 ,在接通电源开关K 1 ,这时灯泡微微发亮,若打开K 2 开关,灯泡突然变亮。当开关K 2 合上时电容器短路,线路如同 R-L 串联电路,电流只有0.2A。打开K 2 开关,电容接入电路,这时灯泡变亮,说明电流增大,通过实验数据计算这时的电流为0.4A,电流变大。从前边的电感、电容介绍中可以知道,电感在交流电路中电流是滞后于电压90°的,电容在交流电路中是超前电压90°的,一个正、一个负两个相加就要相抵消掉一部分。
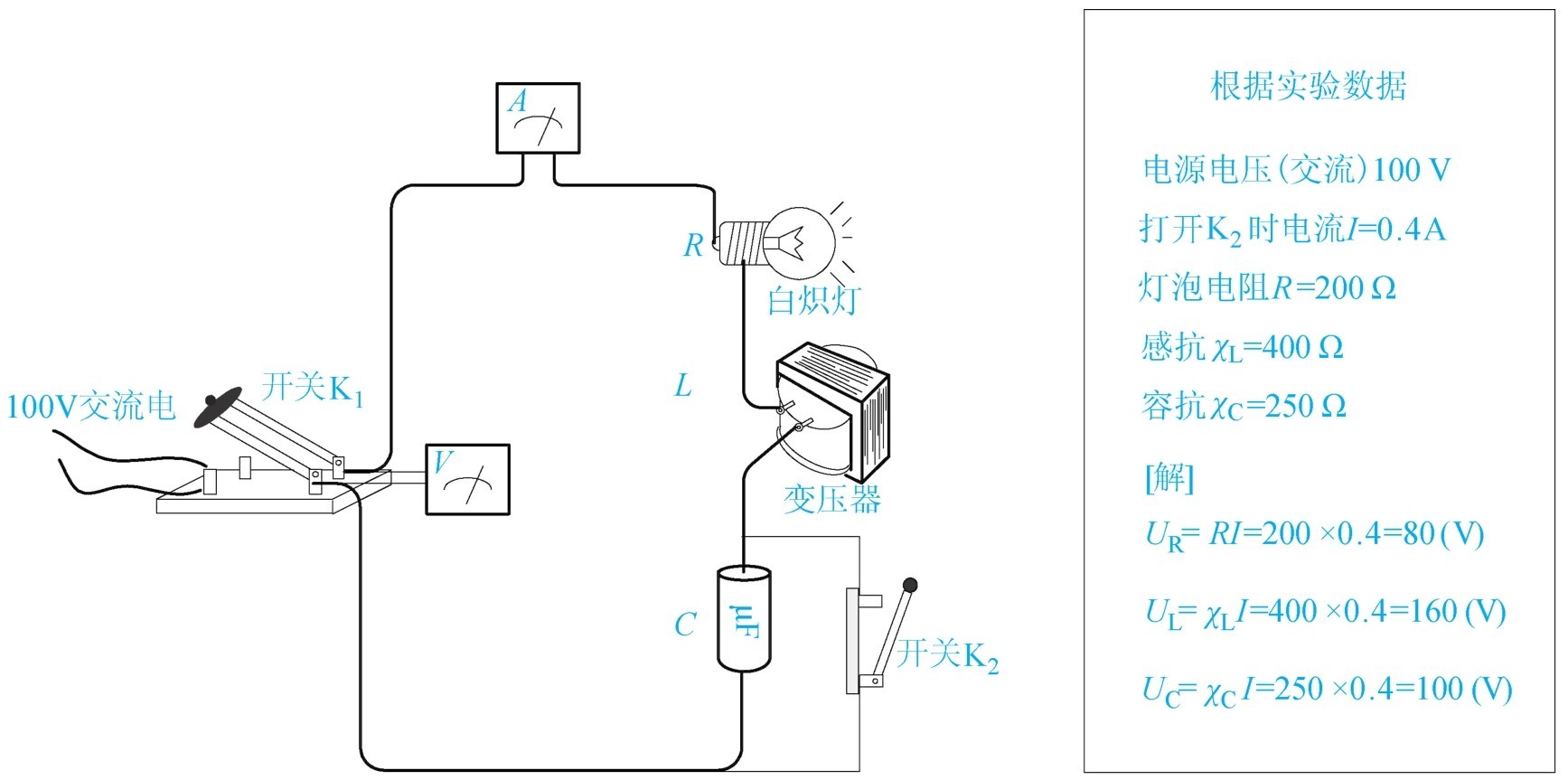
图1-51 R-L-C 串联电路实验
K
2
合上时线路的阻抗
 =447(Ω)100V/447Ω≈0.2A。
=447(Ω)100V/447Ω≈0.2A。
K
2
断开时线路的阻抗
 ,100V/250Ω=0.4A。
,100V/250Ω=0.4A。
当感抗大于容抗时,总的电抗电压超前于电流90°,总电压也超前于电流,这样电感的作用大于电容的作用,所以电路为电感性电路。
当感抗小于容抗时,电抗电压滞后于电流90°,总电压也滞后于电流,电容的作用大于电感的作用,电路为电容性电路。
当 χ L = χ C 时,这时总电压与电流同相,电路中呈现电阻性,这种情况称为谐振。因各元件是串联的,所以称为串联谐振。串联谐振也称为电压谐振。收音机的输入调谐回路就是利用调节可变电容器 C ,使回路对某一频率产生谐振。其特点是,电感或电容两端电压大于电源电压。
十三、电阻、电感与电容 R-L-C 并联电路
在家中使用白炽灯电流和电热器电流相加的总电流与配电盘的电流大小相同,若加上洗衣机和电冰箱的电流,发现不等于总配电盘的电流,这是为什么?
这是因为灯泡和电热器都是电阻负载,因此,流过的电流和电压同相位,而洗衣机和电冰箱的电动机是电感负载,流过的电流滞后与电压,这样不同相位的电流不能用普通的计算方法计算。
如图1-52所示是一个有趣的实验,先合上开关K 1 ,灯泡接通电流 I R =1A、 I N =1A;再合上开关K 2 ,变压器通电,变压器电流 I L =0.5A、 I N =1.1A;最后合上电容器开关K 3 ,电容器并入电路,电容器电流为1.25A,可这时总电流 I N 只等于1.25A。要使用代数和计算 I N = I R + I L + I C =2.75A,这是为什么呢?
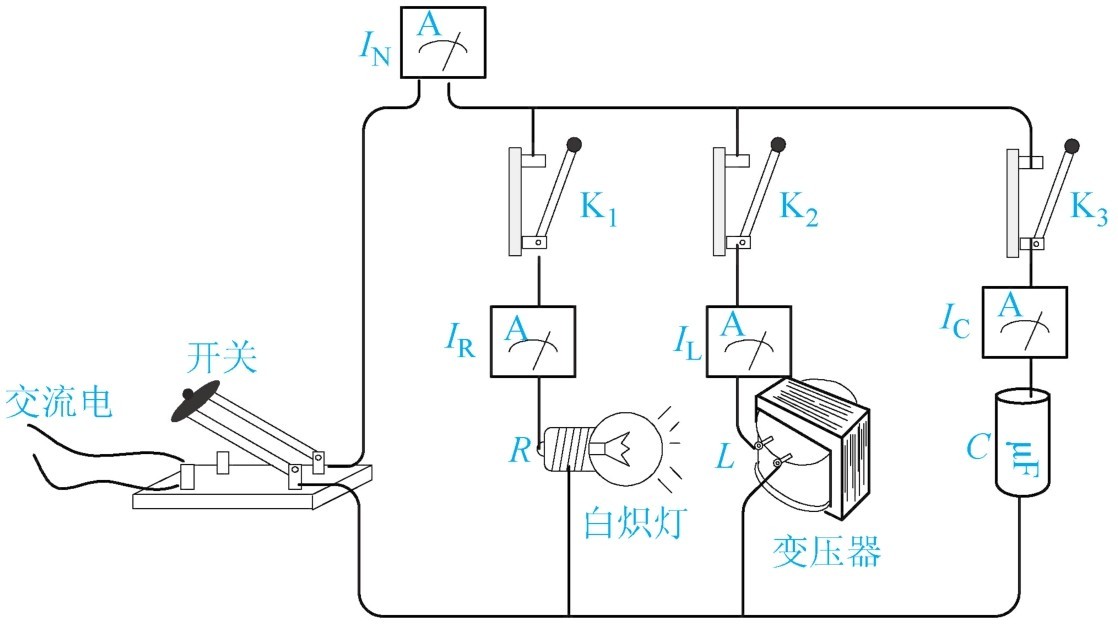
图1-52 R-L-C 并联电路
因为变压器和电容器的电流是矢量,不能直接用加法计算,要用矢量计算,也就是三角形计算方法,所以总电流的大小为
 =1.25(A)。
=1.25(A)。
这种电路是在工作经常遇到的。如为了提高电力系统的功率系数,常在负载端并联电容器,叫做并联补偿。
当 R-L 支路中的 I L > I C 时,总负载为感性的。
当 R-L 支路中的 I L < I C 时,总负载为容性的。
当 R-L 支路中的 I L = I C 时,则总电流和电压同相,这时电路的状态为并联谐振或称为电流谐振。
十四、利用三角形计算各种电量
在前面介绍交流电中各种的现象,当需要计算各种电量时,用普通数学方法计算出来的结果与实际不一样,这是因为在交流电路中各种电量的相位不同,所产生的和也不同,如图1-53所示如同两个人拉辆车,两个人方向一致时力量最大,如果两个人是朝两个方向用力那么就大打折扣。
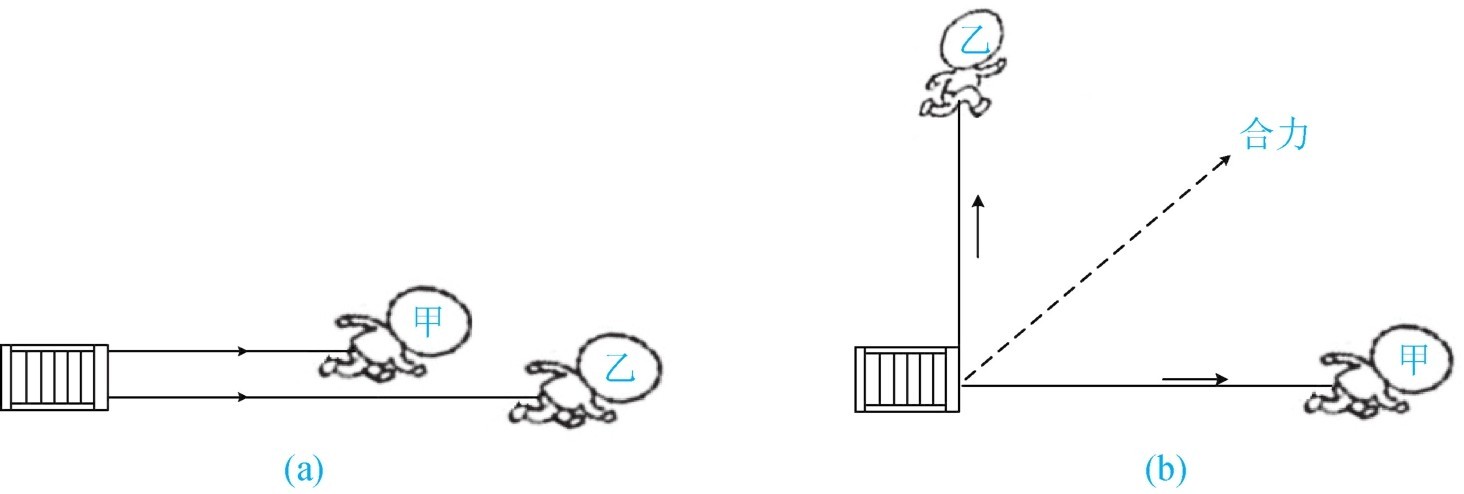
图1-53 相位相同合力最大
在电工的实践中利用勾股定理是最方便的一种计算方法,可以求出直角三角形的各个边长,如图1-54所示。

图1-54 勾股定理各边的关系
即;c 2 =a 2 +b 2
(1)阻抗三角形 如图1-55所示,阻抗三角形可以计算交流电路中电阻与感抗的关系。
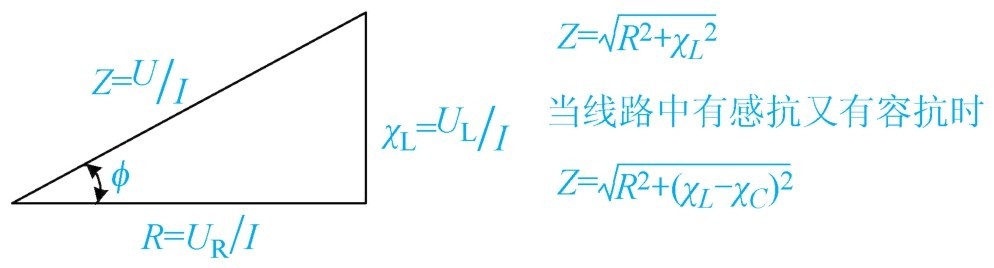
图1-55 阻抗三角形
Z 为线路阻抗(Ω); R 为线路电阻(Ω); χ L 为线路感抗(Ω)
(2)功率三角形 如图1-56所示,功率三角形可以分析交流电路中有功功率( P )、无功功率( Q )、视在功率( S )之间关系。
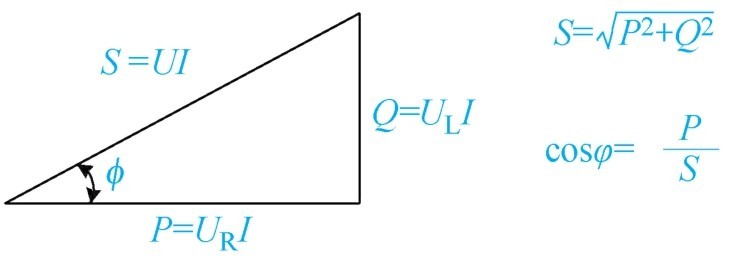
图1-56 功率三角形
S 为视在功率(kVA); P 为有功功率(kW);Q为无功功率(kVar)
(3)电压三角形 如图1-57所示,电压三角形可以分析交流电路中电阻、电感线圈上的电压。
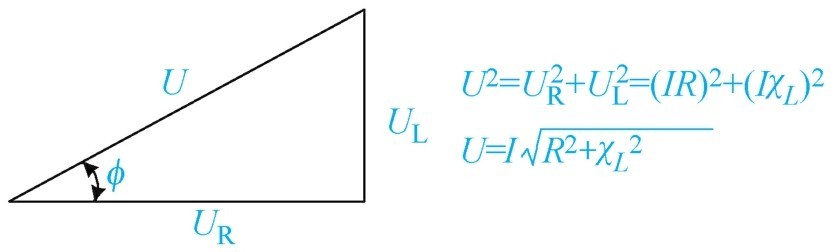
图1-57 电压三角形
(4)电流三角形 如图1-58所示,电流三角形可以计算交流电路中既有电感元件(无功电流 I Q )又有电阻元件(有功电流 I P )的工作总电流。
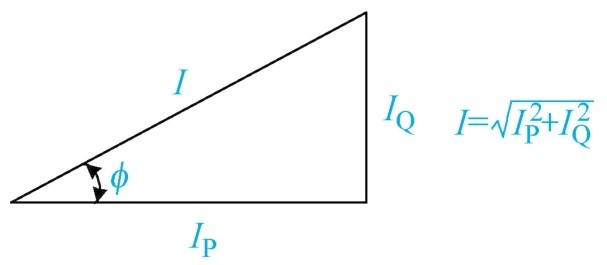
图1-58 电流三角形
(5)功率系数 功率系数是反映供电系统运行效率的一种比率。功率系数的大小与电路的负荷性质有关,如白炽灯泡、电阻炉等电阻负荷的功率系数为1,一般具有电感或电容性负载的电路功率系数都小于1。功率系数是电力系统的一个重要的技术数据。功率系数是衡量电气设备效率高低的一个尺度。功率系数低,说明电路用于交变磁场转换的无功功率大,从而降低了设备的利用率,增加了线路供电损失。
例如:某设备功率为100个单位,也就是说,要有100个单位的功率输送到设备中。然而大部分电器系统存在固有的无功损耗,只能使用70个单位的功率。虽然仅仅使用70个单位,却要付100个单位的费用,在这个例子中,功率系数就是0.7。这种无功损耗主要存在于电动机、变压器等设备中,又叫感性负载。
在交流电路中,电压与电流之间的相位差( ф )的余弦叫做功率系数,用符号cos ф 表示,在数值上,功率系数是有功功率和视在功率的比值。即:cos ф = P / S ,也可用阻抗三角形求得,cos ф = Z / R 。


