2.1 氢化非晶硅薄膜的特点

氢化非晶硅(Hydrogenated amorphous Silicon,a-Si:H)是在20世纪70年代研究发现的一种具有应用潜力的电子材料,并很快作为半导体材料以大的开关比(接近10 6 )和低的源漏关态电流而广泛应用于薄膜晶体管中。虽然非晶的a-Si:H许多性质与单晶硅(Crystalline Silicon,c-Si)相似,但薄膜中存在的大量无序的氢键和悬挂键影响了其电子的能带结构和载流子的传输特性。
2.1.1 原子排列和电子的态密度
晶体材料结构的基本特点是原子在空间的排列具有周期性或平移对称性,即称为长程有序;非晶材料结构的基本特点是原子在空间的排列不具有周期性,但在近邻和次近邻等极小的范围内原子的相对位置有一定的规律,即具有长程无序但是短程有序的特点,如图2.1所示。
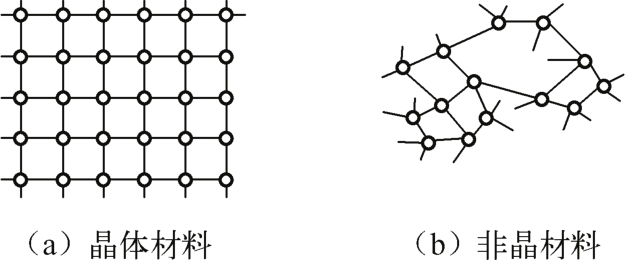
图2.1 晶体材料和非晶材料原子排布示意图
图2.2显示了晶态和非晶态半导体的电子态的导带、价带及各种缺陷产生的位于带隙中的局域态分布示意图。图2.2(a)所示为晶态半导体导带和价带的能态密度 g ( E ),两个能带中的状态均为扩展态, E C 和 E V 分别表示导带底和价带顶。图2.2(b)所示为价键饱和的理想非晶态半导体的 g ( E )模型。 E C 和 E V 分别表示导带和价带的迁移率边,此能量范围的电子状态都是局域态, E C 和 E V 间的能量间隙称为迁移率隙。带尾只占迁移率隙的一小部分, E A 和 E B 分别表示导带底和价带顶。带隙中的局域态形成有两种可能。第一种是非晶态硅中的断键,因为实际的非晶态硅中存在一定数量的断键,又称悬挂键,如同晶态半导体中的空位,这些悬挂键将在能隙中产生局域态。由于非晶态的结构无序,再加上悬挂键的数量比较多,这些局域态具有一定的态密度分布。
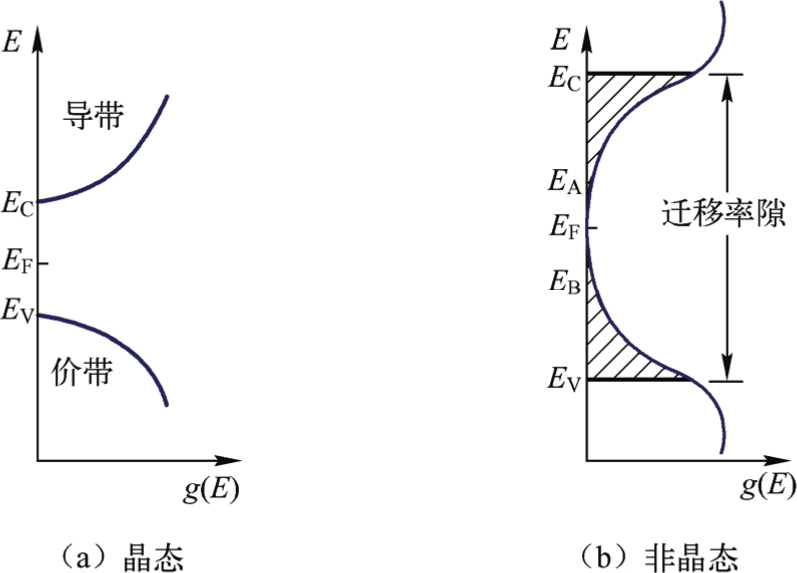
图2.2 晶态和非晶态半导体的能态密度分布模型
单晶硅具有标准的四面体的晶格结构,相邻原子间键长( a )为0.35nm,相应的键角为 109°。虽然氢化非晶硅材料具有很少或不具有长程有序,短程(约1nm)范围内仍保持硅晶格的四面体结构。因此,从微观上可以认为a-Si:H结晶网络是由和单晶硅中一样的Si—Si键构成的,但是在宏观上a-Si:H结晶网络又是无序的。即常用“无序度”表示a-Si:H结晶网络的无序性,并且以晶体的键长和键角的变化量Δ a 和Δ θ 来表示。对器件级的a-Si:H,发现键长变化量Δ a 约为晶体键长 a 的2%,键角变化量Δ θ 约为晶体键角 θ 的10%。
a-Si:H结晶网络的无序性意味着对于a-Si:H一个特定的键,键角和键长的偏移扰动着成键态的能量。c-Si导带和价带的边缘是清晰的;然而a-Si:H导带和价带的边缘有“带尾”(Band Tail),并扩展到迁移率隙(Mobility Gap)中形成指数形式减小的局域态(Localized State)。氢化非晶硅的电子态密度的能量分布如图2.3所示。随着键长和键角偏移的增加,某一特定的键会变得更弱,电子能级的扰动也将增加。因此,带尾可能与弱键(Weak Bond)有关,带尾的宽度成为晶体原子网络中无序程度的度量。带尾的宽度被称作Urbach能量(或Urbach斜率),可以用恒定光电流方法或光热偏移光谱仪实验方法进行测定。
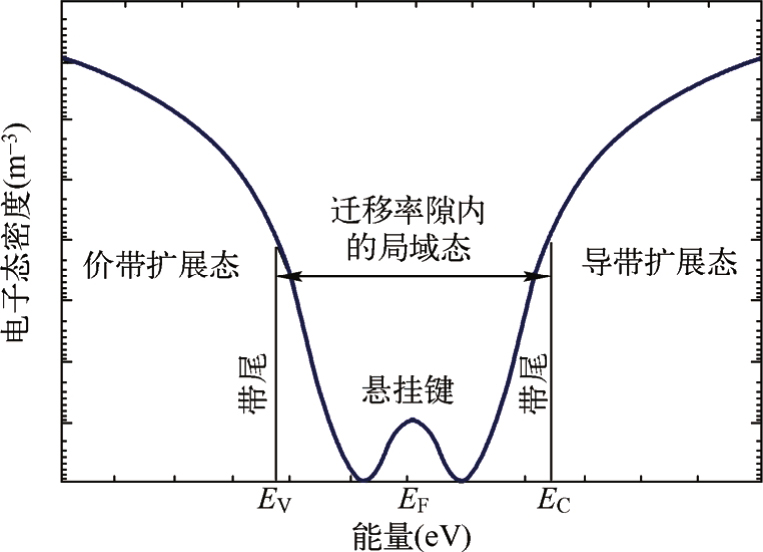
图2.3 氢化非晶硅的电子态密度的能量分布示意图
在氢化非晶硅中,如果特定的键发生高度畸变,则该键变得如此脆弱从而发生断裂,形成能量较低的两个“悬挂键”(Dangling Bond,D)。实际上,悬挂键的原本属性及其周边的环境将扰动它的能量。在图2.3 所示的电子能态密度分布图中,悬挂键分布于迁移率隙中心附近,即费米能级中心附近。那些分布于费米能级以下的悬挂键的能态表现为电子特性,通常用符号D - 表示;分布于费米能级附近的悬挂键不带电,用符号D 0 表示;分布于费米能级以上的悬挂键的能态表现为带正电,用符号D + 表示。在一特定的系统中,弱键和悬挂键之间存在一种平衡。当大量悬挂键被局域束缚,会使弱键分布变窄。因此带尾宽度和电子态密度分布中的悬挂键宽度有密切的关系。
未氢化的非晶硅(a-Si)内部有大量的悬挂键,缺陷密度达到10 26 m -3 。但是在掺氢之后,缺陷密度明显降低,悬挂键的缺陷密度低于10 22 m -3 ,即掺氢后的氢化非晶硅是一种高质量的半导体。氢钝化缺陷的机理是使悬挂键变成Si—H键。因此,由于a-Si:H薄膜中氢含量增加,悬挂键(带隙中间的缺陷态)的数量降低了,既释放了晶格网络中的局域应力,也降低了弱键的密度。换句话说就是以这种方式降低了带尾宽度,带隙变宽了。因此,带隙和氢含量之间有着密切的关系。氢原子能够在生长中的a-Si:H中扩散并且钝化缺陷。氢原子实际在弱的Si—Si键之间移动。氢从弱的Si—H键中脱离是受该键释放出氢原子所需能量大小的影响。所以,a-Si:H 中氢的扩散是一种热激活的过程,即与温度有关。因此薄膜的沉积温度是控制a-Si:H中氢含量的一个关键工艺参数。通常,薄膜沉积期间的衬底温度越高,所形成的a-Si:H的氢含量就越低,其光学带隙也越窄。
器件级的a-Si:H的氢含量一般约10%(由傅里叶变换红外光谱仪确定)。低于这个浓度,对于一个硅原子一般只有一个H原子成键。然而,事实上氢钝化悬挂键时,很难发现完全孤立存在的氢,而恰恰是两个氢原子紧密接近,每一个氢原子分别附加到一个硅原子之上,这两个硅原子有潜在形成一个弱键的可能性。其中一个氢原子位于两个硅原子间的“键中心位置”,由于空间的限制,另一个位于四面体格点附近的位置。这一双氢弱键组态有时标记为SiHHSi,被称为
 组态。有时一对悬挂键只有一个被氢原子钝化,产生一种SiHDSi组态。
组态。有时一对悬挂键只有一个被氢原子钝化,产生一种SiHDSi组态。
如果氢原子含量增加到10%以上,那么非晶硅就可能形成一种聚合材料,其中两个H原子结合到一个Si原子上。这个Si 原子只能与其他硅原子形成两个键,形成类似于在碳系统中的烷链状结构。氢含量的进一步增加可能使氢从硅网络中析出或氢原子聚集到一起形成微小空洞。此时薄膜的缺陷态密度升高,电学特性变差。
2.1.2 氢化非晶硅的导电机理
如2.1.1节所述,a-Si:H晶格结构具有三种类型的电子态:深入带隙内的悬挂键形成的缺陷态、位于带隙边缘的弱键形成的带尾态和四面体网格结构的导带与价带形成的扩展态。不同的载流子导电机理与这三种能态都有密切联系,哪一种占优势取决于费米能级的位置和温度,或者说就是这三种电子态的哪一种热激发产生了电子和/或空穴。为便于讨论,我们假设a-Si:H是本征的,费米能级靠近带隙正中间。
低温时,费米函数 f 变成以费米能级 E F 为中心的函数:
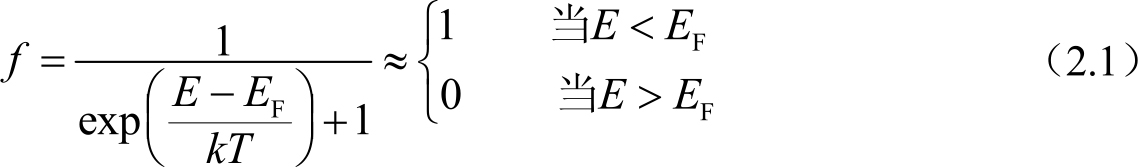
在晶体硅中,导带无多余的自由电子,价带无多余的自由空穴,因而晶体硅不会导电。但是,带隙中间的缺陷态的存在改变了这一点。占据费米能级下方局域悬挂键的缺陷态的电子可能刚好接近于费米能级上方未占据的局域缺陷态。在电场和/或几乎不高的热能作用下,电子可能由第一态隧穿到达第二态。假设费米能级附近能量范围内的缺陷态密度近似为常数,那么电导率可以由Mott提出的变程跃迁模型来描述,其中的跃迁电导率 σ h 与温度的关系为

式中, σ h0 是跃迁电导率前因子; a h 是一个常数。
低温时,电子被看作在迁移率带隙中的缺陷态对应的一系列势阱。当在一个称作可变程跃迁的过程中,在电场作用下,电子可以在围绕费米能级的这些态之间隧穿。随着温度升高,有足够的热能使一些电子激发到导带尾,而在价带尾留下空穴。电子在带尾定义为形成弱键。在电场作用下,电子(和空穴)可以由一个局域态隧穿到另一个局域态,这一过程称为带尾跃迁。电子或空穴占据这一态的几率由费米函数给出,在分布的尾部近似于玻尔兹曼分布:
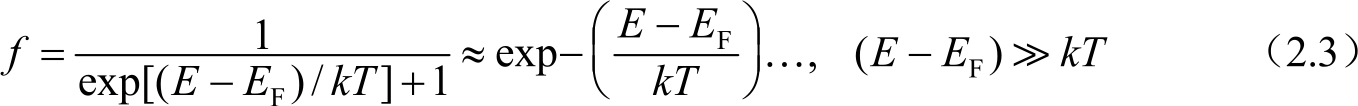
由于带尾跃迁电导 σ t 与有效载流子数量呈线性关系,所以它也与温度呈指数关系:
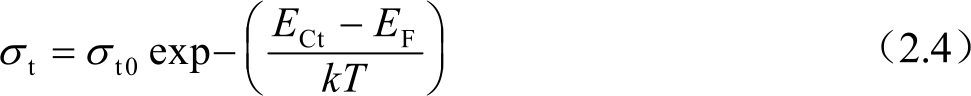
式中, E Ct 是导带尾态的平均能量。前因子 σ t 0 取决于跃迁的几率,也就是取决于带尾态密度和它们的波函数间的重叠量,通常测量值在10 -2 ~1Ω -1 m -1 。
当温度高于500K时,有足够的能量使a-Si:H系统中的电子和空穴从带尾分别激发到导带和价带中。此时载流子不受局域缺陷或弱键的限制,在扩展态中通过四面体硅结构的周期势垒自由地移动。由于非晶硅晶格中不存在长程有序,载流子发生频繁的散射,电子迁移率只有1cm 2 /V·s;空穴迁移率比这一迁移率低两个数量级。相比较,单晶硅的电子和空穴的迁移率分别是 1350cm 2 /V·s 和480cm 2 /V·s。扩展态的载流子数目遵循玻尔兹曼分布,式(2.3)的条件再一次得到满足,所以,扩展态电导率( σ e )与温度也是指数关系:

式中, E C 是导带底的能量,在非晶硅中也通常称作“迁移率边”,被定义为电子态密度图上的一个点,超过这一点的载流子处于扩展态。导带和价带迁移率边之间的能量差称作迁移率带隙(Mobility Gap)。由于这一导电机理不受遂穿势垒的限制,这样的电导前因子( σ e0 )比带尾跃迁式的要大得多,测量值约为10 4 Ω -1 m -1 。
室温下,这三种导电机理中起主导作用的是带尾跃迁式。所以,a-Si:H的电导率通常非常低(约10 -8 Ω -1 m -1 )。然而,当光子能量大于迁移率隙时,光照射a-Si:H 在扩展态产生电子空穴对,电导率急剧增加。具有少量的中间带隙缺陷态(它充当复合中心)的器件级a-Si:H,在光照射下的电导和暗电导比值(亦称为光敏性)能够大于10 6 。
对于a-Si:H TFT,施加正极性栅压将增加导带迁移率边以上的电子数目。这会引起费米能级移入导带尾中。因此,中间带隙缺陷态需要填充电子,变为D - 。这需要一定的电荷来填充,因此栅极需要施加比预期更大的电压。为了得到低阈值电压和高亚阈值斜率的TFT特性,就需要低缺陷态密度、低带尾态和工作期间最小缺陷产生率的氢化非晶硅。
以a-Si:H作为沟道层的TFT的应用领域受到一定局限性,是因为扩展态电导的低迁移率。缺陷和弱键的数量降低了载流子的迁移率,a-Si:H 中硅晶格的无序性本质上决定了使用该材料可以达到的电子和空穴迁移率的上限。TFT的开关速度与载流子的迁移率成正比,所以n型a-Si:H TFT的开关速度比同等的c-Si器件低1000倍。液晶显示中的像素TFT只有微秒级的开关时间,a-Si:H对这种应用是满足的,但是,液晶显示信号处理的视频解码电路需要快得多的开关速度,应用a-Si:H的器件就不能满足了。此外,低的空穴迁移率也阻碍了互补型(n和p型)氢化非晶硅器件的应用。因此,需要开发微晶硅(Micro-crystalline Silicon,μc-Si)或多晶硅(Poly-crystalline Silicon,p-Si)作为高速TFT的替代半导体材料。
2.1.3 氢化非晶硅的亚稳定性
a-Si:H晶格结构中存在Si—Si弱键、悬挂键和Si—H键之间的亚稳定平衡态,在外部能量作用下既可以改变这一平衡,也可以把它恢复到原平衡态。氢化非晶硅中的这种平衡态被称为亚稳定性。
a-Si:H亚稳定性存在的最著名的例子就是Staebler-Wronski效应。实验观察到光照射a-Si:H引起暗电导和光电导随着照射时间降低,随后在约200℃下退火几小时后又还原到原来的电导值。正因为这一原因,有源矩阵液晶显示器(Active Matrix Liquid Crystal Display,AMLCD)中的a-Si:H TFT需要有对背光源或环境光的遮蔽层。
另外一个实验也观测到了a-Si:H TFT的亚稳定性。当在a-Si:H TFT的栅极和源极间加以偏压,观察到阈值电压随时间而增加,一直达到栅偏压。其后在不加偏压情况下并在约 200℃进行几小时的退火,阈值电压又恢复到原值。尽管在AMLCD应用中,TFT晶体管驱动的栅压占空比低,TFT的亚稳定效应并没有成为其实际应用的障碍。但是如果应用于有机发光二极管(OLED)显示器件中,TFT被用于以电流形式驱动,且占空比高,则该效应就明显多了。
通常认为各种状况下a-Si:H的亚稳定退化作用都是由于悬挂键而引起的,并且在退火过程中氢钝化了这些悬挂键。这种亚稳定性可以用下述的可逆反应来描述:
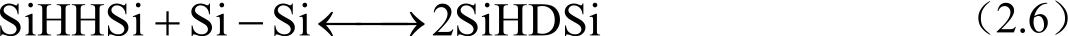
式中,由左边转化为右边代表性能退化,通过退火的逆过程代表还原。两种状态间的转化需要额外提供热激活能。
图2.4是通过激活能实现缺陷态产生和恢复的能量示意图。由于缺陷产生的速率不一定与缺陷恢复的速率相同,因此势垒高度取决于反应的方向。
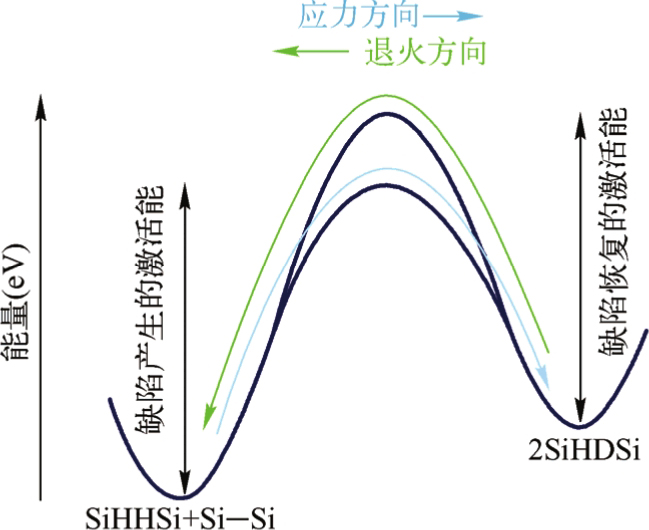
图2.4 通过激活能实现缺陷态产生和恢复的能量示意图
Wehrspohn 等人利用TFT进行了系统的研究,结果表明对于一给定的a-Si:H,有一个产生缺陷的激活能的分布。该分布的峰值能量表现出与a-Si:H本征薄膜压应力之间的明确关系,压应力与Si—Si键的能量有关。峰的宽度与带尾的宽度有关,而带尾宽度取决于Si—Si弱键的能量分布。短的Si—Si键是最弱的,所以缺陷的发生最可能归结为以下机理:外加能量使短的 Si—Si 弱键断裂形成两个悬挂键(SiDDSi),但是通常该键几乎可以马上恢复。然而,如果这个断裂的键位置靠近双氢硅键(SiHHSi)(很可能是
 组态),于是两个氢原子中的一个可以转化为一个硅原子以稳定两个悬挂键中的一个,留下两个SiHDSi缺陷态,如式(2.6)所示。
组态),于是两个氢原子中的一个可以转化为一个硅原子以稳定两个悬挂键中的一个,留下两个SiHDSi缺陷态,如式(2.6)所示。
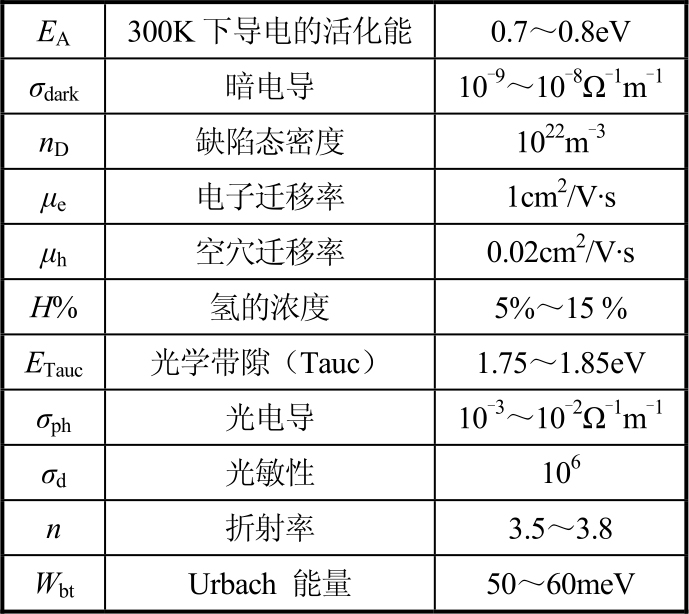
表2.1 用于AMLCD中的器件级a-Si:H薄膜的特点
在逆过程中,在退火条件下,H原子中的一个有足够的能量跃迁回到另一个SiHDSi键,从而再一次使其双氢化。两个悬挂键于是处于两个硅原子中间,然后可能重新恢复成一个Si—Si弱键,同时两个缺陷湮灭。缺陷恢复的激活能取决于破坏Si—H键所需要的能量。该过程的平均能量(1.3~1.5eV)高于缺陷产生的激活能量,而缺陷产生的激活能取决于更弱的Si—Si弱键的断裂能(约1.0eV)。
表2.1列出了典型的应用于AMLCD中的器件级a-Si:H薄膜的性质。


