3.5 像素设计原理

3.5.1 电容
1.液晶电容计算
液晶分子具有电学各向异性,即在长轴和短轴上的介电常数不一样。当长轴介电常数比短轴大时,被称为正性液晶,反之则被称为负性液晶。在液晶显示器的结构中,液晶是一层不导电的介质层,夹在像素电极和公共电极之间,则液晶电容相对于一个平行板电容器,其基本表达式为

式中, ε 0 是真空介电常数(8.85418×10 -12 F/m); ε r 是相对介电常数; A 是平行板电容的面积; d 是介质层的厚度。如图3.23所示,当液晶分子水平排列时,其电容值为

图3.23 液晶电容的介电常数
当液晶分子垂直排列时,其电容值为

式中, ε // 和 ε ⊥ 分别是液晶分子长轴和短轴的介电常数。液晶分子的其他排列状态,介电常数介于水平的介电常数和垂直的介电常数之间,即介电常数与液晶分子的旋转角度有关,表示为 ε ( θ )。通过液晶分子在电场中的电偶极和电化率的计算,得到TN型液晶分子的中间排列状态的等效介电常数与液晶分子旋转角度之间的关系曲线,如图3.24所示。TN型液晶盒的相对透过率和液晶电容与施加电压的关系曲线,即 T-V 曲线和 C-V 曲线如图3.25所示。
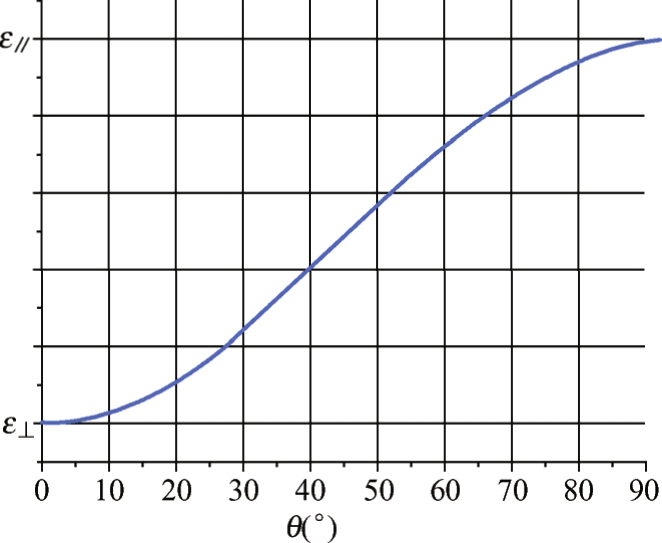
图3.24 TN型液晶分子的等效介电常数与液晶分子旋转

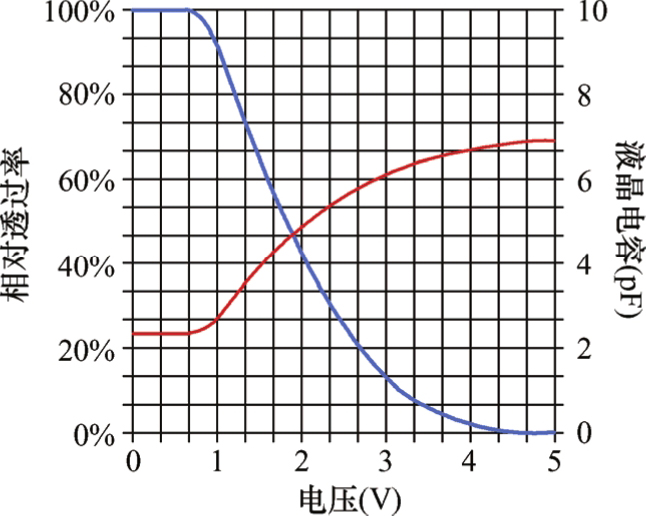
图3.25 TN型液晶盒的相对透过率和液晶电容与施加电

2.液晶动态电容效应
本节前面介绍,液晶电容随着驱动电压的改变或液晶分子的位置关系的改变而改变。在实际的液晶显示器件的驱动过程中,扫描信号电压开启一行的时间约为14.8μs(FHD分辨率,60Hz规格)。由于液晶分子本身存在的黏性和弹性,在这么短的时间内,液晶分子的位置关系基本保持不变,即虽然改变了液晶电容的电压,但是液晶电容还没有改变。期望给液晶分子施加的电压从 0V变更为5V,使液晶的透过率从100%下降到0%,如图3.26所示。刚开始给液晶电容充电的时候,液晶电容上的电压为 0V,此时液晶水平排列,液晶电容值最小(介电常数 ε ⊥ 最小,假设 C LC =2pF);当液晶上的电压为5V时,此时液晶垂直排列,液晶电容值最大(假设介电常数 ε // =3 ε ⊥ ),为6pF。这只是液晶电容的最终数值。因为液晶的响应时间是十毫秒量级,即在行开启的十几微秒内,液晶分子基本保持不动。则在第一次行开启期间,液晶分子上的电压由0V提升到5V,此时液晶电容不变(但是电容上电压必须是连续的),电容上的电荷量为
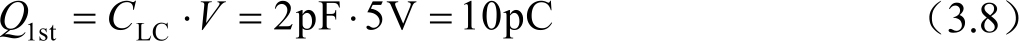
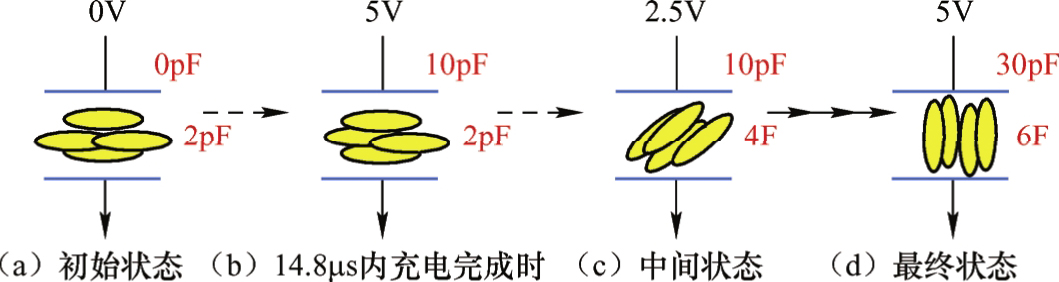
图3.26 液晶动态电容效应示意图
行开启结束后,液晶电容上的电荷处于保持状态,液晶分子在该电压下逐渐进行旋转,液晶电容也开始发生改变。由于液晶电容上的电荷守恒,在1帧的保持时间内(16.7ms),电容提升到4pF,电压则下降为2.5V。因为施加的电压目标值是5V,实现透过率为0%,而经历1帧的时间后,最终的电压为2.5V,透过率还远远没达到0%。第2帧行扫描开启后,此时输入的电压为-5V(极性反转驱动),此时液晶电容上的电荷量为
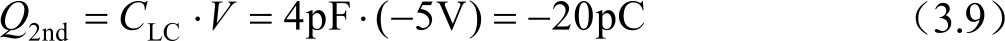
液晶电容再次进入电荷守恒状态。在一帧的时间内,液晶电容由4pF提升到5pF,电压则提升为-4V。再经过第三次充电,液晶电容将由5pF向最终的6pF趋近,电压也由绝对值4V向最终的绝对值电压5V趋近。
从图3.25所示的液晶电容充电和透过率变化的关系中可以看出,让液晶分子的透过率状态完全发生改变,至少需要3帧以上的时间,即相当于液晶显示器的响应时间大大降低了。为了解决这个问题,提高液晶的响应速度,在每一行的数据信号电压局部做了调整。如果是朝着高电压的方向充电,则局部电压调整为比目标电压高些,这种驱动被称为过驱技术(Over-driving);如果是朝着低电压的方向充电,则局部电压调整为比目标电压低些,这种驱动被称为下拉驱动技术(Under-shoot)。过驱技术与下拉驱动技术的主要区别是过驱技术是主动施加更高的电压驱动液晶,而下拉驱动技术仅仅是尽量降低驱动电压,依靠液晶的弹性恢复到原状态。此外,为了降低液晶电容的动态效应的不良影响,每个像素中设计了存储电容,其存储的电量大大减轻了由于液晶电容的变化而引起的电压(即像素电压,与灰阶有关)下降。
3.像素存储电容结构
存储电容是像素电极与一个电位参考电极之间相交叠形成的。根据电位参考电极不同,存储电容有两种结构形式。一种是用公共电极作为电位参考电极,被称为C ST -on-COM,如图3.27(a)所示;另外一种是以该像素上一行的栅扫描线为电位参考电极,被称为C ST -on-Gate,如图3.27(b)所示。它们之间的主要区别在于储存电容的公共电极是利用相邻行扫描线还是一条独立的公共电极走线(Common,简称COM)来完成的,等效电路图如图3.28所示。COM电极电压维持在8V左右(TV面板驱动),而栅扫描线(Gate)在完成行扫描驱动后,电压保持在-8V左右(TFT I off 最低点的电压)。
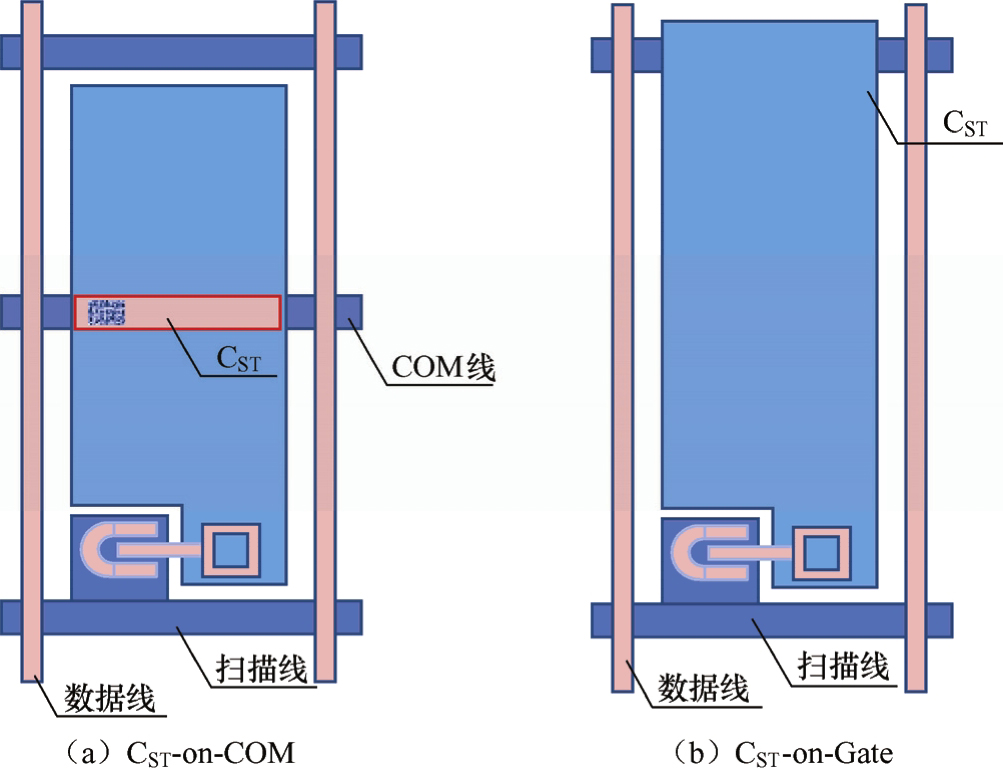
图3.27 像素储存电容的两种结构
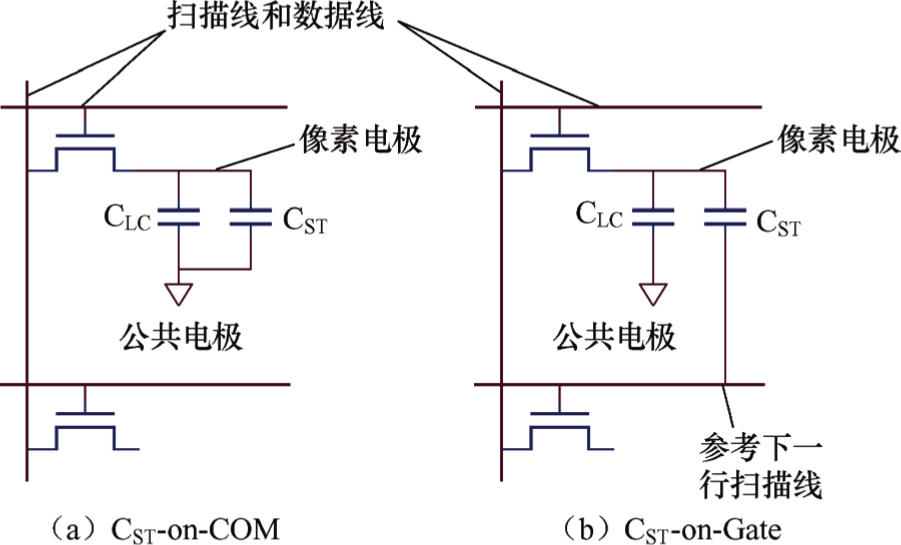
图3.28 像素储存电容的两种结构的等效电路
C ST -on-Gate结构,不需要像C ST -on-COM一样需要额外增加一条电极走线,所以相比较它的开口率(Aperture Ratio)会大些。在像素设计中,开口率的大小是影响面板设计的重要因素。因此,面板的设计大多数会考虑C ST -on-Gate的结构。但是由于电容耦合效应的存在,像素上信号电极电压会受存储电容耦合影响,受到Gate线扫描信号电压变化而发生变化,即影响了像素电压。不过由于Gate线扫描信号电压开启的时间很短,比如,以1920×1080分辨率、60Hz屏幕刷新率的面板来计算,一条Gate线的开启时间约为14.8μs,而1帧画面的时间是16.7ms,因此相比影响有限,即随着该行开启时间的结束,像素电极电压会很快恢复到原电压。
像素存储电容的大小,与介质层厚度和介电常数、交叠面积相关。C ST -on-COM结构如图3.27(a)所示,COM线是金属,它的宽度影响着像素的开口率。为了获得足够大的电容,又不严重影响到像素的开口率,因此,通常在用第一层金属(Metal1,即Gate金属)形成的COM线上也覆盖一层第二层金属(Metal2,即源漏金属),然后开个过孔,这样像素电极ITO就能与Metal2相连接,减少了像素存储电容的介质层厚度,在相同交叠面积下提高了存储电容的数值。与C ST -on-COM结构相比,C ST -on-Gate的电容结构不需要占用像素透光的区域,因此对提高开口率有利。
4.像素等价电路结构及各电容计算
不管哪种像素结构,其基本组成包括导电层薄膜和功能层薄膜。导电层薄膜是指依次扫描每行的扫描金属线、输入数据信号的数据金属线和驱动液晶旋转的像素电极(金属或 ITO 薄膜)。功能层薄膜是指在导电电极之间的绝缘介质层薄膜(SiN x 或 SiO x )、位于金属与半导体薄膜之间起到欧姆接触作用的欧姆接触层薄膜(n + a-Si:H)和半导体层薄膜(a-Si:H或以IGZO为代表的氧化物半导体层薄膜)。在一个像素中,电容可以分为交叠电容和非交叠电容。顾名思义,交叠电容是指组成电容的两个导电电极是互相交叠的,这类电容有Metal1与Metal2之间的各个交叠电容、存储电容和液晶电容,以及公共电极位于彩膜基板时金属电极线与该公共电极间构成的交叠电容。非交叠电容主要是金属线与像素电极之间的电容。当一个电容存在,又不是我们设计上需要的,被称为寄生电容,如两层金属之间的交叠电容。非交叠电容的计算,需要用专门软件才能计算出来。图3.29是C ST -on-COM像素结构(不含源漏金属与COM线交叠)的等价电路结构示意图,这里以此电路图说明各主要电容的计算方法。
参考式(3.5)给出的平行板电容公式,计算各个电容。
(1)存储电容C ST
电容面积 A =像素电极ITO与COM线的交叠面积
介质层厚度 d =像素电极ITO与COM线间的介质层(g-SiN x +PVX)
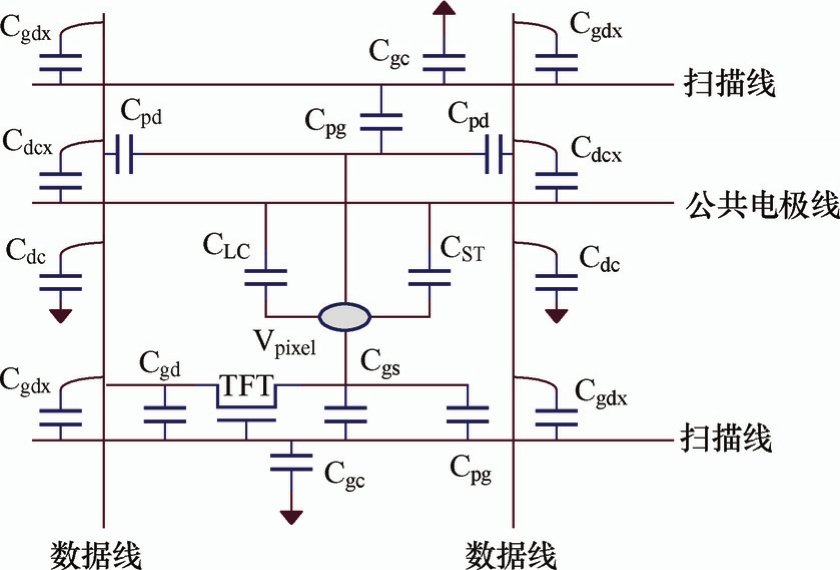
图3.29 C ST -on-COM像素结构的等价电路结构示意图
(2)液晶电容C LC
电容面积 A =像素电极ITO的面积(忽略局部开口区域)
介质层厚度 d =液晶盒厚厚度
由本节前面的介绍可知,液晶电容是个变量。
Metal1与Metal2的交叠电容的计算稍微有差异。如图3.30所示,图中粉色区域是指做源漏金属电极(S/D电极)的Metal2采用了HTM Mask工艺,因此在金属下面有Active层(a-Si:H和n + a-Si:H),而且Active层边缘还往外凸出一定宽度,这个宽度被称为Active Tail(一般在1μm左右)。因为Active Tail是半导体材料,在外电场下具有较强的导电性,所以,Metal1和Metal2间的交叠电容,要针对扫描线负载和数据线计算分别计算。
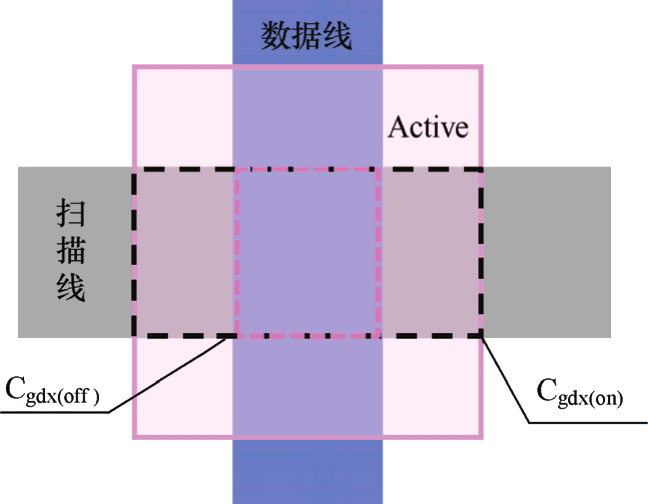
图3.30 HTM工艺的扫描线(Metal1)和数据线

针对扫描线负载计算,即此时该行扫描线开启,Metal1上为高电压(约30V),Active层当作导体;当该行扫描线关闭时,Metal1上为低电压(约-8V),Active层当作绝缘体。
(3)扫描线负载的交叠电容(C gdx(on) )
电容面积 A =Metal1上Active层的交叠面积
介质层厚度 d =Metal1与Active间的介质层厚度(g-SiN x )
(4)数据线负载的交叠电容(C gdx(off) )
电容面积 A =Metal2与Metal1的交叠面积
介质层厚度 d =Metal1 与 Metal2 之间的介质层厚度(g-SiN x 、a-Si:H 和n + a-SiN x )
同样的方法,对于采用HTM工艺TFT上的C gs 和C gd 也分为两种情况,如图3.31所示。
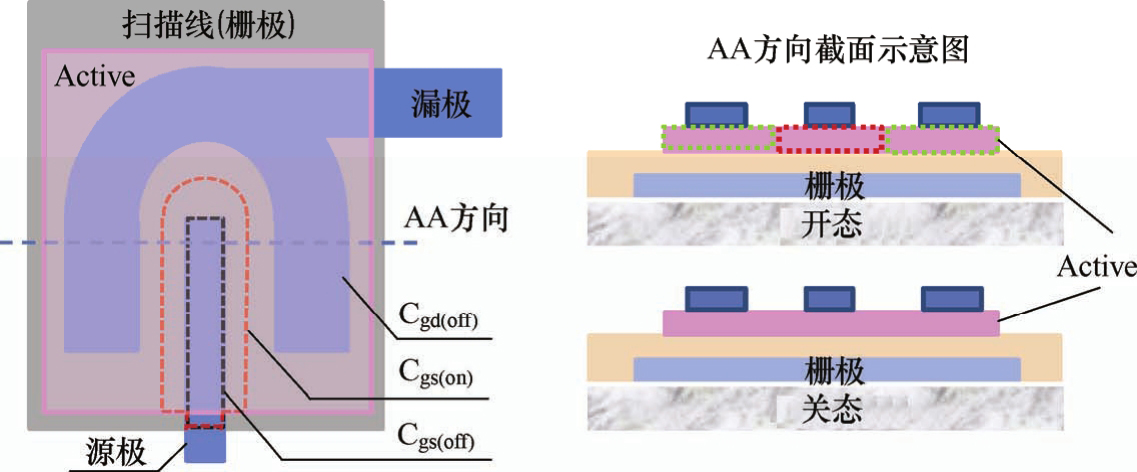
图3.31 HTM工艺的扫描线与TFT的源极和漏极的交

(5)C gs(on)
电容面积 A =Metal1与源极(Source极,S极)的交叠区面积+沟道内Active面积的一半
介质层厚度 d =Metal1与Active间的介质层厚度(g-SiN x )
(6)C gs(off)
电容面积 A =Metal1与源极的交叠区面积
介质层厚度 d =Metal1与Metal2间的介质层厚度(g-SiN x 、a-Si:H和n + a-SiN x )
(7)C gd(on)
电容面积 A =Metal1与漏极(Drain极,D极)交叠区面积+沟道内Active面积的一半
介质层厚度 d =Metal1与Active间的介质层厚度(g-SiN x )
(8)C gd(off)
电容面积 A =Metal1与漏极的交叠区面积
介质层厚度 d =Metal1与Metal2间的介质层厚度(g-SiN x 、a-Si:H和n + a-SiN x )
需要注意的是,上面的计算中,对于开态,除了沟道内的Active面积划分,源极和漏极外边缘的Active Tail也要计算在内。
SiN x 介质层的相对介电常数 ε =6.5,Active层相对介电常数是12。液晶的相对介电常数垂直方向是3左右,平行方向是7左右。
5.电容耦合效应
在一个像素中,不同的导电电极之间,均存在一个电容。这些电容,有的是必要的,如存储电容;有的是不必要但是结构上又无法避免的,如数据信号线与像素电极之间的寄生电容。电容的耦合效应是基于电荷守恒的情况下,不同电极之间通过电容联系在一起,个别电极的电位变化,引起另外一端电位变化的现象。
四个电极通过四个电容连接在一起,如图3.32所示。假设 V A 电压突然变化了Δ V ,则根据电容两端电压不能突变的原理,在电容C 1 上该时刻电位也为Δ V 。由于C 1 与其他三个电容连接在一起,电位最终是一致的,即互相间会有电荷流动最终达到平衡。因此达到平衡后的电位值为
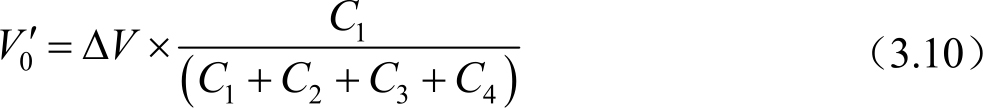
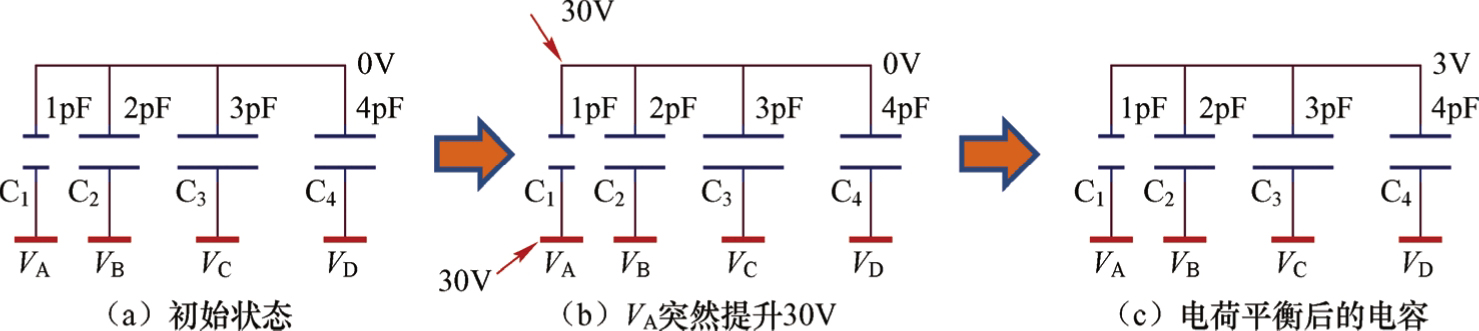
图3.32 电容耦合效应示意图
假设 C 1 =1pF, C 2 =2pF, C 3 =3pF, C 4 =4pF, V A 的电位突然变化了30V,则瞬间 C 1 上的电位也为30V。因为四个电容没有其他电荷泄漏路径,所以电荷是守恒的。因此,最终达到电位平衡,平衡后的电位为
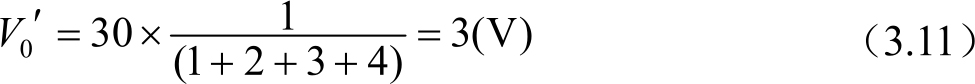
在像素中,对显示影响大的寄生电容是C gs 、C dp 。C gs 引起像素的馈入电压效应。C dp 是引起串扰(Crosstalk)的重要因数之一。对于拼接曝光的阵列图形中,同一层的不同曝光区间,C dp 存在一定的偏差,则像素电极受到的耦合影响也不一样,引起拼接姆拉(Mura),即不同曝光区间亮度不均。理想情况下是恒定电压的公共电极电压 V COM ,实际上其电压在耦合电容的作用下也是波动性的。 V COM 电压的波动性,对串扰和残像都有着重要的影响。为了降低 V COM 电压的波动性,在面板设计上需要采取一些措施。
6.像素馈入电压
在一个像素中,除了主要的存储电容和液晶电容外,还有一些寄生电容存在(见像素等效电路示意图)。像素馈入电压(Feedthrough Voltage)是基于电容耦合效应的原理,在扫描信号电压由开启TFT的高电位下降到关闭TFT的低电位时由于寄生电容耦合引起像素电位的突变电压。这些寄生电容中,栅电极与联通像素电极的TFT源极之间的寄生电容C gs 对像素电压的影响比较大。因为在一行开启时,栅极电压由一个较低的电位(通常是-8V)在瞬间上升到一个高电位(通常是30V),在一行充电时间完成后,这个高电位又瞬间下降到低电位,此时,由于电容耦合效应,刚充电到数据信号电位的像素电极上的电位会被拉下来。即相对C gs 形成了一个转移比:

因此馈入电压可以表示为
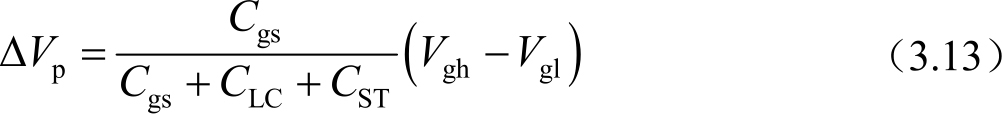
式中, C LC 是个变量,与数据信号电压相关,有最大和最小值,以电学各向异性是正性的液晶来计算,则

式中, A 是像素中液晶电容的面积; d 是液晶盒厚。在常白模式中,当TN型液晶材料的介电常数最低时( ε r = ε ⊥ ),液晶电容最小,显示亮态(此时液晶上的电压最低);随着施加在液晶上的电压增加,介电常数也达到了最大( ε r = ε // ),液晶电容最大,显示暗态。液晶的最大介电常数一般是7~8,而且是最小的两倍以上。馈入电压差值为
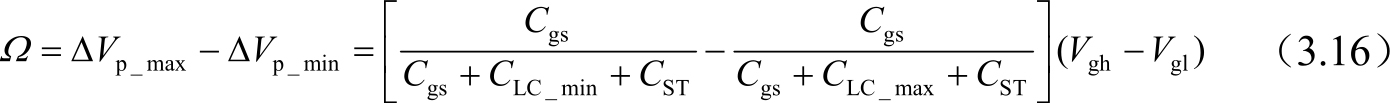
在像素充电的示意图中,如果没有馈入电压的影响,则为了实现液晶的等电压交流驱动,公共电极电压应该为

存在馈入电压,则公共电极电压就需要适当下调,起到液晶上正负电压平衡的作用,即
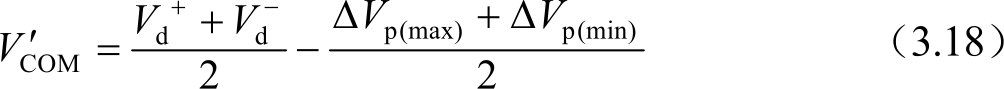
在面板的输入端, V COM 一般是一个稳压输入源。由于Δ V p 不是固定值,说明公共电极电压的调整,只能选取一个最佳值。即如果馈入电压差值 Ω 较大,则液晶上会出现交流电压成分,容易引起画面闪烁(Flicker)和残像(Image Sticking)。对于C ST -on-Gate的存储电容结构,可以从上一行扫描线引入一个补偿脉冲,能补偿上式的馈入电压偏差,或者对公共电极电压进行适当偏移。
3.5.2 像素中电阻计算
一块液晶显示器中,像素区占据了绝大部分区域,因此扫描线和数据信号线的电阻和电容负载,主要也是在像素区。计算出单个像素的电阻和电容,就很容易得到像素区的总电阻和电容。
像素中的扫描线或数据线,形状可能是规则的,也可能不是规则的。图3.33所示为一个像素内的规则图形和非规则图形的薄膜线电阻计算方法。表征薄膜的电阻用方块电阻,即 R s ,其单位是Ω/□。薄膜的方块电阻 R s 与其电阻率 ρ 和薄膜厚度之间的关系:

式中, t 是薄膜的厚度。定义导电薄膜沿着电流的方向长度为 W ,电流的导电截面宽度为 L ,则规则的导电电极线的线电阻为

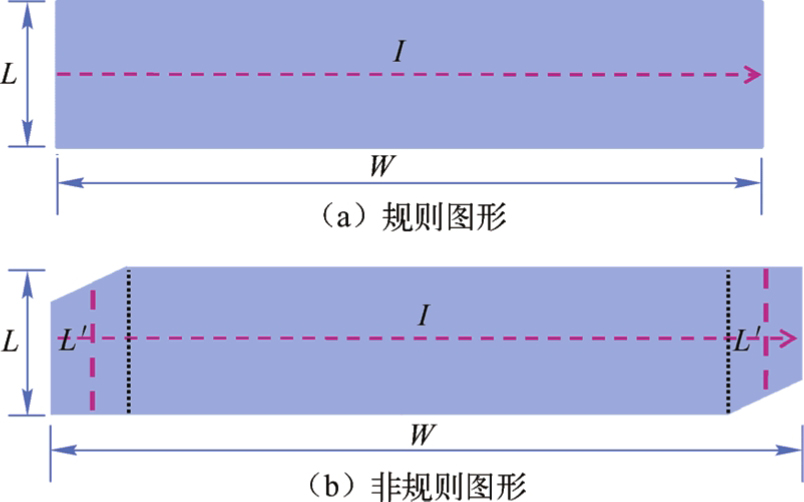
图3.33 规则图形和非规则图形的电阻计算
对于不规则的线电阻计算方法,可以把不规格部分分割出来。不规则区是个梯形,则用梯形的中位线宽度设定为 L ′即可。各段线电阻之和即为该非规则图形的线电阻。像素内的线电阻计算出来后,根据显示器分辨率即可得到像素区的总电阻了。ITO的 R s 一般为65Ω/□,金属薄膜的 R s 一般为0.1Ω/□。
3.5.3 TFT性能要求
1.TFT开关比的要求
TFT开关比是指开态电流和关态电流的比值。这个比值对像素电压保持率非常重要。因为在一帧画面更新中,一行的开启时间很短(如14.8μs),所以需要大的开态电流;开启后该像素需要保持1帧的时间(如16.7ms),所以要确保关态电流很小。开态电流随着 TFT 的源漏两端电压的变化而变化,关态电流也是与TFT的源漏两端电压相关。这里以一个相对稳定的数值来说明TFT的开关比的要求。其中 I charge 指TFT的开态电流, I leakage 指TFT的关态电流。给一行的像素充电,可以描述为
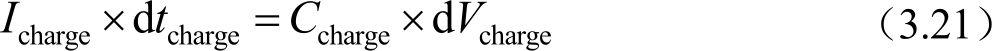
以8bit数据FHD分辨率60Hz驱动的液晶屏来说明,则一行的充电时间约为14.8μs;像素充电的电位相比 V COM 电位,与上一帧是相反的,其最大跨幅就是数据信号电压的最大与最小之间的幅值,这里假设为10V。
一行的像素充电完毕,其保持特性可以描述为
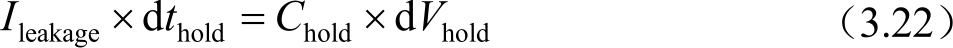
式中,d t hold 和d V hold 分别是1帧的时间和1帧时间内电压的变化量。8bit的最小灰阶电压为8mV,即要确保像素的灰阶不变化,则d V hold =8mV。 C charge 与 C hold 都是液晶电容和存储电容之和,液晶电容存在最大值和最小值,两者相比差异达到3.5倍左右(液晶长轴和短轴的介电常数不一样造成的)。
由上面两个式子可以得到
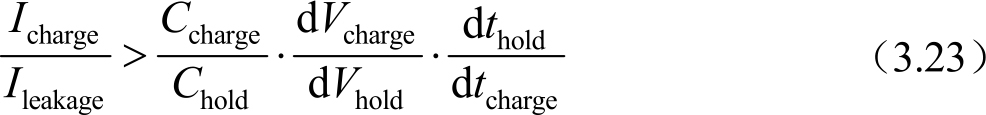
即

上面的计算都是在最苛刻的情况下进行的。如果开态电流和关态电流比值不充分,则像素充电不充分(液晶光效没有达到最大)或即使充电充分,但是不能保持灰阶所要求的最低电位。在液晶显示中,TFT的开态电流和关态电流在是否有光照射的情况下差异也比较大。因此设计中,需要参考暗态的TFT开关比,更需要考查亮态的TFT开关比。
2.TFT开态电阻和关态电阻
像素的充电,与像素中的液晶电容和存储电容息息相关。为了确保像素充电率或充电后的保持率,需要确保像素的目标电压变化量小于最低有效位(Least Significant Bit,LSB)电压的一半,即0.5LSB。从VT曲线和Gamma曲线可以看出,在透过率相对高或相对低时,不同灰阶间的亮度变化不明显,即对应不同灰阶的数据信号电压变化了,但是亮度变化不明显;而在中间灰阶区域,不同灰阶间的亮度变化非常明显。为了让人眼感觉到亮度与灰阶间是按照等级来变化的,即一个灰阶对应一个亮度等级,则在透过率相对高或相对低时灰阶间的电压间隔大,而中间透过率区间灰阶间的电压间隔小。对于一个8bit数据信号驱动的常白显示模式液晶显示器,液晶的阈值电压是1.2V以及液晶完全开启的电压是4.06V。则由VT曲线得到,在电压1.2V、2.15V和4.06V时分别对应“全亮”、“中间灰度”和“全黑”。从“全亮”到“全黑”之间共有256个灰度等级(灰阶)。如果是线性的8bit信号驱动,则灰阶的LSB为
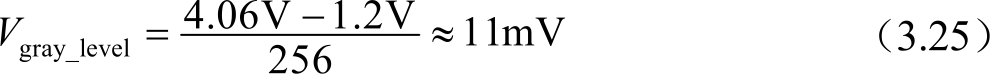
在像素充电过程中,像素的目标电压误差要小于0.5LSB,即小于5.5mV。因此,相对上述三个电压值,该电压差值的充电电压误差率(Charging Voltage Error, Δ )分别为0.46%、0.256%和0.135%。在像素充电过程中,TFT的沟道电阻 R on 与像素电容(主要是 C LC 和 C ST )的时间常数为

则充电电压误差率为

式中, t 是行开启时间。 t =6 τ 时, Δ =0.25%; t =7 τ 时, Δ =0.09%。要实现上述的电压误差率,行开启时间需要6倍多的时间常数,这对于高分辨率的显示器来说是非常难实现的。上述说的是等灰阶线性8bit的数据信号驱动,对应的亮度不是线性的。一般显示器中,我们期望得到亮度的变化是线性的,即灰阶变化与亮度变化是线性的,需要等亮度非线性8bit的数据信号驱动,此时对应的“中间灰度”的LSB=6.6mV。即相比等灰阶线性8bit驱动,等亮度非线性8bit的驱动实现像素电压误差率小于0.5LSB(3.3mV),行开启时间需要7 倍的时间常数。因为是等亮度非线性8bit驱动,因此对应的亮度偏差为[1/(256×2)]=0.2%。
像素充电的动态响应如图3.34所示。在像素充电期间,TFT上的栅极电压逐渐升高,TFT的工作状态由关态,经过亚阈值区,再到饱和区( V ds > V gs -V th ),然后进入线性区( V ds < V gs -V th )。接着,当栅极电压下降时,TFT的工作状态是由线性区到饱和区,然后是亚阈值区,最后到关态。从图3.34中可以看出,像素充电期间的大部分时间里TFT是工作于线性区,TFT的沟道电流遵循逐次沟道近似原理,即线性区TFT沟道电流为
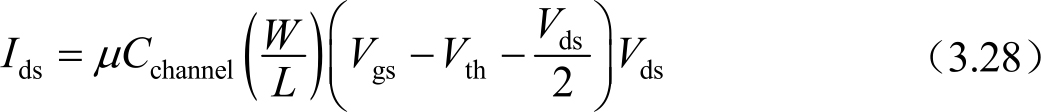
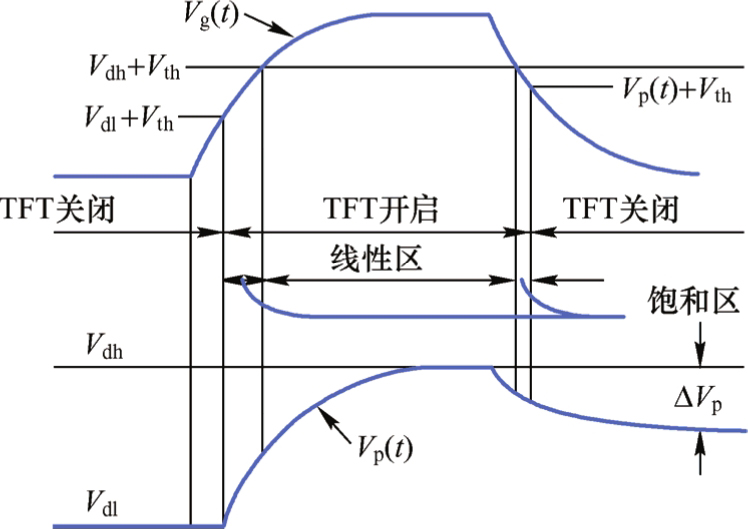
图3.34 像素充电的动态响应示意图
式中, C channel 是沟道电容; W 和 L 分别是TFT沟道宽度和长度; μ 是沟道有效载流子迁移率; V th 是阈值电压。在线性区,TFT的开态电阻 R on 可以表达为
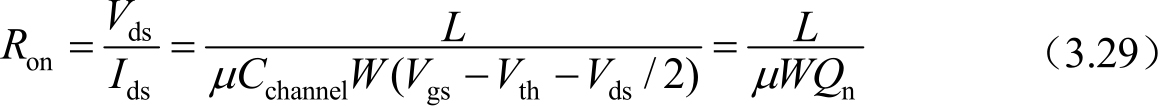
式中, Q n 表示沟道中载流子的电荷密度(C/cm 2 )。如前所述,像素充电到像素的目标电压要小于 0.5LSB,即像素充电的电压误差率要介于 0.09%~0.25%需要 6倍以上的时间常数。以6倍时间常数计算,时间常数可以表达为
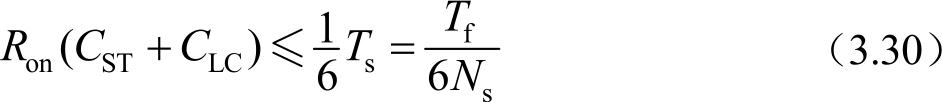
或表示为

式中, T s 是指行扫描时间; T f 是一帧画面的扫描时间; N s 是指显示器的行扫描线数。在实际的像素充电中,考虑到扫描信号的延迟,一行的扫描时间需要满足
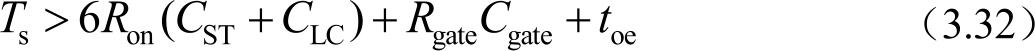
式中, R gate C gate 是行扫描信号的时间常数; t oe 是扫描信号和数据信号位移时间。 R gate C gate 在数值上是指栅电压上升到目标电压的 63%所需要的时间,经过这段时间后,可以认为 TFT 沟道具有足够的电流导通能力。 t oe 时间设定的目的是避免栅扫描信号下降的延迟期间(TFT 没有完全关闭),数据信号极性的转变而引起像素充电串扰,数值上包括行扫描信号下降延迟时间和数据信号极性转变的延迟时间。如果采用预充电,则目标充电行提前一行开启,而且目标像素电位提前进行预充电,则可以不考虑行扫描上升期间信号延迟的影响,即式(3.32)中的 R gate C gate 可以忽略。
通过上面式子,也可以得到沟道迁移率的要求:
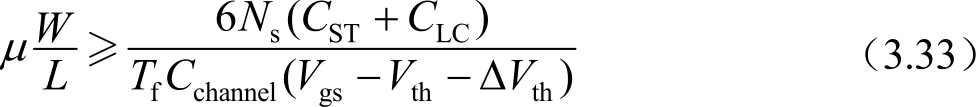
式中,Δ V th 是阈值电压的漂移值。在薄膜晶体管中,多种因素会导致阈值电压逐渐漂移,比如:(1)栅绝缘层存在大量的缺陷态,外电荷注入引起的阈值电压漂移;(2)半导体层在电应力作用下(Si—H) x 基团弱键断裂形成缺陷引起的阈值电压漂移等等。阈值电压的漂移是影响液晶显示器寿命的关键因数。随着阈值电压漂移的增加,显示品质逐渐下降。通常在显示器寿命期,Δ V th 变化量不超过5V。
两个因数会引起闪烁,即像素的正极性和负极性周期的净亮度变化和TFT关态期间的漏电流引起的亮度变化。因此,要求TFT的关态漏电流必须满足:
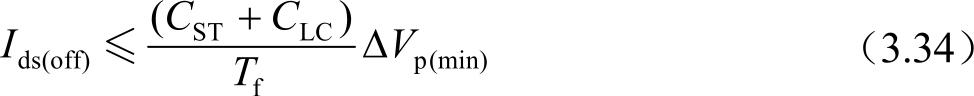
式中,Δ V p(min) 是像素电压的最小变化量,超过此变化量,则人眼或测试仪器能探测到。像素关态的时间常数可以表达为
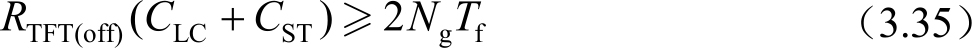
式中, N g 是灰阶数。对于一个电压误差率为0.5LSB的8bit线性驱动器,由上面两个式子合并可以得到

上式说明TFT的开态电阻与其关态电阻呈正比关系,而且分辨率越高或灰阶级数越高的显示器,对TFT的开关电阻比值提出了更高的要求。对于一个8bit 256灰阶的FHD( N s =1080)分辨率的像素量的显示器,由式(3.36)可以得到

在理想情况下,TFT的关态漏电流主要由半导体材料的a-Si:H薄膜引起。因此,关态漏电流可以表达为

式中, σ D 是a-Si:H薄膜的暗电导率; d 是其薄膜的厚度; V ds 是TFT沟道间的电压。由于 σ D 随着a-Si:H薄膜的厚度 d 下降而下降,因此为了获得更低的关态电流,通常会选择比较薄的a-Si:H薄膜做沟道层。在BCE(Back Channel Etching)结构中,a-Si:H薄膜厚度一般在100nm以上,而在ESL(Etching Stopper Layer)结构中,a-Si:H薄膜厚度一般在50nm左右。在BCE结构中,a-Si:H薄膜更厚些,主要是因刻蚀 n + a-Si:H 时应确保有足够的刻蚀余量。上面两个方程式所要求的TFT关态电流是从不同角度进行分析的。在背光源的照射下,作为半导体的a-Si:H具有光电导,因此也会引起光生电流,即引起TFT的关态电流增加。一般来说,在一个像素中,关态漏电流的泄漏路径主要有以下几种。
(1) TFT的源极与漏极之间( I ds );
(2) TFT沟道的光生漏电流( I photo );
(3)绝缘层的缺陷态引起的漏电流( I SiN x );
(4)液晶材料杂质引起的漏电流( I LC )。
研究表明,TFT的开态电阻和关态电阻的比值是环境温度的函数。温度每增加20℃,TFT的关态电流约增加一个数量级,而开态电流约增加2μA,即开关比随着温度升高而下降。
3.5.4 像素充电率模拟
1.输入信号延迟
在显示面板的像素阵列中,以满足每个像素的充电为单元,则其输入信号总线电阻和总线电容的效应可以简化为一级电阻和电容RC的低通滤波器电路。由以上计算得到的一条信号线上单个像素相关的电阻和电容分别为 R 和 C ,如果整条信号线有 N 个像素,则该条信号线可以看作一维分散型RC串联电路,如图3.35所示。其中A点是Gate信号的输入端,B点是Gate输入信号的末端,也就是充电像素的Gate信号。在直流驱动下,电容不导通,则A点和B点等电位。如果A点的电位稳定地向另外一个数值变动( V 1 变动到 V 2 ),则变化期间,B点电位也会由 V 1 变化到 V 2 。但是在这个一连串的低通滤波器中,高频信号成分会被分压而递减,导致通往B点的各节点电压与输入端信号电压波形不一样,出现延迟的情况,这就是设计中提到的信号延迟。对B点电位的变化,可以近似为指数形式由 V 1 向 V 2 改变:
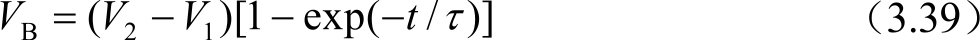
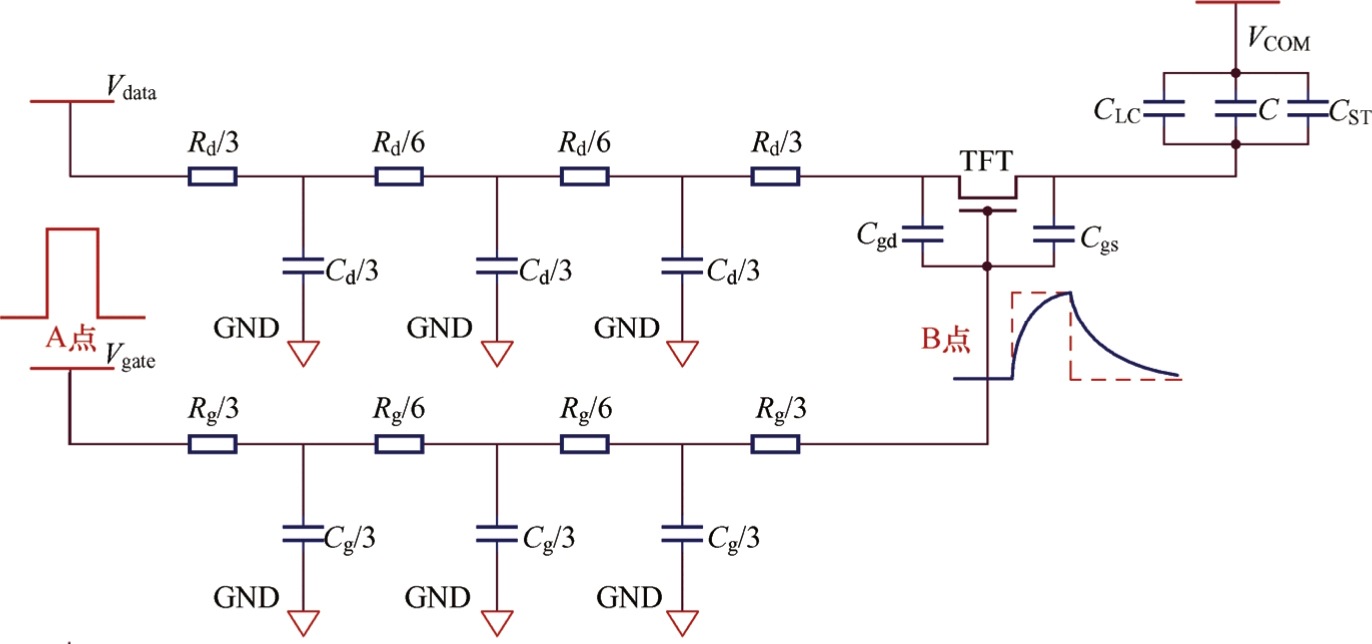
图3.35 单个像素充电的一维分散型RC串联电路网络示意图
式中,时间常数 τ 近似为
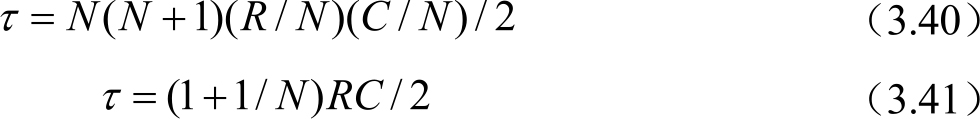
即只要计算出该信号线总的等效电阻和电容,就可以得到近似的延迟信号的电压波形。
举例子说明。32in的HD分辨率液晶面板,扫描信号线的总电阻为3.5kΩ,总电容为887pF,总像素串联数有4098个。信号输入端电压由0V提升到30V,并在20μs后回落到0V。则由式(3.39)计算得到

实际经验表明,当 N ≥3时,延迟波形与取值 N 时的延迟波形基本一致。而且取值偏小,相当于高估了信号延迟时间,是一种保守的设计评估方法,以确保设计有更大的冗余。
2.充电率模拟
像素充电波形如图3.36所示。假设行扫描信号高电平为 V gh ,低电平为 V gl ,数据信号低电平为 V dl ,高电平为 V dh ,则行开启期间,像素电压波形为
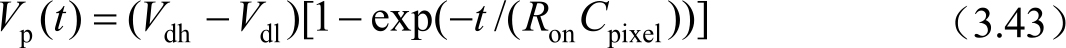
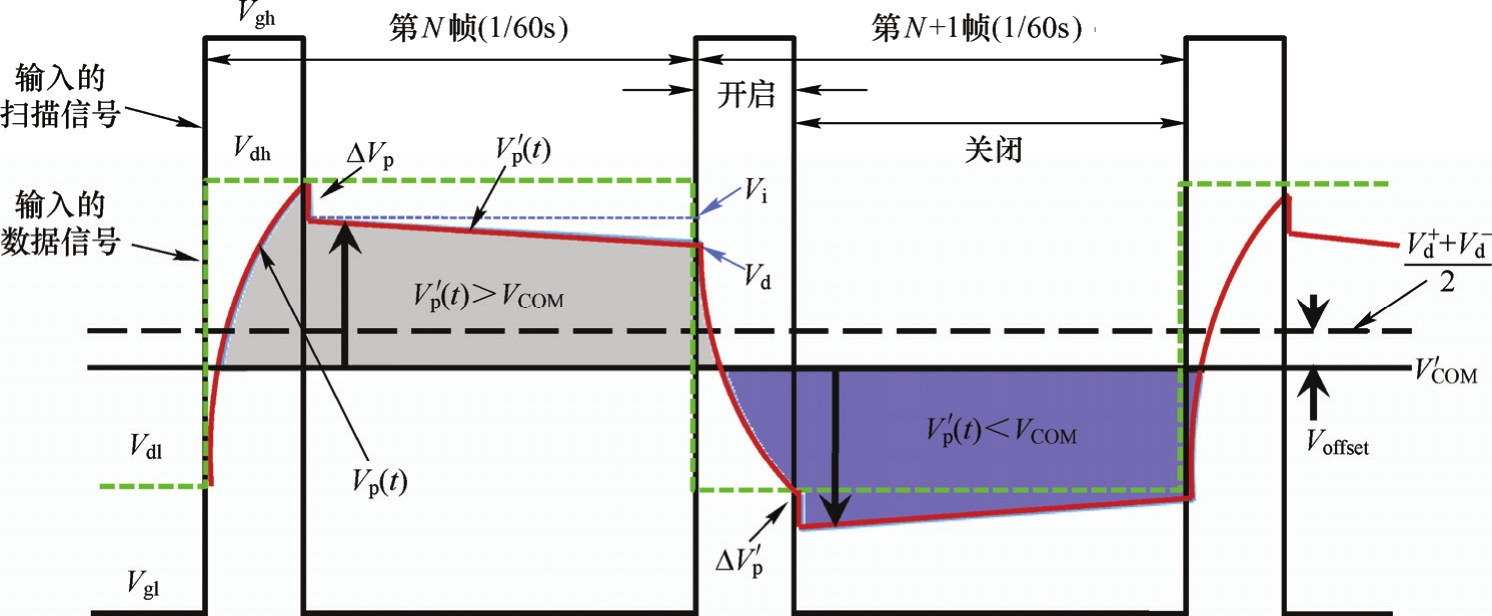
图3.36 像素充电示意图
当 t =6 · R on C pixel 时, V p ( t )=0.9975( V dh − V dl ),即像素充电率:
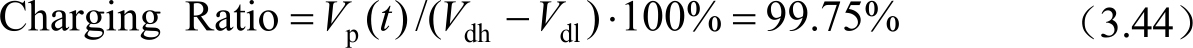
在行扫描结束后,由于馈入电压的影响,像素电压下降为 V i ;在1帧时间内,由于像素漏电的影响,像素保持电压 V p ′( t )会发生变化,在1帧即将结束时为 V d 。在1帧时间内,像素起始端电压 V i 和结束端端电压 V d 的变化差是引起画面闪烁的原因之一,而且闪烁频率与帧速一致,属于60Hz的闪烁成分。由于馈入电压Δ V p 不是固定值,则两帧之间的 V i 电压可能不一样(当 V COM 电压没有很好补偿),这是引起画面闪烁的另外一个原因,属于 30Hz 的闪烁成分。为了降低闪烁,可以采取的措施有增加存储电容、降低馈入电压(减小 C gs )、降低关态漏电流和采用三阶/四阶扫描线补偿驱动方式。


