第二章
PageRank
——
让谷歌腾飞的技术
《星际迷航》( Star Trek )中的计算机并不特别让人感兴趣。他们向计算机提问题,计算机还要想一会儿才能回答。我觉得我们能做得更好。
——拉里·佩奇
从建筑学的角度来说,车库是简陋的地方。但在硅谷,车库有一种特殊的创业含义:许多伟大的硅谷技术公司在此诞生或至少从车库中“孵化”而来。这一趋势并非从20世纪90年代的互联网泡沫(指1995年至2000年围绕互联网公司形成的投机性投资泡沫)开始。在互联网泡沫出现的50多年前的1939年,当世界经济仍未从大萧条的影响中走出来时,惠普(Hewlett-Packard)就在加利福尼亚州帕罗奥图市(Palo Alto)戴夫·休利特(Dave Hewlett)的车库中逐渐成形了。几十年之后,史蒂夫·乔布斯(Steve Jobs)和史蒂夫·沃兹尼亚克(Steve Wozniak)于1976年在加利福尼亚州洛斯拉图斯市乔布斯的车库中创业,之后创建了今天堪称传奇的苹果计算机公司。(尽管传说苹果公司创建于车库,但乔布斯和沃兹尼亚克一开始其实是从一间卧室开始的。空间很快就不够用了,于是他们转移到了车库。)不过,和惠普与苹果的成功故事相比,一个名为谷歌的搜索引擎的创建过程更令人惊叹。谷歌从加利福尼亚州门洛帕克市的一间车库开始,并于1998年9月注册成立公司。
那时,谷歌事实上已经运营自己的搜索引擎一年多了——最开始是在斯坦福大学的服务器上,谷歌的两位联合创始人都是斯坦福博士生。直到斯坦福大学再也不能承受这一日益受欢迎的服务所需要的带宽,拉里·佩奇和谢尔盖·布林才把公司转移到了如今著名的门洛帕克车库。他们肯定做了一些正确的事,因为在他们正式成立公司3个月后,美国《个人计算机杂志》( PC Magazine )就宣布谷歌是1998年美国排名前一百的网站之一。
这也是我们的故事真正开始的地方:在《个人计算机杂志》当年的评论中,谷歌的精英管理层因为谷歌“以超乎寻常的技巧得出相关度极高的结果”而获奖。你也许还记得上一章提到过,第一个商业搜索引擎于4年前的1994年发布。还在车库里的谷歌怎么能弥补4年的巨大差距,在搜索质量上超越已经很受欢迎的Lycos和AltaVista呢?这一问题的答案可不简单。但重要的因素之一——尤其是在网络搜索早期——就是谷歌用来对其搜索结果进行排名的创新算法:一个被称为PageRank的著名算法。
“PageRank”是个双关词:它既是一种对网页排名的算法,又是其主要发明者拉里·佩奇的排名算法。佩奇和布林在1998年的一篇学术会议论文《解析大规模超文本网络搜索引擎》( The Anatomy of a Large-Scale Hypertextual Web Search Engine )中发表了这一算法。正如论文标题所暗示的那样,这篇论文的内容不只是描述PageRank。事实上,这是对1998年存在的谷歌系统的完整描述。但藏在这一系统技术细节中的,是对也许是21世纪出现的第一个算法瑰宝的描述:PageRank算法。在本章,我们将探索这一算法如何以及为什么能在“草垛中寻针”,并持续为搜索查询提供最相关的结果,也就是排名最靠前的“命中”。
超链接把戏
你很有可能已经知道了超链接是什么:超链接是网页上的一个短语,当你点击它时,你将被带到另一个网页。绝大多数网络浏览器用蓝色底线显示超链接,以便其能被轻易识别。
令人意外的是,超链接也是老想法。1945年——大约是开始研发电子计算机的同一时期——美国工程师范内瓦·布什(Vannevar Bush)发表了一篇极具前瞻性的论文《诚若所思》( As We May Think )。在这篇涉猎广泛的论文中,布什描述了大量可能实现的新技术,包括一台被称作麦麦克斯(memex)的机器。麦麦克斯可以存储文件并自动进行索引,但其功能远不止这些。麦麦克斯允许“关联索引……任何被选中的东西都能立即自动选择另一个东西”,换句话说,那是一种早期的超链接。
超链接自1945年起就已出现。它们是搜索引擎用来进行排名最重要的工具之一,而且是谷歌PageRank技术的基础。接下来,我们将开始以最大的热情探索PageRank技术。
理解PageRank的第一步是一个名为超链接把戏(The Hyperlink Trick)的简单想法。用一个例子就能非常容易地解释这个把戏。假设你对学习如何制作炒蛋感兴趣,并且用网络搜索了这一主题。如今,任何一次真正搜索炒蛋的网络搜索都会出现数百万个“命中”,但为了方便起见,让我们想象只有两个网页出现:其中一个是“欧尼的炒蛋菜谱”,而另一个则是“伯特的炒蛋菜谱”。这两个网页都出现在下图中,与之一道的是拥有这些菜谱超链接的网页。还是为了方便起见,让我们想象这四个包含超链接的网页是整个互联网上仅有的链接到两个菜谱网页之一的网页。图中底部画线的文字就代表超链接,而箭头则表示链接的指向。

图11 超链接把戏的原理。上面显示了6个网页,每个框都代表1个网页。其中2个网页是炒蛋菜谱,其余4个网页都有这些菜谱的超链接。超链接把戏认为伯特的网页比欧尼的网页排名高,因为伯特有3个链入链接(incoming link),而欧尼的只有1个
问题是,这两个“命中”哪个应该有更高的排名,是伯特还是欧尼?人们在阅读链接这两份菜谱的网页并做出评价时不会有太大的问题。看起来这两份菜谱都很合理,但人们对伯特菜谱的反响要更为热烈一些。因此,在没有给出其他信息的情况下,伯特的菜谱比欧尼的菜谱排名更高可能会更合理。
不幸的是,计算机并不擅长理解网页的真实意思,因此搜索引擎检查这四个链接“命中”的网页,并对每份菜谱获推荐的强烈程度进行评估也不太可能。另外,计算机在计算方面非常优秀。一种简单方法就是只计算链接每份菜谱的网页数——在这个例子中,1个网页链接欧尼的菜谱,3个网页链接伯特的菜谱——并根据这些菜谱的链入链接数对菜谱排名。当然,这种方法远不如让人阅读所有页面并手动排名精确,但它无疑是一种有用的方法。如果你没有其他信息,一个网页的链入链接数可能成为该网页“有用性”或“权威性”的指标。在这个例子中,伯特的菜谱得分为3,欧尼的菜谱得分为1,因此在搜索引擎向用户展示的结果中,伯特的网页排名比欧尼的高。
你可能已经发现了一些在排名上使用这种超链接把戏的问题。一个很明显的问题就是,有时候链接被用来显示差网页,而非好网页。比如,假设有个链接欧尼菜谱的网页上写着:“我试了下欧尼的菜谱,很糟糕。”像这样批评而非推荐一个网页的链接,的确会导致超链接把戏将网页的排名拔高。不过,在现实中,超链接更多是用于推荐而非批评。因此,尽管有这个明显的缺陷,超链接把戏仍然很有用。
权重把戏
你可能已经在想,为什么要对网页的所有链入链接一视同仁,来自专家的推荐肯定就要比“菜鸟”的推荐更有价值吗?要细致地理解这一点,我们就要继续研究上面的炒蛋例子,不过研究的是另一组链入链接。下页的图对链入链接进行了重新设置:现在,伯特和欧尼菜谱的链入链接数相等了(只有一个),但欧尼的链入链接来自我的主页,伯特的则来自著名主厨艾利斯·沃特斯(Alice Waters)。
如果没有其他信息,你更喜欢哪份菜谱?很显然,选择由一位著名主厨推荐的菜谱,要比选择由一名计算机科学相关书籍作者推荐的菜谱更好。我们称这一基本原则为“权重把戏”(The Authority Trick):来自高权重网页的链接排名要比来自低权重网页链接的排名高。
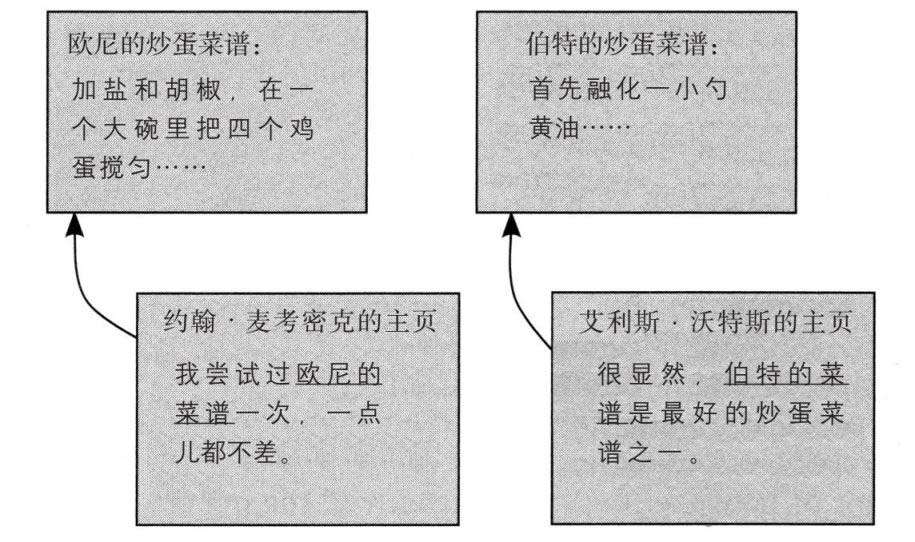
图12 权重把戏的原理。这里显示了四个网页:两个炒蛋菜谱网页和两个链接菜谱的网页。其中一个链接来自本书作者(不是著名主厨),而另一个链接来自著名主厨艾利斯·沃特斯的主页。权重把戏将伯特的网页排在欧尼的菜谱之前,因为伯特的链入链接权重比欧尼的链入链接权重大
这个原则很好,但其目前展示的形式对搜索引擎而言毫无用处。计算机如何才能自动判定艾利斯·沃特斯在炒蛋方面比我更具有权威性呢?有个想法也许会对此有所帮助:让我们把超链接把戏和权重把戏结合起来。所有网页的初始权重值(Authority Score)都是1,但如果一个网页有链入链接,在计算该网页权重时就要加入指向其网页的权重。也就是说,如果X和Y网页链接Z网页,那么Z网页的权重就是X网页和Y网页权重相加的值。
下面的图详细地解释了如何计算这两个炒蛋菜谱网页的权重值。终值显示在圆圈中。图中有两个网页链接我的主页——这些网页本身没有链入链接,因此权重值为1。我的主页的权重值是所有链入链接权重值的总和,相加得2。艾利斯·沃特斯的主页有100个链入链接,每个链入链接的权重值为1,因此它的权重是100。欧尼的菜谱只有一个链入链接,但这个链入链接的权重值是2,因此将其所有链入链接的权重值相加(这个例子中只有一个数可加),能得出欧尼菜谱网页的权重值为2。伯特菜谱网页也只有一个链入链接,但其权重值为100,因此伯特菜谱网页的权重值为100。而因为100大于2,所以伯特的网页排名要比欧尼的高。
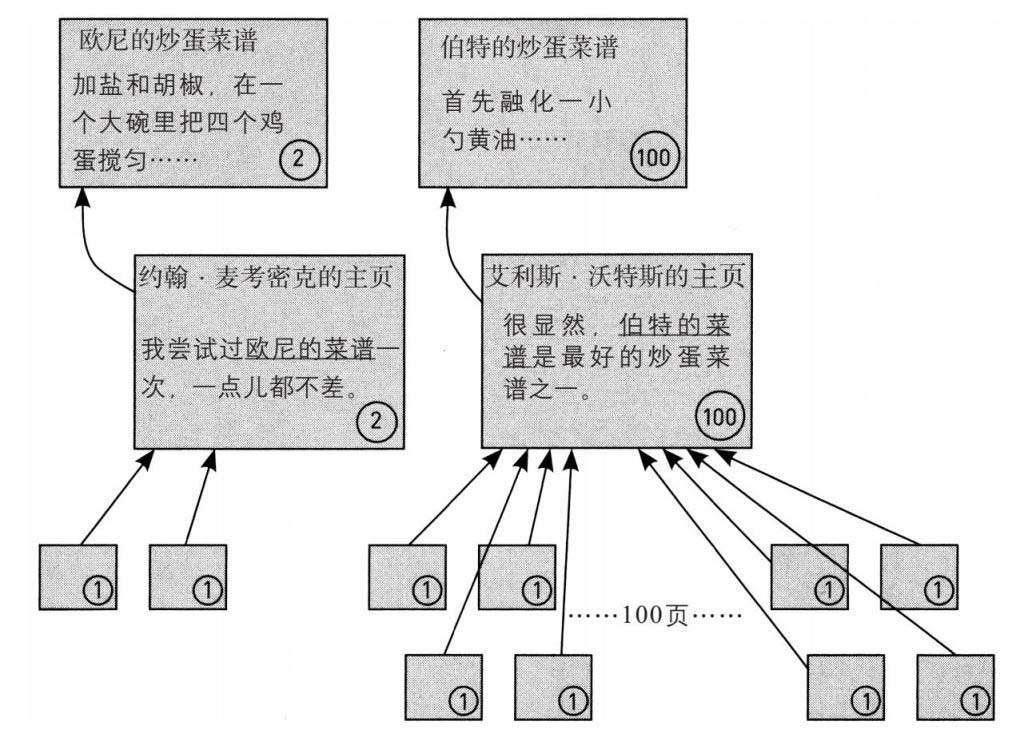
图13 对两个炒蛋菜谱网页权重值的简单计算。权重值显示在圆圈中
随机访问者把戏
就自动计算权重值来说,我们似乎拥有了一个真正奏效的策略,无须计算机真正地理解网页内容。不幸的是,这种方法有个大问题。超链接很有可能形成被计算机科学家称为“循环”(cycle)的东西。循环指访问者可以通过点击超链接返回出发时的网页。
下图就是个例子。图中有A、B、C、D、E五个网页。如果从A开始,我们可以通过A访问B,然后又从B访问E,而我们从E又能点回A,也就是回到了出发点。这也意味着A、B和E三个网页组成了一个循环。
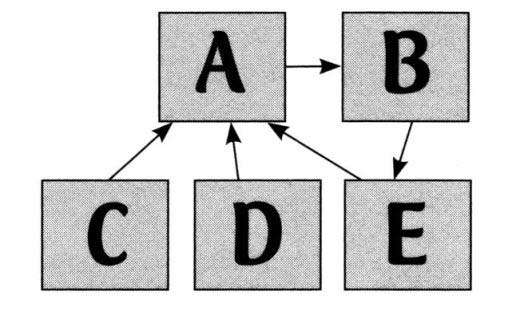
图14 超链接循环的一个例子。网页A、B和E组成了一个循环,你可以从A开始,点击到B,然后到E,再返回出发点A
看来,在遇到循环时,目前权重值的定义(将超链接把戏和权重把戏结合起来)就碰到大麻烦了。看看在这个特例中会发生什么事情。网页C和D没有链入链接,因此其权重值为1。网页C和D都链向网页A,因此A的权重值是网页C和D权重值的和,也就是1+1=2。B网页从A获得的权重值为2,而E又从B获得权重值2。(这里谈到的情况都由下图左侧部分所体现。)但现在A的权重值要更新了:A从C和D各得到权重值1,但A也从E得到权重值2,相加为4。于是B的权重值也需要更新:从A获得权重值4。然后E的权重值也要更新,因为它从B获得了权重值4。(现在谈到的情况都由下图右侧部分所体现。)依此类推:于是A的权重值变为6,B变为6,E变为6,于是A的权重值又变为8……随着循环进行,网页的权重值会一直增加。
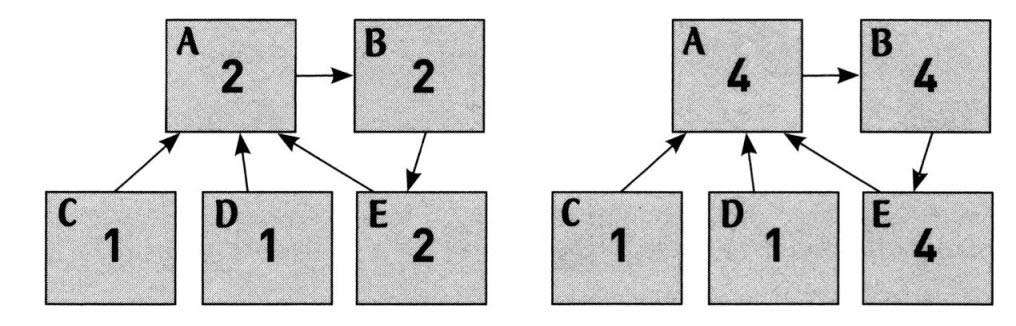
图15 循环造成的问题。网页A、B和E永远需要更新,因此它们的权重值会一直增加下去
这样计算权重值,会产生“鸡生蛋还是蛋生鸡”的问题。如果我们知道A网页真正的权重值,我们就能计算B网页和E网页的权重值。而如果我们知道B网页和E网页真正的权重值,我们就能计算A网页的权重值。但由于这些网页彼此依赖,这样计算似乎根本行不通。
幸运的是,我们可以通过被称为随机访问者把戏(The Random Surfer Trick)的技术解决这个“鸡生蛋还是蛋生鸡”的问题。注意:对随机访问者把戏的初始描述,和到目前为止探讨的超链接及权重把戏没有任何关联。一旦了解了随机访问者把戏的基本原理,我们就会做一些分析,揭示其令人瞩目的品质:随机访问者把戏结合了超链接及权重把戏令人喜爱的属性,但在出现超链接循环时也行得通。
这个把戏从假想一个随机访问互联网的人开始。确切地说,访问者随机从万维网上的一个网页开始访问,然后检查该网页上的所有超链接,之后随机挑选出其中一个超链接进行点击。随后,用户再检查打开的新网页,并随机选择一个超链接打开。这个过程会持续进行,每个网页都是通过随机选择前一个网页上的链接被打开的。图16就是个例子。在这个例子中,我们假设整个万维网只有16个网页。框代表网页,箭头代表网页之间的超链接。我们在其中标记了四个网页以便稍后进行参考。被访问者访问的网页用灰色表示,黑色箭头代表访问者点击的超链接,虚线箭头代表随机重新开始访问,这个在之后会讲到。
整个过程有一个转折点:每次访问一个网页时,都有一个固定的重新访问概率(大概是15%),让访问者不从已有的超链接中挑选一个并点击。相反,访问者会重新开始这一过程,从互联网上随机选择一个网页点击。你也可以认为访问者有15%的概率对任何已有网页厌倦,导致其点击另一组链接,这么想也许会有帮助。要想找些例子,请仔细观察图16。这个特定的访问者从网页A开始,在对网页B厌倦前连续点击了三个随机超链接,并在网页C重新开始。在下次重新开始前,访问者又点击了两个随机超链接。(顺便说一句,本章中所有随机访问者例子中的重新开始概率都为15%,这也是谷歌联合创始人拉里·佩奇和谢尔盖·布林在描述其搜索引擎原型的原始论文中使用的值。)
用计算机模拟这一过程很容易。我为此写了一个程序并运行了它,直到访问者访问了1 000个网页。(当然,这并不意味着是1 000个不重复的网页。对同一网页的多次访问也被纳入了计算当中,在这个例子中,所有网页都被访问了多次。)这1 000次模拟访问的结果显示在图17的上图中。你可以看到,网页D的访问次数最多,有144次。
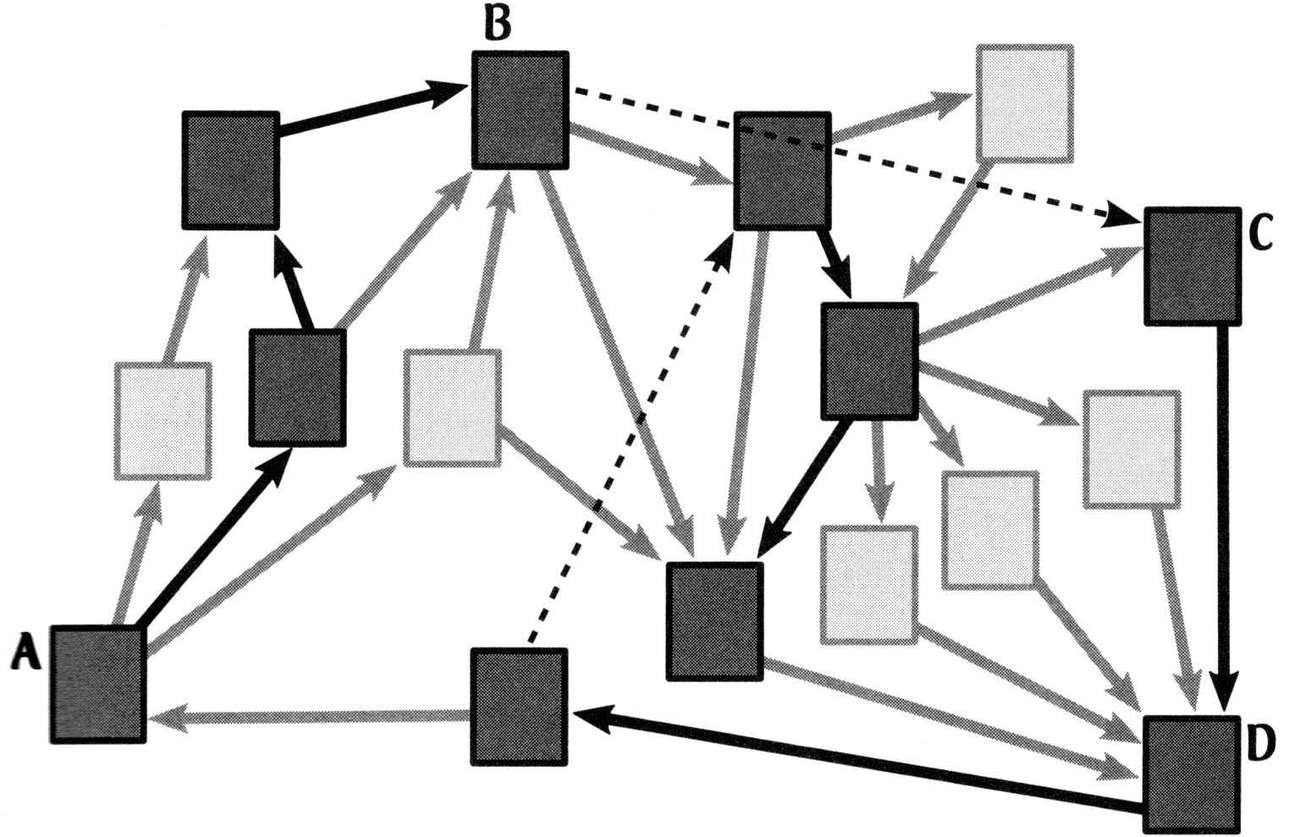
图16 随机访问者模式。被访问者访问的网页用灰色表示。虚线箭头代表随机重新开始访问(restart);实线箭头从网页A开始,指向随机选择的超链接,并被两个随机重新开始访问箭头打乱
就像民意调查一样,我们可以通过增加随机样本的数目来提高模拟精度。我重新运行了一次模拟,直到访问者访问了100万个网页。(也许你会想这花了多长时间,在我电脑上运行只花了不到半秒!)考虑到访问量如此巨大,我们还是用百分比表示结果更好。这也就是你将在图17的下图中看到的情形。和之前的结果一样,网页D的访问次数最频繁,占总访问量的15%。
随机访问者模型和权重把戏之间有什么联系可以被我们用于网页排名呢?从随机访问者模拟中计算得出的百分比,正好就是我们在衡量一个网页的权重时所需要的。因此,让我们将网页的访问者权重值(Surfer Authority Score)定义为一名随机访问者访问该网页的时间比例。值得注意的是,访问者权重值能和前两个对网页重要性进行排名的把戏配合良好。我们会逐一审视这些把戏。
首先,让我们来审视一下超链接把戏:超链接把戏的主要思想是,一个有许多链入链接的网页应该有高排名。这在随机访问者模型中也适用,因为一个有许多链入链接的网页被访问的概率较大。图17下图中的网页D就是个好例子:它有五个链入链接——比模拟中的其他网页都多——访问者权重值也最高(15%)。
其次,让我们来看看权重把戏。权重把戏的主要思想是,和来自低权重网页的链入链接相比,一个来自高权重网页的链入链接应该更能证明一个网页的排名。随机访问者模型也包含这一点。为什么?因为和一个来自不知名网页的链接相比,访问者更有可能继续点击一个来自知名网页的链入链接。要在我们的模拟中找这样一个例子,请比较图17下图中的网页A和C:这两个网页都有一个链入链接,但网页A的访问者权重值要高得多(13%对2%),这主要取决于其链入链接的质量。
注意,随机访问者模型能同时和超链接把戏及权重把戏相配合。换句话说,每个网页链入链接的质量和数量都会被纳入考虑范围。网页B就展示了这些:网页B的访问者权重值相对较高(10%),这得益于三个链入链接所在的网页拥有适中的访问者权重值,从4%到7%不等。
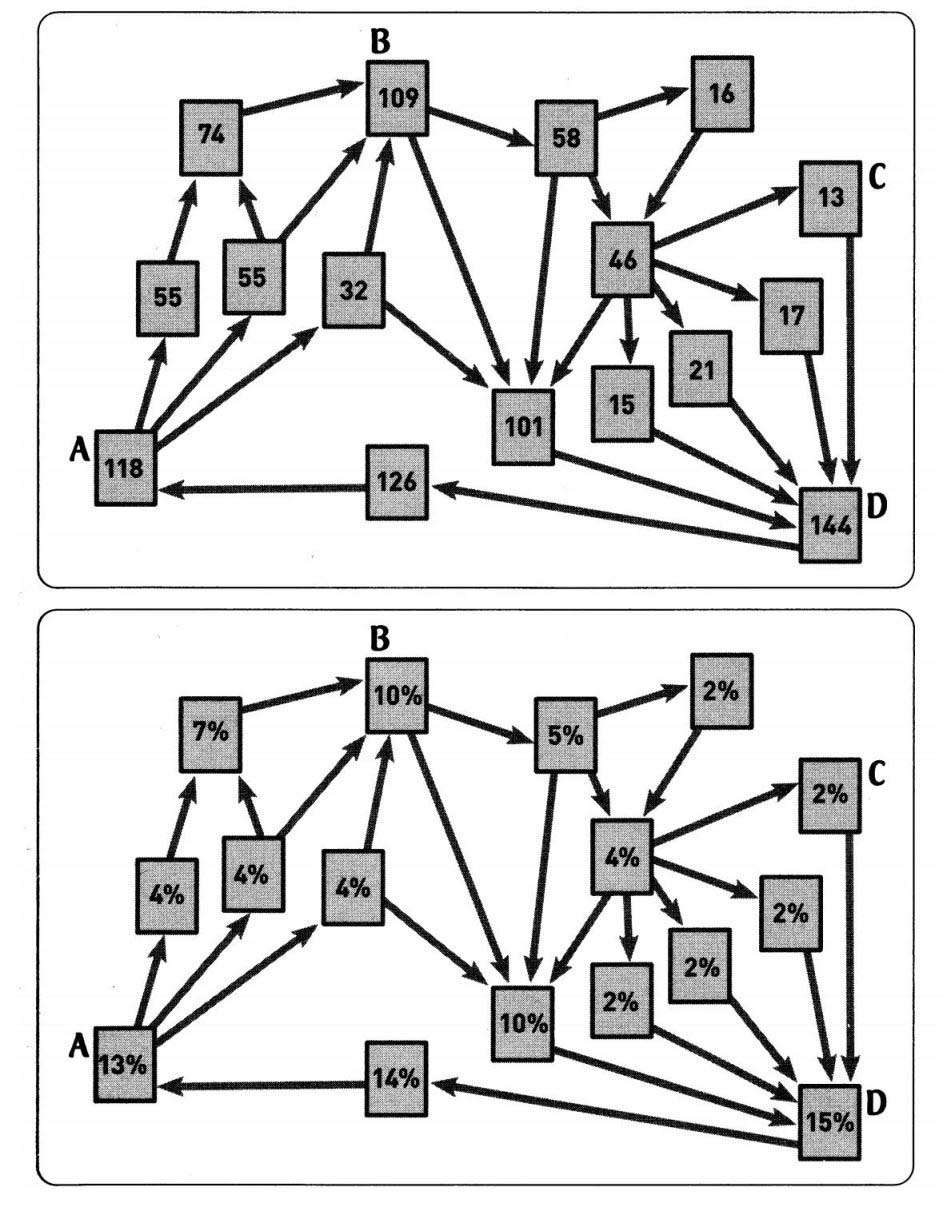
图17 随机访问者模拟。上图:1 000次访问模拟中各网页的访问次数;下图:100万次访问模拟中各网页的访问次数占比
随机访问者把戏的美妙之处在于,和权重把戏不同,不管超链接有没有形成循环,随机访问者把戏都能完美地运作。回到早前的炒蛋例子,我们能轻易地运行一次模拟随机访问。在数百万次访问之后,我的模拟产生了如下图所示的访问者权重值。请留意,和之前使用权重把戏进行的计算一样,伯特的网页访问者权重值要比欧尼的网页高很多(28%对1%)——尽管这两个网页都只有一个链入链接。因此,伯特的网页在网络搜索查询“炒蛋”中排名更高。
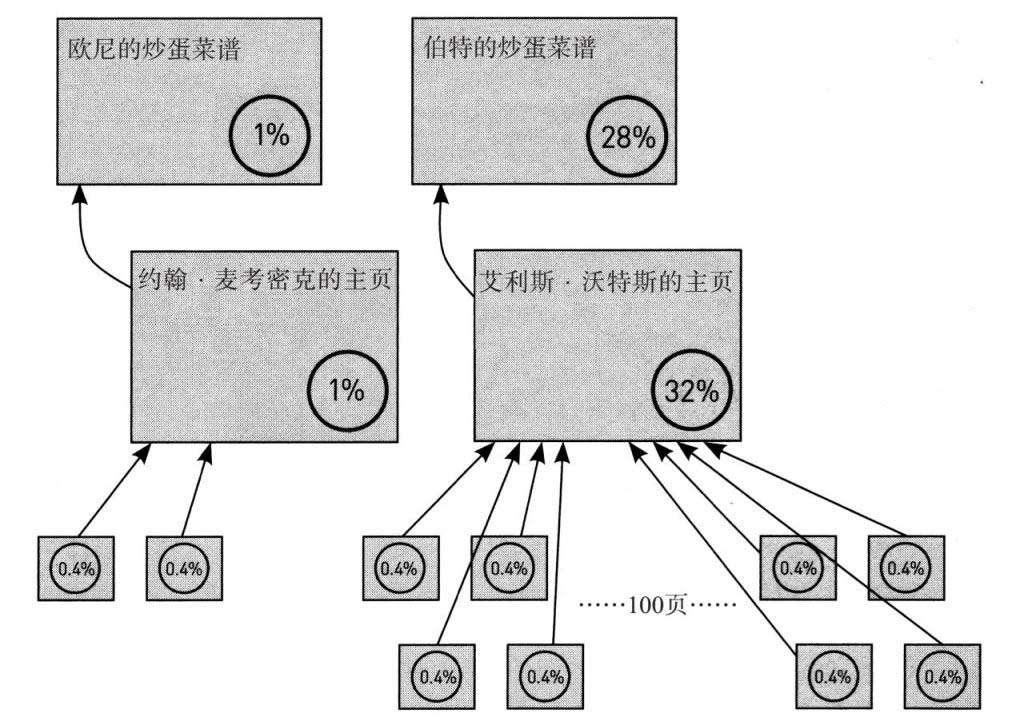
图18 前文炒蛋例子中各网页的访问者权重值。伯特的菜谱网页和欧尼的菜谱网页都只有一个链入链接传入权重,但伯特的网页在网络搜索查询“炒蛋”时排名会更高
现在让我们再转向前文中更困难的例子:对最初的权重把戏而言,由于超链接循环的存在,图14产生了一个不可解的问题。和前面一样,运行一次随机访问者的计算机模拟很容易,于是产生了如下图所示的访问者权重值。这一模拟判定的访问者权重值给出了网页的最终排名,这些排名会被搜索引擎在返回结果时使用:网页A排名最高,之后是B和E,C和D的排名同列最后一名。
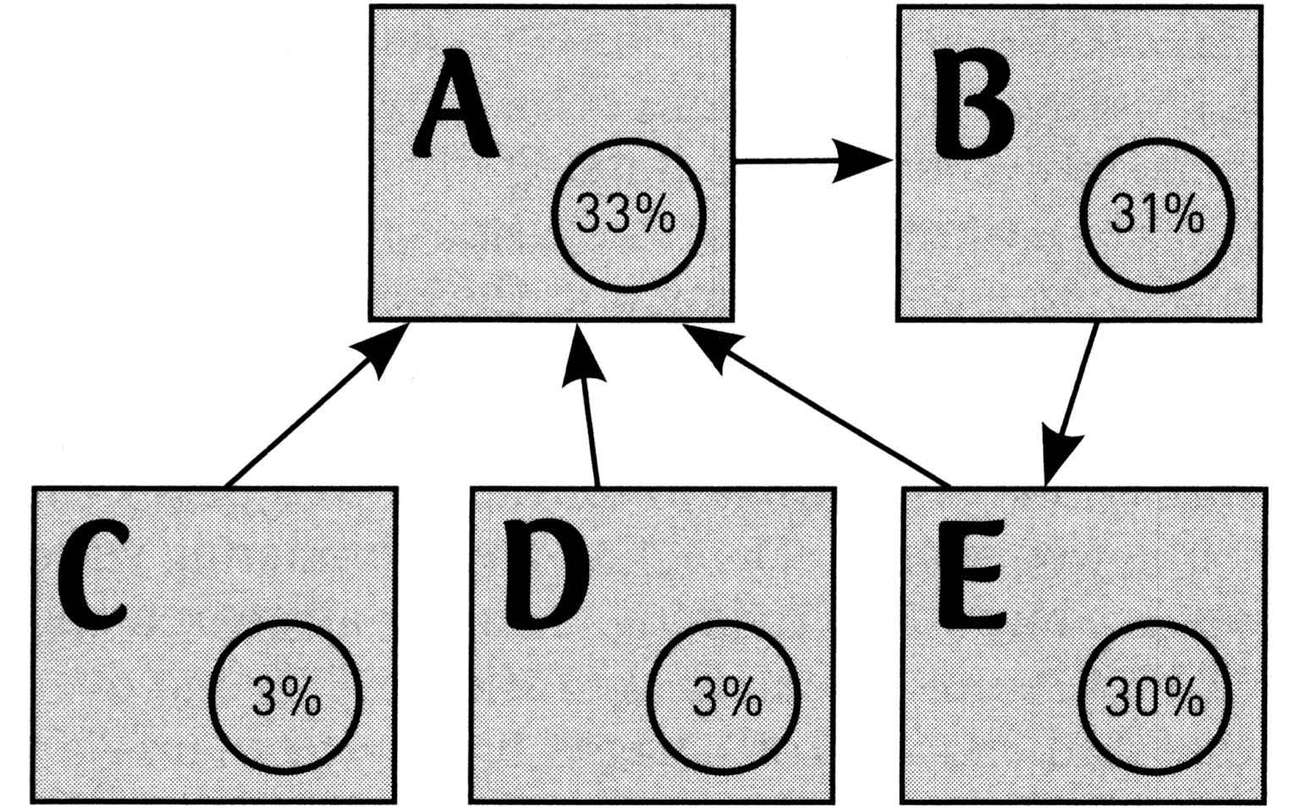
图19 早前超链接循环例子图14的访问者权重值。随机访问者把戏在计算合理的分值上没有问题,尽管存在一个循环(A→B→E→A)
实践中的PageRank
谷歌的两位联合创始人于1998年在他们著名的会议论文《解析大规模超文本网络搜索引擎》中描述了随机访问者把戏。通过和其他许多技术结合,这一把戏的变体仍被主流搜索引擎使用。不过,由于众多复杂因素,应用在现代搜索引擎中的实际技术和本章描述的随机访问者把戏略有不同。
其中一个复杂因素直击PageRank的核心:超链接传输的合法权威性假设有时存在争议。我们先前已了解到,尽管超链接能代表批评而非推荐,但这在现实中并不是个很大的问题。另一个更加严重的问题是,人们可以滥用超链接把戏,人为地提高自己网页的排名。假设你运营着一个名为BooksBooksBooks.com的网站来售书,通过使用自动化技术,创建一大堆不同的网页,并让这些网页都链接BooksBooksBooks.com,做到这一切相对很容易。因此,如果搜索引擎像本章描述的一样来计算PageRank权重,BooksBooksBooks.com的权重值就能比其他书店高很多倍,进而有更高的排名和更多的销售额,而这都不是BooksBooksBooks.com应得的。
搜索引擎称这种滥用为网络垃圾(Web Spam,这一术语是和电子邮件垃圾<e-mail spam>类比得来的:电子邮件收件箱中无用的信息,类似于充斥在搜索结果中无用的网页)。对所有搜索引擎而言,侦测并消除不同类型的网络垃圾是一直在进行的重要任务。比如,在2004年,微软的一些研究人员发现,逾30万个网页都只有1 001个网页链向它们——这是件非常令人生疑的事情。通过手动检查这些网页,研究人员发现,这些链入超链接绝大多数都是网络垃圾。
因此,搜索引擎和网络垃圾制造者在进行一场“军备竞赛”。搜索引擎不断地尝试完善算法,以便返回真实排名。在完善PageRank算法的驱动下,大量针对其他使用互联网超链接结构进行网页排名的算法的学术和行业研究应运而生。这类算法通常被称为基于链接的排名算法(Link-based Ranking Algorithms)。
另一个复杂因素与PageRank计算的高效性有关。访问者权重值是通过运行随机模拟来计算的,但在整个互联网上运行这类模拟耗时太长,所以它们不能被实际运用。因此,搜索引擎并非通过模拟随机访问者来计算PageRank值:它们使用像随机访问者模拟一样给出相同答案的数学技巧,但计算成本要低很多。我们研究访问者模拟技术是因为它直观的吸引力,也因为它描述的是搜索引擎计算什么,而非如何计算。
另外,值得一提的还有,商业搜索引擎中用来判定排名的算法要比PageRank这类基于链接的排名算法多得多。即便是在他们于1998年发表的描述谷歌的原始论文中,谷歌的联合创始人也提到了多种对搜索结果排名有贡献的功能。正如你所想的,这项技术已经进步了:在写作本书时,谷歌官网上声明“有超过200个信号”被用于评估一个网页的重要性。
除了现代搜索引擎的众多复杂性,PageRank的核心思想——权威性网页通过超链接向其他网页传输权重——仍然有效。正是这一思想帮助谷歌击败了AltaVista,让谷歌从一家小型创业企业在几年后成长为“搜索之王”。若没有PageRank的核心思想,绝大多数搜索引擎查询都将被成千上万“命中”但不相关的“网页海洋”淹没。PageRank的确是一块算法瑰宝,能让“针”毫不费力地冒到“草垛”的顶端。


