2.3 公钥密码算法
对称密码算法在密钥分配方面面临着管理和分发的困难,而且对称加密算法无法实现抗抵赖的要求,公钥密码算法的出现解决了这一难题。1976年,Diffie和Hellman首次提出了公开密钥加密算法,在密码学的发展史上具有里程碑式的意义。之后,Rivest、Shamire和Adleman提出了第一个比较完善的公钥密码算法,即著名的RSA算法。
公钥密码算法提出了“公私密钥对”的概念,这一对“互补”的密钥能够提供身份认证和抗否认等安全保障,并且使得安全的密钥交换成为可能。目前,已经出现的多数非对称密码算法所依赖的数学难题大致有:大整数因式分解、离散对数、多项式求根、背包问题、二次剩余问题和模 n 的平方根问题等。这里所说的数学难题指的是不存在一个计算该问题的有效方法,或者说在目前和以后足够长的时间里,计算该问题都是不可行的,要花很长的时间,这就大大增加了密码破译的成本。
常见的公钥密码算法有:RSA、ElGamal公钥密码算法、椭圆曲线公钥密钥算法(ECC)、NTRU公钥加密算法和Rabin公钥加密算法等。一些算法如著名的背包算法等都已经被破译,比较安全的公开密钥算法主要有:RSA及其变种Rabin算法,以及基于离散对数难题的ElGamal算法和椭圆曲线算法。
 2.3.1 公钥密码基本概念
2.3.1 公钥密码基本概念
在对称密码算法中,解密密钥与加密密钥相同或者由加密密钥可以推导出解密密钥,但在公钥密码算法中,解密密钥和加密密钥是不同的。这不仅仅体现在形式上,还体现在从其中的一个难以推导出另外一个,这就从根本上决定了公钥密码算法的加密密钥与解密密钥是可以分离的。公钥密码算法解决了密钥的管理和分发问题,每个用户都可以公开自己的公钥,并由用户自己保存私钥,不被他人获取。
公开密钥算法与对称加密算法显著的不同是用一个密钥进行加密,而用另一个不同但是相关的密钥进行解密。
A加密: X -> Y , Y = E (PuB( X )) A用B的公钥PuB对明文 X 进行加密得到 Y
B解密: Y -> X , X = D (PrB( Y )) B用自己的私钥PrB对密文 Y 进行解密获得 X
上式中, X 表示明文, Y 表示加密后的密文, E 表示加密, D 表示解密。PuB是B的公钥,该密钥是公开的,A使用此密钥加密数据传给B;P rB是B的私钥,由B保存且不能被外人所知,B使用此密钥解密A用P uB加密过的数据。P uB和P rB是相互关联的,而且是成对出现的。
公钥密码算法的另一个特性是,仅仅知道密码算法和加密密钥而想确定解密密钥,在计算上是不可能的。显然,PuB和PrB虽然相关,但是由PuB不能推导出PrB,否则将无安全性可言。
公钥密码算法大多数都是基于困难问题的。正如把盘子打碎成数千个碎片很容易,但是把所有这些碎片再拼成一个完整的盘子就很难了。类似地,将许多大素数相乘比将其乘积的结果进行因式分解要容易得多。
 2.3.2 RSA密码算法
2.3.2 RSA密码算法
在实际中,求一对大素数的乘积很容易,但要对这个乘积进行因式分解则非常困难,因此,可以把一对大素数的乘积公开作为公钥,而把素数作为私钥,从而把使用公钥将密文恢复成明文的难度等价于分解两个大素数之积。
还有基于RSA算法建立的签名算法,由于计算能力的不断提高,RSA的密钥长度也在不断提升,从512增加到1024、2048、4096。
RSA算法的密钥产生和加解密过程如下所述。其中, m 表示明文, c 和 s 表示密文。
1.密钥的产生过程
1)独立选取两个大素数 p 和 q (各为100~200位十进制数字,根据需要的密钥长度进行选择)。
2)计算 n = p ∗ q ,其欧拉函数值 ϕ ( n )=( p -1)( q -1)。
3)随机选取一个整数 e ,满足1≤ e < ϕ ( n ),并使最大公约数gcd( ϕ ( n ), e )=1。
4)在模 ϕ ( n )下,计算 e 的逆: d = e -1 mod( p -1)( q -1)。
5)以 n , e 为公钥, d 为私钥( p , q 不再需要,可以销毁)。
2. RSA算法用于加密和解密
1)加密过程: c = m e mod n 。
2)解密过程: m = c d mod n 。
3. RSA算法用于数字签名和验证
1)签名过程: s = m d mod n 。
2)验证过程: m = s e mod n 。
RSA算法的安全性是基于大整数分解的困难性假定。如果能分解 n = p ∗ q ,就可以立即获得 ϕ ( n )=( p -1)( q -1),从而计算得到 d 。
 2.3.3 椭圆曲线密码算法
2.3.3 椭圆曲线密码算法
椭圆曲线密码算法是另外一类重要的公钥密码算法,它是基于椭圆曲线上的离散对数问题。我们首先对椭圆曲线的概念及椭圆曲线中的运算做简要介绍。
1.椭圆曲线概念
所谓椭圆曲线是指由韦尔斯特拉(Weierstrass)方程
E : y 2 + axy + by = x 3 + cx 2 + dx + e
所确定的曲线,其中的参数 a , b , c , d , e 以及变量 x 和 y 都属于 F , F 是一个域,可以是有理数域、复数域或是有限域 GF ( p ),椭圆曲线是其上所有点( x , y )的集合,再加上一个无限远点。这个无限远点是椭圆曲线的一个特殊点,记为 O ,也称为无穷远点,它并不在椭圆曲线 E 上,如图2-19所示。
对椭圆曲线上的加法运算定义:设 P 和 Q 两点是椭圆曲线上的两点,通过这两点的直线与曲线交于第三点 R ,该点的 x 轴对称点 R′ 即为 P 和 Q 之和,图2-20a可以清楚地说明该过程;当 P = Q 时,则通过这点作曲线的一条切线,这条切线与曲线的交叉点 R 的 x 轴对称点 R′ 则为 P 和 Q 之和,如图2-20b所示。
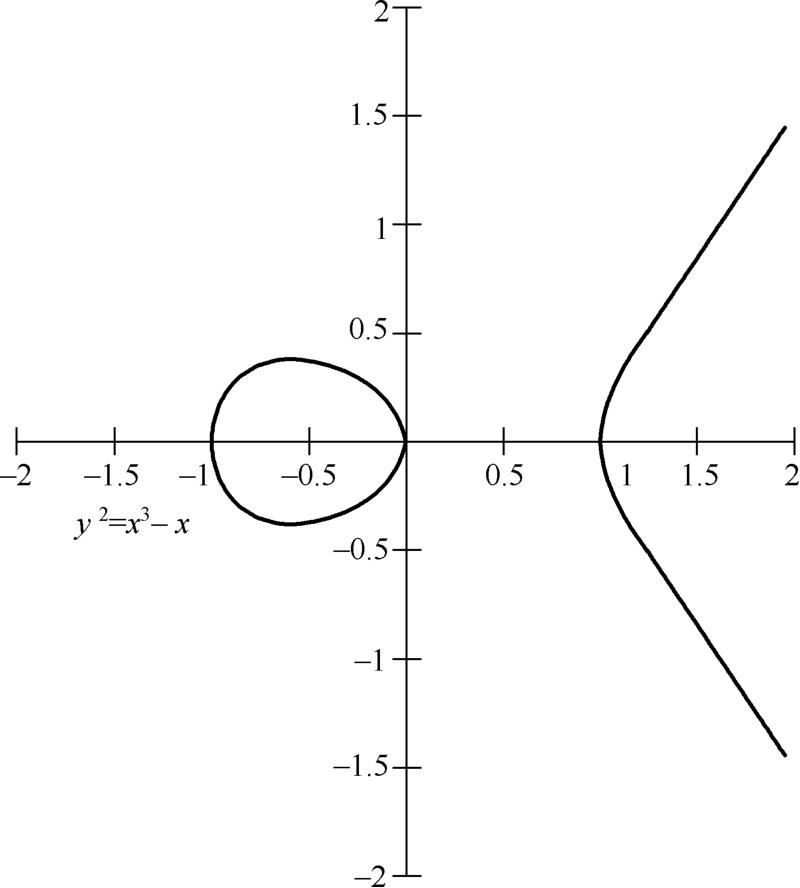
图2-19 实数域上的椭圆曲线
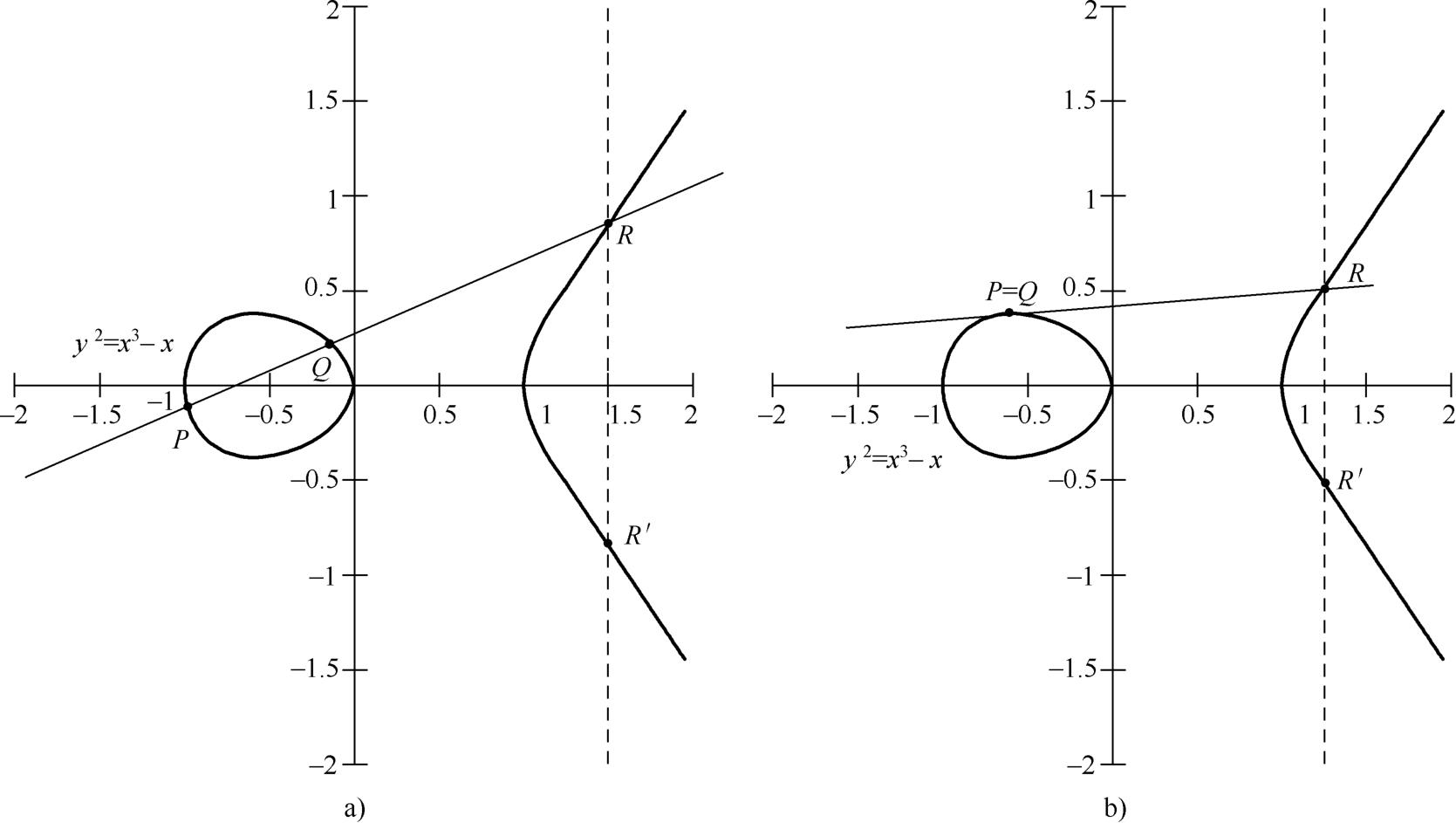
图2-20 椭圆曲线的加法运算
a) P 与 Q 为椭圆曲线上的两点时 b) P 与 Q 为同一点时
椭圆曲线的加法运算特性归纳如下。
1)封闭性:两点相加的结果是曲线上的另一点。
2)结合性:( P + Q )+ R = P +( Q + R )。
3)交换性: P + Q = Q + P 。
4)单位元素:存在加法单位元素 O ,使得 P = P + O = O + P 。
5)存在逆元素:曲线上每一点都有逆元素,其逆元素对称于 x 轴,单位元素为其本身的逆元素。
在密码学中,普遍使用有限域上的椭圆曲线,即在前面的椭圆曲线方程中,所有的系数都属于某个有限域 GF ( p )中的元素,最常用的方程为
E : y 2 = x 3 + ax + b (mod p )
其中, p 是一个大于3的素数,参数 a , b 以及变量 x 和 y 都属于有限域 GF ( p ),即从{0,1,…, p -1} 中取值,且4 a 3 +27 b 2 (mod p )≠0。该椭圆曲线包括有限个点数 N (称为椭圆曲线的阶,包括无穷远点 Ω ), N 越大,安全性越高。
定理2.3.1 椭圆曲线上的点集对于如下定义的加法规则构成一个阿贝尔(Abel)群。此加法运算的定义如下。
设 P ( x 1 , y 1 ), Q ( x 2 , y 2 )∈ E ,若 x 2 = x 1 , y 2 = -y 1 ,则 P + Q = O ;否则, P + Q =( x 3 , y 3 ),其中
x 3 = aλ 2 -x 1 -x 2 , y 3 = λ ( x 1 -x 3 ) -y 1
且
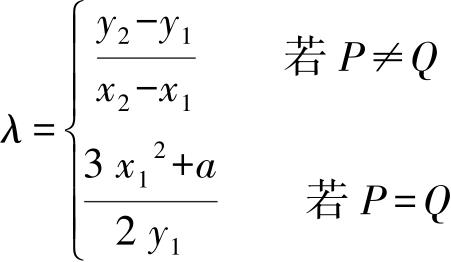
此外,对于所有的 P ∈ E 有
P + O = O + P = P
在这样一个阿贝尔群中, P 的逆元为( x 1 , -y 1 ),写作 -P 。这个阿贝尔群记作 E p ( a , b )。
椭圆曲线密码算法的重点在于一个点 P 及其在这个阿贝尔群上的 k 倍(即 kP )之间的关系。为了直观地表现出这种关系,借用实数域上的图形来对此加以解释。
图2-20b所示,2 P 所在的点为 R ,即经过 P 作一条切线,该切线与椭圆曲线相交的点沿 x 轴对称的那一点即为2 P 所在的位置。那么3 P 则为 R + P ,即连接 P 和 R 与曲线的交点关于 x 轴的对称点,依此类推可以得出 kP 。
椭圆曲线密码算法的安全性基于如下的问题。
对于给定的两个点 P 和 Q ,它们存在如下关系。
P = kQ
一个外人在拥有点 P 和 Q 的坐标的情况下,计算 k 值是困难的,这一问题被称为椭圆曲线离散对数问题(ECDLP)。ECDLP可以用穷尽查找法来求解,即已知条件点 P 和 Q ,将 P 不断自加,直至到达 Q 点。如果 k 值很大,解决这一问题就十分困难了。
在ECDLP的基础上,如何对明文、密文及密钥进行处理以使它们构成一个在模 P 上的加密系统的方法有多种,不同的方法可以构成不同的加密算法。下面给出其中的一种算法。
2.椭圆曲线密码算法
基于前面所定义的阿贝尔群,现在只给出一种椭圆曲线密码算法的描述,这里不对其有效性进行详细证明。
假设发送方为A,接收方为B,A需要将消息加密后传送给B。那么,首先需要考虑如何用椭圆曲线来生成B的公私密钥对,可以分为以下3步。
(1)构造椭圆群
设 E : y 2 = x 3 + ax + b (mod p )是 GF ( p )上的一个椭圆曲线( p >3),首先构造一个群 E p ( a , b )。
(2)挑选生成元点
挑选 E p ( a , b )中的一个生成元点 G =( x 0 , y 0 ), G 应满足使 nG = O 成立的最小的 n 是一个大素数。
(3)选择公私密钥
选择整数 k B ( k < n )作为私钥,然后产生其公钥 P B = k B G ,则B的公钥为( E , n , G , P B ),私钥为 k B 。
下面介绍如何利用公私密钥对进行加解密的运算(以下的运算都是在mod p 下进行的)。
(1)加密过程
1)发送方A将明文消息编码成一个数 m < p ,并在椭圆群 E p ( a , b )中选择一点 P t =( x t , y t )。
2)发送方A计算密文: C = mx t + y t 。
3)发送方A选取一个保密的随机数 r (0< r < n ),并计算 rG 。
4)依据接收方B的公钥 P B ,计算 P t + rP B 。
5)发送方A对 m 进行加密,得到数据 C m ={ rG , P t + rP B , C }。
(2)解密过程
接收方B在收到A发来的加密数 C m ={ rG , P t + rP B , C }之后,进行如下操作。
1)使用自己的私钥 k B 计算
P t + rP B -k B ( rG )= P t + r ( k B G ) -k B ( rG )= P t
2)接收方B计算: m =( C-y t )/ x t ,得到明文 m 。
从上面的描述可以看出,如果攻击者想从密文 C 得到明文 m ,就必须知道 r 或 k B ,但是,已知 rG 或 P B 求得 r 或 k B ,都必须去解决椭圆曲线上的离散对数问题。因此,在现有的计算条件下,椭圆曲线密码算法是安全的。与其他算法相比较,椭圆曲线密码具有两个优点:一是算法的密钥长度短,对于带宽和存储的要求比较低,运算效率高,适合在智能卡等计算与存储资源都有限的硬件设备上使用;二是所有用户可以选择使用同一基域 F 上的不同曲线 E ,从而可以让所有用户使用相同的硬件来完成域算术。
3.椭圆曲线密码算法的安全性
相对于基于有限域乘法群上的离散对数问题的密码算法,椭圆曲线密码算法的安全性是基于椭圆曲线上的离散对数问题,目前这一方法还没有发现明显的弱点,但也有一些这方面的研究思路,如利用一般曲线离散对数的攻击方法以及针对特殊曲线的攻击方法等。
为了保证椭圆曲线密码算法的安全性,就需要选取安全的椭圆曲线。用于建立密码算法的椭圆曲线的主要参数有 p 、 a 、 b 、 G 、 n 和 h ,其中 p 是域的大小,取值为素数或2的幂; a 、 b 是方程的系数,取值于 GF ( p ); G 为生成元点; n 为点 G 的阶;还定义了参数 h 为椭圆曲线上所有点的个数 N 除以 n 所得的结果。为了较好地建立一个椭圆曲线算法,需要大致满足如下几个条件。
1) p 的取值应尽可能大,但数值越大,计算时所消耗的时间也越多,为满足目前的安全要求, p 的位数可为160位。
2) n 为大素数,并且应尽可能大。
3)4 a 3 +27 b 2 ≠0(mod p )。
4)为保证 n 的取值足够大,需满足 h ≤4。
5)不能选取超奇异椭圆曲线和异常椭圆曲线这两类特殊的椭圆曲线。
由于椭圆曲线的离散对数问题被公认为比整数的因式分解以及有限域的离散对数问题还要困难得多。因此,对于它的密钥长度的要求可以大大降低,这也是该算法能够高效运行的一个原因。通常而言,160位的椭圆曲线密钥的安全强度就能达到1024位RSA算法的安全强度,这也使其成为目前已知的公钥密码算法中安全强度最高的算法之一。
 2.3.4 NTRU公钥密码
2.3.4 NTRU公钥密码
传统公钥算法在无线通信安全领域的使用还不是很广泛,主要原因是移动终端上的计算和存储资源的限制,使得这些算法在移动终端上的运行速度难以满足某些应用的要求。因此,对快速公钥系统的研究是当前公钥系统研究的一个热点。
1. NTRU概述
NTRU(Number Theory Research Unit)是一种基于多项式环的加密系统,其加解密过程是基于环上多项式代数运算和对数 p 及 q 的模约化运算,只使用了简单的模乘法和模求逆运算,因此它的加解密速度快,密钥生成速度也快,而且NTRU是迄今为止唯一的增加格的维数而不损害其实用性的格密码算法。它很好地解决了公钥密码算法的最大瓶颈——速度问题,使其适用于安全性要求、体积、成本、内存及计算能力等受限的电子设备。近年来,NTRU算法引起了许多密码学家的讨论,它是目前为止已知的速度最快的公钥密码算法之一。
NTRU是1995年由J. Hoffstein、J. Pipher和J. Silverman发明的一种密码算法。在数学上,NTRU比RSA和ElGamal密码还要复杂。由于它的复杂性和出现的时间相对较短,国内外密码学界针对NTRU的安全性研究仍在继续。NTRU也存在一些缺点,比如它虽然能够实现概率加密却存在解密失败的问题,虽然人们对它进行了改进,然而这也大大损伤了该算法的简洁性。另外,与RSA和ECC算法相比,NTRU算法需要更大的带宽和更大的密钥空间。例如,对应于公钥长度为1024位的RSA算法,NTRU的公钥长度是RSA的两倍。但是,这种差异会随着安全级别的增大而降低。
虽然密码学界对NTRU进行了各种各样的攻击,但是这些都没有对它造成致命的威胁。据密码学家表示,只有当量子计算机得到应用时,NTRU密码算法才有可能被破解,而那时RSA和普通的ElGamal密码已经被破解了。
2. NTRU的理论基础
Diffie和Hellman提出应利用计算的复杂性来设计加密算法,并指出可利用格理论以及NP C问题构造密码系统。此后的各种公钥系统设计均遵循这一原则,而NTRU算法正是基于格理论在密码学上的重要应用。
格在不同的领域有不同的定义。在代数系统中,格通常定义为:设< L ,≤>是一个偏序集,如果对任意 a , b ∈ L ,{ a , b }都有最大下界和最小上界存在,则称< L ,≤>是格,这时< L ,≤>可简写成 L 。
而NTRU系统中所涉及的格的概念不同于上述的代数格,而是一个定义在 n 维欧式空间上的离散子群。设 R m 是一个 m 维的欧式空间,则 R m ( m ≥ n )是由 n 个线性无关的向量 a 1 , a 2 ,…, a m 的所有整数线性组合的集合。
L ( a 1 , a 2 ,…, a m )={∑ x i a i : x i ∈ Z }构成了 R m 的一个格。B=( a 1 , a 2 ,…, a m )称为格 L 的一组基,维数为 m ,秩为 n 。若 m = n 则称格 L ( a 1 , a 2 ,…, a m )是满维的。
简单来说,NTRU是基于高维格中寻找一个短向量的困难问题(SVP),即给定一个多项式 h ( x )= F q ∗ g ( x )(mod q ),其中 F q 是多项式 f ( x )在模 q 时的逆元, f ( x )和 g ( x )的系数相对于 q 来说是小的,在适当参数设置下,如果仅知道 h ( x ),恢复出多项式 f ( x )或 g ( x )是困难的。
3. NTRU算法描述
NTRU密码算法的工作过程如下。
(1)密钥生成
在NTRU公钥密码算法中,接收方需要生成一组公/私密钥对。具体步骤如下:
1)选择公开参数。选择正整数参数 N 、 p 、 q ,其中 p 、 q 不必为素数,但是它们必须互素,且满足gcd( N , pq )=1。
2)选择多项式 f ( x )和 g ( x )。由接收方选择两个小系数多项式 f ( x )和 g ( x ),其中模 q 的随机多项式的系数一般随机地分布在区间[0, q ]上,而所谓的小系数多项式的系数相对于模 q 的随机多项式要小得多。接收方需要对多项式 f ( x )和 g ( x )保密,因为任何一个多项式信息泄露都可能导致密文被破解。
3)计算逆元 F p ( x )和 F q ( x )。接收方计算多项式 f ( x )在模 p 和模 q 时的逆元 F p ( x )和 F q ( x ),即 F p ( x )∗ f ( x )=1(mod p ,mod x N -1)和 F q ( x )∗ f ( x )=1(mod q ,mod x N -1)。如果 f ( x )的逆元不存在,接收方需要重新选取 f ( x )。
4)计算公钥。计算 h ( x )= F q ( x )∗ g ( x )(mod q ,mod x N -1),多项式 f ( x )和 F p ( x )为私钥, h ( x )为公钥。
(2)加密过程
假设发送者发送一条明文消息 m ( x )给接收者, m ( x )是次数为 N -1的多项式,具有模 p 约简的系数(可以理解为系数的范围在( -p /2, p /2)内)。发送方随机选择一个次数为 N -1的多项式 r ( x )进行计算得到
c ( x )= pr ( x )∗ h ( x )+ m ( x )(mod q ,mod x N -1)
然后将其发送给接收方。
(3)解密过程
假设接收者收到加密消息 c ,首先计算多项式 a ( x )
a ( x )= f ( x )∗ c ( x )(mod q ,mod x N -1)
接着计算
d ( c )= F p ( x )∗ a ( x )(mod p ,mod x N -1)
d ( c )就是解密后的明文。
(4)说明
这里的加法+,是通常的多项式加法。这里的乘法∗,是比较特殊的乘法。设R为关于 x 的多项式的集合,具有整数系数和严格比 N 小的次数,乘法∗表示
x i ∗ x j = x i + j (mod N )
也就是
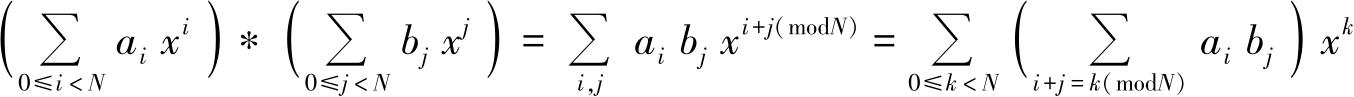
该乘法依然满足交换律、结合律和分配律。此外,算法还会涉及模 p 约简和模 q 约简运算,这是指分别对多项式的系数做模 p 或 q 的约简。可以写作
f ( x )(mod p )=系数经过模 p 约简的多项式 f ( x )
f ( x )(mod q )=系数经过模 q 约简的多项式 f ( x )
(5)解密原理
因为 a ( x )= f ( x )∗ c ( x )(mod q ,mod x N -1)
= f ( x )∗( pr ( x )∗ h ( x )+ m ( x ))(mod q ,mod x N -1)
= f ( x )∗( pr ( x )∗ F q (x)∗ g ( x )+ m ( x ))(mod q ,mod x N -1)
= f ( x )∗ pr ( x )∗ F q ( x )∗ g ( x )+ f ( x )∗ m ( x ))(mod q ,mod x N -1)
= f ( x )∗ F q (x)∗ pr ( x )∗ g ( x )+ f ( x )∗ m ( x ))(mod q ,mod x N -1)
=1∗ pr ( x )∗ g ( x )+ f ( x )∗ m ( x ))(mod q ,mod x N -1)
= pr ( x )∗ g ( x )+ f ( x )∗ m ( x ))(mod q ,mod x N -1)
考虑到多项式 pr ( x )∗ g ( x )+ f ( x )∗ m ( x ),只要参数选取适当,几乎可以确保多项式 pr ( x )∗ g ( x )+ f ( x )∗ m ( x )每一项的系数都在( -q /2, q /2)区间上,即
a ( x )= pr ( x )∗ g ( x )+ f ( x )∗ m ( x )(mod x N -1)
将 a ( x )再mod p 得到
a ( x )= f ( x )∗ m ( x )(mod p ,mod x N -1)
则解密操作后可以得到
d ( c )= F p ( x )∗ a ( x )(mod p ,mod x N -1)
= F p ( x )∗ f ( x )∗ m ( x )(mod p ,mod x N -1)
=1∗ m ( x )(mod p ,mod x N -1)
= m ( x )


