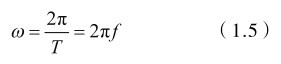1.4 正弦波信号

电子电路中的信号可分为直流信号与交流信号两类。交流信号又可分为正弦波信号与非正弦波信号两大类。非正弦波信号包括方波、矩形波、三角波、锯齿波等。模拟电路系统中主要是正弦波信号。
 1.4.1 周期与频率
1.4.1 周期与频率
正弦交流信号的大小与方向随时间的变化而作周期性的变化。工程上用的一般都是正弦交流电,即交流电的变化规律按正弦函数规律变化,如图1.17所示。正弦交流电完成一次周期性变化所需要的时间称为周期,通常用字母T 表示。
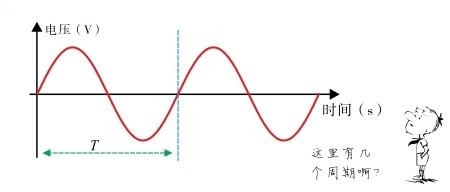
图1.17 正弦交流电
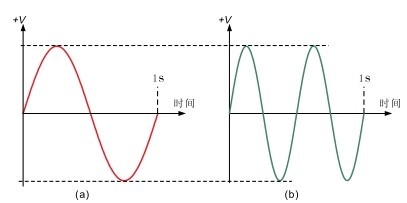
图1.18 频率
频率是指单位时间内(1s)信号发生周期性变化的次数,用字母 F 或 f 表示,如图1.18所示。频率的国际单位是赫兹(Hz)。若信号在单位时间(1s)内只周期性变化一次,则信号的频率为1Hz。
若信号在单位时间内只周期性变化两次,则信号的频率为2Hz。
频率 f 与周期 T 互为倒数的关系式(1.1),即频率越高,周期越短;频率是越低,周期越长。国内电力系统提供的交流电的频率是 50Hz,即它在 1 s内会周期性变化 50 次。因为流过灯泡的电流的变化速度极快,所以我们感觉不到它闪烁。
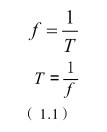
 1.4.2 正弦波的电压值
1.4.2 正弦波的电压值
正弦波有不同的电压值表述,在讲正弦波的电压值时,应了解是什么电压值。
峰值(Peak):通常又称为最大值,是正弦交流信号电压在一个周期内能达到的最大数值,可以用来表示交流电的电压高低或交流电流的强弱,常用V p 或V max 、U m 表示最大电压值,用I p 或I max 、I m 表示最大电流值。峰值对于正弦波而言,可用图1.19 表述。注意峰值与峰峰值的区别。
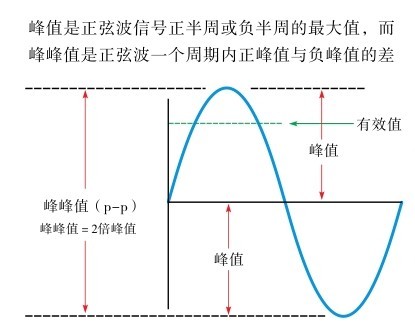
图1.19 峰值与峰峰值
有效值:
在研究交流电的功率时,最大值不够方便,它不适合用来标识交流电产生的效果。在实际工作中通常用有效值来标识交流电的大小。交流电的有效值是根据电流的热效应来规定的。让交流电与直流电通过同样阻值的电阻,如果它们在同一时间内产生的热量相等,就把这一直流电的数值叫做这一交流电的有效值。有效值通常又称为均方根值,用 RMS 表示。有效值与峰值之间的关系可用式(1.2)表述。

 1.4.3 相位与相位差
1.4.3 相位与相位差
利用电压能说明正弦波的幅度,频率或周期可以说明正弦波完成一周的变化的频繁程度。但频率相同的两个正弦波信号可能在同一时刻不在零点相交。
交流电瞬时值何时最大,何时为零,不是简单地由时间 t 来确定的,还与交流电的相位相关。因此,通过正弦波的相位可确定它们在时间轴上的位置。相位的单位为度(°),正弦波一周的相位分成 360°。两个同频率正弦量相位之差称为相位差。

图1.20 两个同相的交流电波形

图1.21 两个不同相的交流电波形
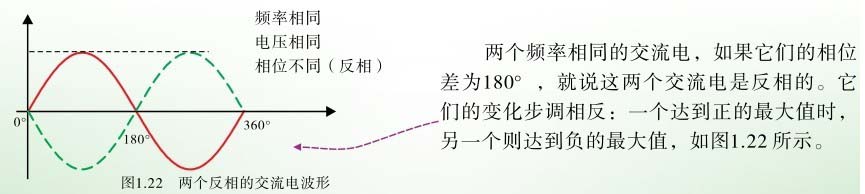
图1.22 两个反相的交流电波形
由前面的内容可以看到,正弦波信号在不同的时间点,或者说不同相位时的瞬时电压值是不同的,可用式(1.3)来估算,其中的sin∠θ为正弦波相位的正弦值。图1.23所示就是一个正弦波信号在不同相位时的瞬时电压值示例。
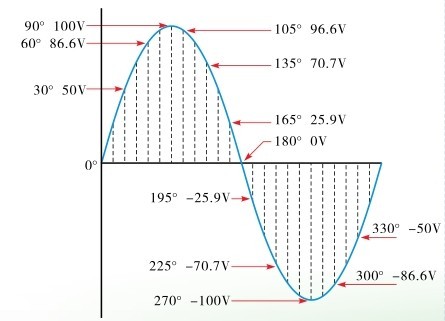
图1.23 正流波信号的不同瞬时位
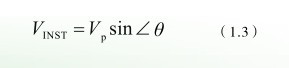
 1.4.4 角度与弧度
1.4.4 角度与弧度
前面讲正弦波转动 90°、180°,这是以角度为单位。在关于正弦交流电路的分析中,常常会看到“π”,这里有必要了解一下。
° 与π是角的两种不同度量单位,° 是角度制,π是弧度制。两者可按式(1.4)相互换算。
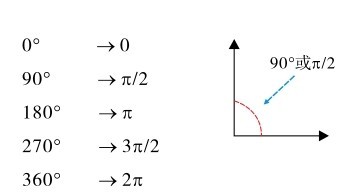

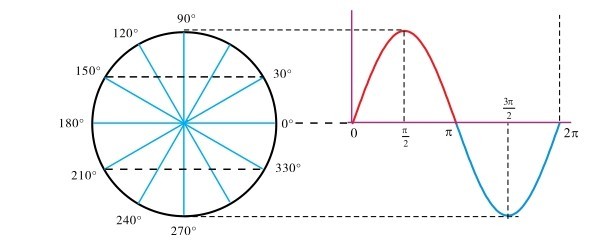
图1.24 角度与弧度
因此,有时会在平面坐标的横轴上看到以弧度标注的刻度,如图1.24中的π、2π 等。
除了用周期、频率表示交流电变化的快慢外,还可用角频率来表示交流电变化的快慢。从前面的知识可知,正弦交流电变化一周可用 360° 或 2π来计量。那么,交流电每秒钟变化的角度就叫做交流电的角频率。角频率标识为希腊字母ω,读作 Omega。
角频率ω的单位是 rad/s(弧度/秒)。角频率与周期、频率之间的关系可用式(1.5)来表达。