1.1 电路分析的基本方法与规律
学好电子电路的关键是学会分析电路,而分析电路先要掌握一些与电路分析有关的基本定律和方法。
1.1.1 欧姆定律
欧姆定律是电子技术中的一个最基本的定律,它反映了电路中电阻、电流和电压之间的关系。欧姆定律分为部分电路欧姆定律和全电路欧姆定律。
1.部分电路欧姆定律
部分电路欧姆定律内容是:在电路中,流过导体的电流 I 的大小与导体两端的电压 U 成 正比,与导体的电阻 R 成反比。 即
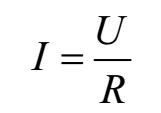
也可以表示为
U
=
IR
或
 。
。
为了让大家更好地理解欧姆定律,下面以图1-1为例来说明。

图1-1 欧姆定律的几种形式
如图1-1(a)所示,已知电阻
R
=10Ω,电阻两端电压
U
AB
=5V,那么流过电阻的电流
 。
。
又如图1-1(b)所示,已知电阻 R =5Ω,流过电阻的电流 I =2A,那么电阻两端的电压 U AB = IR =(2×5)V=10V。
在图1-1(c)中,流过电阻的电流
1
=2A,电阻两端的电压
U
AB
=12V,那么电阻的大小
 。
。
下面再来说明欧姆定律在实际电路中的应用,如图1-2所示。
在图1-2中,电源的电动势 E =12V,A、D之间的电压 U AD 与电动势 E 相等,三个电阻器R 1 、R 2 、R 3 串接起来,可以相当于一个电阻器R, R = R 1 + R 2 + R 3 =(2+7+3)Ω=12Ω。知道了电阻的大小和电阻器两端的电压,就可以求出流过电阻器的电流 I ,即
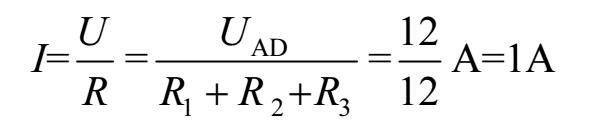
求出了流过R
1
、R
2
、R
3
的电流
I
,并且它们的电阻大小已知,就可以求R
1
、R
2
、R
3
两端的电压
 实际就是A、B两点之间的电压
U
AB
)、
实际就是A、B两点之间的电压
U
AB
)、
 (实际就是
U
BC
)和
(实际就是
U
BC
)和
 (实际就是
U
CD
),即
(实际就是
U
CD
),即
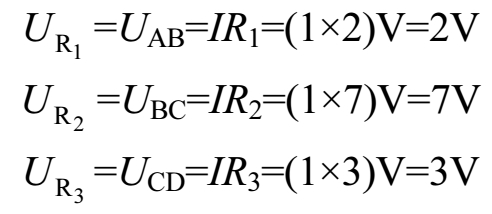
从上面可以看出:
 U
AB
+
U
BC
+
U
CD
=
U
AD
=12V。
U
AB
+
U
BC
+
U
CD
=
U
AD
=12V。
在图1-2中如何求B点电位呢?首先要明白,求 某点电位指的就是求该点与地之间的电 压, 所以B点电位 U B (习惯上称为电压 U B )实际就是电压 U BD ,求 U B 有以下两种方法。
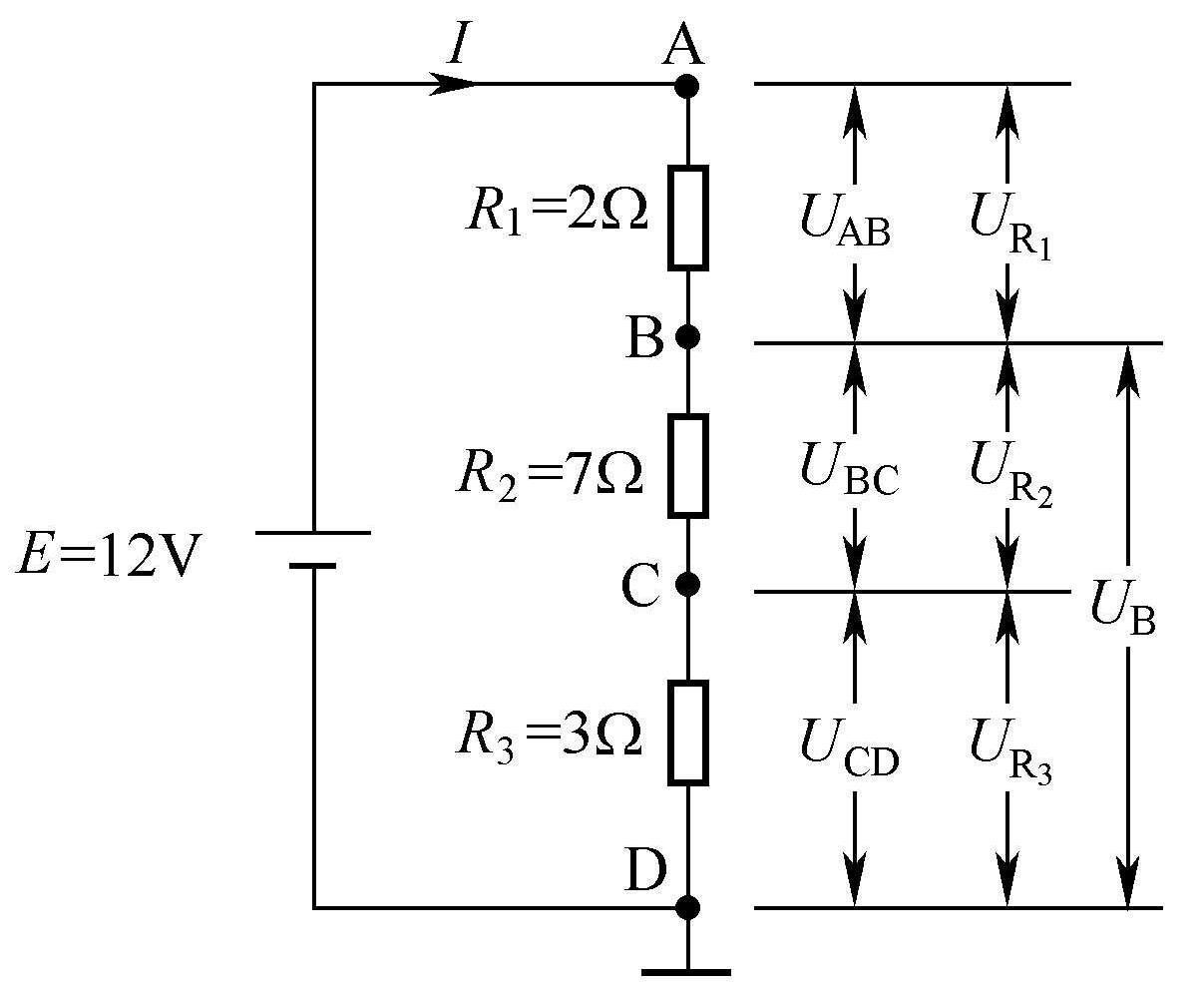
图1-2 部分欧姆定律的应用说明图
方法一: U B = U BD = U BC + U CD = U R2 + U R3 =(7+3)V=10V。
方法二: U B = U BD = U AD - U AB = U AD - U R1 =(12-2)V=10V。
2.全电路欧姆定律
全电路是指含有电源和负载的闭合回路。 全电路欧姆定律又称闭合电路欧姆定律,其内 容是:闭合电路中的电流与电源的电动势成正比,与电路的内、外电阻之和成反比, 即
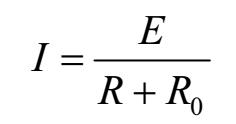
全电路欧姆定律应用说明图如图1-3所示。
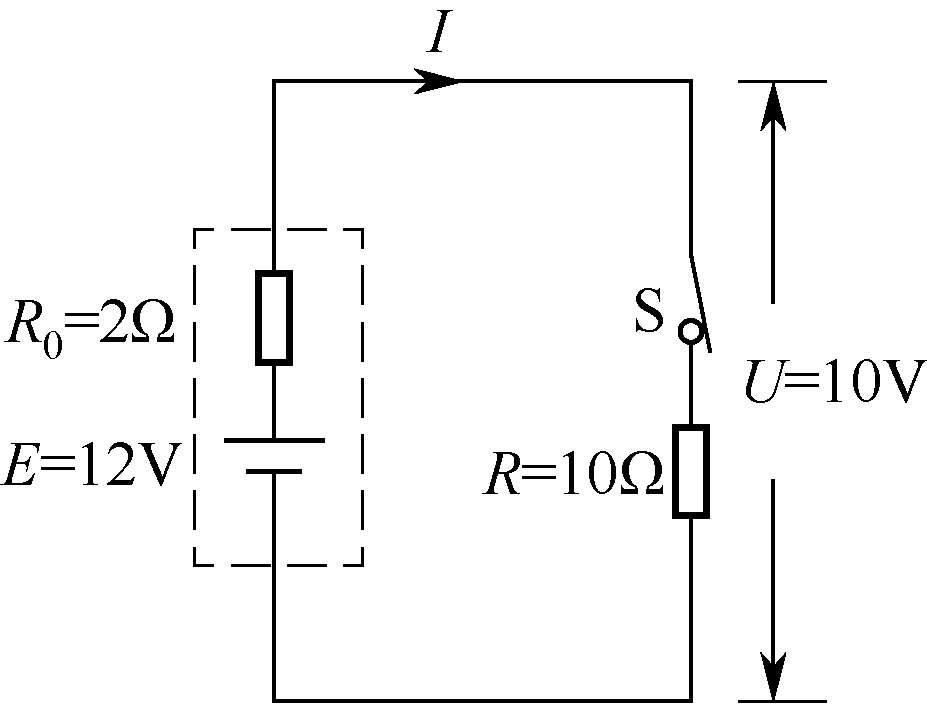
图1-3 全电路欧姆定律应用说明图
图中虚线框内为电源,R
0
表示电源的内阻,
E
表示电源的电动势,当开关S闭合后,电路中有电流
I
流过,根据全电路欧姆定律可求得
 。电源输出电压(也即电阻R两端的电压)
U
=
IR
=(1×10)V=10V,内阻R
0
两端的电压
U
0
=
IR
0
=(1×2)V=2V。如果将开关S断开,电路中的电流
I
=0,那么内阻R
0
上消耗的电压
U
0
=0V,电源输出电压
U
与电源电动势相等,即
U
=
E
=12V。
。电源输出电压(也即电阻R两端的电压)
U
=
IR
=(1×10)V=10V,内阻R
0
两端的电压
U
0
=
IR
0
=(1×2)V=2V。如果将开关S断开,电路中的电流
I
=0,那么内阻R
0
上消耗的电压
U
0
=0V,电源输出电压
U
与电源电动势相等,即
U
=
E
=12V。
根据全电路欧姆定律不难看出:
① 当电源未接负载时,不管电源内阻多大,内阻消耗的电压始终为0,电源两端电压与电动势相等。
② 当电源与负载构成闭合电路后,由于有电流流过内阻,内阻会消耗电压,从而使电源输出电压降低。内阻越大,内阻消耗的电压越大,电源输出电压越低。
③ 在电源内阻不变的情况下,如果外阻越小,电路中的电流越大,则内阻消耗的电压也越大,电源输出电压也会降低。
由于正常电源的内阻很小,内阻消耗的电压很低,故一般情况下可认为电源的输出电压与电源电动势相等。
利用全电路欧姆定律可以解释很多现象。比如旧电池两端电压与正常电压相同,但将旧电池与电路连接后,除了输出电流很小外,电池的输出电压也会急剧下降,这是因为旧电池内阻变大的缘故;又如将电源正、负极直接短路时,电源会发热甚至烧坏,这是因为短路时流过电源内阻的电流很大,内阻消耗的电压与电源电动势相等,大量的电能在电源内阻上消耗并转换成热能,故电源会发热。
1.1.2 电功、电功率和焦耳定律
1.电功
电流流过灯泡,灯泡会发光;电流流过电炉丝,电炉丝会发热;电流流过电动机,电动机会运转。由此可以看出, 电流流过一些用电设备时是会做功的,电流做的功称为电功。用 电设备做功的大小不但与加到用电设备两端的电压及流过的电流有关,还与通电时间长短有 关。 电功可用下面的公式计算:
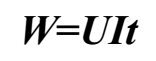
式中, W 表示电功,单位是焦 [ 耳] ( J ); U 表示电压,单位是伏[特](V); 1 表示电流,单位是安[培](A); t 表示时间,单位是秒(s)。
电功的单位是焦 [ 耳 ] ( J ),在电学中还常用到另一个单位:千瓦时( kWh ),也称度, 1千瓦时=1度。千瓦时与焦耳之间的关系是:
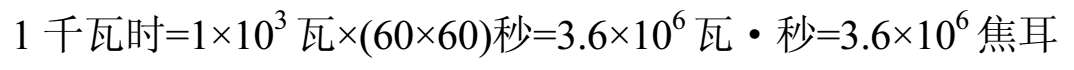
1千瓦时可以这样理解:一个电功率为100W的灯泡连续使用10个小时,消耗的电功为1千瓦时(即消耗1度电)。
2.电功率
电流需要通过一些用电设备才能做功,为了衡量这些设备做功能力的大小,引入一个电功率的概念。 电流单位时间做的功称为电功率。电功率常用 P 表示,单位是瓦 [ 特 ] ( W ), 此外还有千瓦(kW)和毫瓦(mW),它们之间的关系是:
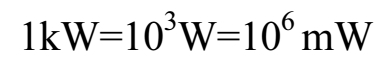
电功率的计算公式是:
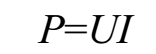
根据欧姆定律可知 U = IR , I = U / R ,所以电功率还可以用公式 P = I 2 R 和 P = U 2 / R 来求。
下面以图1-4所示电路来说明电功率计算。
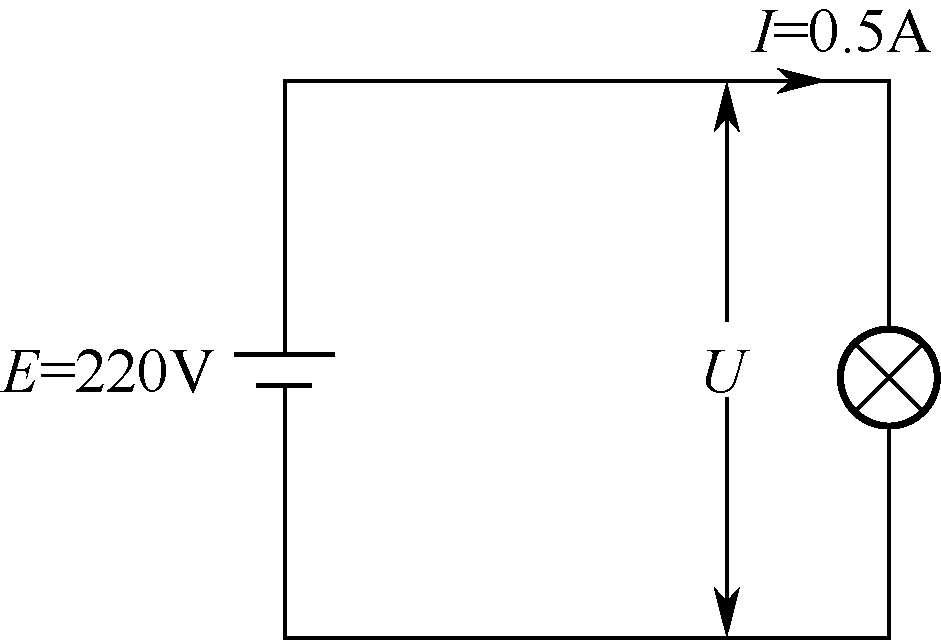
图1-4 电功率计算说明图
在图1-4电路中,灯泡两端的电压为220V(它与电源的电动势相等),流过灯泡的电流为0.5A,求灯泡的功率、电阻和灯泡在10秒所做的功。
灯泡的功率: P = UI =220V×0.5A=110VA=110W
灯泡的电阻: R = U / I =220V/0.5A=440V/A=440Ω
灯泡在10秒做的功: W = UIt =220V×0.5A×10s=1100J
3.焦耳定律
电流流过导体时导体会发热,这种现象称为电流的热效应。电热锅、电饭煲和电热水器等都是利用电流的热效应来工作的。
英国物理学家焦耳通过实验发现: 电流流过导体,导体发出的热量与导体流过的电流、 导体的电阻和通电的时间有关。 这个关系用公式表示就是:
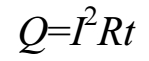
式中, Q 表示热量,单位是焦 [ 耳 ] ( J ) ; R 表示电阻,单位是欧[姆](Ω); t 表示时间,单位是秒(s)。
焦耳定律说明:电流流过导体产生的热量,与电流的平方及导体的电阻成正比,与通电 时间也成正比。 由于这个定律除了由焦耳发现外,俄国科学家楞次也通过实验独立发现,故该定律又称焦耳-楞次定律。
举例:某台电动机额定电压是220V,线圈的电阻为0.4Ω,当电动机接220V的电压时,流过的电流是3A,求电动机的功率和线圈每秒发出的热量。
电动机的功率是: P = UI =220V×3A=660W
电动机线圈每秒发出的热量: Q = I 2 Rt =(3A) 2 ×0.4Ω×1s=3.6J
1.1.3 电阻的串联、并联与混联
电阻的连接有串联、并联和混联三种方式。
1.电阻的串联
两个或两个以上的电阻头尾相连串接在电路中,称为电阻的串联, 如图1-5所示。
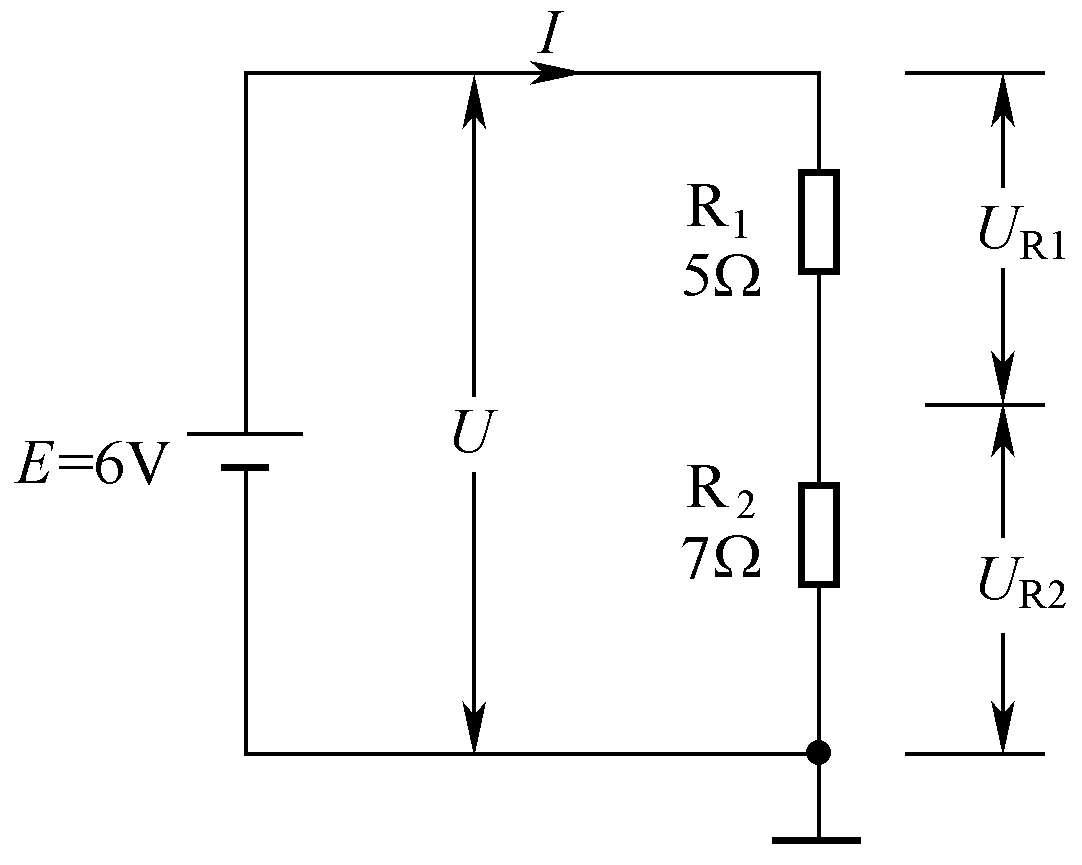
图1-5 电阻的串联
电阻串联电路的特点有:
① 流过各串联电阻的电流相等,都为 I 。
② 电阻串联后的总电阻 R 增大,总电阻等于各串联电阻之和, 即 R = R 1 + R 2 。
③ 总电压 U 等于各串联电阻上电压之和, 即 U = U R1 + U R2 。
④ 串联电阻越大,两端电压越高,
因为
R
1
<
R
2
,所以
 。
。
在图1-5所示的电路中,两个串联电阻上的总电压
U
等于电源电动势,即
U
=
E
=6V;电阻串联后总电阻
R
=
R
1
+
R
2
=12Ω;流过各电阻的电流
 ;电阻R
1
上的电压
;电阻R
1
上的电压
 =
IR
1
=(0.5×5)V=2.5V,电阻R
2
上的电压
=
IR
1
=(0.5×5)V=2.5V,电阻R
2
上的电压
 =
IR
2
=(0.5×7)V=3.5V。
=
IR
2
=(0.5×7)V=3.5V。
2.电阻的并联
两个或两个以上的电阻头尾相并接在电路中,称为电阻的并联, 如图1-6所示。
电阻并联电路的特点有:
① 并联的电阻两端的电压相等,
即
 。
。
② 总电流等于流过各个并联电阻的电流之和, 即 I = I 1 + I 2 。
③ 电阻并联总电阻减小,总电阻的倒数等于各并联电阻的倒数之和,
即
 。该式可变形为
。该式可变形为
 。
。
④ 在并联电路中,电阻越小,流过的电流越大, 因为 R 1 < R 2 ,所以流过R 1 的电流 I 1 大于流过R 2 的电流 I 2 。
在图1-6电路中,并联的电阻R
1
、R
2
两端的电压相等,
 ;流过R
1
的电流
;流过R
1
的电流
 流过A2的电流
流过A2的电流
 总电流
总电流
 R
1
、R
2
并联总电阻为
R
1
、R
2
并联总电阻为
 。
。
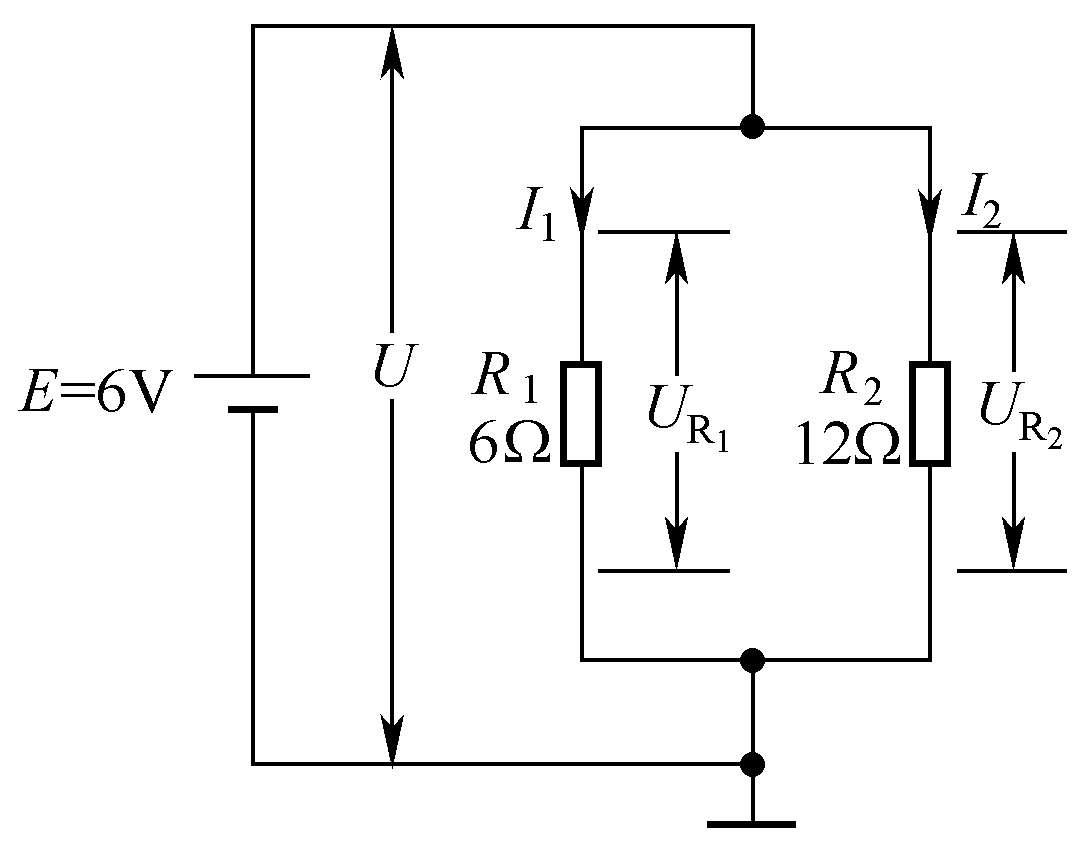
图1-6 电阻的并联
3.电阻的混联
一个电路中的电阻既有串联又有并联时,称为电阻的混联, 如图1-7所示。
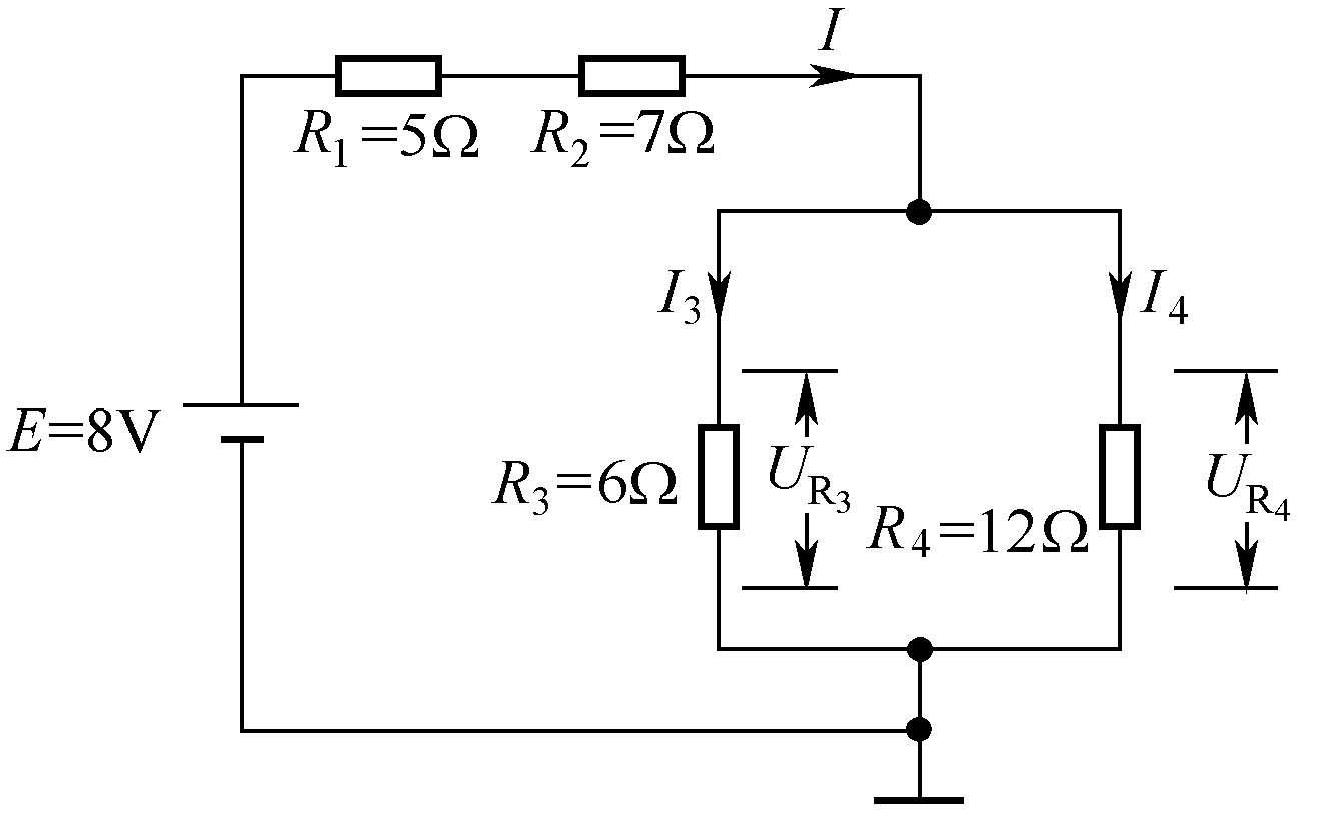
图1-7 电阻的混联
对于电阻混联电路,总电阻可以这样求:先求并联电阻的总电阻,然后再求串联电阻与并联电阻的总电阻之和。在图1-7中,并联电阻R3、R4的总电阻为
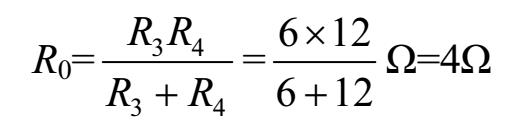
电路的总电阻为
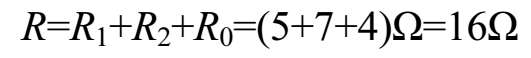
读者如果有兴趣,可求图1-7中总电流
I
,R
1
两端电压
U
R1
,R
2
两端电压
 ,R
3
两端电压
,R
3
两端电压
 和流过R
3
、R
4
的电流
I
3
、
I
4
的大小。
和流过R
3
、R
4
的电流
I
3
、
I
4
的大小。


