5.2 可导性

我们已经花了一些时间来学习连续性。现在该来看看函数能够具有的另一种光滑性——可导性。这实质上意味着函数有导数。因此,我们会花相当一部分时间来研究导数。发展微积分的最初灵感之一来自试图去理解运动物体的速度、距离和时间的关系。因此,让我们从那里开始,之后再回到函数。
5.2.1 平均速率
想象一下,在高速路上给一辆汽车拍照。曝光时间非常短,因此图像并不模糊——你甚至不能分辨那辆车是不是在动。现在,我问你:拍照时汽车的运动速度有多快?你说,没问题,只需使用经典公式
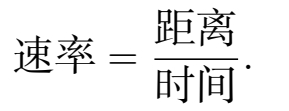
但问题是,照片无法告诉你距离(那辆车没有动)或时间(照片实质上是捕捉了一瞬间)。因此,你无法回答我的问题。
嗯,但如果我告诉你,拍照之后的一分钟,汽车行驶了一英里呢?这时你就可以使用以上公式来计算了,汽车一分钟开了一英里,速率是 60 英里/小时。但仍旧,你如何知道汽车在那一分钟里的速率是一样的呢?在那一分钟里,它可能会有多次的加速和减速。你不知道在那一分钟的开始时刻它究竟开得有多快。事实上,上述公式并不精确:等号左边应该称为 平均速率 ,因为那是我们所能知道的全部。
好吧,看你可怜,我再告诉你,在第一个 10 秒钟,汽车行驶了 0.25 英里。现在,你可以使用该公式来计算,在第一个 10 秒钟内的平均速率是 1.5 英里/分钟或 90英里/小时。这有点帮助,但在这 10 秒钟里汽车仍旧可能改变过速率,因此我们仍然不知道在这段时间的开始时刻它开得有多快。不过速率也不可能跟 90 英里/小时差太多,毕竟在这么短的时间里,汽车只可能加速或减速这么多。
如果知道在拍照后的一秒钟里汽车走了多远,那将会更好,但这仍旧还不够。甚至 0.0001 秒都可能足以让汽车改变速率,尽管变化不会太大。如果你感到我们是在取极限的话,那你想得没错。不过,我们首先需要看一看速度的概念。
5.2.2 位移和速度
想象一下,汽车在一条长直的高速路上行驶。公路上的里程标志牌有点奇怪:某个点上是 0 标志,在其左侧,标志始于−1 并且变得越来越负;在其右侧,一切一如平常。事实上,整个情形看上去就像图 5-8。

图5-8
假设汽车始于 2 英里处并直接驶向 5 英里处,那么它行驶的距离是 3 英里。但如果它是始于 2 英里处但向左行驶到了−1 英里处,它行驶的距离也是 3 英里。我们想要区分这两种情形,因此我们将使用 位移 来代替距离。位移公式就是:
位移=终点位置−初始位置。
如果汽车从位置 2 驶到位置 5,那么位移是 5 −2=3 英里。但如果是从位置 2 驶到了位置−1,那么位移是(−1)−2=−3 英里。因此,和距离不一样,位移可以是负的。事实上,如果位移是负的,那么汽车将终止于它初始位置的左侧。
距离和位移的另外一个重要区别就是,位移仅仅涉及终点和初始位置,汽车在行驶过程中的情况是无关紧要的。如果它从 2 走到 11,然后又返回到 5,距离是9 + 6=15 英里,但总位移仍然只是 3 英里。而如果它从 2 走到−4 然后又返回到2,位移实际上是 0 英里,尽管距离是 12 英里。然而,如果汽车只向一个方向行驶,没有后退的话,那么距离就是位移的绝对值。
正如我们在上一节看到的,平均速率是行使距离除以行驶时间。如果你用位移来代替距离,你会得到 平均速度 。也就是,

同样,速度可以是负的,而速率必定是非负的。如果在一定的时间段内,汽车有一个负的平均速度,那么它终止于初始位置的左侧。而如果在一定的时间段内平均速度是 0,那么汽车终止于它的初始位置。注意到,在这种情况下,汽车或许有一个很高的平均速率,尽管其平均速度为 0!一般而言,就像位移,如果汽车沿着一个方向行驶,那么平均速率就是平均速度的绝对值。
5.2.3 瞬时速度
现在,我们用速度来重新考察一下前面提到的重要问题:在给定的瞬间,如何测量汽车的速度?如前所述,基本思想就是,在始于拍照时刻并变得越来越小的时间段上,求汽车的平均速度。下面就是如何用符号来表达这个思路。
令 t 是我们关心的时刻。例如,如果全程始于下午两点,你可能决定要以秒表记,并用 0 表示开始时间。那种情况下,如果拍照时间是下午两点零三分,那么你将取 t =180。不管怎样,假设 u 是 t 之后很近的时刻。我们写 v t ↔ u 表示汽车在始于时间 t 终止于时间 u 的时间段上的平均速度。现在,让 u 越来越靠近 t 。多近呢?能有多近就多近!而这正是轮到极限登场的地方。事实上,
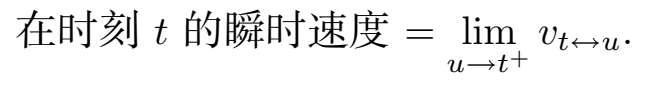
不过,为什么要忽略在时刻 t 之前的细节呢?通过允许 u 在 t 之前,我们可以让以上定义变得更一般一些。然后,我们可以用双侧极限替换右极限:
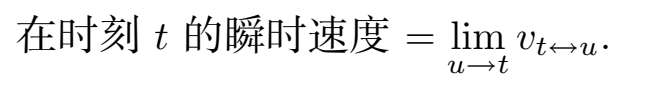
现在需要更多的公式。假设知道在高速路上汽车在任意时刻的准确位置。特别是,假设在时刻 t ,汽车的位置是 f ( t )。这就是说,令
f ( t )=汽车在时刻 t 的位置。
现在就可以准确地计算平均速度 v t ↔ u 了:
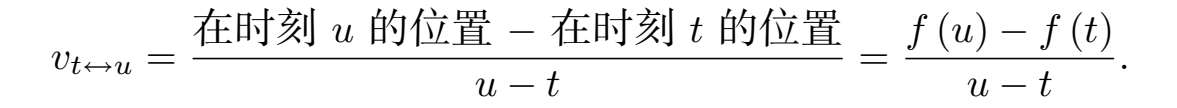
注意到分母 u − t 是所涉及时间段的长度(如果 u 在 t 之后的话 [1] )。不管怎么说,现在来取 u → t 时的极限:
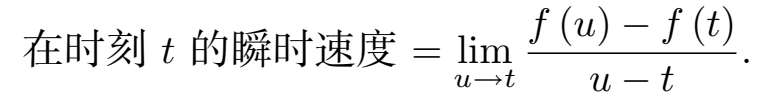
当然,在以上极限中,不能只是用 u = t 作替换,因为那样的话,会得到 0/0 的不定式。你现在还是要使用极限形式。
再来看一个稍有变化的变体。我们定义 h = u − t 。由于 u 非常靠近 t ,两时刻的差值 h 一定非常小。确实,当 u → t 时,可以看到 h →0。如果在上述极限中作如此替换的话,由于 u = t + h ,也会有

该公式和前一个公式没有实质性差别,只是写法不同而已。
让我们来看一个小的例子。假设处于静止状态的汽车从 7 英里标志处向右开始加速,并设此时刻 t =0 小时。结果表明,汽车在时刻 t 的位置好像是 15 t 2 + 7(这里的数 15 取决于加速度)。暂且不去担心为什么会如此,让我们设 f ( t )=15 t 2 + 7,并看看是否可以求出汽车在任意时刻 t 的速度。
使用上述公式有

现在展开( t + h ) 2 = t 2 + 2 th + h 2 ,并进一步化简,看到上述表达式变为
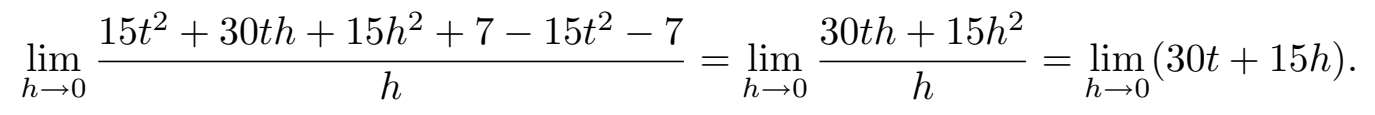
在最后一步,从分母中消去了 h ,这非常好,因为是它造成了所有的麻烦。现在,就可以将 h =0 代入并看到
在时刻
t
的瞬时速度=
 =30
t
。
=30
t
。
因此,在时刻 0,汽车的速度是 30 ×0=0 英里/小时——汽车处于静止状态。半小时之后,在时刻 t =1/2,它的速度是 30 ×1/2=15 英里/小时。一小时之后,速度是 30 英里/小时。事实上,在时刻 t 的速度是 30 t ,这个事实告诉我们,汽车行驶得越来越快,每小时速度增加 30 英里/小时。也就是说,汽车以 30 英里每二次方小时加速。
5.2.4 速度的图像阐释
是时候来看看图像了。再次假设 f ( t )代表汽车在时刻 t 的位置。如果想要在特定时刻 t 的瞬时速度,需要选取一个靠近 t 的时刻 u 。让我们来画一下 y = f ( t )的图像,并标注位置( t,f ( t ))和( u,f ( u ))以及过这两点的直线,如图 5-9 所示。
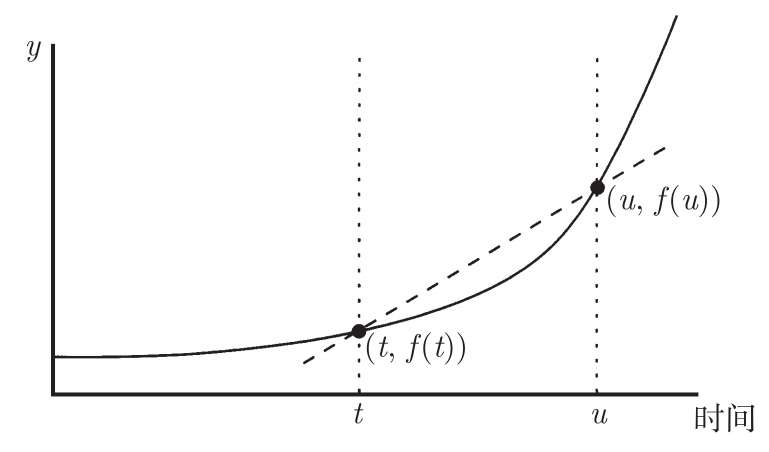
图5-9
该直线的斜率由公式
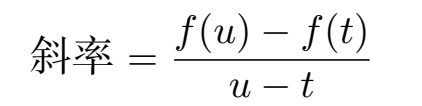
给出,这正好就是上一节中平均速度 v t ↔ u 的公式。因此就有了在 t 到 u 时间段上平均速度的图像阐释:在位置与时间的图像上,它就是连接点( t,f ( t ))和( u,f ( u ))的直线的斜率。
让我们来试着给瞬时速度找一个类似的阐释。我们需要取 u 趋于 t 时的极限,因此要重复几次上述图像,每一次 u 会越来越接近固定值 t ,如图 5-10所示。

图5-10
这些直线看上去好像越来越接近点( t,f ( t ))处的切线。由于瞬时速度是这些直线在 u → t 时的极限,于是,瞬时速度就等于通过点( t,f ( t ))的切线的斜率。看起来需要对切线有更好的了解……
5.2.5 切线
假设在某个函数 f 的定义域上选取一点 x ,那么点( x,f ( x ))位于 y = f ( x )的图像上。我们想要试着画一条通过该点并与该曲线相切的直线,即要找到一条切线。直观上,这意味着要找的直线刚好掠过该曲线的点( x,f ( x ))。切线不是只能与曲线仅相交一次!例如,图 5-11 中通过点( x,f ( x ))的切线与曲线还有第二次相交,这不成问题。
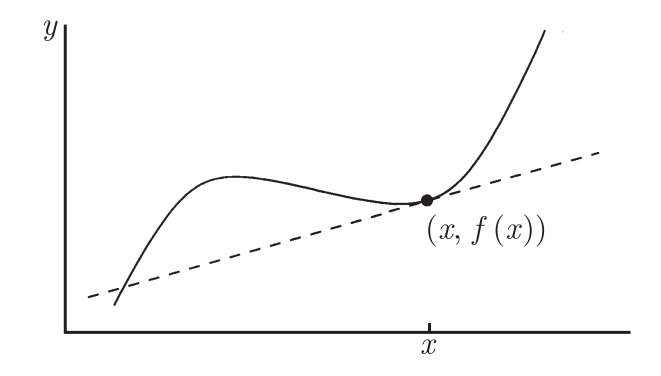
图5-11
也可能在一个图像上给定的一点没有切线。例如,考虑
y
=
 的图像,如图5-12 所示。该图像通过点(0,0),但过那一点没有切线。毕竟,怎么可能会有切线?不管怎么画,都不能在那里同时顾及两边的图像,因为它在原点处有一个尖点。在后面的 5.2.10 节将返回到该例子。
的图像,如图5-12 所示。该图像通过点(0,0),但过那一点没有切线。毕竟,怎么可能会有切线?不管怎么画,都不能在那里同时顾及两边的图像,因为它在原点处有一个尖点。在后面的 5.2.10 节将返回到该例子。
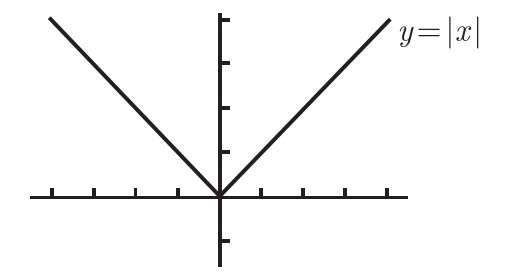
图5-12
即使通过( x,f ( x ))的切线存在,你又该如何找到它呢?回想一下,为了描述一条直线,仅仅需要提供两个信息:直线上的一点和该直线的斜率。然后,就可以使用点斜式来求直线方程。其实,我们已经有了一个要素了:直线通过点( x,f ( x ))。现在,只需要求出斜率。为了求解,我们将玩一个游戏,类似于在上一节中求瞬时速度玩的那个。
我们由选取一个靠近于 x (在它的左边或右边)的数 z 开始,并在曲线上画出点( z,f ( z ))。现在,画一条通过点( x,f ( x ))和( z,f ( z ))的直线,如图 5-13 所示。
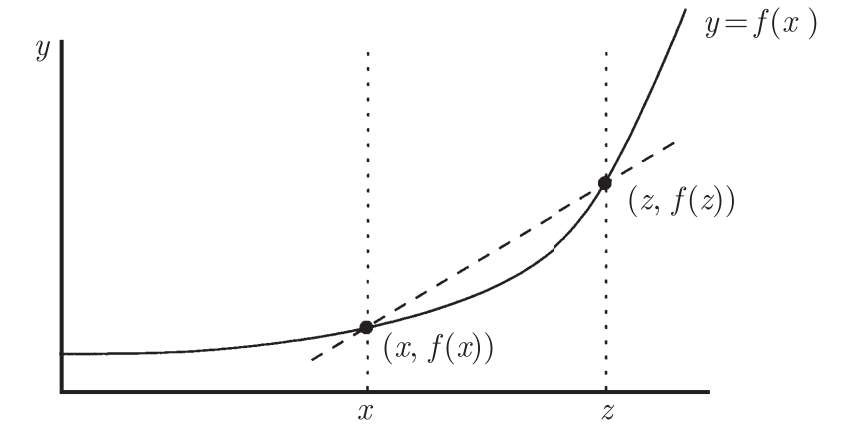
图5-13
由于斜率是对边比邻边,则虚线的斜率是
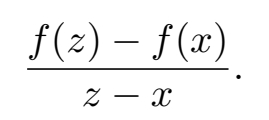
现在,当点 z 越来越接近 x ,但没有真正到达 x 的情况下,以上直线的斜率应该变得越来越接近要找的切线的斜率。因此,显然有
通过(
x,f
(
x
))的切线的斜率=

设 h = z − x ,可以看到,当 z → x 时,有 h →0,从而也有
通过(
x,f
(
x
))的切线的斜率=

当然,这只有当极限确实存在的时候才说得通!
5.2.6 导函数
在图 5-14 中,我在曲线上画了通过三个不同的点的切线。
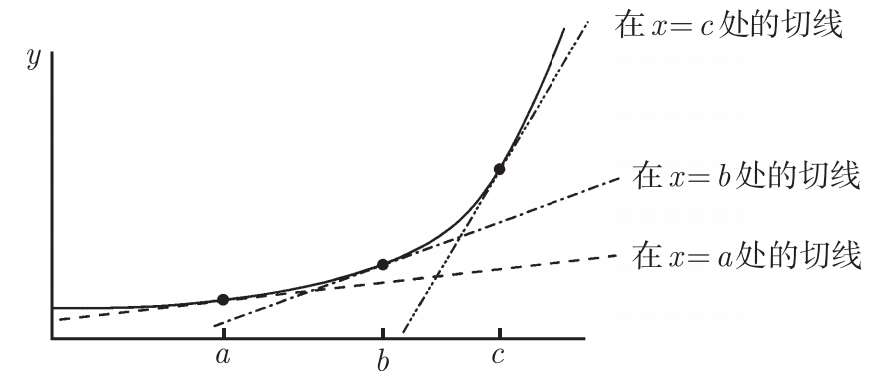
图5-14
这些直线有不同的斜率。也就是说,切线的斜率取决于你选取的点 x 的值。换句话说,通过( x,f ( x ))的切线的斜率是 x 的一个函数。这个函数被称为 f 的 导数 ,并写作 f' 。我们说,对 f 关于变量 x 求导 得到函数 f' 。根据上一节结尾部分的公式,如果极限存在的话,有
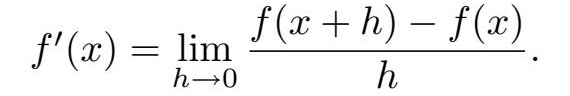
在这种情况下,
f
在
x
点
可导
。如果对于某个特定的
x
,极限不存在,那么
x
的值就没有在导函数
f'
的定义域里,即
f
在
x
点
不可导
。有很多原因会导致极限不存在。比如说,那里有一个尖角,就像前述
y
=
 的例子中那样。从更基本的层次上说,如果
x
没有在
f
的定义域中,那么甚至不可能画出点(
x,f
(
x
)),更不用说在那里画一条切线了。
的例子中那样。从更基本的层次上说,如果
x
没有在
f
的定义域中,那么甚至不可能画出点(
x,f
(
x
)),更不用说在那里画一条切线了。
回忆一下 5.2.3 节中瞬时速度的定义吧:
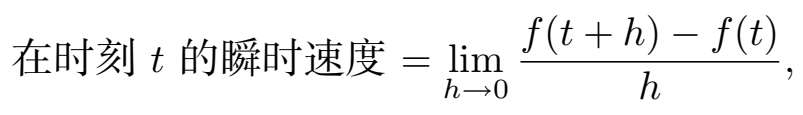
其中 f ( t )是汽车在时刻 t 的位置。等号右边的表达式和上述 f ' ( x )的定义一样,只是用 x 代替了 t !这就是说,如果 v ( t )是在时刻 t 的瞬时速度,那么 v ( t )= f ' ( t )。速度正是位置关于时间的导数。
来看一个关于求导的例子。如果 f ( x )= x 2 ,那么 f ' ( x )是什么呢?计算过程和 5.2.3 节结尾部分很相似:
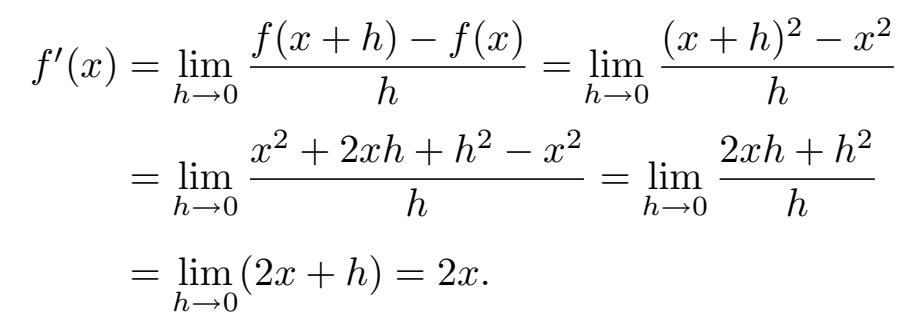
因此, f ( x )= x 2 的导数由 f ' ( x )=2 x 给出。这意味着,抛物线 y = x 2 在点( x,x 2 )的切线的斜率就是 2 x 。让我们画出该曲线和一些切线来检验一下,如图 5-15 所示。

图5-15
在 x =−1 处的切线的斜率看起来的确是−2,这与公式 f ' ( x )=2 x 是一致的。(两倍的−1 是−2!)其他切线也一样,它们的斜率都是相应的 x 坐标的两倍。
5.2.7 作为极限比的导数
在导函数 f ' ( x )的公式中,必须求出量 f ( x + h )的值。这个量是什么呢?其实,如果 y = f ( x ),将 x 变为 x + h ,那么 f ( x + h )只是一个新的 y 值。量 h 代表对 x 作了多少改变,因此用量△ x 作替换。这里的符号△表示“在……中的变化”,因此△ x 就是在 x 中的变化。(不要把△ x 看作是△和 x 的乘积,否则是错的!)因此,用△ x 替换 h ,来重新写一下 f ' ( x )的公式:
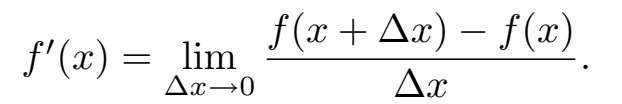
好了,情况是这样的。由( x,y )开始,其中 y = f ( x )。现在,选取一个新的 x 值,称之为 x 新。 y 的值也会相应地变成 y 新,这当然就是 f ( x 新 )。现在,任意量的改变量正好是新值减去旧值,因此有两个方程:
△ x = x 新 − x 和△ y = y 新 − y 。
第一个方程说的是 x 新 = x + △ x ,因此第二个方程现在可以变形为
△ y = y 新 − y = f ( x 新 )− f ( x )= f ( x + △ x ) − f ( x )。
这就是上面 f ' ( x )定义中分数的分子!这意味着
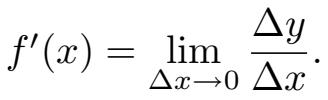
该公式的一个阐释是, x 中的一个小的变化产生了大约 f ' ( x )倍的 y 中的变化。的确,如果 y = f ( x )= x 2 ,那么在上一节已经看到 f ' ( x )=2 x 。让我们将精力集中在例如当 x =6 时的情况。首先注意到,由 f ' ( x )的公式可知 f ' (6)=2 ×6=12。因此,如果取等式 6 2 =36 并将 6 作一点点改变,36 将会变化 12 倍于此的量。例如,如果把 0.01 加到 6 上,就应该将 0.12 加到 36 上。因此,我会猜(6.01) 2 应该差不多是 36.12。事实上,确切答案是 36.1201,因此我的猜测确实接近。
那么,为什么我没有得到确切答案呢?原因是, f ' ( x )并不真正地等于△ y 和△ x 的比值,它等于当△ x 趋于 0 时该比值的极限。这意味着,如果没有离 6 太远的话,可能会做得更好。让我们来试着猜一下(6.0004) 2 的值吧。将原始的 x 值 6 加上了 0.0004,因此, y 值应该有 12 倍于此的改变,也就是 0.0048。因此,我们猜测(6.0004) 2 大约是 36.0048。这还不错——真正的答案是 36.004 800 16,两个数已经非常接近了!对 6 的改变越小,我们的方法计算出的结果就会越好。
当然,魔力数字 12 仅仅当从 x =6 开始的时候才会起作用。如果从 x =13 开始的话,魔力数字就是 f ' (13)了,它就等于 2 ×13=26。因此,我们知道 13 2 =139,那(13.0002) 2 是什么呢?为了从 13 得到 13.0002,必须加上 0.0002。由于魔力数字是 26,必须将 26 倍的 0.0002 加到 169 上来得到我们的猜测。这就是说,将 0.0052加到 169 上并得出猜测结果是 169.0052。再一次地,这相当不错:(13.0002) 2 实际上 169.005 200 04。
不管怎样,我们在第 13 章讲解线性化时将返回到这些基本思想上来。现在再来看看公式
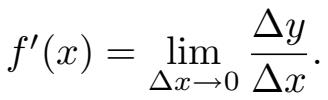
等号右边的表达式是,当
x
中的变化非常小时,
y
中的变化与
x
中的变化的比值的极限。假设
x
小得以至于其中的变化几乎注意不到。现在我们不写△
x
,它表示“
x
中的变化”,而是写d
x
,它表示“
x
中的十分微小的变化”。对
y
也有类似的表示方法。不幸的是,d
x
和d
y
本身没有什么意义
 ;尽管如此,这给了我们灵感,可以用一种不同的且更方便的方法来写导数:
;尽管如此,这给了我们灵感,可以用一种不同的且更方便的方法来写导数:
如果
y
=
f
(
x
),那么可以用
 来代替
f
'
(
x
)。
来代替
f
'
(
x
)。
例如,如果
y
=
x
2
,那么
 =2
x
。事实上,如果用
x
2
代替
y
,会得到对于一件事情的很多不同的表达方式:
=2
x
。事实上,如果用
x
2
代替
y
,会得到对于一件事情的很多不同的表达方式:
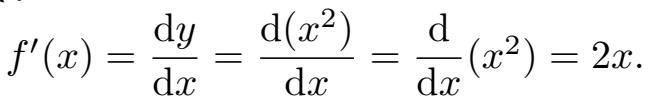
作为另一个例子,在 5.2.3 节,我们看到过,如果汽车在时刻
t
的位置是
f
(
t
)=15
t
2
+ 7,那么它的速度是 30
t
。回想一下,速度就是
f
'
(
t
),这意味着
f
'
(
t
)=30
t
。但如果我们决定把位置称为
p
,从而
p
=15
t
2
+ 7,便可以写
 =30
t
。这里的要点是,不是所有的量都用
x
和
y
来表达,你必须能够应对其他的字母。
=30
t
。这里的要点是,不是所有的量都用
x
和
y
来表达,你必须能够应对其他的字母。
总而言之,量
 是
y
关于
x
的导数。如果
y
=
f
(
x
),那么
是
y
关于
x
的导数。如果
y
=
f
(
x
),那么
 和
f
'
(
x
)是一回事。最后,请记住,量
和
f
'
(
x
)是一回事。最后,请记住,量
 实际上根本不是一个分数,它是当△
x
→0 时分数
实际上根本不是一个分数,它是当△
x
→0 时分数
 的极限。
的极限。
5.2.8 线性函数的导数
让我们暂停一下喘口气,回到一个简单的例子:假设 f 是线性的。这意味着,对于某个 m 和 b , f ( x )= mx + b 。你认为 f ' ( x )会是什么?回想一下,它度量的是,曲线 y = f ( x )在点( x,f ( x ))处的切线的斜率。在这个例子中, y = mx + b 的图像就是斜率为 m 、 y 轴截距为 b 的一条直线。显而易见,该条直线上任意一点的切线就是这条直线本身!这意味着,不管 x 取何值, f ' ( x )的值就应该是 m ,因为曲线 y = mx + b 有固定的斜率 m 。用公式检验一下:
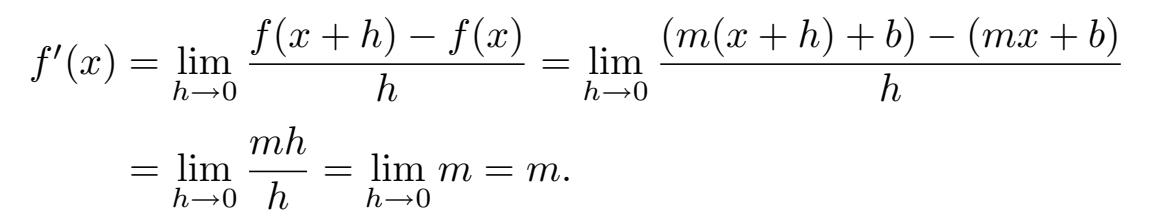
因此,不管 x 取何值, f ' ( x )= m 。这就是说,线性函数的导数是常数。如你所想,只有线性函数有固定的斜率(这是所谓的中值定理的结果,具体参见 11.3.1 节)。顺便说一下,如果 f 是常数函数,即 f ( x )= b ,那么其斜率总是 0。特别是,对于所有的 x , f ' ( x )=0。因此,这证明了常数函数的导数恒为 0。
5.2.9 二阶导数和更高阶导数
由于可以由一个函数 f 出发,取其导数得到一个新的函数 f' ,实际上可以采用这个新的函数,再次求导。最终得到导数的导数,这被称为 二阶导 ,写作 f'' 。
例如,如果 f ( x )= x 2 ,那么其导数为 f ' ( x )=2 x 。现在,我们想要对此结果求导。设 g ( x )=2 x ,并试着求出 g ' ( x )。由于 g 是一个线性函数,其斜率为 2,从上一节我们知道 g ' ( x )=2。因此, f 导数的导数是常数函数 2,这样就证明了,对于所有的 x , f '' ( x )=2。
如果
y
=
f
(
x
),那么我们已经看到,可以用
 代替
f
'
(
x
)。对于二阶导有一种相似的记号:
代替
f
'
(
x
)。对于二阶导有一种相似的记号:
如果
y
=
f
(
x
),那么可以用
 代替
f
''
(
x
)。
代替
f
''
(
x
)。
在上述例子中,如果 y = f ( x )= x 2 ,我们已经看到
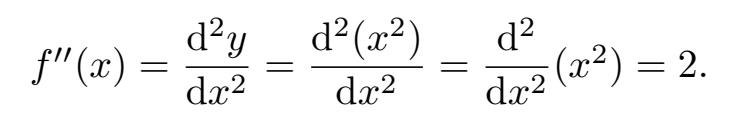
这些都是对 f ( x )= x 2 (关于 x )的二阶导是常数函数 2 的有效的表达方式。
为什么要止步于求二阶导呢?函数 f 的三阶导是 f 的导数的导数的导数。这可是一长串“导数”!,你应该把 f 的三阶导看成是 f 二阶导的导数,并且可以用以下任意一种方式写出:
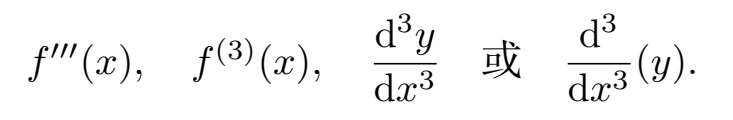
记号 f (3) ( x )对于高阶导数尤其方便,因为写那么多的撇号简直太傻了。因此,四阶导,即三阶导的导数,就可以写作 f (4) ( x )而不是 f'''' ( x )。尽管如此,对于低阶导数,有时候用这种方式表示也会很方便,比如将二阶导写成 f (2) ( x )而不是 f '' ( x )。甚至也可能将一阶导写成 f (1) ( x )而不是 f ' ( x ),因为只取了一次导数,此外,还可以用 f (0) ( x )代替 f ( x )本身(没有取导数!)。用这种方式,任何导数都可以写成 f ( n ) ( x )的形式,其中 n 为整数。
5.2.10 何时导数不存在
在 5.2.5 节,我提到过
f
(
x
)=
 的图像在原点处有一个尖点。而这应该意味着,在
x
=0 处导数不存在。现在来看看为什么会是这样。使用导数公式,有
的图像在原点处有一个尖点。而这应该意味着,在
x
=0 处导数不存在。现在来看看为什么会是这样。使用导数公式,有

我们感兴趣的是 x =0 时会发生什么,因此在以上等式链中用 0 替换 x ,得到
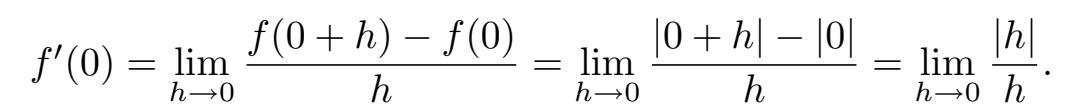
我们之前看到过这个极限!事实上,在 4.6 节,该极限不存在。这意味着, f ' (0)的值无定义,即 0 没有在 f' 的定义域中。然而我们也看到过,如果将它由一个双侧极限改为单侧极限,那么以上极限存在。特别是,右极限是 1,左极限是−1。这激发了 右 导数 和 左导数 的思想,其定义分别为

它们看起来和普通导数的定义很相似,只是双侧极限(即当 h →0)分别由右极限和左极限所代替。跟在极限的情况一样,如果左导数和右导数存在且相等,那么实际的导数存在且有相同的值。同时,如果导数存在,那么左右导数都存在且都等于导数值。
不管怎样,这里的要点是,如果 f ( x )=| x |,那么在 x =0 处其右导数为 1,左导数为−1。你相信吗?让我们再来看看图 5-16。当从原点出发沿着该曲线向右移动时,它的斜率确实是 1 (事实上,斜率始终为 1,即如果 x > 0, f ' ( x )=1)。类似地,从原点出发沿着该曲线向左移动时,它的斜率是−1 (事实上,如果 x < 0, f ' ( x )=−1)。由于左侧斜率不等于右侧斜率,所以在 x =0 处导数不存在。
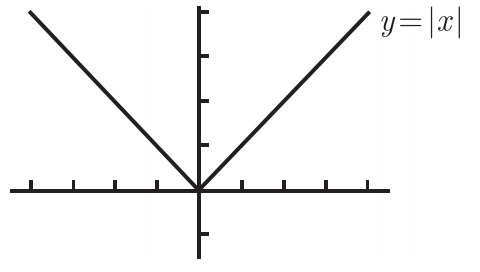
图5-16
现在,我们有了在其定义域内不是处处可导的连续函数。很明显,除了一个小点外,它仍然是可导的。事实上,你可以有这样一个连续函数,它是如此起伏多刺以至于它实际上在每一个单点 x 上都有一个尖角,因此它在任意点上都不可导!这种怪异的函数超出了本书的研究范围,但我要顺便提及,这种类型的函数可以用来为股价建模——如果你曾经看到过股价的图像,就会知道我说的起伏多刺是什么意思了。不管怎样,这里我的要点的是,存在不可导的连续函数。那么会有不连续的可导函数吗?回答是否定的,我们马上就会看到原因。
5.2.11 可导性和连续性
现在是时候将本章的两个重要概念联系在一起了。我将要表明,每一个可导函数也是连续的。换言之,如果你知道一个函数是可导的,那么你将买一赠一,获知该函数的连续性。更确切地说,我将要表明:
如果一个函数 f 在 x 上可导,那么它在 x 上连续。
例如,将在第 7 章证明,sin ( x )作为 x 的函数是可导的。这将自动暗示它在 x 处也是连续的。同样的结论也适用于其他的三角函数、指数函数和对数函数(除了在它们的垂直渐近线处)。
那么该如何证明我们这个重大断言呢?先来看看我们想证明的是什么。要证明 f 在 x 上连续,需要证明
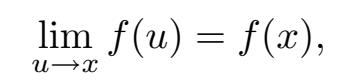
并且根据 5.1.1 节,只有当等号两边同时存在时,上式才成立!在继续证明之前,我想用 h = u − x 作替换,正如我们之前做过的。在这种情况下, u = x + h ,并且当 u → x 时,我们看到 h →0。因此,上式变为

我们需要证明等号两边都存在且相等——那样的话,就完成任务了。
目标已经明确,现在就让我们从实际知道的开始吧。我们知道 f 在 x 上可导;这意味着, f ' ( x )存在,因此根据 f' 的定义,极限
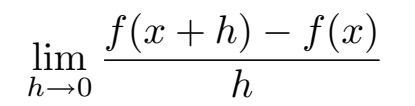
存在。首先注意到,上式中包含了 f ( x ),那么它一定存在,否则上式就无从谈起。因此,我们已经有所进展: f ( x )存在。但我们仍然需要想些聪明的办法。这里的技巧是,由另一个极限开始:
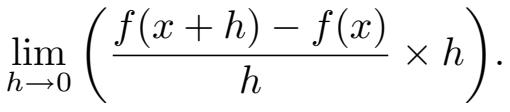
一方面,通过将它分成两个因子,可以求出该极限为
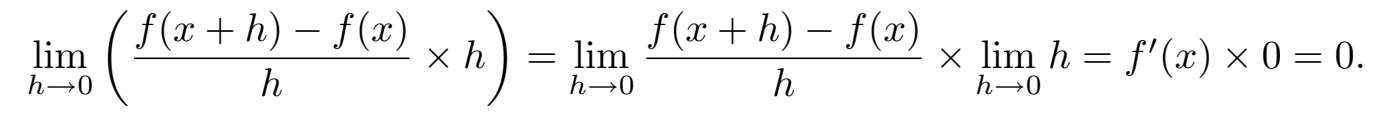
由于所有涉及的极限都存在,所以这样做没问题。(这里需要用到事实, f ' ( x )存在,不然就有问题了。)另一方面,可以取原始极限并消去因子 h 得到
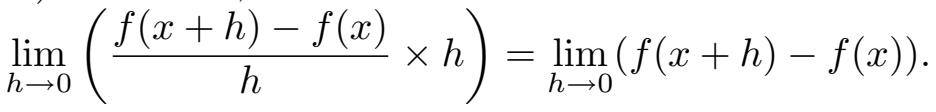
比较一下这两个式子,就会得到
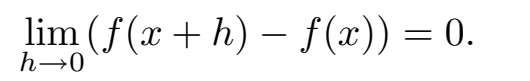
当然, f ( x )的值根本不依赖于极限,因此可以将它提出来,得到
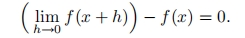
现在,只需将 f ( x )加到等号两边,得到
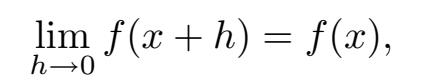
而这正是我们想要的!特别是,等号左边的极限存在并且等式成立。因此,我们证明了一个很好的结论: 可导函数必连续 。不过要记住,连续函数并不总是可导的!
[1] 如果 u 在 t 之前,那么分母应该是 t - u ,分子应该是 f ( t )− f ( u ),因此无论怎样都没问题!


