暴力、消散和合约收益
上一节,我构建了一个模型,它假设:既定数量的个体只有一个生产选项——开采黄金。同时,该模型还假定达成任何形式的协议或合约的成本都高到令人望而却步。在本节中,我们将放松这些假设,每次放松一个,然后推导出隐含的均衡条件。最重要的是,通过这一过程,我们可以得到一群人签订合约,分派个人产权的两个必要条件。
假设有N名同质的矿工,争夺C单位的均质土地。由于签约成本高到让人难以承受,矿工就转而采用暴力威胁。因为每个矿工都清楚知道其他矿工会为暴力分配多少劳动,所以没有资源被用于土地转让。当每名矿工都开采C/N单位土地的时候,均衡就达成了。现在假设在金矿地区以外存在一种经济体制,在这种体制下,签订合约是毫无代价的,所有的稀缺资源都有明确的产权分配。在这一体制下,土地产权的所有者得到的租金等于土地边际产品的价值。劳动(力)从这个体制转移到那些由于成本太高而无法达成合约的矿区,是不需要花费任何成本的。图2.7给出了原先N名矿工新的均衡条件。横轴代表每个矿工的个体劳动投入,纵轴代表劳动的边际产量。在C/N单位土地内开采的劳动边际产量为∂G/∂L。金矿区外的工资率为WW。每个矿工都会在C/N单位土地投入OL 1 单位劳动,并生产出OABL 1 单位黄金。任何剩余的劳动时间都会在矿场外为工资而工作。
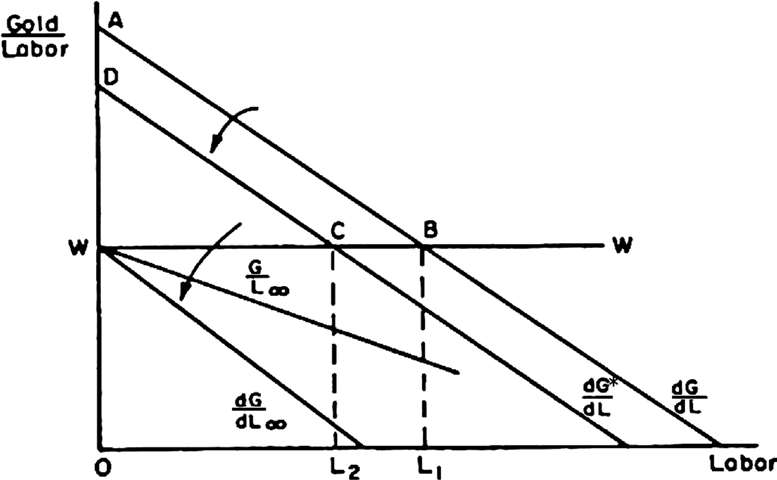
图2.7 拥挤导致的采矿收入消散
这N名矿工的收入都是WAB,高于其他非矿工的收入。因此,在假设没有进出成本的情况下,就会有更多的人转去采矿。假设一个靠工资为生的人被额外的收入所吸引,来到了矿场。他必须使用暴力威胁来获取土地。但是,如果他与原来的矿工完全相同,他可以为自己主张C/(N+1)单位的土地。这会减少N名矿工中每一个所拥有的土地数量,并将图2.7中的劳动边际产量曲线降低到∂G/∂L*。每名矿工的新均衡是在C/(N+1)单位土地上投入OL 2 单位劳动,并产生WDC的超额收益。
只要采矿的超额收入大于零,就会吸引更多打工者到金矿区去。每个同质化的新进入者都可以通过暴力威胁主张相等份额的矿区土地。个人土地持有量将会减少,从而导致∂G/∂L向左移,直到所有的超额收益消除为止。这将发生在无限多数量的矿工在无限小的土地上投入无限少的劳动时。在图2.7中,∂G/∂L移动到了∂G/∂L ∞ 。此时,劳动的平均产量G/L ∞ 等于工资率WW,并且所有源自采矿的剩余收入都已消散。 [9]
当然,收入的消散与财富最大化是相悖的。如果每个人都能以零成本与他人签订合约,那么原来的N名矿工就可以贿赂那些靠工资为生的人,让他们不去金矿。 [10] 因此,让我们在一定程度上放宽矿场中签约成本高昂的假设。现在假定,矿工可以零成本与其他矿工签订合约,将他们的劳动联合起来,使用暴力将非矿工排除在外。但我们仍然假设,矿工与非矿工签订合约的成本过高。如果达成合约,这种矿工合约将标志着产权的出现:协议明确承认个人对其土地的权利,并帮助他维持这些私有权不受任何人的侵犯。
我们现在可以阐述达成这类合约的第一个必要条件。 通过签约联合武力来维持私有权,从而获取好处的前提是,在使用暴力方面必然存在规模经济 。规模经济意味着,一个人在暴力中提供1单位劳动的效率要低于由两个人提供的1单位劳动(每人各提供1/2单位劳动)。
下面的例子可以证明,想要从签约中获得好处,使用暴力的规模经济必须存在。假设N名原始矿工签订合约,将他们的劳动以暴力形式结合起来,将外人排除在C单位土地中任何一处的开采行列之外。由于土地是平均分割的,所以团体的边际单位土地价值,等于任何单个矿工的边际单位土地价值。由于所有矿工的劳动边际产量都相等,该团体愿意分配给暴力以保护土地边际产量的总劳动,等于任何个人为保护其边际单位土地而使用的总劳动。任何试图获得其第一单位土地的外来者会发现,不管原先的矿工是否达成了合约,这些土地都受到相同数量单位的劳动保护。唯一的区别是,单位劳动不是由一个人提供,而是由整个团体提供。如果没有规模经济,外来者在暴力中使用的1单位劳动仍然等于该团体的1单位劳动,那么他们就可以继续通过暴力威胁为自己主张C/(N+1)单位的土地,最终将导致矿区土地收入的全部消散。换句话说,矿工们没能从合约中获得任何好处。
假如存在规模经济,该团体就可以使用不到1单位劳动的暴力,驱逐一个威胁使用1单位劳动获得额外土地的外来者。对外来者来说,该均衡条件就跟他威胁一位更能使用暴力的矿工的均衡条件一样。他最终将得到更少的土地。在这种情况下,外来者将得到少于C/(N+1)单位的土地。如果外来者获得的土地足以产生超过工资的收入,那么将会有更多的外来者进入。只要他们使用个人暴力威胁,他们得到的土地就会比团体成员少。当外来者的超额收入完全消散后,进入采矿业的行为就会停止。如图2.7所示,此时新来者的平均产出等于工资率WW。但是,最初的N名矿工比新来的矿工拥有更多的土地。他们将赚取边际内租金(intramarginal rent),这个租金在这些假设下是无法消散的。
只有当外来者对该团体使用个人暴力威胁时,边际内租金才会存在。如果外来者之间能够以零成本签订合约,同样可以实现规模经济。他们通过同意将劳动结合起来使用暴力,就可以消除甚至超越初始矿工的优势。例如,一群外来者可以通过合约将他们的力量联合起来,去威胁最初的N名矿工。假如这两个团体实现同样的规模经济,那么他们使用暴力的能力会相等。其结果将与两名相同的个人在矿区土地问题上发生冲突的结果相同。每个人都能得到相同的份额。每个团体都将获得C/2单位的土地,每个人都将获得C/2N单位的土地。随着每位矿工的土地减少,他们的超额收益也下降了。如果仍然是正数,则其他的外来者会继续进入,直到所有的超额收益都被消散为止。边际内的租金将不复存在,因此,初始矿工从签订合约中得不到任何好处。
这就让我们得出了通过签约联合武力来维护私有权,从而获得好处的第二个条件。 “最先”占有某一资源并为其权利签订合约的群体,一定存在某些方面的优势 。
产生这种优势可能有几个原因。最先占领某块矿地的人群可能会发现,捍卫他们已占领的土地比接管他人所占领的土地更为容易。尽管假定所有的人在使用暴力的能力上都是一样的,但最初占领土地的人现在有了一个优势。原始矿工提供的一单位暴力比外来者提供的一单位更加有效。即使有这一优势,原始矿工群体也没有理由签订合约,除非还存在规模经济。假如这些规模经济体不存在,外来者只会使用个人暴力威胁。有了这种最初的优势,初始的那些个体就可以拥有超过均等份额的土地。当外来者进入采矿业并将其超额收入降至零时,原始群体中的个人仍然保留了边际内的租金。简言之,签约不会带来任何额外的好处。只有拥有了规模经济,外来者才能作为一个整体来竞争这些边际内租金。为了保护这些超额收入,原始矿工必须签订合约来实现同样的规模经济。
为说明“最先”占领矿地的人群可能存在优势的第二个原因,我们放松签约成本为零的假设。如果实现规模经济的签约成本为正数,那么原始矿工团体和外部团体都将不得不分配稀缺的资源,以达成任何显性协议。原始矿工的签约成本可能比外来者的低。那些“最初”的人组织一个团体来维护私有权的成本要比新来的人要低。虽然签约成本可能高得令人望而却步,但对原始团体来说却不是这样。在这种情况下,新来的矿工必须单独进攻,最终得到的土地将少于原始矿工。假如外来者的签约成本较高,但并没有到达令人望而却步的程度,那么他们就可以作为一个团体发起攻击。然而,新来矿工的收益将比“最初”矿工的收益少,少的这部分数额等于两方签约成本的差额。只有在超额收益(扣除签约成本后的净收益)为正时,新来的矿工才会进入。等到这些净超额收益为零时,就不会有更多的外部团体进入;但原始矿工仍将享有边际内租金,其金额等于他们的签约成本之差。
这种“最初”优势反映在许多法律和习俗中。“产权纠纷十有其九判占有人胜”(possession is nine-tenths of the law)这句老话似乎适用于各种资源。许多政府将矿地的产权授予发现者。排队的权利约定俗成受到尊重,而后来的“插队”者则令人反感,受到谴责。在餐馆里最先占到桌子的人通常会对桌子旁的椅子有一些权利。在谈话中最先发言的人会被礼貌地授予空间私有权,其他人不能打断。女售货员问:“谁是第一个?”然后相应地分配他们的服务。 [11]


