资源分配与非零成本暴力
假设
在上一章中,我们假设每个个体都是财富最大化者,他们可以将自己的劳动时间与土地结合起来生产黄金。每个矿工在土地和劳动方面都有一个线性齐次生产函数。由于签约成本高到令人望而却步,因此个人暴力决定了谁会获得稀缺的矿区土地。个人使用暴力的相对能力与第二章所定义的相同,现在我们只是放弃了这个假设:每个人都不需要付出代价(成本),就能知道其他人愿意为冲突分配多少劳动。确定胜利者的唯一方法就是实际使用暴力。假定劳动和黄金是以零成本强制执行的私有财产。
个体解
图3.1描述了采矿中土地的边际产量∂G/∂h和劳动的边际产量∂G/∂L。从第二章可知,如果1个边际单位的土地成本是2个单位的劳动,那么个人将继续使用暴力来获取土地,直到(∂G/∂h)/(∂G/∂L)=2为止。这种情况发生在土地与劳动之比为OD时,这时BC=CD或BD/DC=2。在该模型中,个人必须在暴力中实际使用劳动。每一单位土地花费2个单位劳动。通过图3.2,可以更清晰地说明这一点。
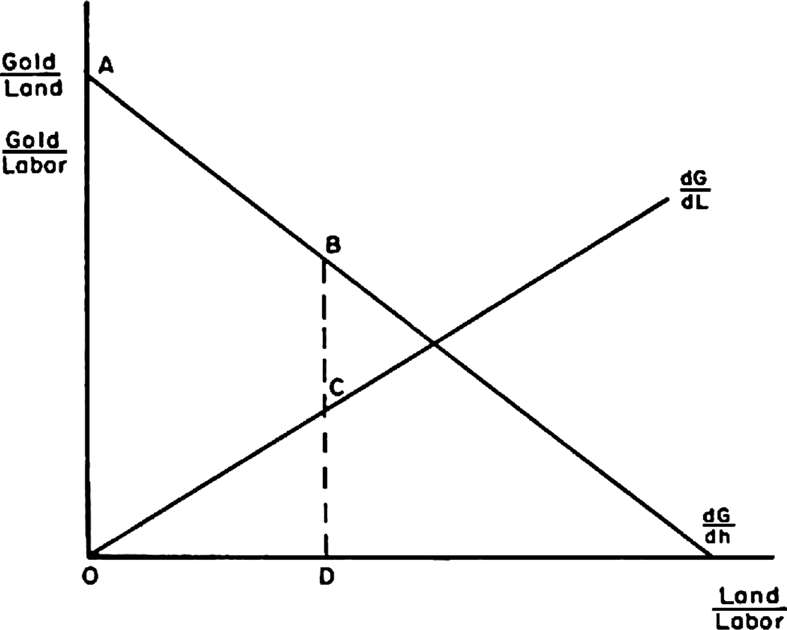
图3.1 正信息成本下的暴力使用与金矿土地分配:个体解
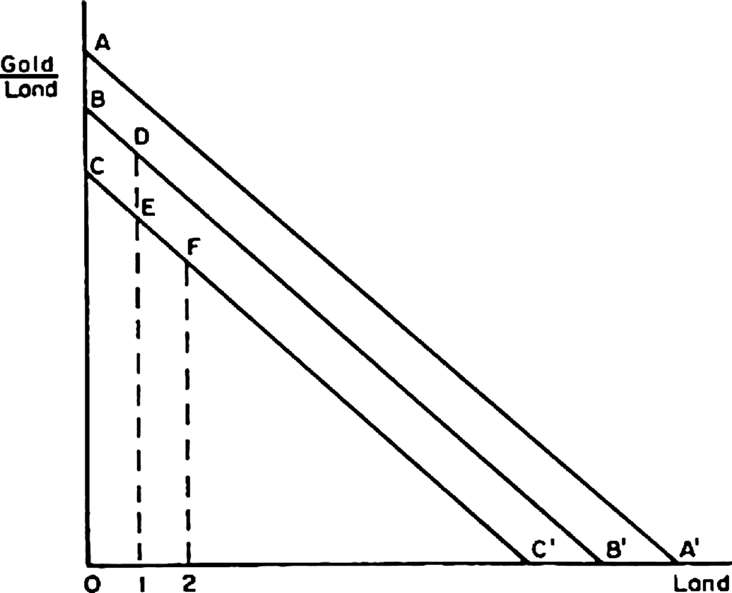
图3.2 暴力的成本:个体解
横轴代表个人在采矿中所使用的单位土地数量。纵轴代表在黄金方面的土地边际产量。直线AA′是这个人愿意在采矿中所使用的、联合了最大数量的
 单位劳动时,土地的边际产量∂G/∂h。为了将其他矿工驱逐于1单位土地之外,必须实际使用2单位劳动用于暴力。这时个人只剩下
单位劳动时,土地的边际产量∂G/∂h。为了将其他矿工驱逐于1单位土地之外,必须实际使用2单位劳动用于暴力。这时个人只剩下
 -2单位劳动可用于开采1单位土地。直线BB′表示与
-2单位劳动可用于开采1单位土地。直线BB′表示与
 -2单位劳动相结合时的土地边际产量。该矿工的黄金总产出为OBD1。为了获得另1单位土地,他将花费额外的2单位劳动,将∂G/∂h下移到了CC′。如果他使用暴力获得这第二个单位土地,他的黄金总产出将会增加到OCF2。这意味着净增加12FE-BDEC。如图3.3中所示,最终的均衡将出现在X单位的土地上。第X单位土地的黄金产出的净增长为PJKX-EDFJ=0。获得第X单位土地的边际成本,等于开采OP单位土地的边际劳动产出乘以用于获取额外土地的单位劳动数量。如果2个单位劳动被用于暴力,则放弃的黄金产量为EDFJ。有了额外的第X单位土地,剩余的劳动可以用来生产额外的PJKX黄金,相当于第X单位土地的边际产量。当PJKX=EDFJ时,额外土地的边际成本等于边际收益。
-2单位劳动相结合时的土地边际产量。该矿工的黄金总产出为OBD1。为了获得另1单位土地,他将花费额外的2单位劳动,将∂G/∂h下移到了CC′。如果他使用暴力获得这第二个单位土地,他的黄金总产出将会增加到OCF2。这意味着净增加12FE-BDEC。如图3.3中所示,最终的均衡将出现在X单位的土地上。第X单位土地的黄金产出的净增长为PJKX-EDFJ=0。获得第X单位土地的边际成本,等于开采OP单位土地的边际劳动产出乘以用于获取额外土地的单位劳动数量。如果2个单位劳动被用于暴力,则放弃的黄金产量为EDFJ。有了额外的第X单位土地,剩余的劳动可以用来生产额外的PJKX黄金,相当于第X单位土地的边际产量。当PJKX=EDFJ时,额外土地的边际成本等于边际收益。
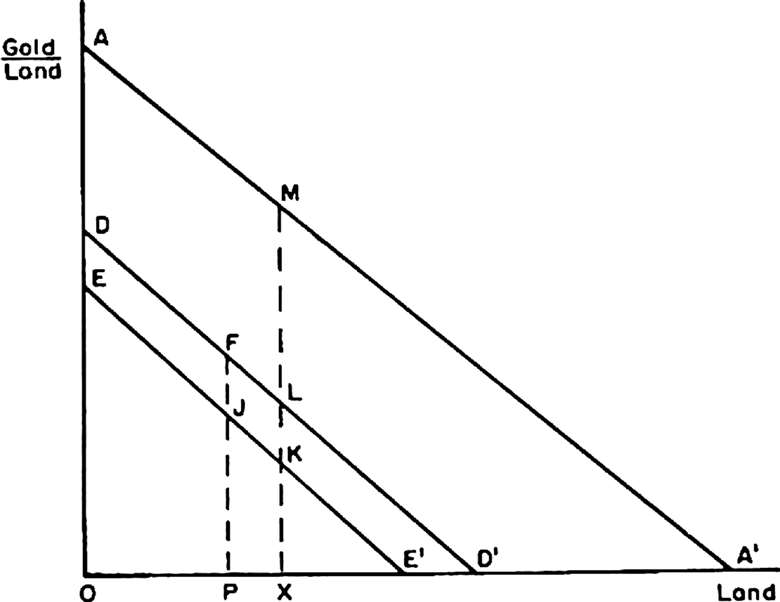
图3.3 采矿或暴力:个体均衡
该解与图3.1所示一致。当土地与劳动之比为OD时,土地的边际产量为DB,劳动的边际产量为DC。如果必须使用2个单位劳动来获取我们的单位土地,则边际成本为2CD,边际收益为DB(等于2CD)。图3.3提供了一些额外的信息。它显示了个人使用暴力将他人逐出矿地的总成本。在这个例子中,获得X单位土地的总成本是EAMK,也可以理解为,在没使用暴力时他本可以生产的产量与其将一些劳动付诸暴力后实际生产的产量之差。他的黄金总产量可达OEKX。
消散
在提出一般均衡解之前,我且先讨论一下暴力的成本。在图3.3中,面积EAMK代表获得OX单位土地私有权的个人总成本。EAMK表示的是因暴力而消散的矿区土地收入。请注意我们比较的两种极端情况。在一种情况下,我们假设不需要任何资源来签订私有权合约,而在另一种情况下,我们则假定签约成本高得令人望而却步。如果达成产权合约没有成本,则直线AA′将代表土地的边际产量。那么,面积OAMX将代表OX单位土地的最高黄金产量。如果达成合约的成本太高,而且实际上使用了暴力,那么EE′将代表土地的边际产量。面积OEKX将是OX单位土地的黄金总产量。OAMX和OEKX之差则是可能被个人消散掉的最大收入金额。 [1]
在没有签约成本的情况下,个体可以向其他个体支付不高于EAMK的数额,以避免使用暴力。如果签约成本不是零,每个个体都会尽量减少来自这种非私产性资源的收入消散。他可以通过多种方式做到这一点。例如,假设在他希望开采的每一段时间里,他都必须使用暴力不让他人进入,以维护他对土地的权利,那么,通过减少自己使用土地的时间,他就可以减少使用暴力的成本和由此造成的收入消散。通过加快开采黄金的速度——比独占(排他)无成本时的速度快,他将降低黄金的总产量。因此,某些收入将由于一种价值较低的土地使用方式而消散。如果节省的暴力成本大于因更快的采矿速度而减少的收入,那么他就会这么做。
同样,或许也可以通过使用一组不同的投入来降低暴力成本。有些采矿工具在采矿中使用成本较低,但很容易被偷。为了降低执行成本,可以使用一套不同的工具——一套更容易保护的工具。此外,虽然使用效率较低的采矿工具某些收入会消散,但因此节省的暴力成本可能更大。
除了以一种不同的方式使用非私产性资源之外,还可以通过合约减少消散。例如,他们可以签署合约,同意不使用暴力,并将土地权利分派给个人。不过即便这样,有一些收入还是会消散,因为合约的协商和执行都有成本。或者,假如每个矿工事先知道另一名矿工愿意为冲突分配多少暴力,则暴力行为就会减少。通过携带武器,其他矿工就知道他愿意在冲突中花费多少,从而减少了信息成本。有了这些信息之后,实际发生的暴力就会减少。不过,在这种情况下也存在消散,因为购买枪支、刀、子弹等都有成本。
尽量减少消散的努力,受到替代行动(要么以不同的方式使用资源,要么签约)的成本所约束。可以通过认定或观察,来确定不同行为的边际收益和成本。我们将因此得到隐含在黄金开采、采矿工具选择、武器选择和合约签署方面的资源分配情况。
在本章接下来的两部分中,我将试图解释合约的出现。为简化分析,假定在所有其他边际的替代上的成本是极为高昂的。也就是说,矿工没法改变每段时间的黄金开采率,也没法换成其他工具或其他采矿技术。在使用暴力赶走他人,占有某块土地后,如果不需要任何资源来保持独占,则他将继续用之前的劳动方式开采黄金。同样,在签约方面也不会有可替代的办法。个人暴力的唯一替代办法就是签订一项合约,给每个人都分配对某块土地的私有权。如果有人违反合约条款,所有矿工都将协助确保合约条款的执行。
一般均衡
对个人而言,我们假定他将其他矿工排除在边际土地之外的成本,是一个在模型之外确定的固定数额。为了说明这些成本是如何确定的,让我们假设有2名矿工,他们在开采和使用暴力方面的能力相同。他们正在争夺从数量有限的土地上开采黄金的权利。由于他们不知道暴力对抗的最终结果,因此必须使用资源来决定谁是胜利者。当其中一名矿工认定不再值得为边际土地战斗时,暴力行为就终止。图3.4说明了两名矿工的土地和劳动边际产量。
在每个矿工的土地与劳动之比为OQ的情况下,均衡条件就满足了。在土地与劳动之比为OQ时,矿工X和Y都愿意将QA/QB单位劳动用于暴力,把对方排除在边际单位土地之外。任何冲突都会导致平局。如果两名矿工都预计到获得额外单位土地的成本至少等于前一单位的成本,则不会发生后续的暴力事件。从图3.5上可以看出,这个假设是必需的。
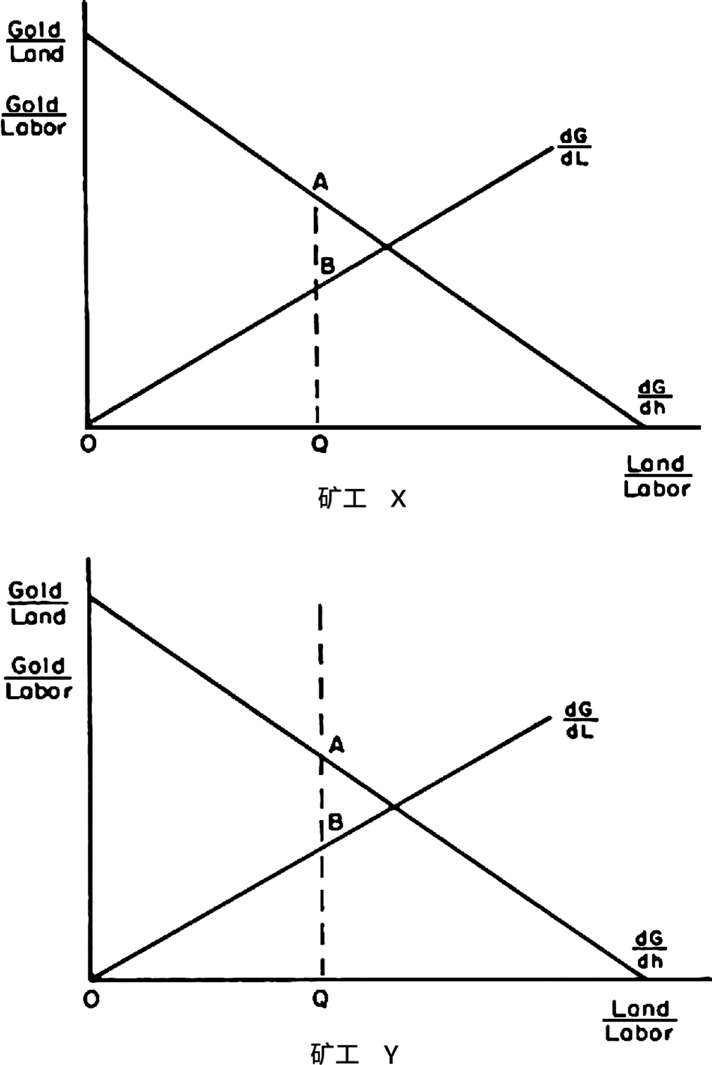
图3.4 暴力成本:一般均衡
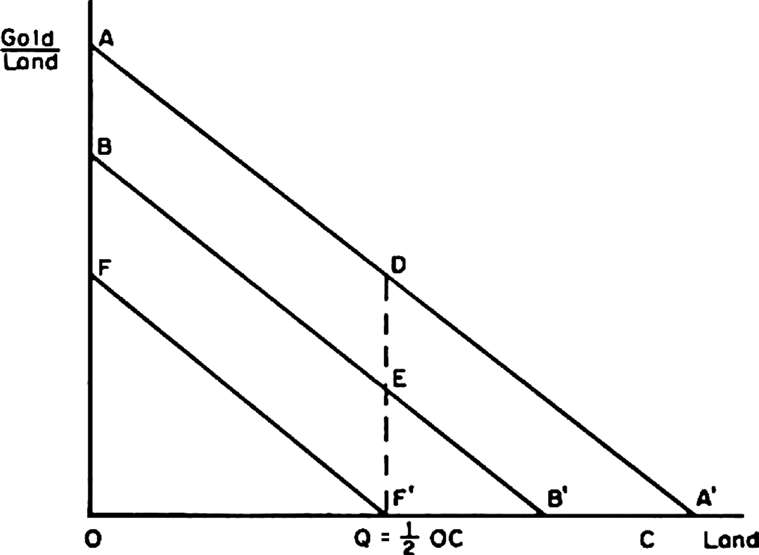
图3.5 收入的预期与消散
由于矿工X和Y都有相同的土地与劳动之比,并且分配了同样数量的劳动给暴力,因此每个人都必定拥有相同数量的土地。换句话说,他们会将土地的总量OC,分成相等的部分(½OC)。直线BB′是土地与采用暴力后所剩余的那些劳动联合时产生的边际产量(图3.4中的∂G/∂h)。在Q点上,边际土地价值对每个矿工来说等于QE,是一个正数。在争夺第Q单位土地的战斗中,每个矿工分配给暴力的劳动,其价值是因此放弃的黄金价值,它等于额外土地的价值。如果他们预期下一单位土地的价值低于第Q单位,那么暴力就会停止,每个矿工都会有Q单位土地。假如他们没有形成任何对额外暴力成本的预期(即没有对额外暴力成本有一个估计),他们就会继续战斗。土地的转让不会发生,但会有更多的劳动被用于暴力。这个情况将一直持续下去,直到∂G/∂h下移到FF′,额外土地的价值为零。每个矿工仍将拥有Q单位土地,但是暴力的总成本将是FADF′,而不是BADE。
需要注意的一点是,在这个二人模型中,暴力的实际使用不会改变第二章得出的土地均衡分布。每位矿工都能得到均等的份额。这可以一般化到N个完全相同的矿工通过暴力争夺矿地的经济上。在给定假设条件下,均衡必定发生在每个人都愿意分配相同数量劳动以获得额外单位土地的情况下。这将是他们各自拥有相同土地与劳动之比的时候。土地将平均分配给N名矿工。
非同质投入下的资源分配
暴力的实际使用不会改变第二章得出的土地均衡分布。能够更好地使用暴力的个人,仍将获得比其他人更多的土地。为了说明这一点,假设矿工X和Y在开采均质单位土地方面能力相同。如图3.5所示,通过暴力,土地被平分,每个矿工拥有Q单位土地。现在假设矿工X更擅长使用暴力。他在暴力上的一小时劳动相当于矿工Y两小时的劳动。在Q单位土地上,矿工X为获得额外一单位土地愿意花费的劳动,比矿工Y愿意用来保护这一单位土地所花费的劳动要多。矿工X将继续获得额外的土地,直到(∂G/∂h)/(∂G/∂L X )=1/2(∂G/∂h)/(∂G/∂L Y )为止。矿工X最终会比Y拥有更多土地。通过类似的推理,可以看出,劳动生产率较高的矿工最终得到的土地将比其他矿工要少。
当土地非同质时,均衡分布也与第二章所推导的相同。假设有N个完全相同的矿工,他们通过使用暴力将同质土地分割成相等的份额。其中有一个人——X发现,他拥有的那块土地比其他人的高产。由于拥有这块土地带来了更大的收入,其他矿工试图赶走X,以获取额外的黄金产量。为简化分析,我们假设,倘若其他矿工决定获取矿工X的部分土地,就必须放弃他们目前拥有的全部土地。那么只有当他们能够获得足够的土地,产生的收入(扣除暴力成本后)等于他们目前在低产土地上的收入的情况下,他们才会去攻击X。图3.6说明了这种情况。
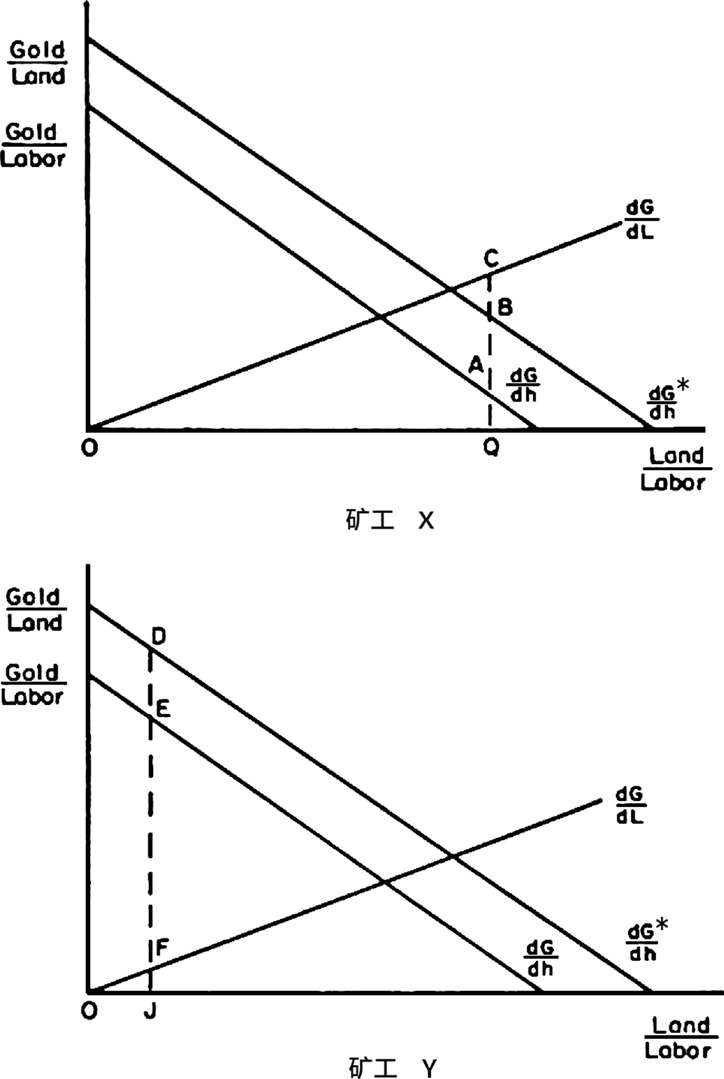
图3.6 暴力成本,非同质土地与财产分配
现在,矿工X拥有全部矿地的1/N,跟劳动结合后,他的土地与劳动之比就是OQ。矿工Y放弃了之前对其劣质土地的所有权主张,对矿工X使用暴力。在被发现产出更高之前,预期的土地边际产量是∂G/∂h,而∂G/∂h*是肥沃土地的实际边际产量。如果Y为保护自身土地而攻击任何其他矿工,他只愿意使用JE/FJ劳动来获得第一个单位土地。由于矿工X的土地价值更高,所以Y愿意用DJ/FJ劳动来获得第一个单位土地。另一方面,在矿工X的土地生产率提高之前,他只愿意使用QA/AC劳动来保护单位边际土地。现在,他愿意使用QB/QC劳动。如果他们使用暴力的能力相等,矿工Y将通过使用QB/QC暴力劳动将X逐出边际土地。当然,对于这两名矿工来说,当他们平分了矿工X原有土地份额时,这两人的最终均衡达成。在这个点上,两人的土地与劳动之比相等,都愿意分配同样数量的劳动来保护边际土地。
有两点值得强调。首先, 较肥沃的土地将以更小的数量被相同的个人占有 。当矿工Y放弃原有土地时,他就给其他矿工留下了更多低产的土地,减少了用于分配这片低产土地的暴力,并提高了这片土地上的个人黄金产量。由于矿工X和Y分割那块较肥沃的土地,因此每人只能分到较小块的土地。如果这些小块土地的黄金回报仍然超过较贫瘠土地的回报,则其他矿工将会使用暴力来获取一些肥沃土地。这种再分配会持续下去,直到每一块土地的净收益在任何地方都一样。其次,随着黄金土地价值的增加,将有更多的资源被用于暴力以驱逐他人。 随着土地价值的上升,任何个人将他人排除在外的成本,无论是总成本还是边际成本,都将上升。然而,生产力的提高只会通过暴力的增加而部分消散 。剩余的产量增加量将由N名矿工平均分配。
现在,区分获取土地的成本和长期保持私有权的成本就非常重要了。由于之前对这一点的分析只考虑了一个时间段(时期),因此这种区别并不重要。然而,在将个人暴力与作为确立和维持矿地私有权手段的合约做比较时,这一区别就显得十分重要。此刻,我们暂且假设矿工永远不会知道:假如其他一切保持不变,那么在每一时期使用的暴力都不会改变土地的初始分配。每段时期他们都是重新开始,重新用暴力决定谁得到什么土地。虽然这一假设稍后会改变,但它有助于说明土地价值与通过暴力获取和维持私有权的成本之间的关系。
图3.7总结了前面章节的一些含意。横轴代表没有暴力成本时土地的黄金产量现值;纵轴代表任何个人获得和维持私有性的总成本现值。由于时间的引入,所有的价值都是现值。 [2] 45度直线是每一段时期内所有土地收入都通过暴力消散的点的轨迹。因此,暴力成本的现值等于采矿收入的现值。直线OV代表个人用于排斥其他矿工的资源现值。直线OV的位置是从前面的分析中得到的。它的位置表明,把其他人从没有黄金产量的土地上驱逐出去并不需要什么成本。随着潜在黄金产量的增加,暴力驱逐他人的成本上升,因此消散的收入也随之增加。然而,如前所述,在一个有N名矿工的封闭经济体中,并非所有的超额价值都消散了。这意味着,随着个人潜在黄金产量的增加,他将获得额外的收入。例如,如果潜在黄金产量的现值为OC,则暴力成本为CB,每名矿工的净收入为AB。
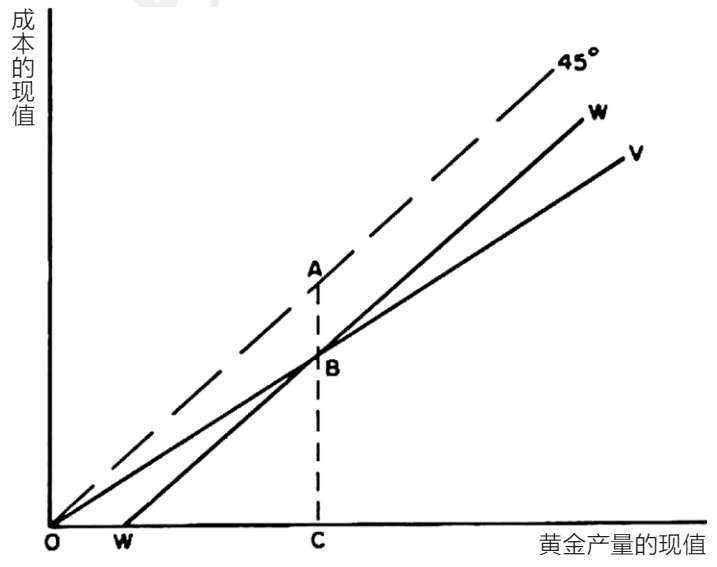
图3.7 暴力成本,消散与私有采矿权价值
假如现在向潜在进入者开放矿地,则情况会略有不同。假设任何想要采矿的外人都必须放弃他另谋高就所获得的全部收入,且只要采矿收入扣除暴力成本后仍超过另谋高就的收入,那么他就会进入。由于原始矿工还可以选择离开,在一个以零成本强制执行产权的经济体中赚取工资,因此OV将移向WW;只有当黄金产量的现值升至OW(相当于另谋高就的收入)时,任何人才必须使用暴力来阻止其他人开采土地。假如采矿业的净收入超过OW,新的竞争就会进入——从而增加了维护私有矿地的成本,直到超额价值全被增加的矿工和暴力消散为止。这是假定没有达成任何合约的情况。


