通过暴力分配资源的理论
假设
每个人都是财富最大化者,他能够把劳动时间和土地组合起来生产黄金。在劳动和土地方面,他的淘金生产函数是一次齐次的。在该模型中,对数量有限的金矿的权利,必须在既定数量的矿工之间进行分配。然而,由于所有的签约成本都高得让人难以承受,因此,只有通过暴力才能获得开采一小块土地的私有权。 [5]
暴力的概念,或者说对他人使用武力的概念,是模糊不清的。它可能包括实际使用枪支、刀具或拳头,也可能仅仅指威胁要使用以上手段。它也可能包括建造一座营寨或其他保护性建筑。为了澄清即将采用的概念以及简化分析,暴力将被定义为分配给对抗其他矿工时所使用的体力劳动时间。无论是真正用在枪战、格斗或修建保护墙的劳动时间,还是仅仅威胁采用这些手段的劳动时间,都包括在内。 [6] 一个矿工使用暴力将另一个人排除在某块土地之外的效果,并不取决于他的绝对能力,而是取决于他相对于其他矿工的能力。例如,假如两名矿工在使用暴力上的能力旗鼓相当,那么他们之间的任何冲突,都将通过每人分配到战斗中的劳动时间得以解决。假如他们在暴力上都分配了两个单位的劳动时间,结果将会是平局。如果其中一人使用了更多的劳动时间,那么他就会成为赢家。同样,假如一个矿工在暴力使用的效率上比别人高一倍,那么他只要用别人一半的劳动时间就能和其他人打成平手。
为了进一步简化分析,假设每个矿工都能够无成本地确定其他人愿意并且能够为特定冲突分配多少劳动时间。这个假设使我们能够解决冲突,而无须在暴力中真实使用稀缺资源(劳动)。因为假如事先已经知道结果,就没有人会去争斗。举个例子,假设两个矿工都想要得到某块土地的私有权。如果他们在使用暴利的能力上旗鼓相当,那么土地的产权最后归谁,就取决于谁愿意并且有能力分配最多的劳动时间用于争斗。争斗并不会真的发生。由于知道自己会输,失利者就会放弃他对那块土地的所有权主张。由于每一个矿工都清楚知道其他人愿意拿出来用于暴力的劳动时间长短,因此,这种假设可以让我们忽略任何博弈策略问题。
最后,为了将注意力只集中在一种非私有性的资源上,我将假设劳动(作为一种投入)和黄金(作为最终产品)都是以零成本执行的私有财产。
个体解
只要每个矿工愿意并且能够比其他矿工分配更多的劳动时间在暴力上,他都能把其他人排除在外,从而获得额外单位的土地。我们可以借助图2.1,来论证一下个人可以获得的土地均衡数量。
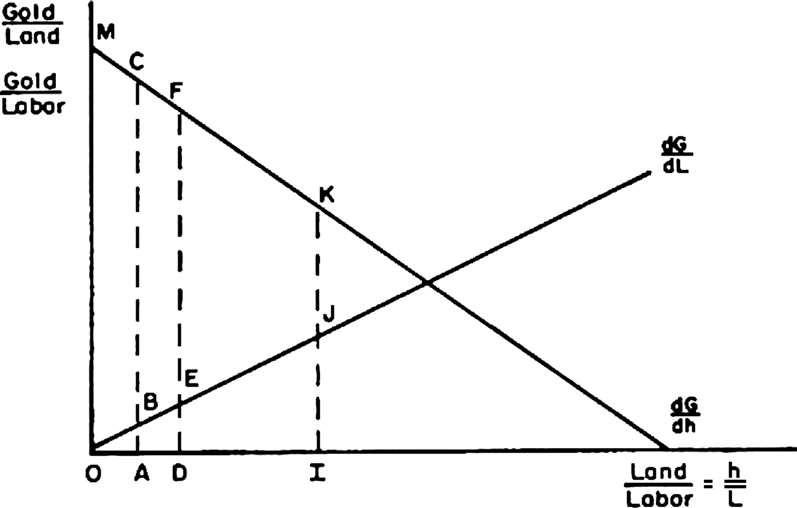
图 2.1 暴力使用与金矿土地分配:个体解
Gold/Land:黄金/土地;Gold/Labor:黄金/劳动;Land/Labor:土地/劳动;h:土地面积
在这幅图中,横轴代表土地与劳动之比,作为采矿过程中的投入。纵轴代表土地的边际产量(∂G/∂h)和劳动的边际产量(∂G/∂L)。不考虑工作与闲暇时间之间的权衡,这个人在该时期内愿意分配给采矿的劳动数量是固定的(
 )。
)。
土地的边际回报从原点开始就出现了递减。同时,根据线性齐次生产函数下的可变比例规律(law of variable proportions),劳动的边际产量开始上升。根据这个图,我们可以确定矿工愿意使用多少暴力来获取额外的矿地。比如,假设该矿工拥有OA单位土地。按照OA/
 情况下的土地与劳动之比(land/labor ratio),土地的边际产量为AC,劳动的边际产量为AB。他愿意为暴力分配AC/AB单位劳动,以获取额外1单位的土地。AC/AB只不过是该矿工在黄金生产上的边际替代率。它衡量的是,在不改变黄金总产量的情况下,为交换额外1单位某种投入,该矿工在另一种投入上能够放弃的最大数量。
情况下的土地与劳动之比(land/labor ratio),土地的边际产量为AC,劳动的边际产量为AB。他愿意为暴力分配AC/AB单位劳动,以获取额外1单位的土地。AC/AB只不过是该矿工在黄金生产上的边际替代率。它衡量的是,在不改变黄金总产量的情况下,为交换额外1单位某种投入,该矿工在另一种投入上能够放弃的最大数量。
用数值举例更加清楚。假设∂G/∂h=AC=10单位黄金;∂G/∂L=AB=1单位黄金。额外1单位土地将会增加该矿工10单位黄金的财富,但是额外1单位劳动只会增加他1单位黄金的财富。如果能够获得额外1单位的土地,他愿意最多将10单位的劳动付诸暴力。假如其他矿工使用暴力的能力相等,且愿意分配2个单位的劳动,让这个矿工远离他们的边际土地,那么他们将在冲突中沦为输家。在这个例子中,该矿工能在没有任何真实暴力发生的情况下获取额外的土地,因此他仍将拥有
 单位劳动用来采矿,以及额外1单位的土地。
单位劳动用来采矿,以及额外1单位的土地。
请注意,当这个矿工获得额外的土地时,他的土地与劳动之比增加了,但他把劳动分配给暴力的意愿却减少了。这是因为随着土地与劳动之比越来越高,∂G/∂h在持续下降,∂G/∂L在不断上升。换句话说,连续单位的土地变得越来越不值钱,而劳动则变得越来越有价值。在拥有OD土地的情况下,个人将会分配FD/ED劳动(这比AC/AB低)用于暴力,以获得另一单位土地。如果我们假设获取额外1单位土地的劳动成本是固定的2单位劳动,那么这个矿工将会继续通过威胁夺取他们的土地,直到他对额外单位土地的估值是他对额外单位劳动估值的两倍——这种情况会发生在他拥有OI土地的时候。当土地劳动比IK/IJ=2时,均衡实现。此时,这个矿工不会要求更多的土地——他不会愿意为获得额外1单位土地而再分配2单位劳动用于暴力,其他矿工亦是如此。由于每个人都事先知道任何冲突可能造成的后果,因此不会有更多的威胁发生,也不会有更多的矿地进行交换。这个矿工就能够通过OI单位土地和L单位劳动生产出OMKI单位的黄金。
在检验这个一般均衡解之前,需要对该模型作两点说明。首先,在这个模型中,土地的初始获取与持续维持私有性没有区别。这个区别在后面会很重要,但就目前而言,在该生产函数下,威胁使用暴力将他人排除在外是一种非常彻底的威胁,足以保证土地在整个时间段内的私有性。其次,我假定矿工只能将劳动用于采矿或暴力,除此之外,不存在其他的选择方案。如果是一个更为一般化的理论,比如说,可能会提供给他一个选择来分配一定的劳动时间,以提高其使用暴力的能力。事实上,我在这里假设的是,将劳动时间分配给其他边际(margins)的替代成本是极其高昂的。这点稍后会有更详细的讨论。
一般均衡
到目前为止,将其他矿工排除在一单位土地之外的成本都被认定为一个参数,其值并未在模型中确定。 [7] 在本节,我们将检验这些成本的决定因素。首先,假设有两名矿工在开采黄金方面具有相同的生产函数,而且在使用暴力方面具有同等的能力。他们在争夺一块有限的同质土地的开采权。图2.2说明了这种情况。
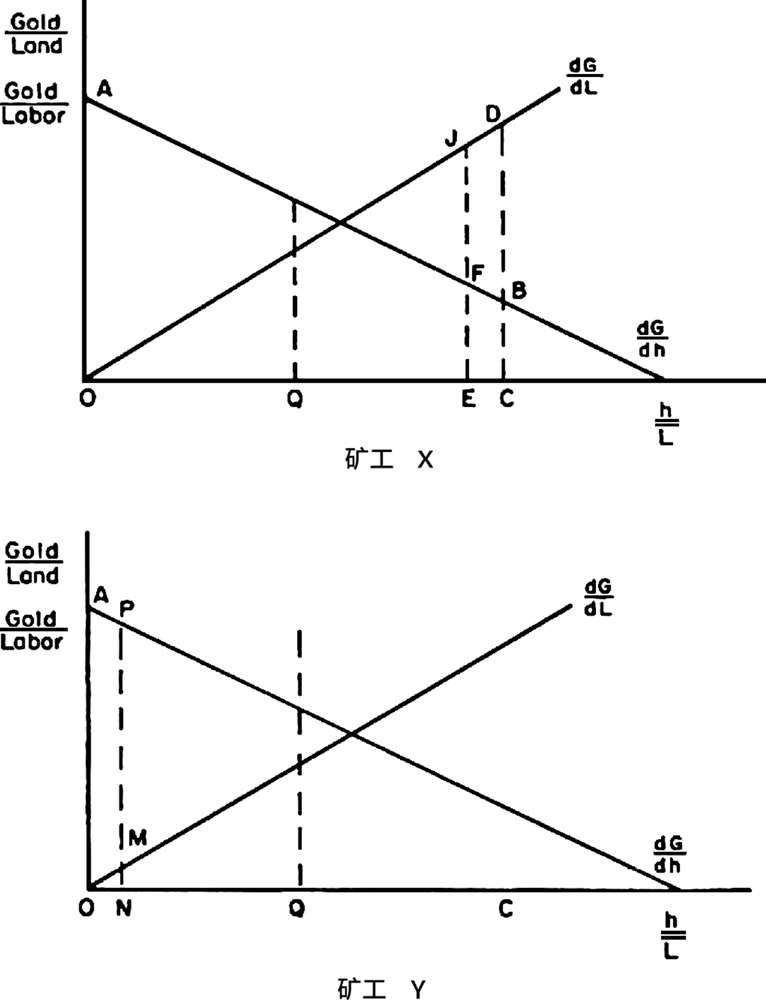
图2.2 两名矿工间的暴力使用与金矿土地分配
假如矿工Y没有出现,则矿工X就可以使用所有可用的土地(OC)和
 单位劳动以生产OABC单位黄金。他可能只愿意分配BC/CD单位的劳动,使Y远离最后1单位土地。另一方面,没有土地的矿工Y愿意使用AO/O单位的劳动,以获得第1个单位土地。由于他们使用暴力的能力旗鼓相当,矿工Y将在任何争夺第1单位土地的冲突中获胜。矿工X损失了1单位土地给矿工Y。实际上,转让过程中并没有使用任何资源——仅仅是使用了暴力威胁。在这次转让之后,矿工X留有OE单位土地和L单位劳动。现在X愿意分配EF/EJ单位劳动来保护他的边际单位土地,而Y则愿意使用NP/MN单位劳动将X逐出该单位土地。此时,Y将再次成为赢家。在该假设条件下,只要矿工Y愿意分配比矿工X更多的劳动用于暴力,则Y从连续单位土地中驱逐X的这一过程就会继续下去。而只要Y的土地与劳动之比小于X,他将继续从X那里获得额外的土地。只有当他们的土地与劳动之比相同时,转让才会停止。在这一点上,均衡实现。因为他们在额外单位的土地上都配置了相同的价值,所以任何更进一步的冲突都将会导致平局。在这一均衡点上,每个矿工都拥有相同数量的土地,即OQ=(1/2)OC。
单位劳动以生产OABC单位黄金。他可能只愿意分配BC/CD单位的劳动,使Y远离最后1单位土地。另一方面,没有土地的矿工Y愿意使用AO/O单位的劳动,以获得第1个单位土地。由于他们使用暴力的能力旗鼓相当,矿工Y将在任何争夺第1单位土地的冲突中获胜。矿工X损失了1单位土地给矿工Y。实际上,转让过程中并没有使用任何资源——仅仅是使用了暴力威胁。在这次转让之后,矿工X留有OE单位土地和L单位劳动。现在X愿意分配EF/EJ单位劳动来保护他的边际单位土地,而Y则愿意使用NP/MN单位劳动将X逐出该单位土地。此时,Y将再次成为赢家。在该假设条件下,只要矿工Y愿意分配比矿工X更多的劳动用于暴力,则Y从连续单位土地中驱逐X的这一过程就会继续下去。而只要Y的土地与劳动之比小于X,他将继续从X那里获得额外的土地。只有当他们的土地与劳动之比相同时,转让才会停止。在这一点上,均衡实现。因为他们在额外单位的土地上都配置了相同的价值,所以任何更进一步的冲突都将会导致平局。在这一均衡点上,每个矿工都拥有相同数量的土地,即OQ=(1/2)OC。
这种方法可以推广到N人经济体中。假设矿工X和Y处于均衡状态,双方都拥有OQ单位土地。此时,第三个矿工Z进入。如图2.3所述,假设矿工Z与矿工X和Y在采矿和暴力方面的能力相同。矿工X和Y各自愿意分配AQ/BQ
 单位劳动,将其他矿工从1边际单位土地上驱逐出去。矿工Z没有土地,他愿意使用DO/O单位劳动将X或Y拒于1边际单位土地之外。矿工Z将获胜,从X或Y处获得1单位土地。与其他人相比,只要Z愿意将更多的劳动用于暴力,他将持续把矿工X和Y从他们各自的土地上驱逐出去。为了尽量减少暴力的潜在代价,他将从最不愿意使用暴力的人那里获得额外的土地。只有当矿工X、Y和Z都拥有相同的土地与劳动之比时,才能达到均衡。在这里,他们每个人都愿意将PT/PS单位劳动分配给暴力,因此任何额外的冲突都会导致平局。有了OP单位土地和
单位劳动,将其他矿工从1边际单位土地上驱逐出去。矿工Z没有土地,他愿意使用DO/O单位劳动将X或Y拒于1边际单位土地之外。矿工Z将获胜,从X或Y处获得1单位土地。与其他人相比,只要Z愿意将更多的劳动用于暴力,他将持续把矿工X和Y从他们各自的土地上驱逐出去。为了尽量减少暴力的潜在代价,他将从最不愿意使用暴力的人那里获得额外的土地。只有当矿工X、Y和Z都拥有相同的土地与劳动之比时,才能达到均衡。在这里,他们每个人都愿意将PT/PS单位劳动分配给暴力,因此任何额外的冲突都会导致平局。有了OP单位土地和
 单位劳动,每个矿工都将生产ODTP单位黄金。
在这些假设下,矿地总量最终将会在相互竞争的矿工之间平均分配
。在本例中,矿工X、Y和Z各得到1/3的土地。如果有N名矿工,那么每人将获得总土地的1/n。
单位劳动,每个矿工都将生产ODTP单位黄金。
在这些假设下,矿地总量最终将会在相互竞争的矿工之间平均分配
。在本例中,矿工X、Y和Z各得到1/3的土地。如果有N名矿工,那么每人将获得总土地的1/n。
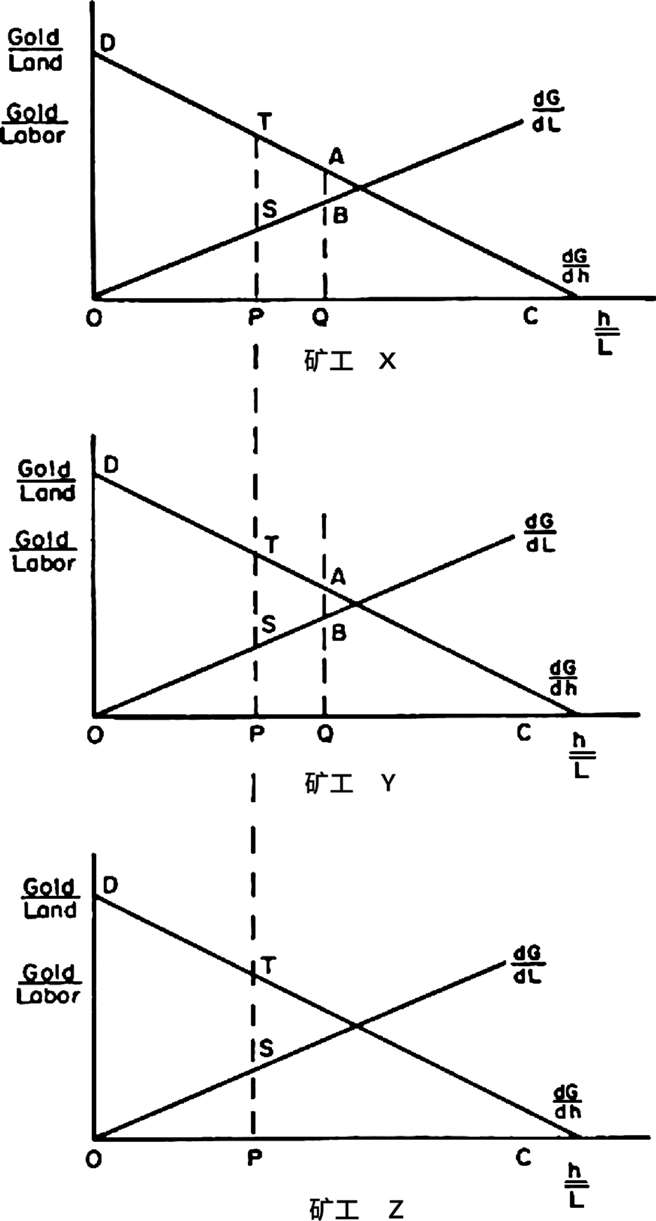
图2.3 三名矿工间的暴力使用与金矿土地分配
非同质投入情况下的资源分配
前几节我们假定,在采矿和暴力方面,劳动是同质的,并且就黄金产量而言,土地也是同质的。在本节中,我们将假定这些投入之间有差异,来研究隐含的资源分配。
首先,我将推出当一个矿工比另一个更善于使用暴力时的均衡条件。假设某块土地只有矿工X和Y在采矿。他们完全相同,土地的产能也一样。这些条件在图2.4中进行了说明。两名矿工都拥有OQ=(1/2)OC单位土地,并正在生产OABQ单位黄金。假设矿工Z在采矿方面的能力跟矿工X和Y一样,但他在使用暴力方面的能力却是矿工X或Y的两倍。根据定义,这意味着Z在使用暴力时的1单位劳动等于其他任一矿工2单位的劳动。土地以暴力威胁的方式转让,直到每个矿工都拥有OP=1/3OC单位的土地为止。这是每个矿工都有相同的能力使用暴力时的均衡状态,见图2.2。但现在,矿工Z使用1单位劳动用于暴力的效率是X或Y的两倍,在土地与劳动之比为OP/
 的情况下,每个矿工都愿意分配PS/PR单位劳动用于暴力,以获取额外的土地。矿工Z最多愿意把相当于矿工X或Y一半的劳动投入到暴力上,到时,他就会停止获得土地。在画出这些边际产量曲线后,最终的分配是,Z获得OT单位土地,X和Y获得OM单位土地。在OT单位土地和
的情况下,每个矿工都愿意分配PS/PR单位劳动用于暴力,以获取额外的土地。矿工Z最多愿意把相当于矿工X或Y一半的劳动投入到暴力上,到时,他就会停止获得土地。在画出这些边际产量曲线后,最终的分配是,Z获得OT单位土地,X和Y获得OM单位土地。在OT单位土地和
 单位劳动这一点上,矿工Z愿意花费1单位劳动(UT/UT=1)将矿工X或Y从额外1单位土地上驱逐出去。而在OM单位土地和
单位劳动这一点上,矿工Z愿意花费1单位劳动(UT/UT=1)将矿工X或Y从额外1单位土地上驱逐出去。而在OM单位土地和
 单位劳动这一点上,矿工X和Y都愿意花费2单位劳动(DM/NM=2),将其他人拒于1边际单位土地之外。因此,任何冲突都将导致平局,进一步的土地转让也不会发生。总的来说,我们可以得出结论,
在所有其他条件一样的情况下,在使用暴力上能力较强的人最终会比能力较弱的人得到更多的土地
。但他们不会获得所有的土地。矿工X和Y的黄金产量均为OADM,低于矿工Z的黄金产量OAUT。这个产量上的差异是矿工Z由于拥有较强暴力能力而带来的租金,是不会因竞争而消散的。
单位劳动这一点上,矿工X和Y都愿意花费2单位劳动(DM/NM=2),将其他人拒于1边际单位土地之外。因此,任何冲突都将导致平局,进一步的土地转让也不会发生。总的来说,我们可以得出结论,
在所有其他条件一样的情况下,在使用暴力上能力较强的人最终会比能力较弱的人得到更多的土地
。但他们不会获得所有的土地。矿工X和Y的黄金产量均为OADM,低于矿工Z的黄金产量OAUT。这个产量上的差异是矿工Z由于拥有较强暴力能力而带来的租金,是不会因竞争而消散的。
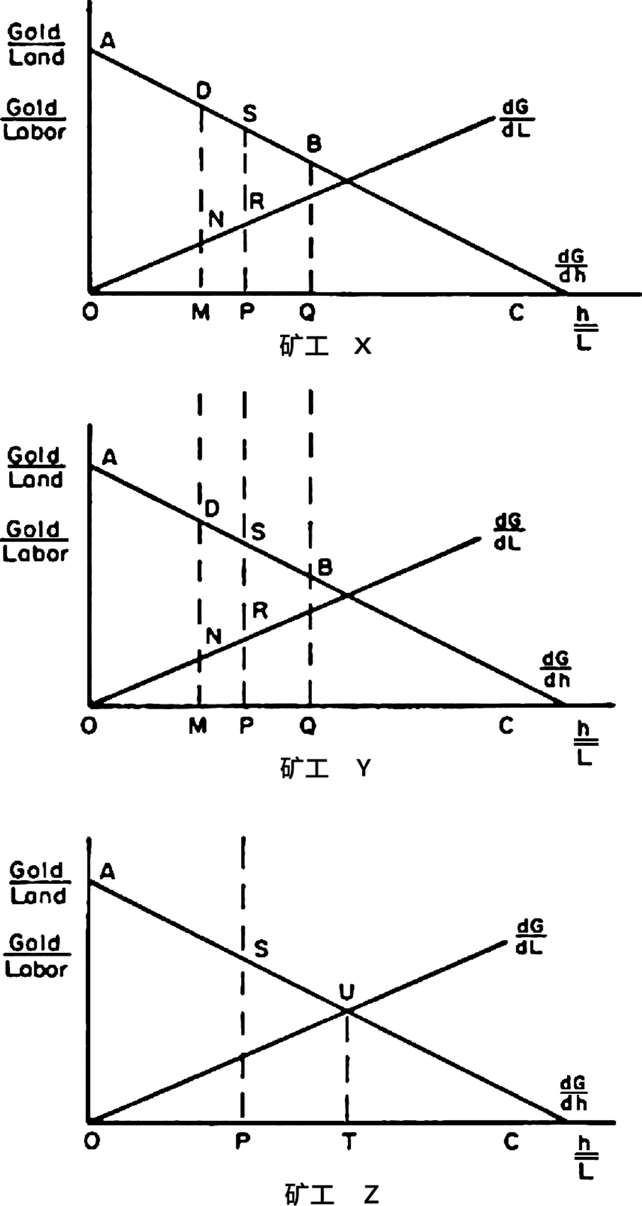
图2.4 由个体暴力能力差异导致的土地分配
这个解似乎显得“无效率”。三名矿工在黄金生产方面的能力都是完全相同的,而且土地也是同质的。通过重新分配土地,让每个矿工得到相等的份额,总产出就能得到增加。这种重新分配土地的方式,将保证边际生产率处处相等。届时,社会产出将达到最大值。矿工Z有更多的土地这一事实,意味着他的土地边际产量比矿工X或Y的边际产量要低。尽管这一切都符合事实,却是毫不相关的, 因为在该模型的局限条件下 ,不可能重新分配土地以获得更大的总产出。任何从矿工Z那里夺走并分配给矿工X或Y的土地,都会立即被Z重新主张。由于所有相关的边际等式都得到满足,这种均衡所隐含的总产出是一个社会最大值,因此解是有效率的。当然,如果局限条件改变,矿工将面对一组不同的选项,这一产出可能就不再是最大了。它不再是均衡,因为最大化者总是在假设的局限条件下追求最大化。这种讨论表明,逻辑上是不可能从基于局限最大化的模型中推导出“无效率”的。 [8]
为了说明当一个矿工在采矿上比其他矿工更优秀时均衡条件的变化,假设矿工X、Y和Z各有OP=1/3OC单位的土地(如图2.5所示)。同时假定土地同质,且每个矿工使用暴力的能力相等。现在,假定矿工Z在采矿方面更有效率——这由∂G/∂L到∂G*/∂L的平移来表示。均衡状态不再是OP。由于矿工Z在采矿中的劳动生产率提高了,他将劳动分配给暴力的成本也就增加了。在拥有OP单位土地时,矿工Z愿意分配BP/BP=1单位劳动用于使用暴力,以保护他的边际土地。而矿工X和Y则会愿意花费PB/DP>1单位劳动来获得更多的土地。矿工Z会把土地让给矿工X和Y,直至(∂G/∂h)/(∂G*/∂L Z )=(∂G/∂h)/(∂G/∂L X )=(∂G/∂h)/(∂G/∂L Y )。这发生在矿工Z的OQ处和矿工X、Y的OR处。根据这些土地与劳动之比,他们每个人都愿意将同样数量的劳动分配给暴力,而进一步的冲突将会导致平局。土地不再进行转让。请注意, 生产率更高的矿工最终得到的土地实际上会少于其他矿工 。
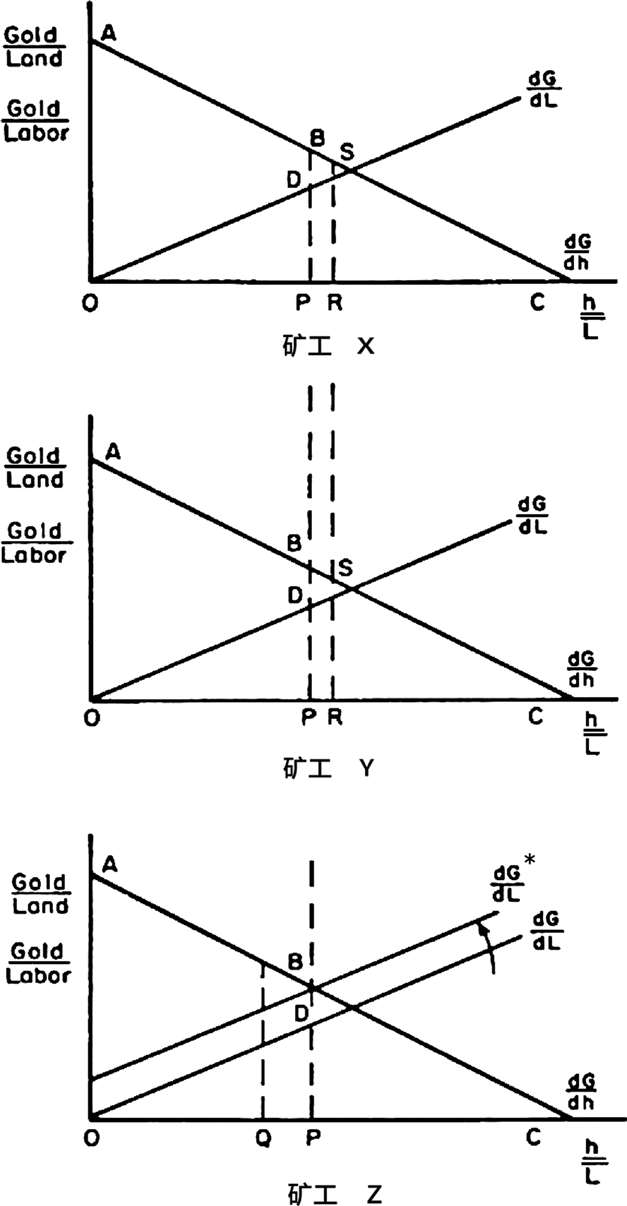
图2.5 由个体采矿能力差异导致的土地分配
矿工X和Y在使用OR单位土地和
 单位劳动的情况下,都能够生产OASR单位黄金,这大于拥有OP单位土地时的黄金产量。由于边际产量曲线的相对位置发生了位移,矿工Z的黄金产量变得更加难以确定。我们知道,如果矿工Z的生产率只是跟矿工X或Y一样高,那么每个人都会拥有OP单位土地,并生产OABP单位黄金。然而,当矿工Z的劳动生产率较高时,必须保证黄金总产出更大,才会让他选择放弃一些土地,要不然他宁愿分配更多的劳动来维持原有的OP单位土地。
单位劳动的情况下,都能够生产OASR单位黄金,这大于拥有OP单位土地时的黄金产量。由于边际产量曲线的相对位置发生了位移,矿工Z的黄金产量变得更加难以确定。我们知道,如果矿工Z的生产率只是跟矿工X或Y一样高,那么每个人都会拥有OP单位土地,并生产OABP单位黄金。然而,当矿工Z的劳动生产率较高时,必须保证黄金总产出更大,才会让他选择放弃一些土地,要不然他宁愿分配更多的劳动来维持原有的OP单位土地。
在每单位土地生产率不相等的情况下,也可以确定均衡条件。假设矿工X、Y和Z在采矿和使用暴力上能力相等。如果单位土地是同质的,则每个矿工的均衡将会处于图2.6中的OP值。个人的黄金产出将为OAQP。假设矿工Z发现,他的土地OP Z 比其他土地都要高产。从图形上在OP的那一段,将会出现∂G/∂h到∂G*/∂h的平移。虽然矿工Z的土地生产力提高了,但他将劳动用于暴力来获得额外土地的意愿并没有发生变化,因此,他仍旧处于均衡状态。然而,如今矿工Z的黄金产量为OBDP,比矿工X或Y都高。所以其他矿工愿意放弃自己的土地,来换取矿工Z开采的土地。为简化分析,假设从一块土地转移到另一块土地的决策是一个全部或零(all-or-nothing)的决策。矿工X或Y不可能在保留原始土地的同时,还能从矿工Z那里取得边际单位的土地。如果他们想要得到Z的土地,就必须放弃自己以前的所有财产,还不得不使用暴力威胁来获得一些更加高产的土地。
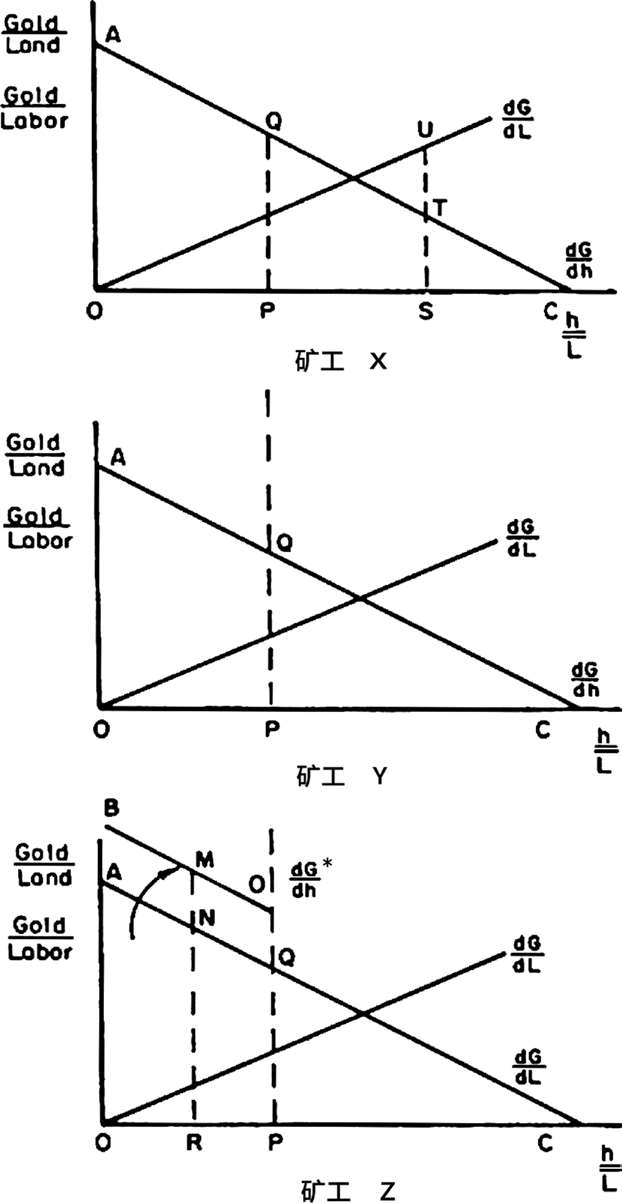
图2.6 由土地生产率差异导致的土地分配
这一假设并不是为了此处论证的需要才临时提出的。如果不同生产率的土地相隔一定距离,那么劳动从一块土地转移到另一块土地的成本可能会很高,以至于妨碍开采每一块土地中的某些土地。假设矿工Y决定离开他的土地,以便用暴力威胁矿工Z。这将造成两种影响。第一,矿工Y腾出来的土地会留给矿工X,于是矿工X的土地持有量增加到2OP=OS,并使其黄金产量提高到OATS。第二,由于矿工Y和Z具有相同的采矿能力和战斗力,他们将各自获得相同份额的原属于Z的土地,即1/2(OP)=OR。Y和Z将各自生产OBMR单位黄金,我将假定这等于矿工X的总产量。根据这种土地分配方式,没有人有任何激励去做出改变。矿工Y和Z都想要更多的较高产土地;但由于他们都愿意使用相同数量的劳动驱逐对方,所以任何冲突都会导致平局。此外,矿工Y和Z都不会为获得矿工X的部分土地而离开自己较为高产的土地,因为这将导致他们黄金总产量的下降。这是一个均衡状态。 拥有较高产土地的个人所得到的土地数量,会比那些拥有较低产土地的个人少 。
请注意,此均衡并不满足最初模型中的边际条件。由于矿工X愿意将TS/SU单位劳动分配给暴力,而矿工Y和Z愿意各自将RM/RN单位劳动分配给暴力,因此边际替代率TS/SU与RM/RN不相等。由于全部或零的假设,这个均衡是不同的。相关的决策边际不再是1额外单位的土地,而是额外的黄金产量。为了攻击矿工Y或Z,矿工X必须牺牲他的全部黄金产量。矿工X这么做的前提是:他在这片更加肥沃的土地上的预期份额将会比他目前拥有的土地产出更多的黄金。只要生产率更高的土地给矿工X个人带来的黄金产量超过其他地区的,矿工X就会离开自己的土地来威胁Y和Z。
到这里为止,我一直都认为:在没有任何协议的情况下,解决冲突的唯一途径是威胁或使用个人暴力。在我的假设前提下,通过暴力分配资源是可以推测的。在其他条件相同的情况下,更有能力使用武力的人将会比其他人得到更多的土地。那些劳动生产率较高的矿工将得到较少的土地,而那些在较高产土地上开采的人拥有的土地比在较低产土地上的矿工少。


