2.5 其他误差机理
2.5.1 刀具磨损误差
1. 刀具磨损机理
刀具磨损会导致工件已加工表面粗糙度上升,工件尺寸变化并超差,并且可导致切削温度上升。合理控制刀具的磨损,使刀具在正常磨损范围内工作,有利于提高工件的尺寸精度及表面质量。
刀具磨损主要是由于切削过程中前刀面、后刀面与工件、切屑表面接触和摩擦造成的。刀具正常磨损按其发生部位分为三种类型:后刀面磨损、前刀面磨损(月牙洼磨损)和前后刀面同时磨损。
刀具磨损过程包括初期磨损、正常磨损和剧烈磨损三个阶段,如图2-28所示。
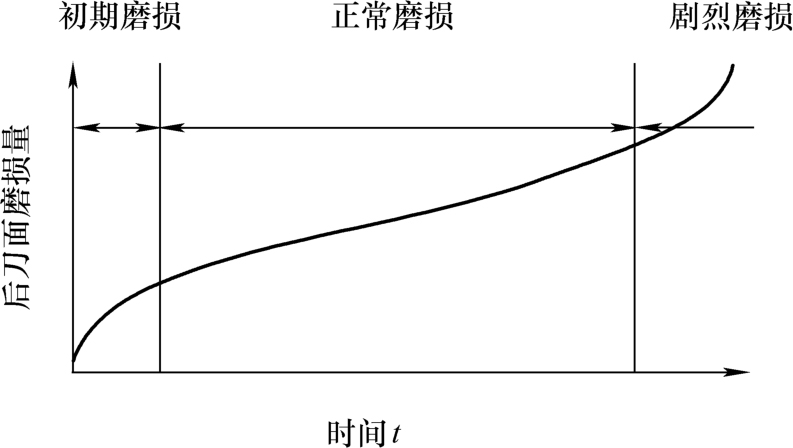
图2-28 刀具磨损过程曲线
由于刀具磨损造成的误差称为磨损误差。磨损误差随时间线性增加,磨损误差对加工时间长或批量工件的精度影响较大,而在单件短时加工(如精车)中,刀具磨损误差对工件的精度影响较小。因此,不同切削条件下,刀具磨损对加工精度的影响也不相同。
2. 刀具磨损计算
(1)刀具寿命 一把新刀从开始切削直到磨损且达到磨钝标准为止总的切削时间,或者说是刀具两次刃磨之间总的切削时间,以 T 表示。

式中, C T 为刀具寿命系数,与刀具、工件材料和切削条件有关; x 、 y 、 z 为与切削用量有关的指数。
式(2-13)中的所有系数和指数可从相关手册中查取。
(2)刀具磨损误差计算

式中, V B 为刀具磨钝标准; t 为实际切削时间。
3. 刀具磨损引起的误差元素
刀具磨损会在 X 、 Y 、 Z 三个方向产生误差,分别是 X 向误差元素 δ xw 、 Y 向误差元素 δ yw 、 Z 向误差元素 δ zw 。
2.5.2 其他误差
1. 伺服系统跟随误差
数控机床的伺服进给系统在恒速输入时,稳态情况下系统的运动速度与指令速度值相同,但两者的瞬时位置却有一恒定的滞后。如图2-29所示,伺服系统在 t 1 时刻进入稳态,实际位置与指令位置滞后一个 δ 值,该滞后值称为跟随误差。跟随误差与系统增益有关,系统增益越大跟随误差越小,但系统增益过大会造成系统稳定性能变差。
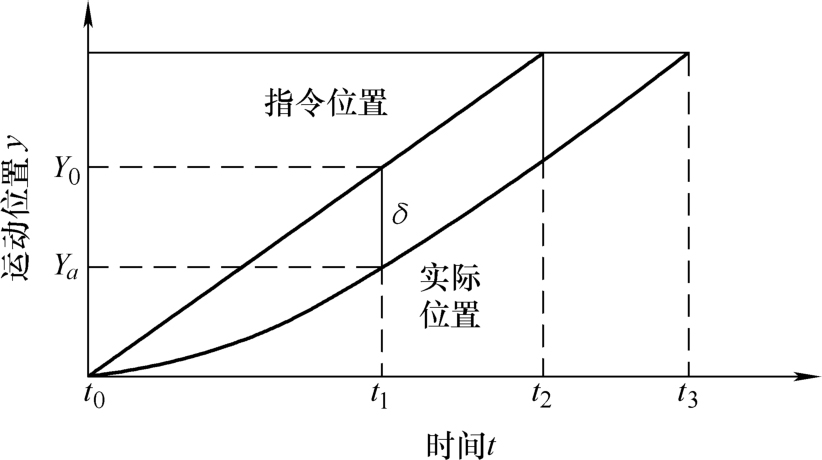
图2-29 伺服系统跟随误差
数控机床的跟随误差会引起轮廓误差,其关系如图2-30所示,由于跟随误差的存在,加工后工件的实际轮廓与理想轮廓偏离 δ ,造成轮廓误差。
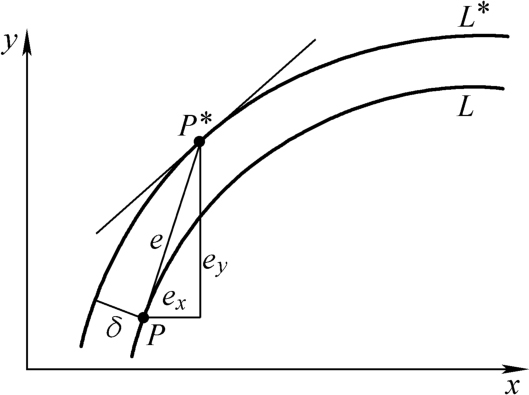
图2-30 跟随误差引起轮廓误差
L * —指令轮廓 L —实际位置 e —跟随误差 δ —轮廓误差
2. 步距误差
步距误差通常是指步进电动机运行时,转子实际转过的角度与理论步距角的差值。由于步进电动机转子转过一圈时,将重复上一圈的稳定位置,即步进电动机的步距角累积误差(转子连续走若干步时,步距角的总误差)将以一圈为周期重复出现,转一周的累积误差为零。通常步进电动机的静态步距误差在10 ′ 以内。
3. 插补算法误差
机床数控系统依照一定方法确定刀具运动轨迹的过程称为插补。也可以说,已知曲线上的某些数据,按照某种算法计算已知点之间的中间点的方法,也称为“数据点的密化”。数控装置根据输入的零件程序的信息,将程序段所描述的曲线的起点、终点之间的空间进行数据密化,从而形成要求的轮廓轨迹,这种“数据密化”机能就称为“插补”。
插补计算就是数控装置根据输入的基本数据,通过计算,把工件轮廓的形状描述出来,边计算边根据计算结果向各坐标发出进给脉冲,对应每个脉冲,机床在响应的坐标方向上移动一个脉冲当量的距离,从而将工件加工出所需要轮廓的形状。
在数控机床中,刀具不能严格地按照要求加工的曲线运动,只能用折线轨迹逼近所要加工的曲线。这种逼近所形成的误差称为插补算法误差。
4. 主轴回转误差
由于制造误差的影响,主轴轴线的运动可分解为纯径向位移(在与主轴轴线垂直的方向)、纯轴线位移(在平行主轴轴线的方向)和角位移(主轴轴线摆动)。这些位移以一定的方式综合起来就构成通常测量的径向振摆(纯径向位移和角位移的综合)与轴向摆动(纯轴向位移与角位移的综合)。
影响主轴回转精度的因素有轴承和主轴其他部件的几何精度及其装配误差,主轴转速、负载、工作条件、润滑、主轴部件的结构特性(轴承形式、支撑间的距离)、传动方式、热变形等。
5. 编程误差
由于编程时的近似运算误差、分割点坐标计算误差、插值误差、尺寸圆整误差及预求刀具轨迹的误差而引起的误差称为编程误差。编程误差的大小与其应用的具体数控机床的精度有关,也即编程误差取决于机床的分辨率(脉冲当量)。
6. 反向间隙误差
因为丝杠和丝母之间存在一定的间隙,所以在正转后变换成反转时,在一定的角度内,尽管丝杠转动,但是丝母还要等间隙消除(受力一侧的)以后才能带动工作台运动,这个间隙就是反向间隙。由反向间隙造成的误差称为反向间隙误差。
2.5.3 误差元素表及其应用
1. 误差元素表
由刚体系统理论可知,刚体的独立坐标数目为6个,即刚体有6个自由度。各刚体之间用“铰”连接,从而得到多刚体系统。数控机床是由多种构件组成的精密复杂系统,在研究数控机床这一复杂系统时,可以将构成系统的各构件简化为刚体,从而得到数控机床的“多刚体系统”。多刚体系统各独立刚体通过铰连接,即引入了约束,限制了刚体的自由度,而数控机床误差研究是从各刚体及铰的微变出发,也就是说,刚体及铰在内外因素的影响下会沿6个自由度方向产生变形,即刚体会在6个自由度方向产生误差。
由误差元素分析可知,数控机床的误差元素(轴间误差除外)具有某种内在规律,即都表现为沿坐标轴的移动误差
δ
uv
和绕坐标轴的转角误差
ε
uv
(其中第一个下标表示误差方向,第二个下标表示坐标轴的运动方向),只是误差源不同。鉴于此,数控机床的误差元素可以表示为
 、
、
 ,其中上标
S
(Source)表示误差源,而把
δ
uv
、
ε
uv
称为基本误差元素。表2-2为数控机床误差元素表。
,其中上标
S
(Source)表示误差源,而把
δ
uv
、
ε
uv
称为基本误差元素。表2-2为数控机床误差元素表。
表2-2 误差元素表
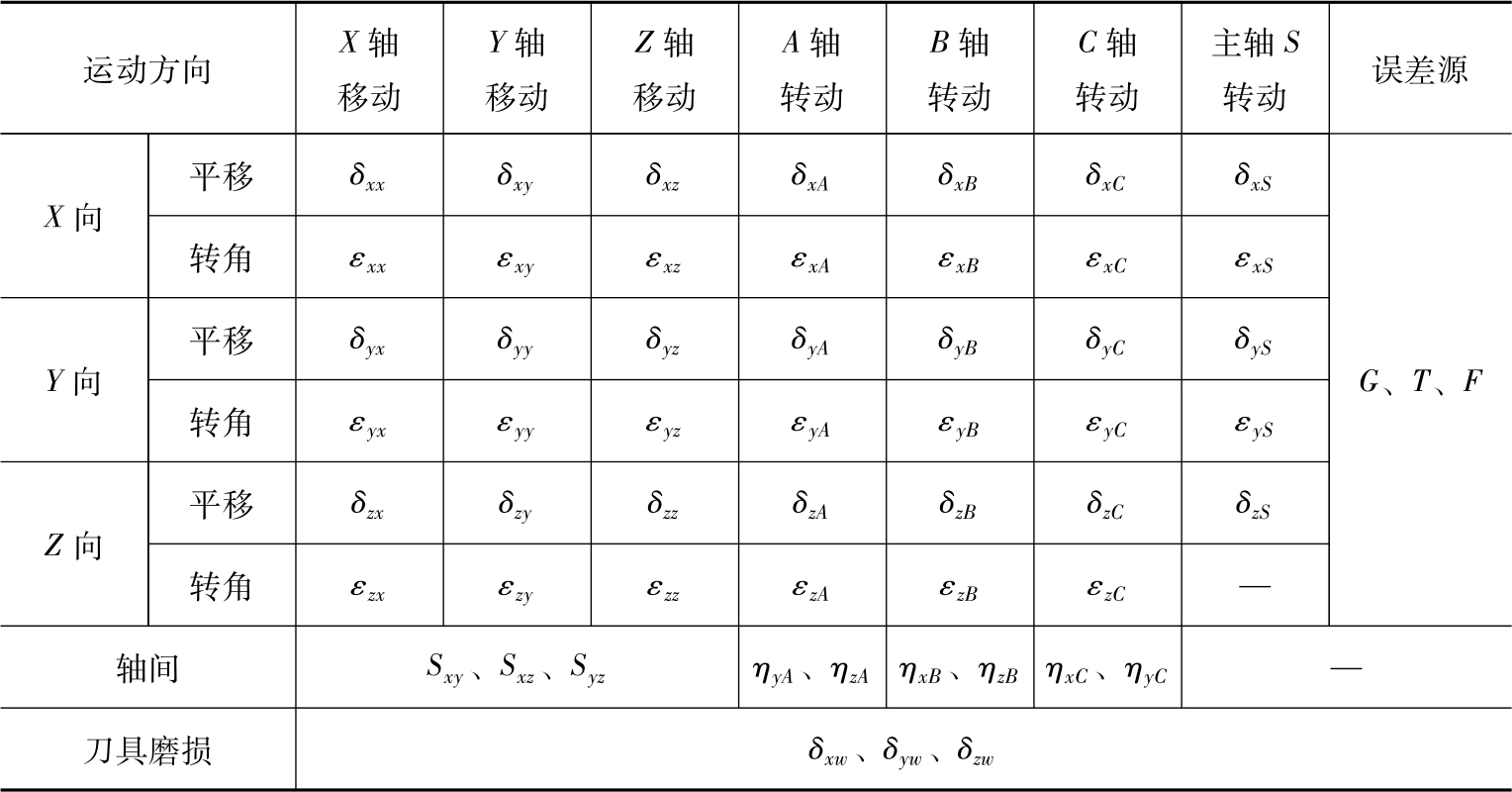
表2-2中,误差源 G (Geometric error)表示工艺系统几何误差, T (Thermal error)表示加工过程中产生的热误差, F (Force error)表示加工过程中产生的力误差。
2. 误差元素表的应用
下面以图2-31所示三轴加工中心为例说明误差元素表的应用。其运动部件包括主轴、 X 工作台、 Y 工作台和 Z 工作台,因此取误差元素表中 X 轴移动、 Y 轴移动、 Z 轴移动、主轴 S 转动四列基本误差元素,则加工中心误差元素见表2-3。
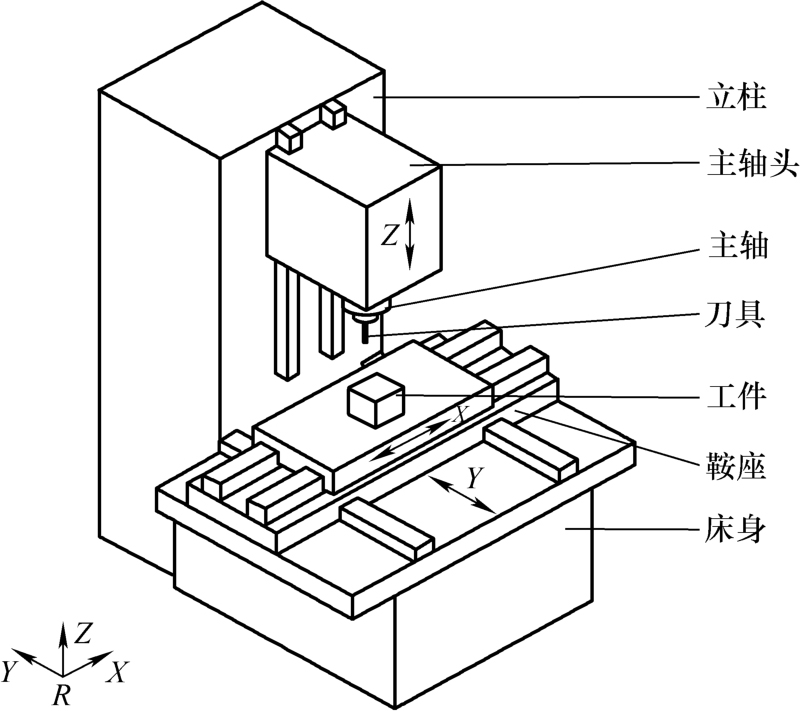
图2-31 数控加工中心
表2-3 加工中心误差元素
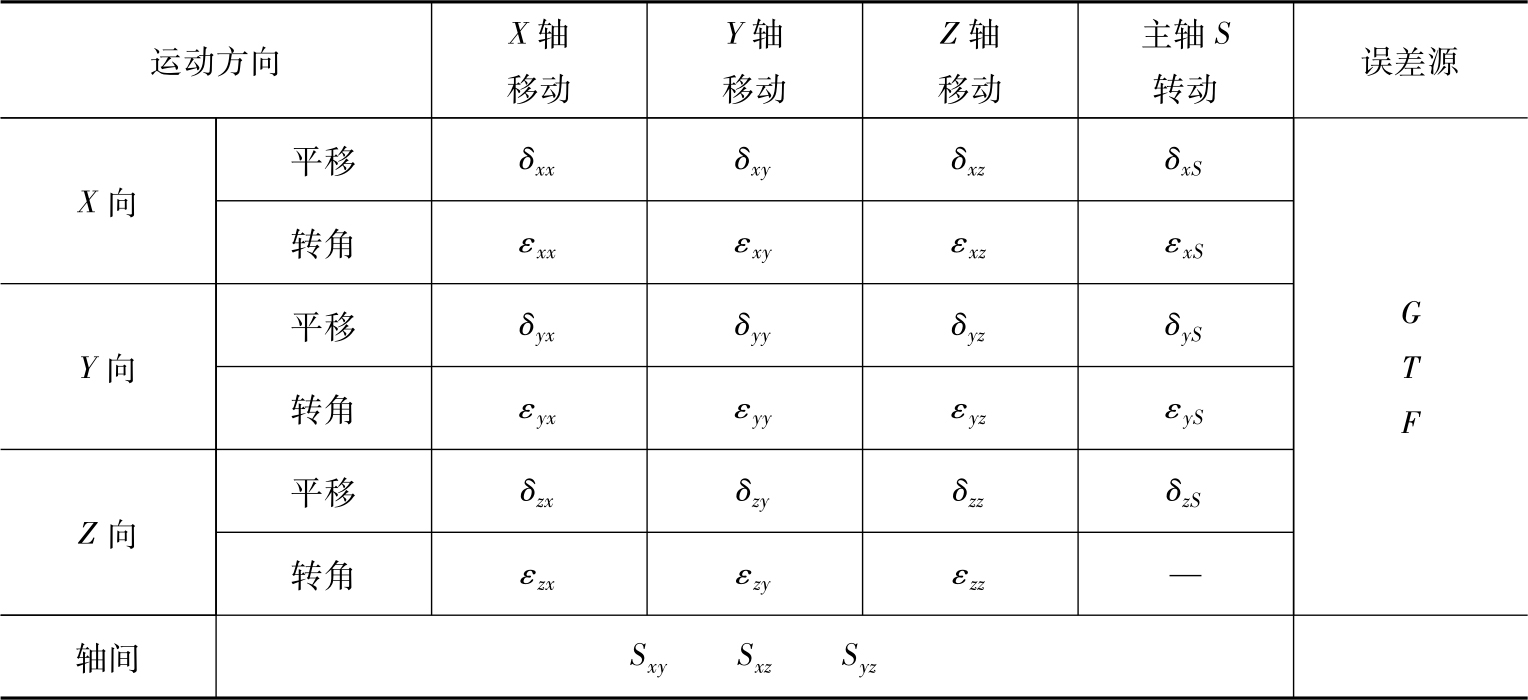
由表2-3可知,加工中心共有26个基本误差元素,引入误差源
G
、
T
、
F
,则该加工中心的误差元素为





 共78个误差元素。
共78个误差元素。


