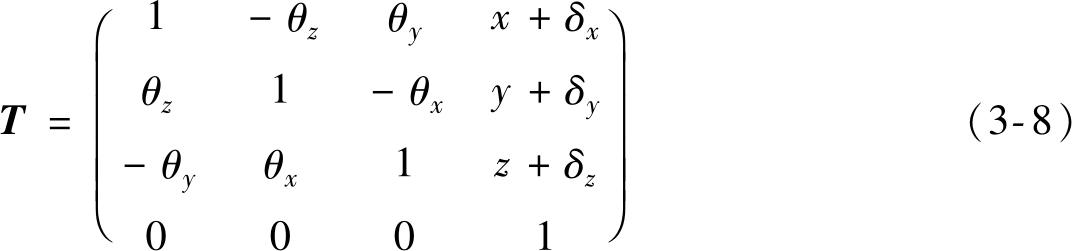3.1 齐次坐标变换
1. 齐次线性变换
设有序数组( x , y , z )及与之对应的有序数组( x′ , y′ , z′ ),满足(齐次)关系:
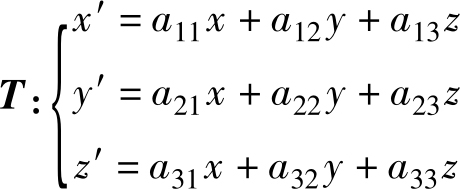
称 T 是把有序数组( x , y , z )变到( x′ , y′ , z′ )的一个齐次线性变换。有序数组( x′ , y′ , z′ )称为在变换 T 下的( x , y , z )的像,( x , y , z )则称为( x′ , y′ , z′ )的原像。方阵:
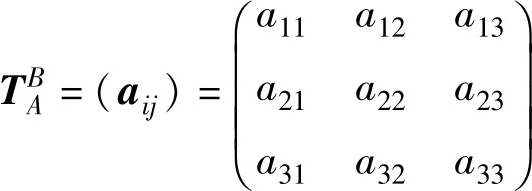
称为齐次线性变换 T 的方阵或齐次线性变换矩阵。
若有序数组( x , y , z )及与之对应的有序数组( x′ , y′ , z′ )分别为两个空间坐标系 A 和 B 中的两个位置坐标,则称 T 是把坐标系 A 中的位置坐标( x , y , z )转换到坐标系 B 中的位置坐标( x′ , y′ , z′ )的一个齐次坐标(线性)变换。
2. 二维齐次坐标变换
如图3-1所示,设 P 点在原坐标系 O A X A Y A 中的坐标值为( x A , y A ),当坐标系 O A X A Y A 移至新坐标系 O B X B Y B 后,则 P 点在新坐标系 O B X B Y B 中的坐标值( x B , y B )与( x A , y A )的关系可表示为
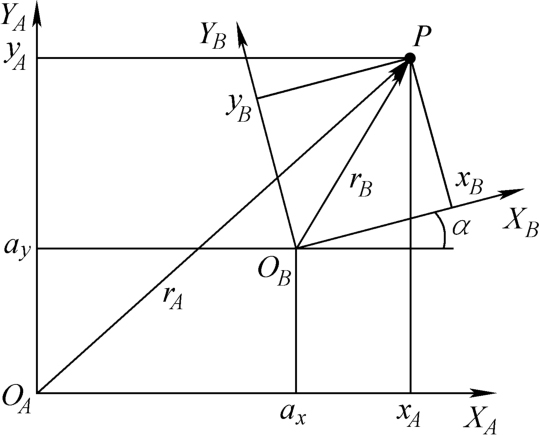
图3-1 二维坐标变换
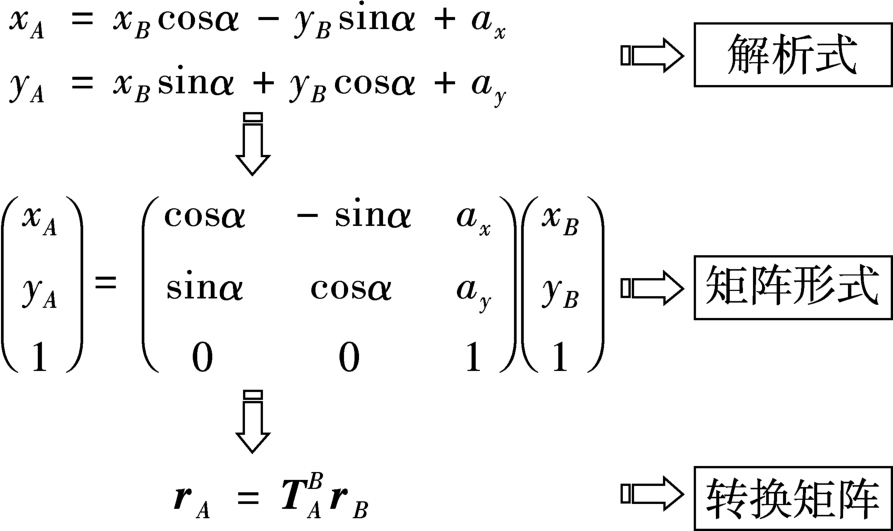
式中,
r
A
、
r
B
表示向量;
 表示坐标变换矩阵。
表示坐标变换矩阵。

3. 三维齐次坐标变换
如图3-2所示,设 P 点在原坐标系 O 1 X 1 Y 1 Z 1 中的坐标值为( x 1 , y 1 , z 1 ),当坐标系 O 1 X 1 Y 1 Z 1 沿 X 1 轴平移 x 至新坐标系 O 2 X 2 Y 2 Z 2 后,则 P 点在新坐标系坐标系 O 2 X 2 Y 2 Z 2 中的坐标值( x 2 , y 2 , z 2 )与( x 1 , y 1 , z 1 )的关系可表示为
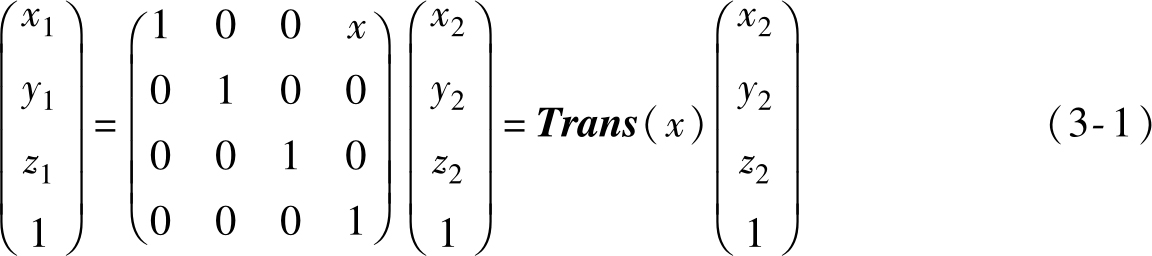
式中, Trans ( x )表征沿 X 1 轴平移的平移矩阵。
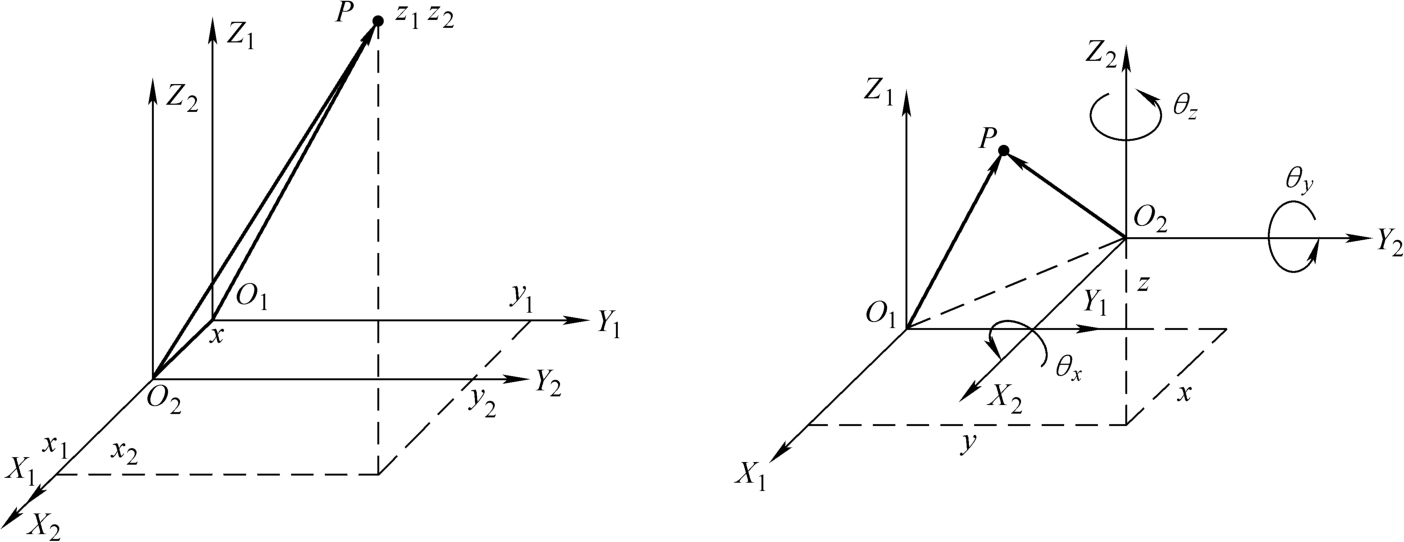
图3-2 坐标系的坐标变换
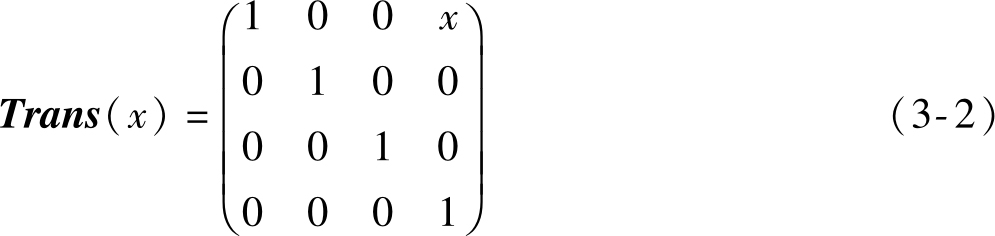
类似地,沿 Y 1 轴和 Z 1 轴的平移矩阵分别为
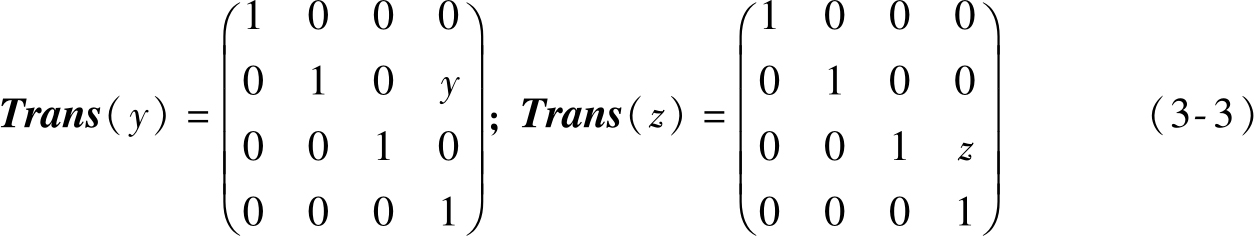
若坐标系 O 1 X 1 Y 1 Z 1 绕 X 1 轴旋转 θ x 后成为坐标系 O 2 X 2 Y 2 Z 2 ,则
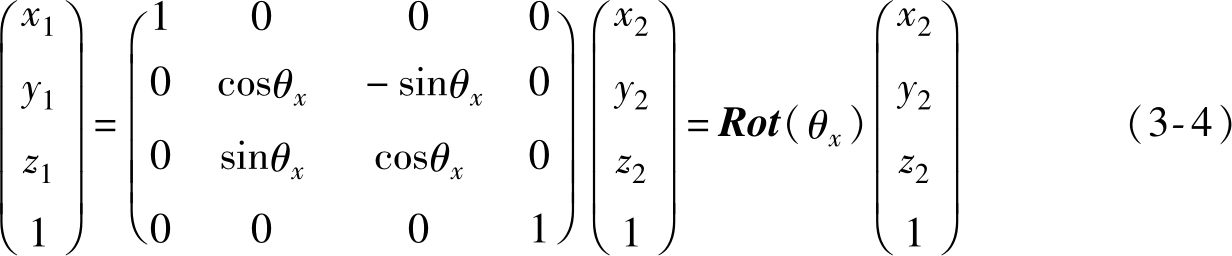
式中, Rot ( θ x )为绕 X 1 轴的旋转矩阵。
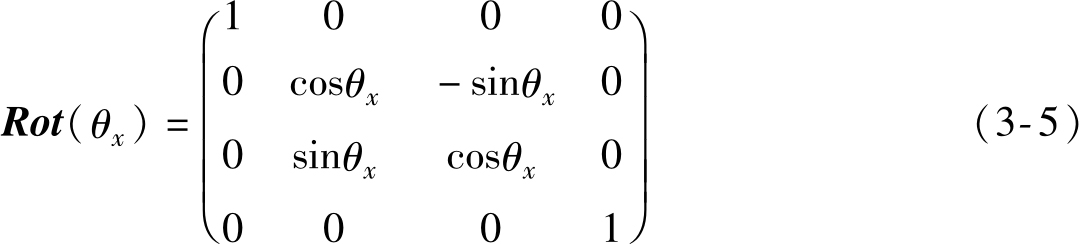
类似地,绕 Y 1 轴和 Z 1 轴的旋转矩阵可分别表示为
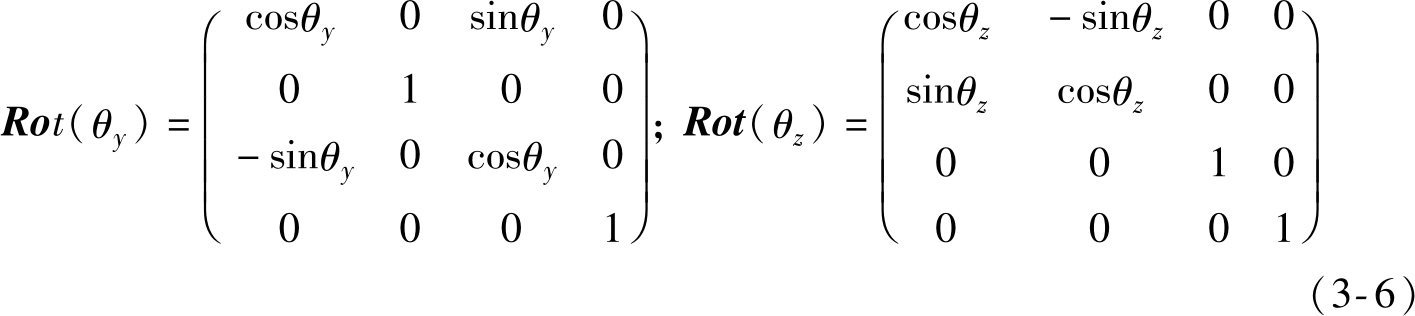
在坐标系的坐标变换中,若坐标系 O 1 X 1 Y 1 Z 1 先分别沿 X 1 、 Y 1 和 Z 1 轴平移 x 、 y 和 z ,再分别绕 X 1 、 Y 1 和 Z 1 轴旋转 θ x 、 θ y 和 θ z ,则表征 O 1 X 1 Y 1 Z 1 经上述平移、旋转后转换到新坐标系 O 2 X 2 Y 2 Z 2 之间关系的齐次坐标变换矩阵为
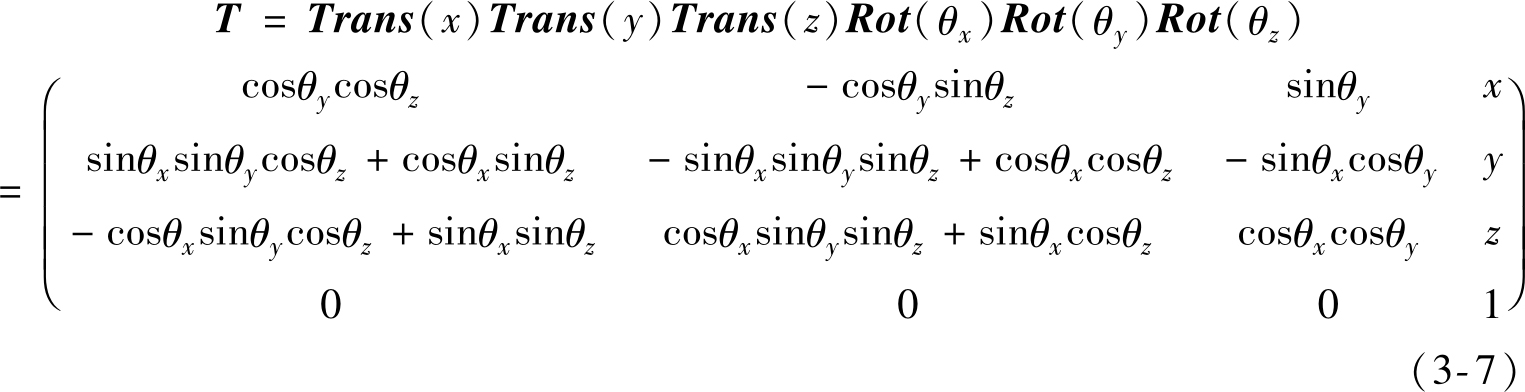
当旋转角度 θ x 、 θ y 和 θ z 非常小时,有sin θ x ≈ θ x 、sin θ y ≈ θ y 、sin θ z ≈ θ z 、cos θ x ≈1、cos θ y ≈1、cos θ z ≈1。当平移 x 、 y 和 z 分别有误差 δ x 、 δ y 和 δ z 时,如忽略二阶以上微量,可将式(3-7)齐次坐标变换矩阵简化为