1.3 数控机床误差补偿技术研究的历史、现状和发展趋势
1.3.1 数控机床误差补偿技术研究的历史
从误差源的角度来说,数控机床误差补偿技术研究的历史主要围绕各种误差元素进行,其中包括机床几何误差补偿、机床热误差补偿、机床力及振动误差补偿、刀具磨损引起的误差补偿、其他误差补偿以及数控机床多误差元素综合补偿等。从误差补偿手段来说,数控机床误差补偿技术研究的历史是从误差补偿系统的研发和提高数控机床精度两方面进行的,其中误差补偿系统的研发得到各国研究人员及专家的公认,并已经部分应用于数控机床,为推进数控技术的持续发展做出了不菲贡献。
1. 机床几何误差补偿历史
对于几何误差的补偿,首先需要确定数控机床的几何误差元素。根据一个物体在空间有六个自由度,物体在运动时会在六个方向上产生误差,可以得出三轴数控机床具有18个运动误差,而由于三轴机床的三个坐标轴两两垂直,在运动时会产生3个垂直度误差,即三轴数控机床具有21个几何误差元素,这些误差元素对总误差的影响可根据各自的贡献取舍。随着检测技术的不断发展及激光干涉仪等高精度测量仪的不断发展,数控机床几何误差的检测精度及效率也越来越高,这为数控机床几何误差模型的建立提供了技术支持。
数控机床几何误差的补偿,通常是先采用激光干涉仪 [1,136,137] 、球杆仪 [2,3] 、平面光栅 [4] 等检测仪器测量数控机床的几何误差 [5~9] ,然后进行建模补偿 [10~17] 。常用的机床几何误差测量方法是体对角线测量及分步体对角线测量 [18~22] ,分步体对角线测量是在现有的机床体对角线激光测量方法的基础上,将每一斜线单步测量运动分解为空间三个方向的分步测量运动,再根据向量分析算法,通过分步测量机床工作空间的四条体对角线快速得到9个位置误差和3个垂直度误差元素。此外,J. P. Choi [23] 等人使用接触式探针在线测量一台三轴加工中心的定位误差,运用多项式方程建立起定位误差模型,实现了定位误差的预测,并用光阶规对预测结果进行了验证。Fung [138] 等人利用8测头方法对导轨直线度、俯仰角度及滚转角度进行测量。上海交通大学胡德金 [148] 提出了一种基于图像识别的球度误差判别方法和在位误差补偿方法,根据球面上形成的磨削迹线形貌特征来判别球面的形状误差,进而判断磨削主轴中心线与球体旋转中心线之间的几何偏差大小。Lee [149] 采用数学方法消除了用激光干涉仪测量三轴机床垂直度过程中阿贝误差对测量结果的影响。除上述测量方法外,还包括激光跟踪仪测量 [152] 、22线、15线、14线、13线及9线测量 [153] 。近年来,基于集成白光共焦探针的轮廓测量仪实现了在位测量技术 [154~158] 。
在进行几何误差检测后,通常要建立几何误差模型,最初是以刚体运动学及相关数学理论为依据,通过对几何误差的分析和计算来建立几何误差的数学模型。近来,常用的建模方法有齐次坐标变换、神经网络、多元回归、多体系统理论、多体动力学方法、最小二乘算法、遗传算法等 [24~28,139,150,151,159,160] 。Ferreira和Liu [29] 提出了一种基于刚体运动学和小角度误差假设的三轴机床几何误差的解析二次型模型,为了简化分析,两种直线度误差在单一变换矩阵中被认为是两个角度误差的相关变量,角度误差成分假定为线性函数;使用这种二次型模型的优点在于机床的主要误差可以直接表达为参数形式。Kurtoglu用运动学模型补偿了铣床的空间误差,该模型包括了18个运动副误差,但不包括垂直度误差。Chen [30] 等人在刀具与工件之间相对位移误差的运动学建模中,去除了刚体运动的假设,可对非刚体误差进行补偿,而且,通过标准齐次线性坐标变换方法建立了几何和热误差两者的模型,该模型考虑了32个误差成分,而不是传统的21个误差成分,使得基于该模型的误差补偿获得了更好的效果。Christopher. D [31] 运用激光球杆仪(LBB)获得了机床的几何误差信息,建立了误差模型,并对误差补偿结果进行了评价。其结果表明,通过软件误差补偿的方法可以提高机床的加工及测量精度。Anjanappa [32] 研发了一种运动学模型可以合成立式车削中心所有几何误差。
近年来基于几何误差敏感性分析能够量化各几何误差项对三轴机床加工精度的影响,傅里叶幅值敏感性分析(Fourier amplitude sensitivity test,FAST)和Sobol方法是两种典型的基于方差分解法的全局敏感性分析方法 [161,162] 。Cheng [163,164] 等首先采用了扩展型傅里叶幅值敏感性分析法对立式加工中心进行敏感性分析,计算了高维非线性的机床误差模型中几何误差项之间的耦合效应,并分析出立式加工中心中最为关键的几何误差项;之后又进一步用Sobol方法研究了该加工中心的18个几何误差项对加工精度的影响关系,并且成功识别出了对机床加工精度影响最大的几何误差项。
Daisuke Kono [33] 在分析运动误差模型的基础上,提出直线度误差补偿模型,利用微动装置对 Z 轴运动误差进行补偿;该方法在平面铣削中能有效提高平面度。M. Y. Cheng [34] 提出一种用于基于DSP的多轴运动控制系统的实时NURBS指令发生器,该方法能够有效地提高非均匀有理B样条曲线的加工精度。R. Ramesh [35,36] 综述了目前已有的跟踪和轮廓误差的补偿方法,分析了比例控制P、比例微分控制PD、比例积分微分控制PID、零相位误差跟踪控制ZPETC、扩展带宽零相位误差跟踪控制EBZPETC等伺服控制器的优缺点;指出传统算法是基于反馈原理的,该方法具有补偿的滞后性及反馈精度不稳定的缺点;由于数控机床的参考轨迹是预知的,基于此的前馈控制可有效提高加工精度;他同时指出提高单轴的精度并不能有效保证机床总体性能的提高,但是在机床的精度补偿中还是有益的。
南京理工大学和南京航空航天大学 [37] 提出了一种模糊自学习误差补偿方法,根据伺服机构的位置误差和位置的变化率,利用模糊规则和推理得出位置误差初始校正值,采用自学习、自校正技术生成位置误差校正表,该方法成功应用于开环数控系统的位置误差补偿。
在国家自然科学基金和国家863计划项目的支持下,华中科技大学 [38] 开展了对数控机床几何误差补偿以及基于切削力在线辨识的智能自适应控制的研究,取得了一些成果。开发了一套简便快速的数控机床误差检测、评价与补偿系统,应用此系统不仅能大幅度提高误差检测的效率,而且能显著提高数控机床精度;提出一种在工业现场进行单轴高精度位置误差的测量系统,使用步距规,可以用来代替激光干涉仪进行轴线位置的高精度标定;安装简单,操作容易,通过该方法,可以使机床实现“软”升级。
北京工业大学 [39] 使用多体系统理论运动学编写出三坐标数控机床通用几何误差补偿软件,该软件在北人印刷集团实地实验取得明显的误差补偿效果。
天津大学 [40] 提出了基于多体系统理论的数控机床运动误差模型、几何误差参数综合辨识模型及相应测量技术,使用9线位移误差及直线度误差测量,可准确辨识数控机床整个工作区间内的全部21个几何误差参数;在三坐标立式加工中心上进行软件误差补偿实验,并在坐标测量机上检验。结果表明,建模方法具有较强的实用性。
上海交通大学 [41] 提出了一种基于FANUC数控系统的外部坐标原点偏移功能的补偿方法,该方法利用自行研制的外部补偿器与机床数控系统进行交互,可使机床的几何误差以及随温度变化的热误差得到较好的实时补偿。实验证明,此补偿过程方便、经济,补偿效果好。
随着五轴数控机床的问世,多轴机床几何误差的检测及补偿相应产生 [42~44] 。Lin和Ehmann [45] 提出了一种直接空间误差分析方法,可以评价多轴机床工作的位置和方向误差,他们的研究工作提供了对任意构造的机床自动产生误差合成模型的基础。W. T. Lei [46] 等提出了用3D探头检测五轴机床空间精度的方法,该方法摆脱了以往不能检测五轴机床转动轴误差的局限,该装置可用来测量所有和位置有关的误差,但不能检测机床的热误差;检测时,将3D探头安装在机床的主轴上,和探头相连的机座安装在转台上。采用齐次坐标变换的方法建立探头相对于机座的运动链(包含了所有的位置误差项),这样当探头按照特定的检测路线运动时,就可以得到一系列检测数据,反向求解矩阵得到各个原始的误差项;之后,W. T. Lei [47] 等以此误差辨识方法为基础,建立了五轴机床的误差预测模型,并把该模型植入机床控制系统,通过开发的补偿系统实现了五个自由度的补偿。
北京交通大学李北松 [140] 设计了一种基于激光技术的五自由度同步测量系统,该系统可同时检测直线导轨的五自由度方向上的误差。在测量范围1m内,直线度误差可达到1μm,角度误差的测量分辨率可达到0.3″。崔存星 [145,146] 在此基础上开展了激光外差干涉结合激光光纤准直技术的六自由度测量系统研究,实现了直线轴系运动过程中六个几何误差项的同时测量。
Y. Y. Hsu [48] 提出了五轴机床几何误差的解耦补偿法,该方法主要通过四步:①计算 A 轴补偿角,②计算 C 轴补偿角,③计算由 A 、 C 轴补偿角引起的线性误差,④计算所有线性轴的综合补偿值,然后通过修改NC代码实现补偿。Hang &Ding [143,144] 通过球杆仪分别以先乘旋转轴的齐次误差矩阵和后乘旋转轴的齐次误差矩阵两种情况对旋转轴的几何误差辨识结果的影响做了深入研究。通过旋量理论建立没有考虑几何误差 [145] 和考虑所有几何误差影响 [146] 的五轴机床的运动方程。上海交通大学项四通 [147] 等人通过旋量理论建立综合几何误差五轴机床的运动方程,且引入了误差关节的概念,同时上海交通大学补偿团队提出了五轴解耦补偿技术,该方法解决了多轴机床误差相互耦合的问题,为多轴机床误差补偿提供理论依据。
2. 热误差补偿历史
最早发现机床热变形现象并进行研究的国家之一是瑞士。1933年,瑞士通过对坐标镗床进行测量分析后发现,机床热变形是影响定位精度的主要因素。从此,在各国展开了数控机床热误差的研究与补偿。
研究初期,各国学者对机床热变形的研究重点放在改进机床热特性上,企图用解析和数字(有限元)方法来计算机床结构的热膨胀与变形。研究人员使用FEM进行机床热变形计算和机床优化设计 [49,50] ,期望通过改进机床结构的方式来降低机床热误差;然而,由于机床结构及制造的限制,单靠改善机床结构无法有效补偿数控机床在加工过程中产生的热误差。
于是,各国研究者将热误差的研究转向热误差建模补偿。最初的热误差补偿采用三角函数关系进行,由于该方法计算复杂,一不小心就会出错,进而采用向量表达方法,并成功应用于建立三轴坐标镗床的空间误差模型;之后又用多维误差矩阵模型来提高三维坐标测量机的测量精度,并成功用于坐标测量机上 [51] 。热误差补偿技术在三维坐标测量机上的成功应用,有力地推动了误差补偿技术的发展。
随着热误差补偿研究的不断进展,各种相关理论随之诞生。日本学者提出了“热刚度”的概念,确立了热变形研究理论向控制机床热变形的CAD和CAM方向发展 [52~54] ,并取得了一定效果。M. Weck [55] 等提出了机床热模态分析理论,并把热模态和振动模态分析进行了比较。浙江大学 [56] 根据热弹性理论推导了刀具的热变形计算公式,对车刀热变形误差进行了微机补偿,取得了良好的效果;之后,该校 [57] 又建立了精密机械热模态理论,提出了机床热系统特征值概念,并以“热敏感度”和“热耦合度”新概念和定量分析方法来描述复杂的机床热系统。上海交通大学 [58~61] 通过对机床热特性测定、分析和研究,得出了机床温度场分布图,并进行了一系列的误差补偿研究工作,取得了一定的成效。
在全面分析机床热特性的基础上,建立热误差数学模型是进行热误差补偿的关键。1984年,在美国威斯康辛大学召开的国际生产工程研究会(CIRP)第三十四届年会上 [62] ,会议主席威士荷姆在发言中强调:研究工作不能简单地靠直接经验,而要靠科学的方法。对于机床热变形规律,要通过精确测试及分析,进而探索机床热变形的规律和机理以获得有效的补偿。之后美国学者M. A. Donmey等提出主轴热变形误差通用模型:
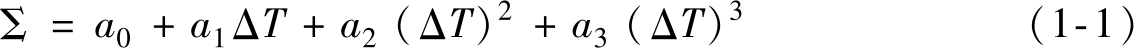
式中, a i ( i =0,1,2,3)为转化系数;Δ T 为温升。
式(1-1)为热误差的补偿建模提供了一条思路,它是幂函数的近似逼近。
Raghunath等人在全面分析数控机床精度的热影响基础上,理论推导得出:在准静态条件下,机身某瞬时热变形取决于该瞬时机身的温度;进一步分析表明:热对机床精度的影响可由机床结构上的一些特征点温度来预测。这一理论为热误差温度场的检测及温度传感器的优化布置提供了理论基础。德国学者W. Schafer [63] 在机床热变形模型的基础上,确立了机床工作过程中相对弹性位移最适当的测量点,建议在机床的驱动电动机上测量温度。上海交通大学在对数控机床主轴热模态分析的基础上,提出了温度传感器的优化布置策略 [64] 。
在热误差理论研究的基础上,各种热误差补偿方法如雨后春笋般涌现。日本学者 [65] 首先提出了一种主轴热变形补偿方法,即预先求出温度和热变形关系式,通过测试系统检测实际加工时特定点的温度,利用温度和热变形关系式,通过机床工作台的移动进行补偿。日本东京大学 [67] 根据智能制造新概念开发了由热作用器主动补偿综合误差的新方法,并在加工中心上予以实现;该加工中心包括了神经网络智能控制器,力、温度、位移传感器及失效安全机构,加工中心立柱下部有一段是可控可变结构,在其外表面安装了16个加热器,内表面安装了16个致冷器,在立柱12个位置上安装了变形传感器,采用了矩阵法和神经网络逼近方法主动补偿加工误差,测试表面最大加工误差可被控制在10μm以内。日本学者还进行了液体静压主轴热变形在线补偿的研究工作并取得一定成果 [68] 。
Janeczko [69] 用两个温度传感器采集数据,对主轴做软件补偿,该系统每10s循环一次,它可以补偿95%的原始膨胀误差,并研究和计算了轴承温度和主轴膨胀之间的热延迟;这一技术在大型卧式钻床和立式磨床的主轴热膨胀补偿中均获很好效果。日本学者千辉淳二 [70] 论述了机床的模型化、温度控制方式的模型化、内部热源的模型化和外部热源的模型化,在仿真方面还阐述了机床与热负载的模型、最优控制等;松尾光荣 [65] 研究了加工中心的温度分布及测量并对该加工中心进行了热变形补偿,详细介绍了温度分布-加工部位热变形的数学模型、试验方法及分析结果,所获得的模型可根据机床关键温度点的测定来实现坐标轴自身变形的预测及误差补偿。新加坡国立大学的R. Ramesh [66] 等研究了变操作条件下热误差的测量和建模,并用混合贝叶斯网络成功建立了热误差数学模型。
美国学者Hong Yang [71] 等从动态特性的角度对机床系统进行了热弹性分析,指出伪滞后效应是造成传统热误差模型鲁棒性差的主要原因,并建立了系统动态热误差模型。此后,他们又使用动态神经网络的方法对热造成的非线性、非稳态的误差进行了建模,并设计了一种系统模型自适应法,利用迭代的方法不断修正模型系数,以期达到热误差模型的高鲁棒性。美国密西根大学吴贤铭制造研究中心 [72] (S. M. Wu Manufacturing Research Center)开发了基于PC的加工误差神经网络实时补偿系统,用以弥补工业CNC控制器的误差补偿能力。其工作原理为:机床三个工作台的位置由相位编码器输入和数字量输出板(Q/D板)获得,静态几何误差被存在数据库中,虽然这些误差在一段时期里相当稳定,但由于长期发生变化的机床磨损和材料稳定性等原因,需周期性的更新;动态热误差由安装在机床各部位上的23个热电偶通过人工神经网络模型进行预测,系统补偿软件由C语言编制。该补偿方法的一个优点在于,由微机补偿控制器通过一个数字I/O口发出二进制的补偿值给CNC中的PMC板,可无需对原CNC伺服系统的硬件做任何改动,最后通过实时控制刀架的附加进给运动来完成误差实时补偿。
赵大泉等 [73] 针对传统补偿策略算法复杂、成本较高且通用性不强等问题,提出了一种基于自组织原理的主轴热误差补偿策略,它只需根据对主轴热倾斜状态的定性测量结果即可进行定量误差补偿,从而可以大大降低对误差测量精度的要求及测量成本,同时各补偿值间的协调关系根据自组织原则自动建立,简化了补偿算法,经过对某型加工中心主轴热误差进行的自组织仿真补偿,其主轴热倾斜误差减小了92%以上,热漂移误差减小了46%以上。
上海交通大学 [74] 基于机床热变形误差的产生机理及其表现形式的复杂性,综合时序分析方法建模和灰色系统理论建模的优点,研究了一种智能混合预测模型,并将该模型应用于一台数控车削加工中心的热误差趋势预测。结果表明,混合预测模型预测精度高于时序分析模型和灰色系统模型,其优异的预测性能可使数控机床热误差的实时补偿更加有效,从而大大提高了机床热误差的补偿精度。
浙江大学 [75] 提出了基于最小二乘支持向量机进行数控机床热误差建模预测的方法。根据最小二乘支持向量机回归预测的原理,优化选择最小二乘支持向量机参数,对数控车床热误差进行最小二乘支持向量机建模,通过测量数控车床主轴温升值与主轴热变形量,将获得的数据进行最小二乘支持向量机建模训练,以建立机床热误差预测模型。实验结果表明,该模型能有效描述热动态误差。与最小二乘法建模进行比较,结果显示,基于最小二乘支持向量机的数控机床热误差预测模型精度高、泛化能力强。采用最小二乘支持向量机得到的预测模型可用于数控机床热误差实时补偿。该校还提出了机床热误差Fuzzy前馈补偿控制策略,根据热误差变化规律的模糊、非线性特性,采用Fuzzy集理论设计前馈补偿控制器,仿真研究表明补偿控制策略取得了良好的结果。
北京机床研究所 [76,77] 在一台DM7732数控线切割机上实现了热变形补偿,其补偿效果达70%。之后,该所应用专家系统对热误差进行实时补偿,仿真结果令人满意。在此基础上,该所又为XH714A立式加工中心研制了一块智能补偿功能板,通过总线将补偿板直接插入FANUC 6ME数控系统扩充槽,实现机床热误差、运动误差和承载变形误差补偿。该所提出的数控机床误差的综合动态补偿法(Comprehensive Dynamic Compensation,简称CDC)是实时补偿技术和软件技术的结合,能根据机床工况、环境条件和空间位置的变化来自动跟踪调整补偿量,并能对几何误差、热误差和承载变形误差等进行综合补偿。
中国台湾的台湾大学和台中精机公司获得资助,合作进行了“高精度工具机热变形补偿控制技术”的研究和开发,所获得的成果主要有:误差补偿单板计算机系统模组化、温度传感器最佳位置放置点研究、误差补偿单板计算机系统验证、现场快速误差检测系统等,使所研制的立式工具机的加工精度从50μm以上降低到10μm以下。
随着智能技术的发展,各种神经网络理论也运用到机床热误差建模中,大大提高了热误差数学模型的精度,使得机床误差补偿技术又进了一步。日本学者樱庭肇 [52] 采用机床的热变形信号作为伺服轴的轴向延伸量来补偿行程指令;岗田康明 [53] 通过检测机床部件的热位移量实现热误差的自动补偿,该技术可实现长时间的高精度加工;大阪机工公司 [54] (OKK)研制的TDC-FUZZY主轴头热误差补偿控制器利用模糊控制理论控制主轴头的热误差,将变化的环境温度、机床本身温度及回转时的转速等数据作为函数,自动地输入控制程序中,利用温度调节装置,精确地控制用于冷却主轴头的润滑油的供应量,从而协调统一机床与环境的温度,最大限度地抑制热误差,一天内的热误差变化量在0.02mm以内。傅龙珠 [78] 等进行了BP神经网络补偿热变形误差的研究,以CK616-1简易数控车床为试验对象,在对其热误差分析的基础上进行热误差建模,并结合改进的BP神经网络给出了具体实现的方法,对提高机床的加工精度有着极其重要的意义。
华中理工大学 [79,80] 开发了机床主轴温升和热变形在线检测及显示系统,之后又提出了一种基于神经网络辨识影响机床热误差关键点的方法,从而为机床热监控的最佳测量点及控制源位置的选择提供了新的思路及实现方法;同时也给出了各测温点热平衡时间及平衡状态时温度的估计方法,该方法基本原理为:根据各测温点温度变化及各主轴位移测量点的变化,首先利用神经网络建立测温点温度变化与位移测量点位移变化之间的关系,进而根据这种关系所确定的导数关系辨识各测温点温度变化对位移测量点位移变化的作用程度,认为作用程度大的测量点附近区域即为温度应加以控制的区域,该方法在数控机床热误差补偿应用中取得非常理想的效果。
天津大学精仪系 [81~84] 以一台JCS-018A型加工中心为对象进行了研究,在机床加工空间内的几个主要位置和各种转速下,利用多自由度测量装置直接测量主轴相对工作台的热位移,在机床的热敏感位置上布置12个测温元件,利用神经网络理论建立了热位移与各测温点温度变化之间的关系,通过加工工件验证热误差补偿效果。实验证明,尽管这台机床的热误差较小,补偿效果依然达到60%。
热误差补偿技术的不断成熟为其在企业中的应用奠定了基础 [85,86] 。美国密西根大学吴贤铭制造中心 [87] 通过新的建模及其温度布点等方法把机床误差补偿技术运用到工业生产实际,成功地开发了经济、易用的热误差实时补偿系统,并应用于美国通用(GM)公司下属一家汽车离合器制造厂的150多台车削中心,使得其加工误差降低50%~75%。国内上海交通大学联合上海睿涛科技有限公司在批量钻攻中心上开展了Z轴热误差补偿的应用。
近年来,随着电主轴技术的不断发展及转速的不断提高,热变形成为影响主轴精度的关键因素。在高速、高精密加工中,由热变形引起的误差占总误差的60%~80% [164] 。因此,解决高速、高效、高精度工作状态下电主轴的热变形成为制约其发展的一项关键技术。目前,电主轴最常用的误差补偿方法是冷却技术及热变形优化技术。常用的冷却方式包括液体冷却和空气强制对流冷却。参考文献 [165] 通过控制制冷液的温度确定切削液的流量及冷却系统的最小换热面积,将定子温升控制在14℃。参考文献 [166] 通过分形理论设计了一种树状冷却装置以控制制冷量的分配,比传统的螺旋槽冷却装置具有更低的压降和更均匀的温度场。参考文献 [167] 研究了风速对电主轴温度的影响,为空冷电主轴的优化设计提供依据。参考文献 [168] 提出一种基于功率匹配的电主轴单元冷却策略,克服了电主轴冷却策略对主轴发热和散热的不平衡问题。除液体和气体冷却外,参考文献 [169] 利用环路热虹吸管实现电主轴轴芯冷却,解决了“动密封”问题对电主轴轴芯冷却的困扰。热变形优化是将温度场非对称结构改为相对均匀温度分布结构,通过对称热变形提高电主轴精度。参考文献 [170] 提出热平衡法,可在不改变机床结构的前提下达到改善精度目的。参考文献 [171] 应用CAE技术及田口法对数控车床主轴头进行优化设计,大大降低了开发时间和成本。参考文献 [172] 采用碳纤维的热缩特性抵消电主轴的热变形。
3. 多误差综合补偿历史
通过对各误差元素的分析,研究人员发现数控机床的各误差元素相互关联,相互影响,特别在多轴数控机床中,位置误差与姿态误差存在耦合,这样仅对单一误差元素的补偿很难大幅度提高数控机床的加工精度。各国学者进而开始对多误差综合补偿进行研究。多误差元素综合补偿大幅推动了数控机床误差补偿技术。
在多误差元素综合补偿中,首先进行的是热误差与几何误差的综合补偿。Donmez [88] 等人推导了车床的广义误差合成模型,该模型考虑了几何误差,也考虑了热误差,实现了数控机床多误差元素的综合补偿。之后,A. C. Okafor [89,90] 完成了三轴机床的几何和热误差联合建模,采用齐次坐标变换和基于刚体运动学及小角度假设条件建立该机床的几何和热误差综合数学模型,实现了三轴数控机床多误差元素综合补偿。为了确立不同温度下机床几何误差的变化情况,美国Michigan大学Jun Ni教授指导的博士生Chen Guiquan [91] 做了有益的尝试,运用球杆仪(Double Ball Bar—DBB)对三轴数控机床不同温度下的几何误差进行了测量,建立了快速的温度预测和误差补偿模型,并对由温升引起的几何误差的变化进行了补偿。
在成功进行热误差和几何误差综合补偿的基础上,其他多误差元素的综合补偿相继出现 [92] 。Chana Raksir [25] 提出了包含有力误差的三轴数控铣床的误差模型并进行了补偿,该方法综合考虑几何误差和力误差的影响,通过神经网络实现误差建模和补偿。加拿大McMaster大学 [62] 智能机器及制造研究中心开发了五轴加工误差补偿的神经网络策略,采用仿真数据和实测数据对神经网络进行训练建模,有效地补偿了由温度和结构磨损产生的加工误差。Soons [93] 等人提出了一种建模方法,可以得到包含旋转轴在内的多轴机床的误差模型。
Myeong-Woo Cho [94] 提出了基于在线测量(OMM)和神经网络多项式(PNN)的综合加工误差补偿方法。该方法主要为平头铣刀铣削加工提供一个在线测量实时补偿的误差补偿方法,有效提高了综合加工精度,但该方法在线测量精度及可靠性有待提高。
4. 其他
引起数控机床的误差有很多,从误差源及各误差元素对数控机床加工误差的贡献分析,主要的误差源包括几何误差、热误差和力误差,这三类误差占总误差的70%~90%,是影响数控加工精度的主要因素。而其他误差主要包括刀具磨损引起的误差、运动误差、伺服误差、插补算法误差等。对于其他误差的研究,各国学者也先后相继展开。
切削力误差的补偿是近来才出现的,在最初的误差补偿研究中,各国学者们主要针对的是精密及超精密加工,并且假定在普通数控加工中,在精加工阶段由于切削用量较小,由切削力引起的误差可以忽略,并且假定精加工可以完全消除之前加工的切削力累积误差。然而随着高速加工和高效切削的产生,由切削力引起的误差变得不容忽略,因此,切削力误差的研究开始逐渐提上日程。
最初的切削力误差补偿是应用经典指数公式进行的,通过对指数公式中相关修正系数的实时修正,实现切削力误差的补偿。然而,由于经典指数公式的精度问题,限制了其补偿的效果。随后开始进行实时检测切削力来实现力误差的补偿,切削力的检测方法主要通过直接检测和间接检测两种手段实现 [95~97] 。常用的直接检测方法是通过测力仪等力传感器来完成切削力的检测,其优点是检测精度高并可实现实时检测,缺点是需要改动机床的结构,并且安装调试复杂。间接检测法是通过检测电动机电枢电流来实现切削力的转换,其优点是检测方便,不用改动机床结构;缺点是检测的实时性不够,且检测精度依赖于诸多影响因素。对于由切削力引起的误差,主要通过位移传感器来检测。后来,人们建立切削力与力误差的数学模型,通过软件或补偿器进行误差补偿。
在此理论基础上,各种建模补偿方法先后出现。S. Ratchev [98,99] 提出了低刚度薄壁零件切削力及切削变形的预测和补偿方法,并且建立了柔性力学模型来补偿切削力引起的误差。该方法应用柔性理论建模,预测补偿切削力引起的误差,并且假定刀具变形可以忽略。而在实际加工中,刀具的变形是不能忽略的,因此S. Ratchev在考虑零件挠度及刀具变形的基础上修正了上述补偿方法,提出了自适应柔性力学模型,该模型可有效预测并补偿由切削力引起的误差。试验结果表明,补偿效果理想。Ruey-Jing Lian [100] 提出了一种基于灰色预测系统的模糊逻辑控制方法,该方法在改装的车床上实现了常力切削,该方法主要是控制切削过程中的切削力,从而提高切削效率并且有效减小了刀具的磨损和破坏。Armando_Italo Sette Antonialli [101] 分析了钛合金铣削中切削力与振动的相互关系,指出应用大的主偏角和高的振动频率会导致刀具的破损而降低刀具寿命,小的主偏角可降低刀具的疲劳磨损,因此在钛合金切削中应采用小的主偏角和小的振动频率。
上海交通大学 [102、103] 通过检测电枢电流的方式来实现切削力误差的补偿。该方法的特点是通过霍尔元件实时检测电动机电流,通过切削力和电流之间的关系模型间接得出切削力,通过位移传感器实时检测由切削力引起的位移误差,之后通过模糊神经网络建立机床切削用量、电动机电流和力误差的数学模型,通过FANUC数控系统的外部坐标偏移功能实现切削力误差的实时补偿,并在一台双主轴数控车床上实验成功。
另外,各国学者 [104~111] 还针对不同数控机床的切削力误差进行了研究,分别对车削、铣削等切削力及切削力引起的误差进行建模补偿并取得了一定成果。
随着误差补偿技术的日益完善,各种发明专利不断出现。Hermle Harald发明的关于机床热膨胀补偿装置获得了德国专利,该装置可以迅速而精确地补偿机床机构在工作过程中的线性热膨胀,在机床起动后加热期具有特效。H. Youden David [112] 发明的装置获得了美国专利,该装置可连续测量精密车床的热变形,并将这些变形信息传递给机床数控系统,以便在控制机床工作机构移动过程中予以补偿。Schmid Robert [113] 关于机床热变形的补偿系统获得了德国专利,提出的补偿方法适用于CNC加工中心。
在国内,上海交通大学、西安交通大学、天津大学、华中科技大学、大连理工大学、哈尔滨工业大学、同济大学、华侨大学、广西大学、沈阳工学院、沈阳机床(集团)有限责任公司、上海机床厂有限公司、济南第一机床厂、沈机集团昆明机床股份有限公司等都对机床误差补偿技术进行了研究,并取得了大量成果 [117~134] 。
1.3.2 数控机床误差补偿技术研究的现状
纵观国内外,在有关人员的不懈努力下,数控机床误差补偿技术有了较快的发展。但从目前来看,在国外,数控机床误差实时补偿技术大批量的在工业中应用的例子并不多,还没达到成熟的商业化程度;在国内,误差实时补偿技术大部分还停留在实验室范围,还未见在生产厂家批量数控机床上应用误差实时补偿技术的报道。这说明误差补偿理论和技术还有很大的余地可开发。目前,数控机床误差补偿技术的主要不足和难点如下:
1. 误差补偿运动控制的实现
误差补偿是通过移动(对于四轴以上还需转动)机床的运动副以使刀具或工件在机床空间误差的逆方向上产生相对运动而实现。误差补偿运动控制的实现除了要满足补偿精度外,还要满足实际应用的方便性和经济性,同时考虑到机床的动态误差及补偿的实时性。所以,对误差补偿运动控制实现的要求是精确性、实时性、经济性和方便性。从目前来看,补偿运动控制的实现可通过:
1)修改G代码补偿法 [131~133] ,其不足是实时性差。
2)压电陶瓷制动补偿法 [134] ,其不足是反应慢、刚度低。
3)开放式数控系统补偿法,其不足是绝大多数数控系统还未到开放程度。
4)数控系统内部参数调整补偿法,如螺距补偿、齿隙补偿、刀补等,其不足是仅静态补偿。
5)原点偏移补偿法 [135] ,其不足是受限于数控系统。
2. 数控机床误差的综合建模和补偿问题
目前,绝大多数的补偿将几何误差和热误差分开补偿,由于机床误差的复杂性,如定位误差等实质上既是几何误差(与机床坐标位置有关)又是热误差(与机床温度有关)。一般将这些误差作为几何误差进行补偿。但实际上,这些误差在不同的温度下是变化的,故对这种既是几何误差又是热误差的复合误差(严格说机床上的误差都与温度和力有关)要进行几何误差、热误差和力误差的综合建模和补偿。
3. 机床误差检测和辨识时间过长问题
由于机床误差特别是热误差取决于诸如室温、机床工况(主轴转速和进给速度等)、切削参数、切削液、加工周期等多种因素,而且机床热误差呈现非线性及交互作用,因此,这种检测和辨识通常需要很长时间。另外,由于机床上的误差元素众多,一般的激光测量仪测量,一次调整仅测得一项误差元素,如何高效快速地测量,也是个必须解决的问题。
4. 误差补偿模型的鲁棒性
在一个季节训练所得的误差补偿模型能否用于另一个季节,这是一个需要考虑的实际问题。这里,我们考虑的不是恒温的实验室而是工厂的大车间,环境温度对机床本身温度场有着一定的影响。据我们所做的补偿工作表明:用目前使用的建模方法得出的热误差补偿模型随着季节的变化难以保持长期非常正确地预测热误差。另外,就是相同类型、相同规格、相同使用时间、相同环境、相同切削条件的各机床,甚至同一机床不同时间获得的数据,得出的热误差模型之间也有差别,甚至差别很大,一般难以互相替代。从而造成在同型号批量机床补偿中,模型众多,使得建模时间太长且管理难度大。那么,能否创立一些出乎传统和常规的全新建模方法,使得其建立出来的误差补偿模型能长期(经历一年四季各温度阶段)非常正确有效地预测和补偿机床误差?另外,一个误差数学模型能否在多台同型号机床补偿中使用?由此对误差补偿模型的鲁棒性提出了更高的要求。
5. 五轴数控机床多误差实时补偿问题
目前国内外五轴数控机床补偿主要局限于几何误差建模及补偿,而且在理论上讨论的比较多,真正实际的动态实时补偿的实施和应用的实例还是不多。而随着五轴数控机床的普遍使用,为获得更好的加工精度或补偿效果,五轴机床的多误差动态实时补偿及其应用必不可少。
1.3.3 数控机床误差补偿技术研究的发展趋势
在国内外有关学者的不懈努力下,误差补偿技术已有了很大的发展,在各方面的应用越来越广泛。但是,由于机床各种误差有着复杂多变的特性,误差的产生是一动态过程,具有分布参数非线性、时滞的特点,它的大小从统计角度分析,其分布是非正态和不平稳的;误差也往往不是孤立出现的,而是伴随着热、力等众多因素;误差还具有多维坐标耦合效应,一个方向发生变化后,其他方向将受到关联,这也给补偿带来了困难。从另外一个角度看,误差补偿技术涉及面较广,包括数控技术、检测技术、传感技术、信号处理技术、微电子技术、材料技术、计算机技术、控制技术等。所以误差补偿技术还不很成熟,有很多问题待解决,很多理论待完善,很多技术待提高。从目前的发展状况及数控机床误差补偿的要求来看,数控机床误差检测与补偿技术的发展趋势主要为:
1. 多误差高效检测方法
数控机床、加工中心空间误差的快速检测是20多年来此领域的一个重要研究问题,也是一个未能很好解决的测量问题。众所周知,高速高精度下数控机床的(复杂)运动轨迹误差直接影响着被加工对象的几何精度,能否确切地掌握该误差,是进行在线补偿加工的必需。现有关于数控机床误差测量的传统方法主要包括基于直线运动轨迹的激光干涉仪和基于圆运动轨迹的球杆仪(DBB)为代表的直接测量方法,和各种1D、2D及3D标准加工件作标准为代表的间接测量方法。现有方法存在安装调整困难、测量时间长或者测量辨识结果不唯一,难以溯因等种种困难,难以适应现场在线、高效高精度的快速测量需求,限制了数控机床误差精密检测和补偿的实际大规模应用。2008年CIRP国际生产工程学会(关于机床制造、精度检测、精密加工的最高国际学术会议)仍然将数控机床和坐标测量机的误差检测方法与补偿作为大会主题报告,提出在可预见的未来10年内数控机床多误差的高效检测方法仍然是重要的研究问题。目前该领域的前沿研究领域包括数控机床误差的组合轨迹测量方法的研究、5轴机床旋转轴几何误差的快速测量R-TEST装置的研究与发展。
同时,由于机床误差,特别是热误差取决于诸如室温、机床工况(主轴转速和进给速度等)、切削参数、切削液、加工周期等多种因素,以及机床热误差呈现非线性及交互作用,导致数控机床热误差的检测和辨识通常需要很长时间。因此,机床热误差的高效鲁棒建模与辨识,建立一个能够适合不同机床、不同切削条件、不同季节,相对稳定的鲁棒性强的误差补偿模型,也是未来关于机床误差检测方面的重要研究课题。
2. 多误差的综合补偿
现有的误差补偿技术中,往往都是针对数控机床的某项或某几项误差元素,诸如研究较为广泛的几何误差、热误差等,而数控加工精度的影响因素众多,单靠某几项误差补偿难以有效消除数控加工过程中产生的众多误差,此外,数控机床的许多误差元素相互耦合、相互影响,单一的误差补偿可能会造成过补偿问题。因此,在机床几何误差和热误差补偿的同时,还必须考虑切削力和刀具磨损等引起的误差,并且建立各误差之间的耦合关系。在补偿研究中,目前大部分还没有考虑到切削力及刀具磨损所引起的误差。一般都假定,在传统的精加工中,切削力很小所导致的变形可以忽略。然而,随着强力切削应用的增长或在一些难加工材料切削中,切削力及刀具磨损误差变得重要起来。故很有必要进行机床几何误差、热误差、切削力误差、刀具磨损误差的综合补偿。这里的主要问题是如何建立包括机床几何误差、热误差、刀具磨损误差、切削力误差等分别属于静态误差(几何误差)、准静态误差(热误差、刀具磨损误差)、动态误差(切削力误差)等不同性质误差的综合数学模型,并能实现上述误差的解耦补偿。
3. 多轴误差的实时补偿
现有的建模手段多采用离线建模的方法,无论是神经网络理论还是各种先进算法都是采用离线训练的方法来获得误差模型,然后根据误差模型进行误差补偿,这种补偿方式属于静态补偿,对于加工过程中随机出现的误差无法感知和预测,更无从谈起补偿,因此需要开发一种能在线实时建模的误差补偿系统,这种系统高于专家系统,可实时辨识误差并根据需求建立动态的误差模型。与此同时,目前的研究与实践比较多的集中在三轴数控机床上,而随着五轴数控机床的普遍使用,为获得更好的加工精度或补偿效果,多轴机床,特别是带有回转工作台的五轴数控机床,其动态实时补偿及其实施和应用是必不可少的。
4. 实时补偿控制系统的网络化、群控化
随着制造业规模的不断扩大,企业对数控机床的拥有数量也不断增加,而传统的误差补偿只能采用单机版的方式,无法通过上一层的操作平台对多台数控机床的补偿实时信息进行监控和调整。而且,传统的补偿建模方法必须相关技术人员现场实际测试并建模后,将模型导入相关的补偿系统硬件中才能完成,这样就使得误差模型的建模工作只能由专业人员在工业现场来完成,既不经济,效率也低。因此,通过互联网络实现远程数控机床误差建模、模型下载以及模型调整,增强误差补偿技术的灵活性是未来一段时间内数控机床误差补偿系统的发展方向之一。
5. 补偿智能化与开放化
随着智能技术的日益成熟,数控机床将向智能型方向发展,而误差补偿技术也将会融入智能化的轨道。目前的数控系统是指令式数控系统,随着智能技术的发展,智能型数控系统将会在不久的将来诞生,而这种智能型数控系统本身将会集成误差补偿系统,这种智能的误差补偿系统会根据各误差元素对总误差的贡献以及总误差对加工精度的影响智能取舍,有时甚至会制造一些误差去抵消当前成为问题而又无法辨识的误差因素。因此,智能化误差补偿将是数控机床误差补偿技术发展的宏观趋势。与此同时,随着将来的纳米甚至更精密的数控加工中,数控机床的加工精度将会部分或全部依赖于误差补偿技术,误差补偿系统需要与各种数控系统实时交互,达到底层程序互容共享的目的,这同时也要求开放的数控系统,整个误差补偿系统与原有的数控系统均需要具有开放的控制接口,打破现有数控系统的封闭、独立和垄断。
近年来随着大数据和人工智能的发展,误差建模与补偿研究出现一些新趋势,需要结合深度学习等新兴机器学习方法,研究基于制造大数据的产线加工精度与制造大数据的关联关系,形成产线加工加工精度建模、预测与智能补偿的系统化解决方案,以满足国内制造企业对智能产线的迫切需求。
著者在教育部、04专项、国家重点研发计划和自然科学基金等项目的支持下,经过十余年专心致志、持续不断地对数控机床误差补偿技术的研究,取得了系统性的研究成果,在数控机床误差统一模型、复杂生热机理及热误差建模、旋转轴误差同时测量及解耦补偿等方面取得了理论创新,在数控机床智能实时误差补偿控制器方面取得技术突破,建立了数控机床误差测量、分析与补偿的技术体系。成果广泛应用于三~五轴各类机床,在数控机床装备行业、航空航天、汽车,以及3C的消费类电子等各类数控机床应用行业40多家企业1000多台机床上得到批量应用。具体主要成果如下:
1)提出了数控机床综合误差数学模型的建立方法,并提出了三轴数控机床全部4种结构的统一综合误差数学模型,以正确描述位置误差在机床三维运动空间中的分布,并将不同结构数控机床误差数学模型统一在同一个数学模型中。
2)提出了温度测点在机床上的优化布置方法和在众多温度元素中选择关键温度元素的方法,使得数控机床热误差(或主轴热漂移误差)数学模型的精确度更高、鲁棒性更好,而且热误差数学模型中的温度元素更少。
3)提出了机床主轴热漂移误差的多种建模方法,并提出了既是几何误差(与机床运动位置坐标有关)又是热误差(与机床温度有关)的复合误差的建模方法。
4)提出了五轴数控机床误差实时补偿策略,并建立了五轴数控机床误差补偿数学模型。
5)开发了数控机床误差实时补偿控制系统,高效、精确、经济、方便地实现了多误差(几何误差、热误差、力误差等)实时补偿,大幅度提高了机床加工精度。
6)开发了适用于国产数控系统的实时误差补偿功能模块,使得实时补偿在国产数控系统的机床上也可实施和应用。
7)将实时补偿技术实施和应用于多家企业的批量数控机床,提高机床精度50%~90%。


