2.1 等离子体的基本概念
2.1.1 等离子体的定义
等离子体是由大量带电及中性粒子集合组成的宏观体系 [1] 。它有两个显著特点:宏观上呈现准中性,正负离子的数量大致相等;集体运动效应。
等离子体由正离子、负离子、电子和不带电的中性粒子组成,不同带电及中性粒子之间是相互独立的。等离子体各带电粒子之间通过电磁力相互作用,这种作用力能使远距离的带电粒子产生耦合。这些粒子之间存在的多体自洽的结果使得粒子的运动表现为集体的运动,存在集体运动是等离子体的重要特征之一 [2-3] 。
等离子体态常被称为“物质的第四态”,与固态、液态、气态一样,是物质的一种聚集状态。物质的四种状态如图2.1所示。等离子体态形成的原因是中性气体中发生了一定程度的电离反应,产生了一定数量的带电粒子。当气体温度升高时,粒子之间的热运动动能将逐步达到气体的电离能,此时电离的过程可以通过粒子之间的碰撞发生 [1] 。
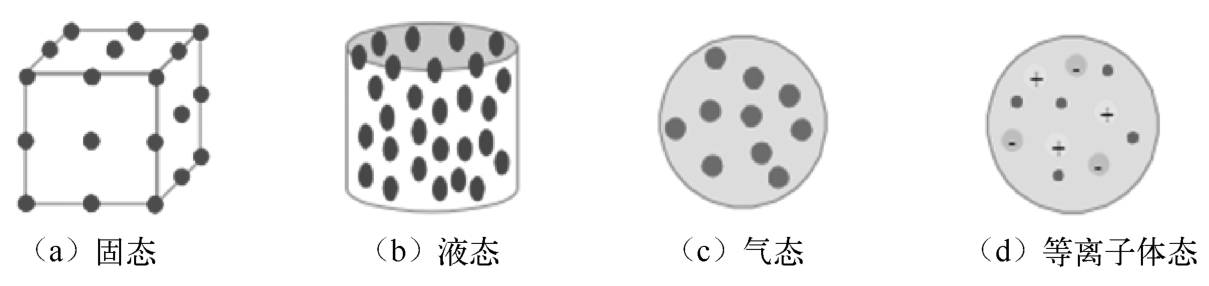
图2.1 物质的四种状态
通过加热的方式,物质四种状态之间可以产生转变,称为相变。我们不妨以水为例来进行说明。在1atm下,体系温度低至0℃以下时,水的微观基本组元(分子)的热运动动能小于分子之间的相互作用势能,因此相互束缚,在空间的相对位置固定,水凝结成冰,这就是固体状态。当体系的温度升高至0℃以上时,冰融化成水,分子间的热运动动能与分子之间的相互作用势能相当,分子可以在体系内部自由地移动,但在边界面上,由于表面束缚能的存在,大多数分子无法克服这种表面束缚,会存在一个明显的表面,这就是液体状态。当体系的温度高至100℃以上,水气化为水蒸气,此时分子之间的热运动动能可以克服分子之间的相互作用势垒以及表面束缚能,因此分子变成彼此自由的个体,这就是气体状态。当体系温度继续升高时,分子间的热运动动能足以克服分子键能的时候,即分解成原子,体系的基本微观组元由分子变成原子,但物态并没有发生本质的变化,仍是气体状态。然而,当温度进一步增高,使得原子(分子)间的热运动动能与电离能基本相当时,就会发生电离过程,从而变成了含有电子、正离子、负离子和中性粒子的电离气体。这时长程的电磁力会起作用,使体系出现全新的运动特征,这就是等离子体态 [2] 。
等离子体并不都是完全电离的气体,但只有达到一定电离度的电离气体才具有等离子体的特性。简单地说,当某一体系中“电性”比“中性”更重要时,便可称为等离子体。由于热平衡麦克斯韦(Maxwell)分布的高能尾部粒子的贡献,处于热力学平衡态的气体总会产生一定程度的电离,其电离度由沙哈(Saha)方程给出 [4] 。
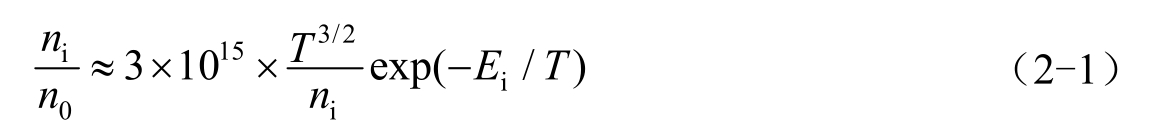
式中, n i 为离子密度; n 0 为原子密度; T 为温度; E i 为电离能。除非特别说明,一律采用国际单位制,但温度与能量一样,以电子伏特(eV)作单位。电子伏特与开尔文(K)的换算关系为 [4]

2.1.2 等离子体的参数空间
宇宙中绝大多数物质处于等离子体态。地球上天然的等离子体,如闪电、极光等,存在于远离人群的地方。从地球表面向外,大气外侧的电离层、日地空间的太阳风、太阳日冕、太阳内部、星际空间、星云及星团,毫无例外都是等离子体 [5] 。
此外,人造的等离子体也越来越多地出现在我们生活中,如日光灯中用于发光的电离气体。等离子体刻蚀、镀膜、表面改性、喷涂、烧结、冶炼、加热、有害物处理是等离子体几种典型的工业应用 [4] 。
与另外三种物态相比,等离子体的参数空间非常宽广。以描述物态的两个基本热力学参数密度和温度而言,等离子体的密度为10 3 ~10 33 m -3 ,跨越了30个量级,温度为10 2 ~10 9 K,跨越了7个量级,如图2.2所示。
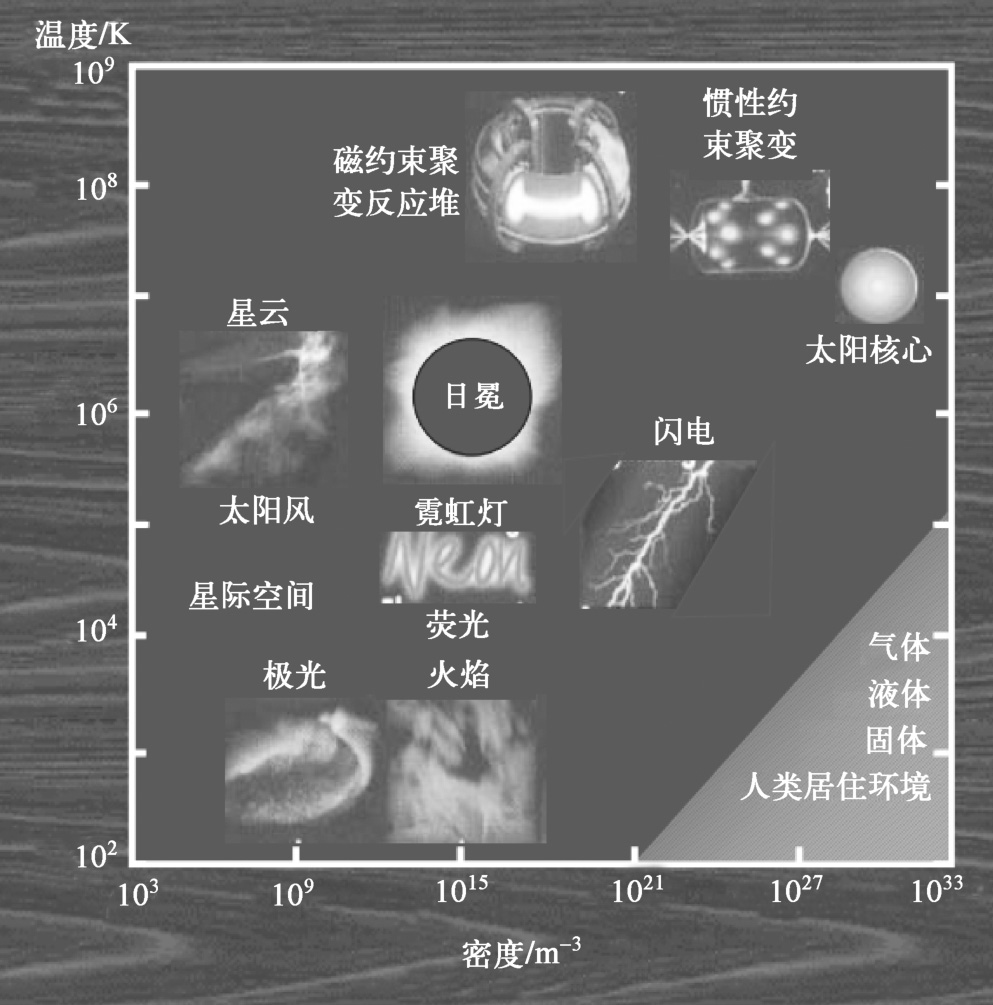
图2.2 等离子体的参数空间
2.1.3 等离子体的描述方法
尽管等离子体的参数范围十分巨大,但其描述的方法却基本上是一致的。多数情况下,等离子体是一个经典的、非相对论的体系。其绝大多数行为效应可以用经典的电动力学理论来描述和解释。量子效应只有在粒子之间间距与粒子德布罗意波长相当时才显示出来,这对应着温度极低(10 -2 eV)、密度达到固体密度(10 27 m -3 )的情况。只有在相对论粒子的等离子体(如大功率微波器件或自由电子激光中的相对论电子束)中,才需要考虑相对论效应 [6] 。
等离子体的描述可以分为电磁场和粒子体系两个部分。一般来说,用麦克斯韦方程组来描述电磁场的行为,而用统计力学和流体力学来描述粒子体系的行为。
在统计力学的框架下,等离子体的行为可由粒子速度概率分布函数描述,如玻尔兹曼(Boltzmann)方程 [7] 。在该体系下,对等离子体的描述依赖于统计物理,并利用守恒定律确定粒子分布函数的演化行为。对统计描述的方法做相应近似,通过速度分布函数对速度积分,就可以得到粒子速度、密度等宏观参数,即流体力学描述,此时等离子体被视为一种电磁相互作用起主导的流体。等离子体作为流体的动力学变量有密度、温度(能量)和速度,可用动量守恒方程、连续性方程和能量守恒方程耦合电磁场求解。
2.1.4 等离子体的关键特征和参量
1.德拜屏蔽和等离子体的空间尺度
等离子体由“自由”的带电粒子组成,与金属对静电场的屏蔽类似,任何试图在等离子体中建立电场的行为,都会受到等离子体的阻止,这就是等离子体的德拜(Debye)屏蔽效应。相应的屏蔽层称为等离子体鞘层 [8] 。
假设在等离子体中插入一电极,这一行为将试图在等离子体中建立电场。在这样的电场作用下,等离子体中的电子将向电极处移动,而离子则被排斥。这导致由电极所引入的电场仅局限在较小尺度的鞘层中,如图2.3所示。
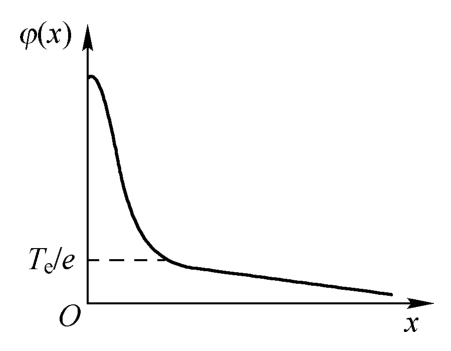
图2.3 等离子体鞘层电势分布( T e 为电子温度, e 为电子电荷量, x 为粒子空间位置, φ 为鞘层内电势分布)
若等离子体的温度为0K,则大量的电子可以接近于电极(设电极表面敷以介质,表面不收集电流,也不产生复合),屏蔽层的厚度将趋于零,电场则完全被屏蔽。若等离子体的温度不为0K,则屏蔽后的电势满足 eφ / T e ≈1时,电子可以挣脱此势阱并逃逸出,因此电势没有完全被屏蔽掉,有 T e / e 量级的电势将延伸进入等离子体中,屏蔽层的厚度也有限。可以简单分析这种静态的德拜屏蔽过程。静电势 φ 满足泊松(Poisson)方程 [5] :

式中, ε 0 为真空介电常数; n i 为离子密度; n e 为电子密度。因此,在热平衡状态下,它们满足玻尔兹曼分布:
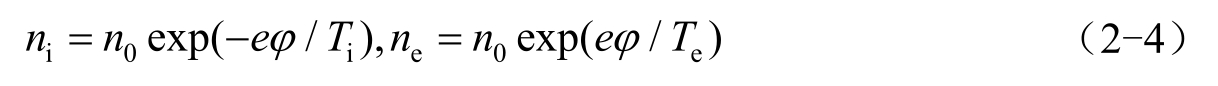
式中,
T
i
为离子温度;
T
e
为电子温度;
n
0
为远离扰动电场处(电势为零)的等离子体密度(电子密度与离子密度相等)。将式(2-4)代入泊松方程,即电势方程,该方程为典型的非线性方程,无解析解。由式(2-4)可以看出,当
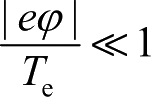 时,
n
e
≫
n
0
,电子被捕获并大量积累,离子则被排出,大部分的电势被这些电子产生的电场屏蔽。若不考虑接近电极处电势较大的区域,只看电势满足
时,
n
e
≫
n
0
,电子被捕获并大量积累,离子则被排出,大部分的电势被这些电子产生的电场屏蔽。若不考虑接近电极处电势较大的区域,只看电势满足
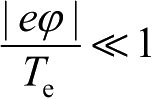 的空间,则可以将玻尔兹曼分布作泰勒级数展开,并取线性项,则有
[4]
的空间,则可以将玻尔兹曼分布作泰勒级数展开,并取线性项,则有
[4]

这里,定义电子、离子的德拜长度分别为 λ De 、 λ Di ,等离子体的德拜长度为 λ D 。
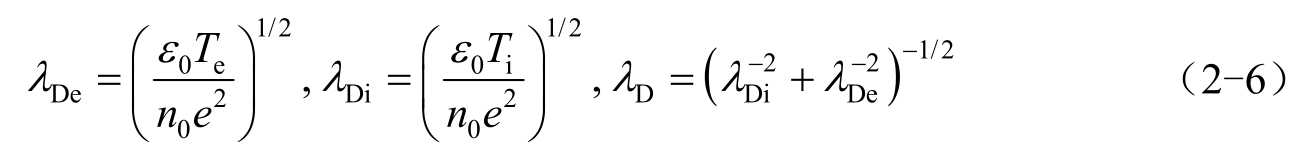
在一维情况下,式(2-5)的解为

式中, φ 0 为 x =0处的空间电势; x 为一维空间中粒子的位置。
电势以指数衰减的形式渗透在等离子体中,德拜长度 [4] 定义为等离子体屏蔽外电场的空间尺度,即为式(2-6)。
静态等离子体的德拜长度取决于低温成分的德拜长度。在电子运动较快的过程中,离子无法响应电子的变化,在鞘层内不能随时达到热平衡的玻尔兹曼分布,只起到常数本底作用,此时等离子体的德拜长度只由电子成分决定 [3] 。
在等离子体中,每一个离子或电子都具有静电库仑势,会受到邻近其他离子与电子的屏蔽,则屏蔽后的库仑势为 [4]

式中, q 为带电粒子的电量; r 为粒子的位置半径。
这种屏蔽的库仑势使带电粒子对周围其他粒子的影响是有限的,仅局限于以德拜长度为半径的德拜球内。等离子体系统的基本长度单位是德拜长度,可以认为,等离子体由许多德拜球组成。在德拜长度内,粒子可以清晰地感受到周围粒子的存在,存在着以库仑碰撞为特征的两体相互作用;在德拜长度外,由于其他带电粒子的干扰和屏蔽,直接的粒子两体之间相互作用消失,而是由大量粒子共同参与的集体相互作用。换句话说,在等离子体中,带电粒子之间的长程库仑相互作用可以分解成两个不同的部分,一部分是在德拜长度以内的以两体为主的相互作用,一部分是在德拜长度以外的以集体为主的相互作用。等离子体作为第四物态的最主要原因是其集体相互作用性质 [2] 。
2.等离子体的特征响应时间
等离子体的时间响应尺度是等离子体的另一个重要特征参数。我们已经知道,等离子体可以将任何空间的(电)干扰局限在德拜长度量级的鞘层之中。但是,建立这种屏蔽需要一定的时间。若将电子以平均热速度跨越鞘层空间所需要的时间作为建立一个稳定鞘层的时间尺度,这就是等离子体对外加扰动的特征响应时间 [9] :

式中, m e 为电子质量; n 0 为电子密度。
用这种方法估算的等离子体响应时间与等离子体集体运动的特征频率相关。如图2.4所示,假设等离子体在某一处( x =0),电子相对离子有一个整体的位移( x >0),则在 x =0处将形成电场,这使得电子受到指向 x =0处的静电力,电子将向 x =0运动。由于惯性作用,电子将冲至 x <0处,如此电子将产生围绕平衡位置 x =0处的振荡。电子运动方程为 [5]
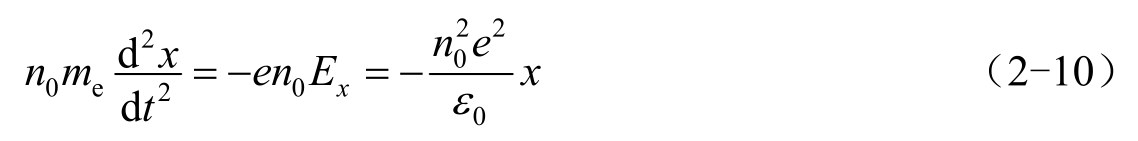
式中, E x 为 x 方向上的电场强度。式(2-10)的解为简谐振荡,称为朗谬尔(Langmuir)振荡或电子等离子体振荡,振荡频率为

ω pe 称为(电子)等离子体频率,显然其与等离子体响应时间互为倒数。
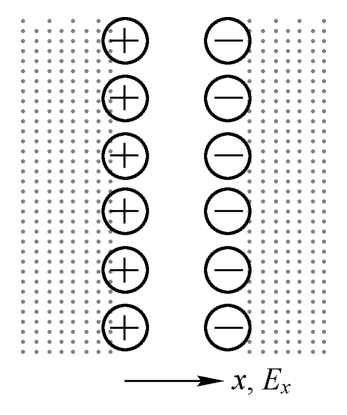
图2.4 等离子体振荡示意图
2.1.5 等离子体判据
等离子体作为物质的一种聚集状态,必须要求其空间尺度远大于德拜长度,时间尺度远大于等离子体响应时间。在这种情况下,等离子体的集体相互作用起主要作用,在较大的尺度上正负电荷数量大致相当,所谓的准中性条件成立。
等离子体判定的标准曾为准中性条件,正负离子相等的带电粒子系统是中文“等离子体”的含义。但实际上,即使准中性条件不成立,只要系统满足上述的时空要求,同样可以出现以集体相互作用为主的等离子体特征 [2] 。
对于有些电离气体,体系中不仅包含带电粒子,还有中性粒子。当带电粒子与中性粒子之间的相互作用强度远小于带电粒子之间的相互作用时,中性粒子的存在基本不影响带电粒子的运动行为,同完全电离气体组成的等离子体相近,因此这种部分电离的气体也属于等离子体 [2] 。
近距离碰撞是带电粒子与中性粒子之间相互作用的唯一形式。相互作用的强弱程度可以用碰撞频率 v en 来表示。带电粒子之间的相互作用可以分成两体的集体相互作用和库仑碰撞两部分,这两种作用的大小可以用库仑碰撞频率 v ee 和等离子体频率 ω p 来表征。因此,如果有

在这种情况下,可以忽略中性粒子的作用,体系处于等离子体态。我们可以用库仑碰撞频率来估计,由于带电粒子之间的库仑碰撞截面很大,在常规情况下,当电离度为0.1%时,便可以忽略中性粒子的作用。若电离度更小时,电离气体虽然具备一些等离子体的性质,但不能忽略中性粒子的影响。若中性粒子的碰撞频率远远大于库仑碰撞频率和等离子体频率时,等离子体特征消失,这种微弱电离的气体不能称为等离子体 [2] 。
德拜屏蔽是一个统计意义上的概念,暗示了在一个德拜球中应具有足够多的粒子。引入等离子体参数 [3] :

式中, T e 为电子温度; Λ 为以德拜长度为半径的德拜球体内的粒子数量,满足 Λ ≫1。
等离子体参数也衡量了粒子平均动能与粒子间平均势能之比。通常情况下等离子体参数是一个大量,等离子体中粒子的直接相互作用可以忽略。在极稠密的或温度极低的等离子体中,等离子体参数可以小于、甚至远小于1,这种等离子体称为强耦合等离子体,已经不是常规等离子体的范畴。稠密的强耦合等离子体的例子有惯性约束聚变的核心等离子体、白矮星天体等离子体、金属固体等离子体等。温度低的强耦合等离子体的典型例子是极低温度的非中性等离子体,因为在常规等离子体中较低的温度必然导致正负离子间的复合 [3] 。
等离子体概念可以推广,但核心内涵是集体行为起支配作用的宏观体系,分类如下。
(1)非中性等离子体:宏观上非电中性的体系,若由离子或电子单一电荷成分组成,则称为纯离子等离子体或纯电子等离子体。非中性等离子体存在着很强的自电(磁)场,自场对其平衡起重要作用 [4] 。
(2)固态等离子体:金属中的电子气、半导体中的自由电子与空穴在一定程度上具有等离子体特征。
(3)液态等离子体:电解液中的正负离子是自由的,具有等离子体特征。
(4)天体物理中的星体:如果将万有引力与库仑力等价,则在天体尺度中,由星体构成的体系可视为一种类等离子体。
(5)夸克-胶子等离子体:将强相互作用与电磁相互作用类比,某些概念可用于粒子物理领域。
2.1.6 等离子体鞘层
等离子体在半导体生产中的广泛应用有两个主要原因:一是离子的能量(电离能和动能)和化学活性远高于中性原子或分子的能量,因而在极高温条件下才能产生的化学反应能在等离子体中高效完成;二是带电离子可以在电场下加速而具有方向性,进而可进行方向性刻蚀或者沉积。离子在晶圆表面的方向性通常是通过控制等离子体鞘层电场来实现的。
1.概念
等离子体中明显呈电荷非中性的区域,称为等离子体鞘层。鞘层内部存在较强的电场,其作用范围约为德拜长度量级。在等离子体与固体各种接触面上通常存在鞘层;在等离子体内部密度或温度剧烈变化的地方,也可以存在鞘层 [2] 。
对于悬浮在等离子体中的金属电极(器壁)或绝缘体,由于电子运动速度一般大于离子运动速度,电子流较大,电子将在器壁积累形成电场,这个电场使得进入鞘层的电子流减小而离子流增大,最终两者相等。因而,在简单情况下,等离子体相对于绝缘器壁的电势要高约几倍的 T e / e 值,如图2.5(a)所示。在电极有电流的情况下,电极相对等离子体的电位可正可负。一般来说,当流向电极的电子流较大时,电极相对等离子体的电势为正值,如图2.5(b)所示;当流向电极的离子流较大时,电极相对于等离子体的电势为负值,如图2.5(c)所示 [3] 。
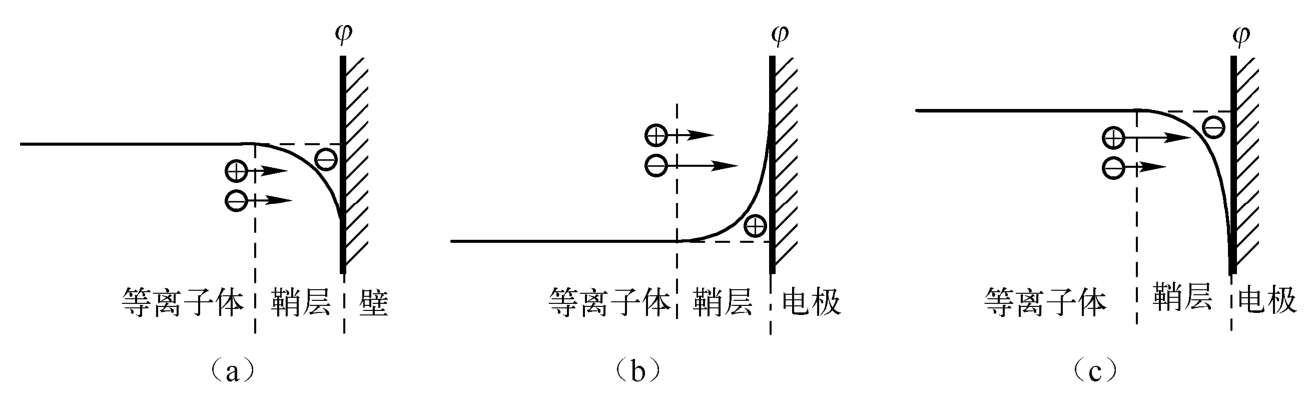
图2.5 等离子体鞘层及鞘层电势分布
2.稳定鞘层判据
让我们考察一维鞘层的电势分布,参考图2.5(c), x 轴方向由等离子体指向器壁。不考虑离子的温度,设离子在进入鞘层之前具有定向速度 u 0 ,则由能量守恒关系,鞘层中离子的速度为

式中, m i 为离子质量; φ 为鞘层内空间电势。
离子密度的空间分布直接由离子的连续性方程给出。
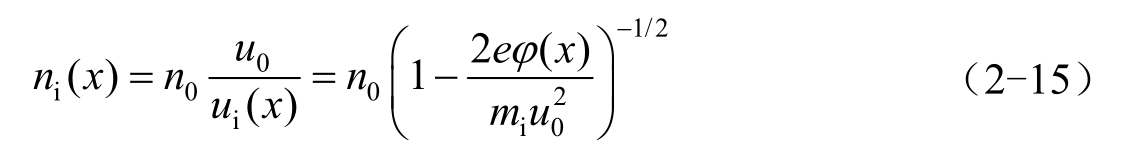
式中, n 0 为鞘层外等离子体的密度。电子密度满足玻尔兹曼分布。
应用泊松方程,就可以得到鞘层中电势所满足的方程:
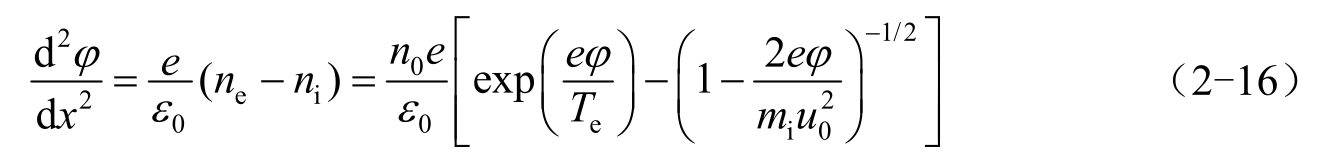
一般情况下,此方程只能依赖于数值求解,但如果我们考察电势绝对值较小的区域,则有
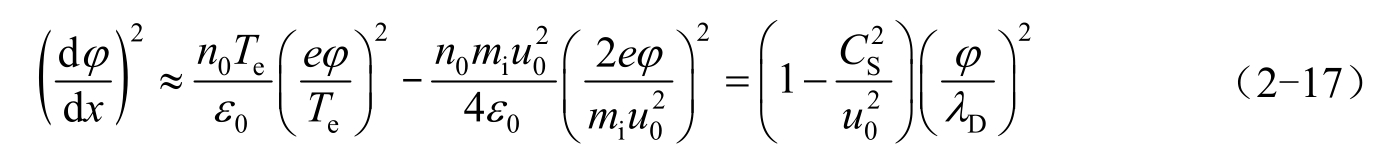
式中, C S 为鞘层电容。
很明显,式(2-17)有解的条件要求:

式中, M 为流体的定向速度与离子声速之比,称为马赫(Mach)数。这个条件是稳定鞘层存在的必要条件,称为玻姆(Bohm)鞘层判据。
稳定鞘层存在的要求是离子进入鞘层时的速度大于离子声速。通常这种定向的速度不是由外界施加的,而是等离子体内部电场空间分布自洽的调整结果。也就是说,自鞘边界向等离子体内部延伸,有一个电场强度较弱的被称为预鞘的区域(预鞘区)。在预鞘区,离子被缓慢加速直至离子声速。实际上,鞘层和预鞘区并没有严格的区别,通常将离子达到离子声速的位置确定为鞘层的边缘,同时认为在预鞘区,准中性条件仍然满足。


