2.4 逻辑三要素之推理

前面提到， 逻辑就是关系。所谓推理，就是研究语句、判断、命题之间相互关系的学问 。逻辑推理可以分为演绎推理（Deductive Inference）、归纳推理（Inductive Inference）和溯因推理（Abductive Inference）。

2.4.1 演绎推理：因为，因为，所以

演绎推理旨在阐明前提和结论之间的关系，为评估演绎论证是否有效提供方法。

演绎推理是一个从一般到特殊的过程。我们通常说的“大前提、小前提、结论”的三段论形式就是典型的演绎推理。

例如，“所有人都会死，苏格拉底是一个人，因此苏格拉底会死”。大前提是“所有人都会死”，小前提是“苏格拉底是一个人”，结论是“苏格拉底会死”。这是一种必然性推理（保真推理），因为其结论就包含在前提之中，“所有人会死”本身就包含“苏格拉底会死”。

演绎逻辑在历史上出现了两种杰出的理论。一种被称为“古典逻辑”或“亚里士多德逻辑”，开创这种理论的是古希腊哲学家亚里士多德，他关于推理的论述被收集成册，称为《工具论》；另一种被称为“现代逻辑”或“现代符号逻辑”，主要形成于20世纪。

古典逻辑和符号逻辑都是研究演绎推理的形式（form），所以也被称为形式逻辑。

也就是说，对于一个推理来说，首先要保证其在形式上是有效的。如果推理形式有效且前提为真，那么结论必定为真；如果形式是无效的，即使前提为真，结论也不一定为真。“真”和“假”的概念适用于命题，“有效性”和“无效性”适用于逻辑形式。

例如下面的论证：

虽然前提（premise）是真的，但是其论证形式是无效的（否定前件谬误，后续会介绍），所以其结论是无效的，同时也是假的。

1.古典逻辑

古典逻辑（亚里士多德逻辑）主要处理不同对象的类之间关系的论证 。类是指共有某种特定属性的对象的汇集。

类与类之间的3种关联方式如下。

（1）全包含（wholly included），例如狗的类和哺乳动物的类。

（2）部分包含（partially included），例如运动员的类和女人的类。

（3）互斥（exclude），例如三角形的类和圆形的类。

基于类和类之间的关系，有以下4种直言命题。

（1）全称肯定命题（A命题）：所有S是P。例如所有政客都是说谎者。

（2）全称否定命题（E命题）：没有S是P。例如没有政客是说谎者。

（3）特称肯定命题（I命题）：有S是P。例如有政客是说谎者。

（4）特称否定命题（O命题）：有S不是P。例如有政客不是说谎者。

基于这些命题，有多种组合形式。古典逻辑学家很细致地研究了这些形式，总结出三段论的15个有效形式。

例如下面的论证：

因为这个论证形式是EAE-1，而EAE-1是15个有效论证形式之一，所以这是一个有效论证。又因为其前提是真的，所以结论也是真的。

2.符号逻辑

所谓符号逻辑，就是利用符号来表示逻辑中的各种概念 。1847年，英国数学家布尔出版了著作《逻辑的数学分析》，建立了“布尔代数”，并创造了一套符号系统。布尔建立了一系列的运算法则，利用代数的方法研究逻辑问题，初步奠定了数理逻辑的基础。

目前，符号逻辑已经超出逻辑学的范畴，成为数学的一个分支，同时也是计算机科学的基础。

逻辑代数也叫作开关代数，它的基本运算是逻辑加、逻辑乘和逻辑非，也就是命题演算中的“或”“与”“非”。运算对象只有两个数0和1，相当于命题演算中的“真”和“假”。逻辑代数的运算特点如同电路分析中的开和关、高电位和低电位、导电和截止等现象一样，都只有两种不同的状态，因此它在电路分析中得到了广泛的应用。

利用符号化和公式化，我们可以对逻辑命题进行数学演算，比如符号～代表否定，因此p=q和p=～～q是等价的，即双重否定等于肯定。同样，我们在计算机中的逻辑运算（与、或、非）也是完全符合符号逻辑的。

再比如，如下的论证形式都是无效的，因为犯了肯定后件和否定前件的谬误。

这两个谬误很容易通过例子看出来，前面的“比尔·盖茨不是富有的”的例子就是一个典型的否定前件谬误；而如下的“华盛顿之死”的例子是肯定后件谬误。因此，所有否定前件或者肯定后件的论证形式，都是无效的。

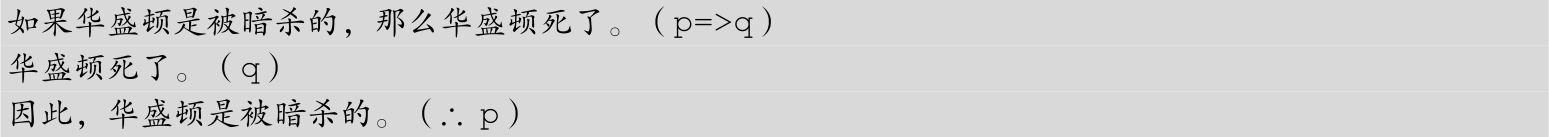
2.4.2 归纳推理：从特殊到一般

归纳推理是以一类事物中的若干个别对象的具体知识为前提，得出有关该类事物的普遍性知识的结论的过程。

例如：

这就是一个典型的归纳推理。然而，同样的推理用在下面的案例中就出现了问题，因为我们知道还有黑天鹅的存在。

这也是为什么有很多哲学家认为归纳法虽然可以得到新知识，但是因为不能穷举，所以永远也得不到真理。然而，演绎法虽然可以保真，但因为结论蕴含在大前提中，又不能产出新知识，因此如果最后推导出有真理存在，那么真理只能是先验的（先于我们的感觉经验，先天存在于我们的意识之中）。

然而科学知识都是来自科学归纳法的，所以真正的科学都是可以被证伪的，即当一种科学理论与最新的发现发生矛盾的时候，就需要一种新的理论来代替它。爱因斯坦的相对论虽然在牛顿力学的基础上迈出了一大步，但还是受到了量子力学的挑战，因此我们还需要一个能够解释所有力学现象的统一场论。这也是爱因斯坦终其一生都没有完成的工作，只能期待另一个“爱因斯坦”来完成了。

实际上，归纳和演绎并不是割裂的，而是彼此联系的，主要有以下两个原因。

（1）为了提高归纳推理的可靠程度，需要运用已有的理论知识对归纳推理的个别性前提进行分析，把握其中的因果性、必然性，这就要用到演绎推理。

（2）归纳推理依靠演绎推理来验证自己的结论。同样，演绎推理要以一般性知识为前提，这通常要依赖归纳推理来提供一般性知识。

这一点在软件工程的建模工作中得到了充分的体现， 建模是一个归纳工作，我们通过抽象问题域里具有共同特性的类来建立模型。为了验证模型的有效性，我们会使用演绎的方法去推演不同的业务场景，看看模型是否能满足业务的需要 。这样的工作往往不是一次成型的，而是交替往复，最终才能得到一个相对合理的模型。

2.4.3 溯因推理：大胆假设，小心求证

溯因推理就是我先知道了答案，再去追溯原因的推理。这种推理方法最早也是由亚里士多德提出的，他在著作《前分析篇》中提到了一种“还原推理模式”，说的正是溯因推理。

演绎推理的方法是由A推理出B，而溯因推理是在看到了B后，推理出导致B的最佳解释，可以理解为根据结果B去推测原因A的推理方法。换句话说，溯因推理是解释已知事物的过程。

如何进行溯因推理呢？ 简单来说，就是8个字：大胆假设、小心求证。

假如你家卫生间的地上出现了一滩积水，需要你去推理一下它的成因，你该怎么办？

按照这8个字，你首先要做的是“大胆假设”。能够造成卫生间地上有积水的原因比较多，比如卫生间的屋顶漏水、抽水马桶漏水，或者有人在地上放了冰块。

接下来，要从众多可能原因中找到一个最贴近现实的假设。因为屋顶漏水和地上有冰块都难以解释水是在抽水马桶一侧的现象，而且冰块也不大可能出现在卫生间。综合考虑这些因素后，你就能得出一个最贴近现实的假设，那就是抽水马桶漏水。

那么，怎样才能知道卫生间的积水是来自抽水马桶漏水呢？这就需要对这个假设进行验证了，也就是“小心求证”。这里的验证并不困难，你只需要擦干地上的水，看是不是有水从马桶里漏出来，即可验证假设是否正确。

做科学研究，也离不开大胆假设、小心求证。

1845年，科学家发现天王星的运动数据和其他行星比起来出现了2分钟的弧度差值。勒维耶提出一个假设：天王星的差值是由另一颗（未发现的）行星引起的，基于这样的假设，那颗新行星——海王星很快被发现。

对于程序员来说，基本每天都在运用这种溯因推理。我们通常说的故障排查（Trouble Shooting）就是溯因推理，用的手段基本上也是假设和求证。

比如，我们收到系统异常报警后去查看系统日志，发现是一个依赖服务报了超时（Timeout）错误。我们的第一反应是：是不是网络出现了问题（假设）？接下来开始ping依赖服务的IP，发现网络没问题（求证）。于是我们提出了新的假设：是不是依赖服务内部出现了什么问题？接下来开始排查依赖服务的日志，发现是因为一个数据库操作过于频繁，导致响应时间超时。可是这部分的代码很长时间没有修改了，为什么偏偏今天出现问题呢？通过进一步排查，我们发现是缓存服务器出现了问题，导致本来调用缓存的操作全部被打到了数据库上。那么为什么缓存服务器会宕机呢？通过进一步追查，发现是最近使用缓存的人比较多，内存空间不足导致了宕机。至此，我们才算真正找到了问题的根因（Root Cause）。