3.4 金字塔中的逻辑
第2章中提到, 逻辑就是关系 。这个关系可以是演绎关系、归纳关系、因果关系、时间关系、空间关系、程度关系、并列关系、类比关系,等等。 所谓的“有逻辑”,是指这个关系是合理的,道理是通顺的 。
逻辑是我们构建结构的基础,在结构中起着至关重要的作用。好的结构离不开清晰、有效、正确的逻辑,只有厘清逻辑关系,才能构建出好的结构,否则即使你搭建了结构,依然逃不脱那一片混沌。
在金字塔结构中,总体上有两个方向的逻辑关系,即纵向逻辑关系和横向逻辑关系。如图3-5所示,一个好的金字塔结构,需要 在纵向关系上满足结论先行、以上统下;在横向关系上,满足归类分组、逻辑递进 这4个基本原则。用一句话概括,就是“论证类比”。
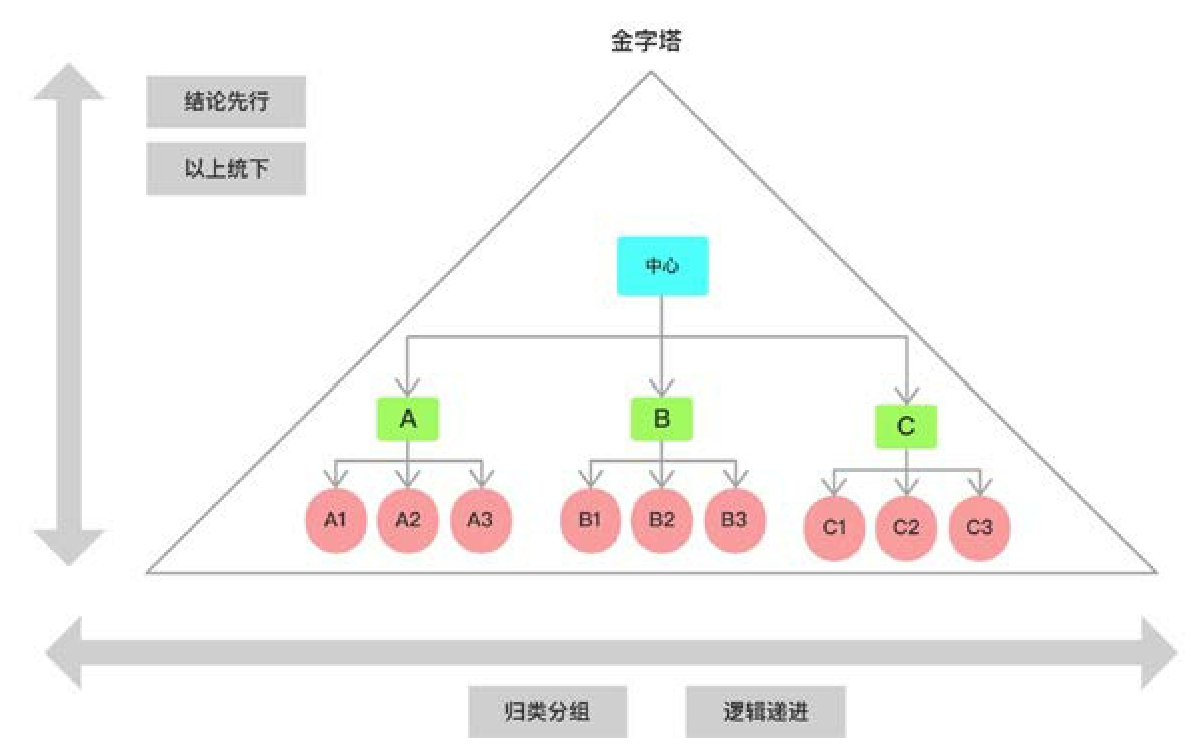
图3-5 金字塔结构的基本原则
(1)纵向关系:纵向是层次关系,上一层思想是对其下一层思想的概括,下一层是对上一层的解释和支持。
● 结论先行(“论”):所谓结论先行,就是要先抛结论。这一点在与人沟通的时候尤其重要,就像很多人铺垫了半天,也不说结论。写代码也一样,主方法是中心论点,子方法是对主方法的结构化分解。
● 以上统下(“证”):金字塔是一种层次结构,上一层是对下一层的统领和抽象,比如水果是对苹果、橘子的抽象,所以在上一层。
(2)横向关系:横向是关联关系,每组中的思想必须属于同一逻辑范畴,并按照逻辑顺序组织。
● 归类分组(“类”):将内容相似的思想归为一类,为进一步归纳抽象做好准备。
● 逻辑递进(“比”):分组中的思想需要有逻辑递进关系,即它们必须属于同一个逻辑范畴,且满足一定的逻辑顺序。
3.4.1 纵向逻辑关系
在纵向逻辑关系上,主要运用的是演绎逻辑和归纳逻辑。如果你还不清楚这两种逻辑,也可以回看第2章的内容。
1.演绎逻辑
演绎是一种线性的推理方式,最终是为了得出一个由逻辑关系词“因此”引出的结论。在金字塔结构中,位于演绎论证过程上一层的思想是对演绎过程的概括,重点是在演绎推理过程的最后一步,即“因此”引出的结论。比如图3-6所示的演绎逻辑示例。

图3-6 演绎逻辑示例
“甲公司值得收购”是这个演绎推理的结论,遵循结论先行的原则,在表述时我们应该先抛结论。试想,你在汇报工作的时候说“甲公司是一家非常不错的公司,它在A方面有这样的表现……,在B方面是行业里的前几名……”你这样滔滔不绝地讲10分钟,别人仍然不知道你说甲公司好的目的是什么。所以更好的做法是结论先行——“甲公司值得收购,因为第一……,第二……,第三……”
麦肯锡有一个“电梯原则”,即要求你在极短的时间(坐电梯的时间)内把一件事情说清楚,这需要你不仅有很强的整合能力,还要有“结论先行”的结构化思维,否则很难把事情说清楚。
按照金字塔原理的结构组织方式——上一层的思想是对演绎过程的概括,我们可以得到如图3-7所示的结构。
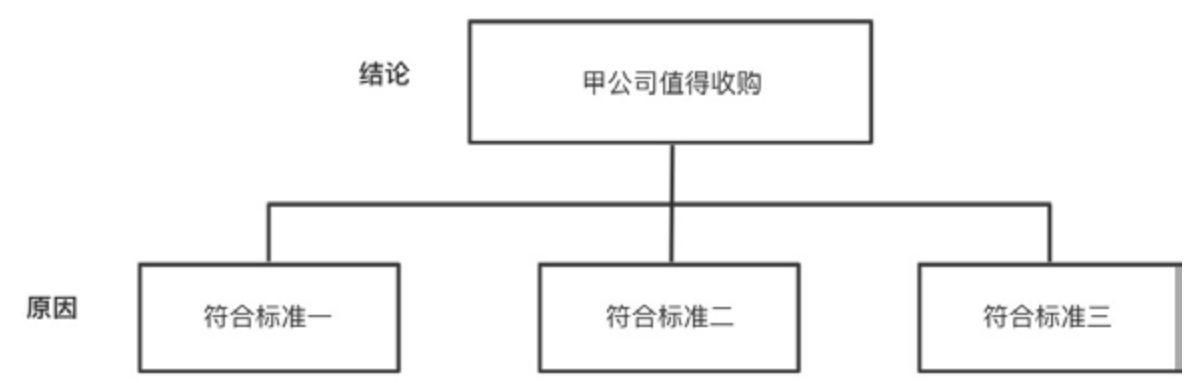
图3-7 结论先行的结构
需要注意的是,在表述中,大前提有时会被省略或变成默认假设。比如对于上述示例,我们通常会省略大前提,直接说“甲公司符合这3项标准,因此甲公司值得收购”,这是我们平时在做逻辑判断时特别需要注意的。在2.6.2节的错误假设中提到,很多的默认假设不一定是正确的,这种情况下的假设是不能忽略的。
2.归纳逻辑
归纳逻辑比演绎逻辑要难,因为归纳需要我们有更强的抽象能力,由抽象出的新概念去统领其下的子概念。在归纳的时候,我们大脑要发现事物(思想、事件、事实)中具有的共性和共同点,然后将其归类到同一个组中,并说明其共性。归纳逻辑不是线性的,它需要在已有信息的基础上提升一个抽象层次,得到新概念。
比如,苹果和橘子的上一个抽象层次是“水果”,这种抽象层次的提升可以让水果在纵向关系上统领苹果和橘子。“水果”这个新概念的抽象需要我们具备相关的知识背景。一个4岁的小孩可能还不知道水果的概念,就不能做出这样的抽象。另外,抽象有时还需要创造性和想象力,比如我问你“金鱼和激光笔有什么共性?”,你可能会觉得有点莫名其妙,这是一个脑筋急转弯,答案是“它们都不会吹口哨”,这样的答案需要我们有一定的想象力和幽默感。
虽然归纳逻辑比演绎逻辑要难,但是作为人类最重要的两种逻辑思维之一,归纳是我们发现新知识的唯一途径,也是科学研究的基础。它能帮助我们发现隐藏在信息中的因果关系,对于那些具有普遍效应的因果关系,我们可以将其提升为“理论”和“定律”。比如,牛顿通过观察苹果的下落,发现了地球上所有的物体都受到地球的“吸引”,通过重力的假说,他发现了万有引力定律。虽然我们现在知道引力并不存在,它只是时空弯曲的结果。这就是归纳法的局限之处——不能穷举实例,比如 即使你发现了一万只、一百万只天鹅是白的,你也不能断言——所有的天鹅都是白的 。通过归纳法得到的“知识”都是概然的,是一种概率,毕竟,太阳明天还能从东方升起也只是一个概率问题。因此,归纳法永远也得不到像演绎法那样保真的、有效的论证。
3.4.2 横向逻辑关系
在横向上,我们要保证每组思想必须属于同一逻辑范畴,并按照逻辑顺序进行组织 。即不能将不同的思想随意堆放在一起,而是你看到了其中的逻辑关系,才将其“挑选”出来组织在一起。实际上,大脑在进行归纳分组的逻辑分析时,会进行以下3种分析活动。
(1)时间顺序: 例如解决问题的3个步骤。
(2)空间顺序: 例如组成某公司的3个部门、化整为零(将整体分解为部分)等。
(3)程度顺序: 例如某公司存在的最严重的3个问题。
1.时间顺序
时间顺序是最容易理解的逻辑顺序,也是使用最广泛的思想分组。我们平时按照步骤(第一步、第二步、第三步……)做事就是一种典型的遵循时间顺序的活动。
例如,你负责安排一个线下活动,就可以考虑按照时间顺序,从活动前、活动中、活动后的流程思考方式入手,梳理每个流程中能做什么事,并将之拆解为可执行的细节,如图3-8所示。这种有思考方向、有条理的思维方式能让你更高效地解决工作上遇到的难题。
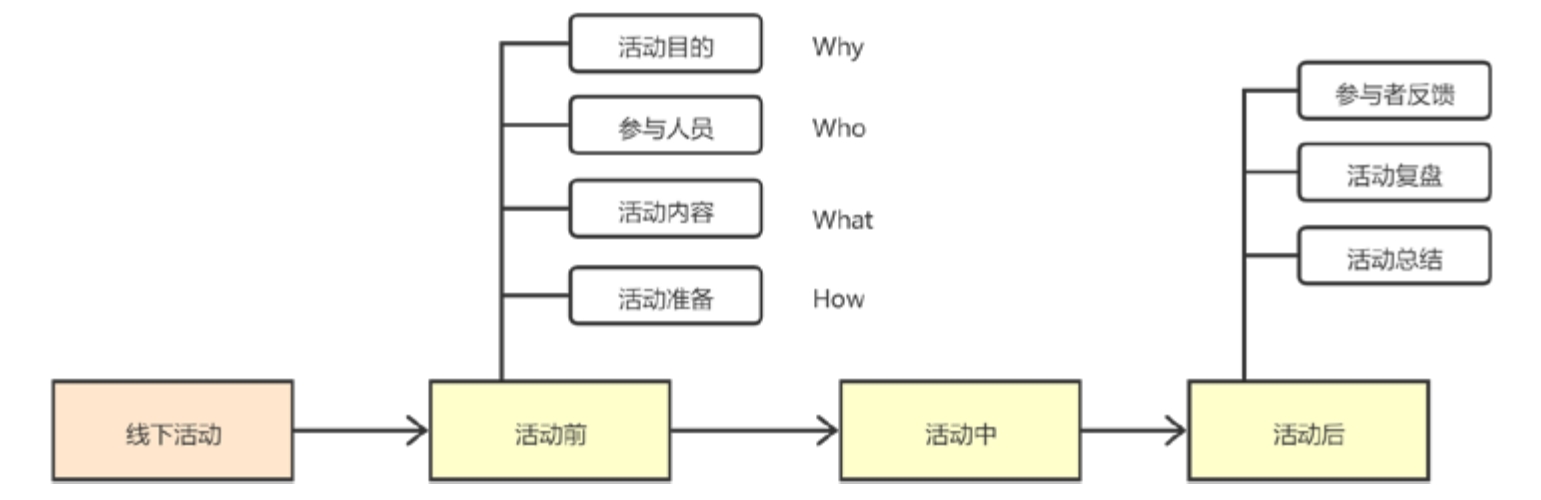
图3-8 运营活动的时间顺序
2.空间顺序
空间顺序是一种化整为零的分解,这里的空间包括实物空间和概念空间。比如我们把一台电脑拆解为显示器、主板、硬盘、显卡等组成部分,是对实物空间的分解;把农民分为富农、中农、贫农等,是对概念空间的分解。
(1)MECE原则
在将整体(不论是客观存在的,还是概念性的整体)划分为不同的部分时,我们必须保证划分后的各部分符合以下要求。
● 各部分之间相互独立(mutually exclusive),没有重叠,有排他性。
● 所有部分完全穷尽(collectively exhaustive),没有遗漏。
这两个要求的简称是MECE原则,如图3-9所示。

图3-9 MECE原则
例如,我们要对衣服进行分类,如果按照季节和风格进行分类,会出现互相重叠且不能穷尽的情况,也就不满足MECE原则。这种分类是逻辑混乱的。
我们可以按季节分:春秋装、冬装、夏装。除了这3类,再没有其他季节了,这就是穷举不遗漏,彼此之间相互独立且没有交叉,如图3-10所示。
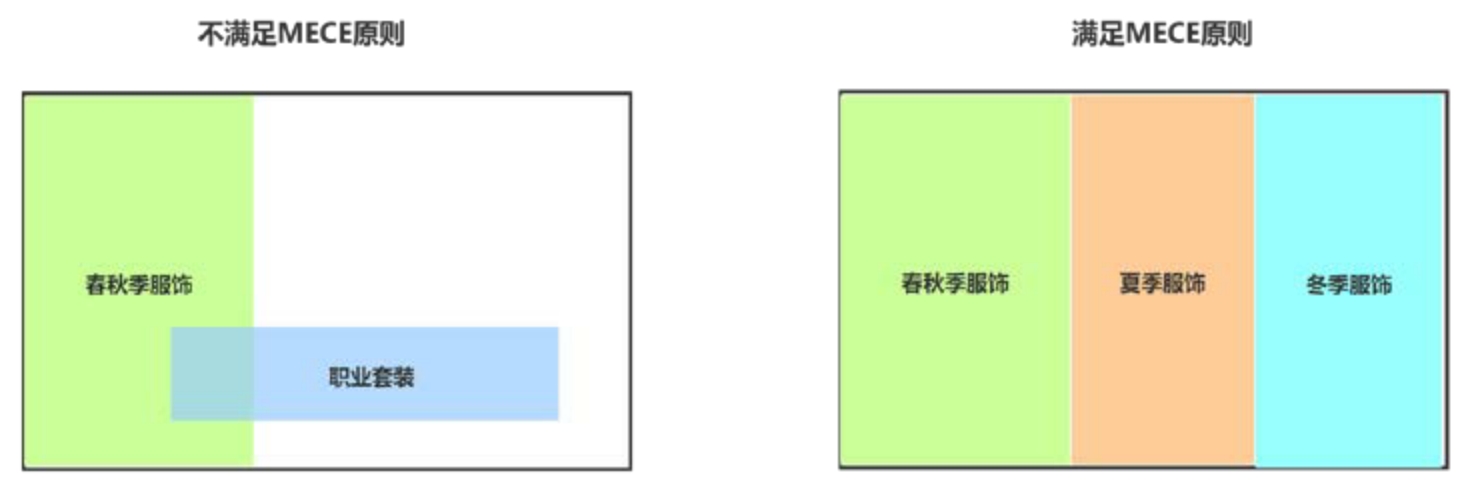
图3-10 按照MECE原则分类衣服
(2)满足MECE原则的划分方法
在做问题分解的时候,可以把待分解的问题想象成一张白纸,然后通过对折的方式对问题进行划分,能否满足MECE原则的关键在于划分维度和维度属性的选取。比如对于衣服的分类,如果选择季节这个维度,那么春秋季、夏季和冬季这3个维度属性是满足MECE原则的;但如果你只选取了春季和夏季,就是不满足MECE原则的,因为遗漏了秋季和冬季。
按照“白纸”的划分方法,我们可以有二分法、三分法和四分法。
二分法是最简单的切分,就是把“白纸”进行对折,一分为二地看待事物。比如,按照性别的不同,把人分为“男人”和“女人”;按照是否可回收,把垃圾分为“可回收”和“不可回收”;按照实用性,把木材分为“有用”和“没用”。这种方式虽然满足MECE原则,但显然过于简单了,很多事情的分类并不是简单的非黑即白,比如好人也有坏的一面,坏人可能也有善的一面。
三分法和二分法类似,都是一个维度的划分,只是选择了3个维度属性值,而不是两个。比如,按照农民收入的高低,把农民划分为贫农、中农和富农;按照综合国力,把世界分为第一世界、第二世界和第三世界。
四分法不是指在一个维度上取四等分,而是指在两个维度上,把“白纸”分为四象限。比如,按照关爱程度和控制程度,我们把父母的教养方式分为“权威型——高关爱、高控制”“专制型——低关爱、高控制”“放纵型——高关爱、低控制”和“忽视型——低关爱、低控制”,如图3-11所示。
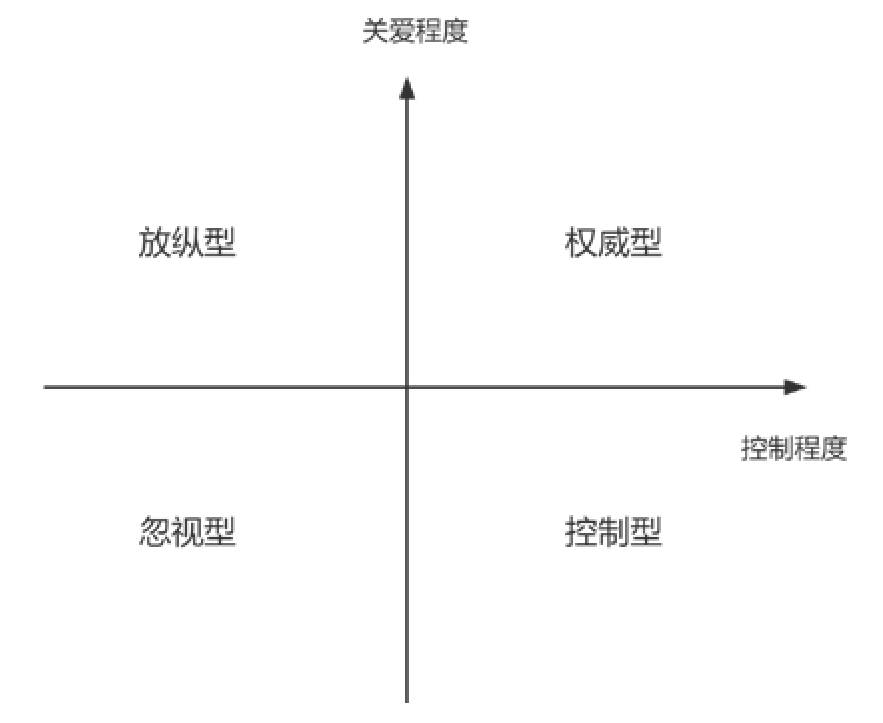
图3-11 教养方式的四分法
二维四象限的划分只适用于每个维度只有两个取值的情况。如果取值更多,那么我们仍然可以用“白纸”的方法,但已经不再是四象限了。以衣服的分类为例,假如我们既要按照季节又要按照风格两个维度分类,并且要满足MECE原则,则可以得到如图3-12所示的“白纸”划分。
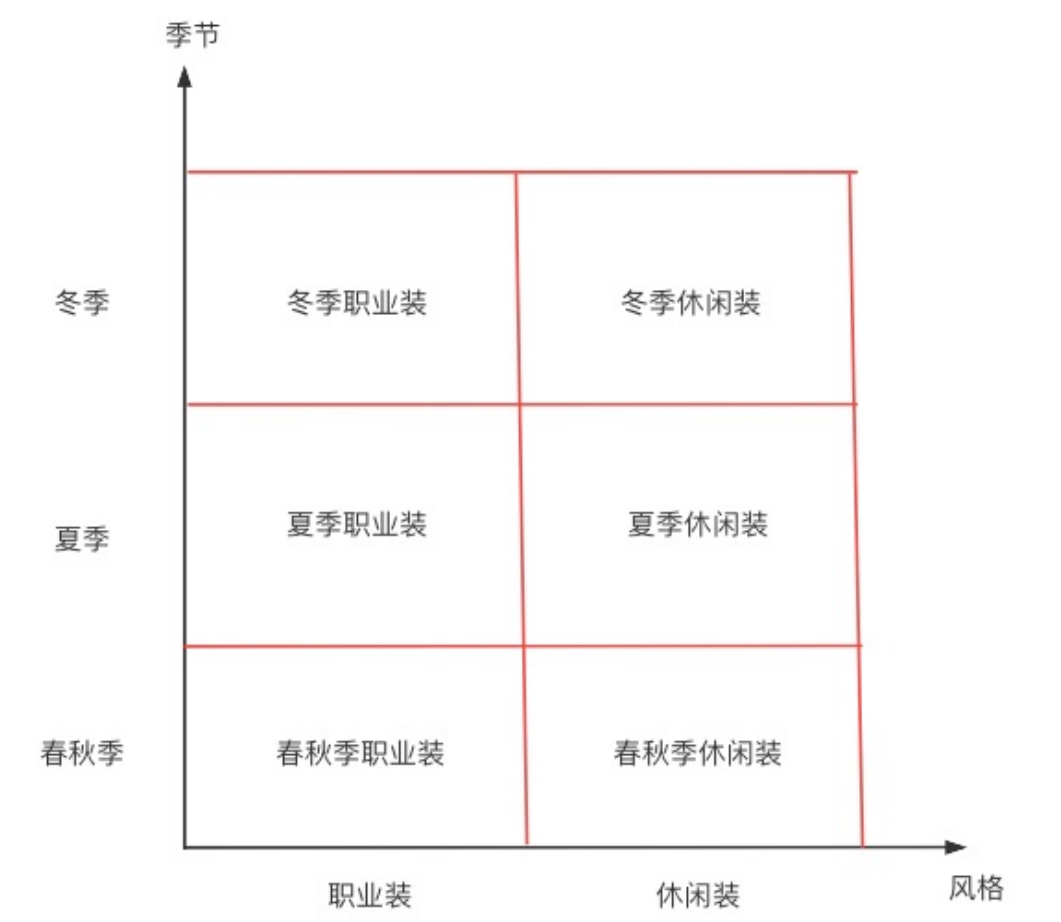
图3-12 两个维度的多值分类
当然,对于两个维度的分解,我们也可以将其转化成金字塔结构,用层次来代表维度,一层代表一个维度,两个维度就需要两层,三个维度就需要三层,以此类推。对于衣服的分类,两层就够了,分解后的结果如图3-13所示。
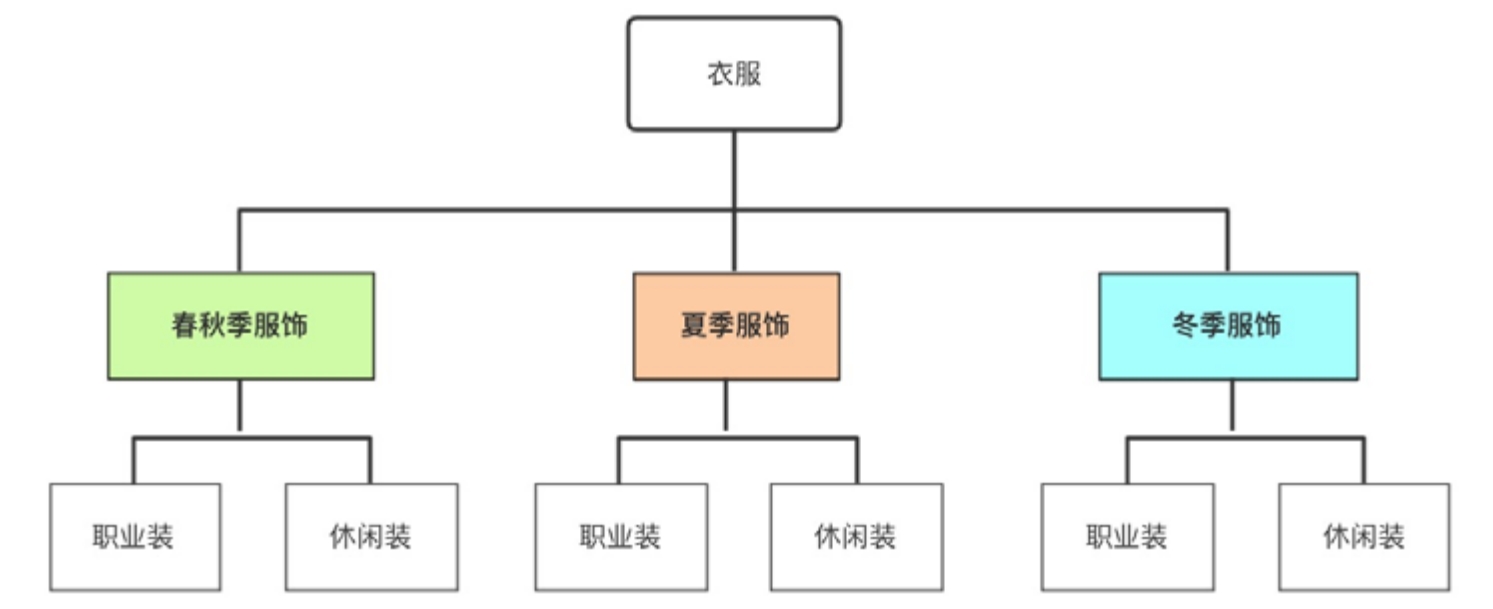
图3-13 金字塔结构的MECE分解
对于更多维度、更多维度属性值的分解,“白纸”划分法就不能胜任了,这时需要用到矩阵分析。关于矩阵分析,会在第5章中详细介绍。
3.程度顺序
程度顺序也称为重要性顺序,是指对一组因为具有某种共同特点而被聚集在一起的事物所采用的顺序。
例如3个问题、3个原因、3个因素等。假设你可能会说“这家公司存在3个问题”,这时大脑自动将这3个问题和其他问题隔开,如图3-14所示。也就是说,这3个问题是你认为这家公司存在的最严重、最迫切需要解决的问题,公司可能还存在很多其他的问题,但你只挑选这3个,因为这3个最重要。在排序的时候,最好按照先重要后次要(first thing first),先强后弱的顺序。
图3-14 程度顺序分类
逻辑是我们构建结构的底层基础,缺少逻辑的结构是经不起推敲的。在明晰了结构中的逻辑关系之后,接下来就要搭建结构,并利用结构化思维解决问题了。


