等宽比萨

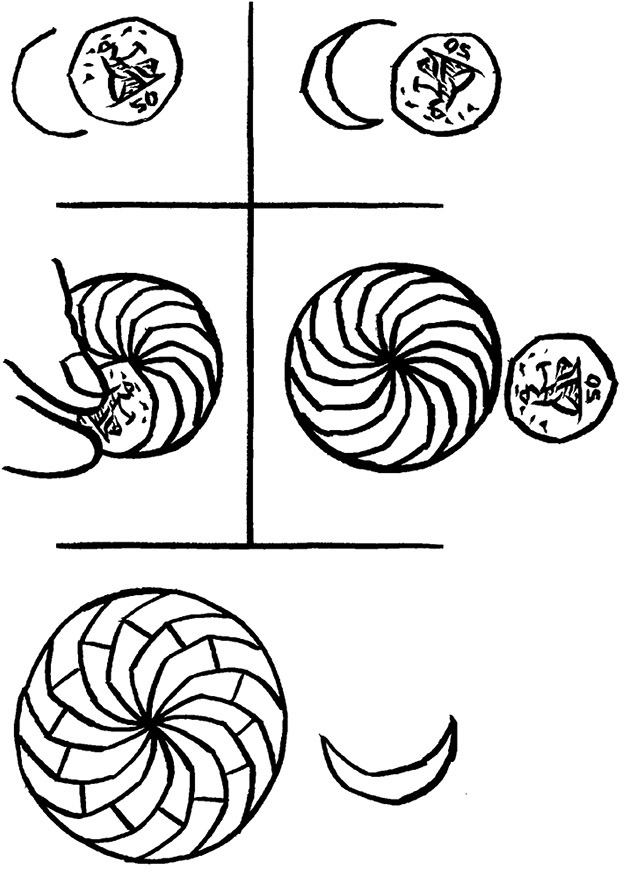
等宽图形可以帮我们解决切比萨问题吗？那些奇怪的不规则等宽图形确实不可以，但是一些规则的等宽图形可以。每个规则的奇数边等宽图形都可以给出一族解，下面我们就来尝试一个。取一枚50便士的硬币 ，在纸上描出它的4条边。然后将硬币稍微移动一下，使其中的3条边接在4条边的两端（可以完美相接），描出这3条边，然后继续描下一条边（如下图所示）。不断重复这个步骤，重复14次之后，就会得到一个整圆。这个完美的圆被分成14块完全一样的月牙状楔形。若要一些比萨块不接触中间，只需将每个楔形块切成两半即可。

让我们仔细看看这个等分比萨产生的对称楔形。它有点像正七边形，只不过其中的3条边翻转到内部变成了月牙状。这个图形被称为七边月牙（heptagrin）。任意奇数边图形都可以将它一半的边翻转到内部形成相应的多边月牙。我们最初的解法其实是将三边月牙用直线或曲线分割成两半，但每块三边月牙可以用曲线分成更多的块。用这种曲线分割法，我们也可以把其他多边月牙比萨块分成3块、4块、5块，直至无穷多块。

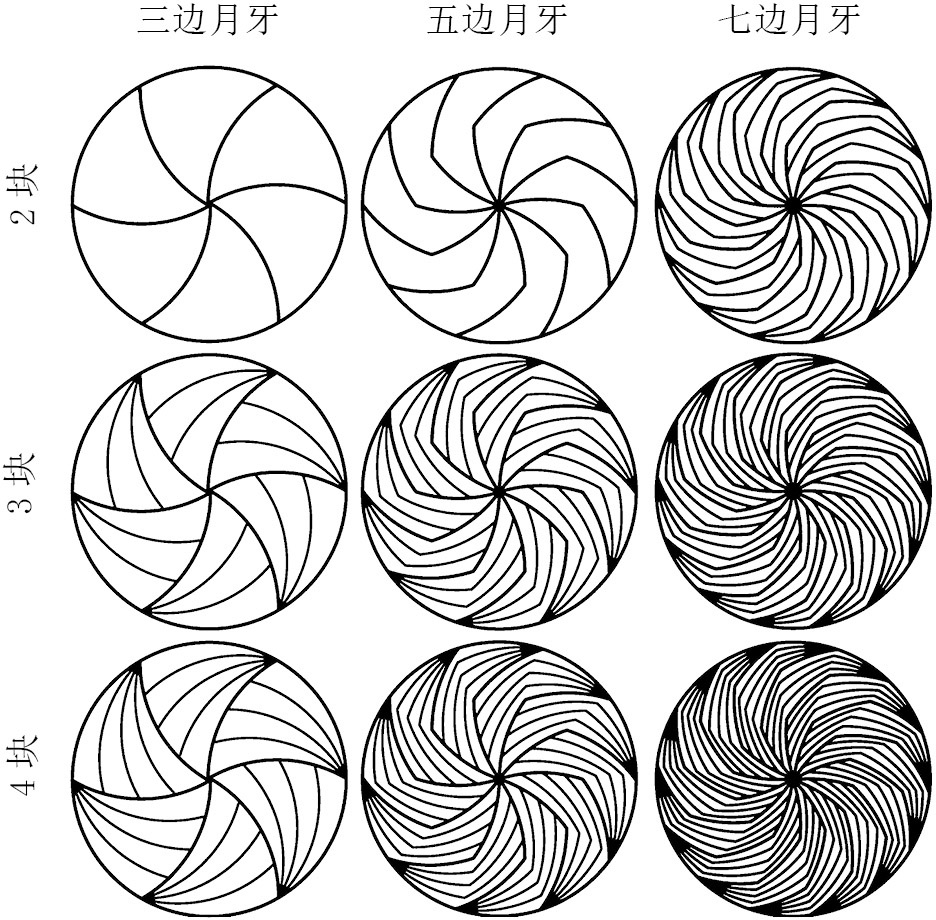
让我们来总结一下，规则的奇数边等宽图形可以给出比萨分割问题的一族解。这意味着分割比萨的方法有无穷多种，因为你总可以画出一个比现有图形多两条边的图形。不仅如此，在每种解法中，我们又可以将每个月牙块分割成任意块：2块、3块、4块……甚至无穷。因此，无穷解法的每一种又可以派生出无穷解。可见，我们切比萨的方法有无穷多种！将比萨分成42块就有两种不同的方法。（把每个七边月牙分成3块还是7块，随你选。）

你稍微试一试就会知道，为什么在比萨块不全接触中心的前提下，将比萨等分180块有5种方法，等分630块有10种方法。你还可以继续探索如何将比萨分成相同形状的块，而且只有一块不接触中心（如果你希望能让尽可能多的比萨块包含中间部分陷料的话，这种方法就很管用）。不过反过来就不行了，你不能把比萨分成只有一块包含整个中心部分，并且形状相同的块。