平面填充问题

我们首先要探究的是平面情形：将物体填充到二维平面上。即便填充区域不限制为正方形，圆作为填充图形仍然是极其糟糕的选择。因为不管怎么排列，它们之间总会留下空隙。而一些图形，比如六边形，可以无缝填充。当然，这是最高效的填充方式。装修过浴室的人都知道，所有瓷砖都可以铺满整面墙，不会留下难看的空隙。在数学中，这种用图形覆盖整个空白平面的行为称为镶嵌（tiling）。它和另外一个更为人熟悉的数学名词“密铺”（tessellation）稍有不同，后者要求镶嵌的图形种类和位置排列具有一定的规律。镶嵌不仅包括密铺，还包括随意的不留缝隙的排列。我将使用这个范围更广泛的术语。

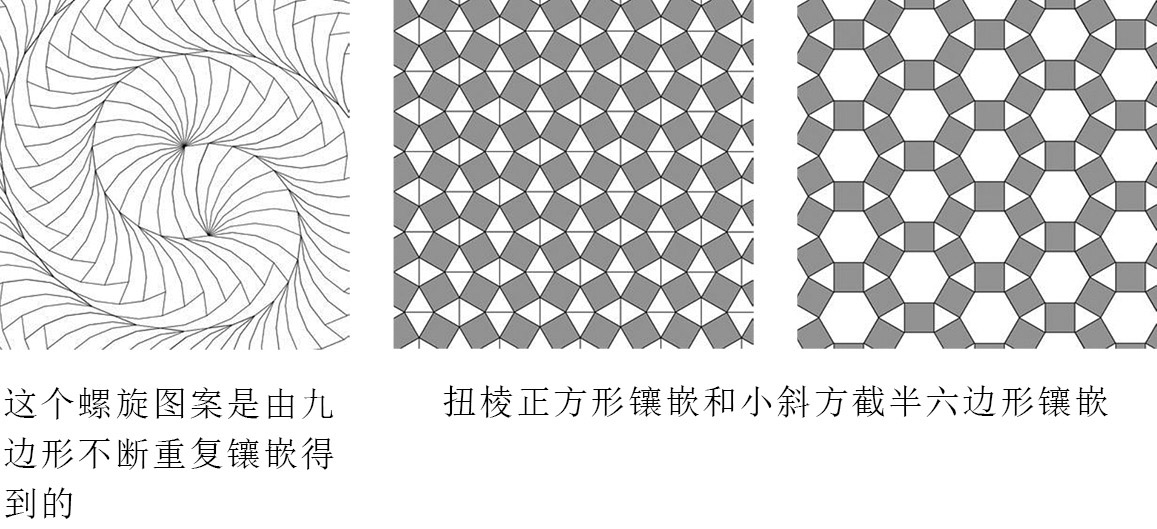
人们已经发现了许多镶嵌平面的绝妙方法，但距离发现所有镶嵌方法还有很长的路要走。有些镶嵌的方法非常无聊，比如全用正方形或者全用三角形。我们还有更好的方法。我最喜欢的一个选择是一种不规则的九边形，它能在整个平面镶嵌出螺旋图案。我们也可以使用多种图形，如正方形和三角形组合在一起可以形成扭棱正方形镶嵌（snub square tiling），六边形、正方形和三角形组合在一起可以形成小斜方截半六边形镶嵌（rhombitrihexagonal tiling，这是一个非常棒的词，但它在拼字游戏中只值36分）。知道有这么多无比绝妙的镶嵌方法之后，每当看到浴室那乏味的正方形瓷砖，我都会感到非常失望。

下面要说的这个问题是我认为从提出到解决时间相距最长的图形填充难题。这个问题的解在人类出现之前就已经存在，但直到2001年才被完全证明。这个难题就是：填充二维平面最优的形状是什么？这里的“最优”是指图形互相之间没有空隙，在周长给定的情况下，它们能覆盖最多面积。最佳的选择是六边形，而且它远在人类的数学思想萌芽前就已经被蜜蜂发现，因此这个问题被称为蜂窝猜想（honeycomb conjecture）。直到几百万年后，美国数学家托马斯·黑尔斯（Thomas Hales）才证明，不管你设计怎样怪异的边界，构造怎样疯狂的填充形状，其填充效果永远不如六边形。

与圆形相比，圆角八边形留下的空隙更大

六边形是最好的填充图形，那么有没有最差的填充图形？不幸的是，这又是一个人们还没解决的问题。我们已经知道，用圆填充平面的效果非常糟糕（在最理想的情况下，即使所有圆都紧密排列，也只能覆盖曲面表面积的90.7%），但是还有比圆更糟糕的图形——圆角八边形（smoothed octagon）。取一个八边形，将每个角替换为一段双曲线（双曲线和圆、椭圆是一家，亲密程度大约为堂表亲级别）。你会发现，不管你怎么排列，圆角八边形的覆盖率都不会超过90.24%。然而，可能还有比圆角八边形更差的图形，只是我们至今还没有发现而已。