第一章
远古科学传统
第一次世界大战结束的时候,意大利战俘营中有两位奇特的年轻人。一位是最终成为语言逻辑学大师的奥地利人维根斯坦(Ludwig Wittgenstein)。另外一位则是未及弱冠的德国人奈格包尔(Otto Neugebauer),他后来研究古巴比伦陶泥板上的数学符号,于1929年向欧洲学界作了一个令人震惊的宣布:“就算不谈应用于三角学和梯形的数式,我们还是见到复杂线性方程组的建构和解答,和巴比伦人有系统地表述二次型问题,并且肯定知道解法,而所用的计算技巧和我们的全然相当。”
 换而言之,远在公元前1800—前1600年,也就是相当于中国夏代,两河流域文明就已经产生能够系统地解决二次方程式的数学了!这个意想不到的发现大大扩展了西方学者的视野,迫使他们将自己的科学传统向古代推前一千三百年,即从古希腊推到古巴比伦。所以,我们追寻西方科学的源头不但不能够止于文艺复兴,甚至也不能够止于古希腊,而必须从远古文明开始。
换而言之,远在公元前1800—前1600年,也就是相当于中国夏代,两河流域文明就已经产生能够系统地解决二次方程式的数学了!这个意想不到的发现大大扩展了西方学者的视野,迫使他们将自己的科学传统向古代推前一千三百年,即从古希腊推到古巴比伦。所以,我们追寻西方科学的源头不但不能够止于文艺复兴,甚至也不能够止于古希腊,而必须从远古文明开始。
当然,西方远古文明不但有巴比伦,还有埃及:古埃及同样出现过有将近四千年历史的数学文献,这就是19世纪中叶发现的草纸(papyrus)数学手卷,其上所记载的算题虽然不如巴比伦数学之丰富、全面和先进,但同样显示了令人惊讶的成就,例如准确至0.6%的圆周率和截锥体的正确体积公式。远古文明所遗留下来的这些无可置疑的原始资料证明,希腊数学虽然高妙,令人赞叹,但并非凭空出现的“奇迹”,它背后是有非常久远和渊深传统的。我们在本章所要讨论的,便是这远古科学传统的具体内容,但在此之前,还需要先对这些远古文明的历史、社会与文化背景作一概述,至于它和古希腊文明的关系,则留待最后一节讨论。
一、远古文明轮廓
埃及与两河流域这两个远古文明同时起源于公元前3000年,大致上也同以公元前1000年(即埃及新王朝与亚述中期帝国结束)为下限
 。此后千余年间东地中海区域为相继兴起的巨型帝国所征服,因而逐步趋于混同。这以征服中东和埃及(公元前664)的新亚述帝国开端,波斯帝国(公元前550—前330)随其后,后者转而激发亚历山大大帝的东征和三个后继王朝的建立,最终则归于罗马帝国的大一统(约公元前30)。远古文明的科学文献主要属于公元前1900—前1600年时期,而古希腊科学的萌芽最早却只能追溯到公元前550年左右,两者在时间上相隔千年以上。因此,两者之间关系相当微妙,这将留到本章末了讨论。现在我们先为古埃及和两河流域长达两千年的历史描绘一个最简略的轮廓。
。此后千余年间东地中海区域为相继兴起的巨型帝国所征服,因而逐步趋于混同。这以征服中东和埃及(公元前664)的新亚述帝国开端,波斯帝国(公元前550—前330)随其后,后者转而激发亚历山大大帝的东征和三个后继王朝的建立,最终则归于罗马帝国的大一统(约公元前30)。远古文明的科学文献主要属于公元前1900—前1600年时期,而古希腊科学的萌芽最早却只能追溯到公元前550年左右,两者在时间上相隔千年以上。因此,两者之间关系相当微妙,这将留到本章末了讨论。现在我们先为古埃及和两河流域长达两千年的历史描绘一个最简略的轮廓。
尼罗河畔的世界
埃及是个庞大而稳定的国家:在整整两千年的漫长岁月里,它虽然经历多次外族入侵和主权更迭,但大体上能够维持文化认同,以及在绝对王权下的政治一统。这和它的半封闭地理环境有本质关系——它的西边是大沙漠,北边是海,南边是崎岖高原,东边是沙漠、山岭和海的组合,只在东北有干旱困阻的对外通道。它的这些地理特点和西方其他文明——巴比伦、希腊、罗马截然不同,甚至恰恰相反。就这一点而言,它在西方文明中是独特的。但对于中国人来说,这些却再也熟悉不过,因为传统中国同样具有半封闭地理环境、稳定文化认同,以及大一统王朝等特征。
和中国不同的是,埃及非常幸运,从最早期开始,就留下了大量文字记载,包括刻在石头上的象形文字(hieroglyphic),以及写在草纸上的僧侣行书体文字(hieratic glyph)和大众体文字(demotic glyph),其性质遍及碑记、历史、叙事、训诲、教材、文学作品、税收和其他行政、管理档案。在干燥的沙漠空气中,特别是在牢固和密封的墓室里面,有大量这类宝贵记录完整地保存下来,因此由祭司曼尼韬(Manetho)编纂的传世帝王古史可以从多个出土文献得到印证,这包括现存西西里的巴勒莫残石(Palermo Stone)帝王纪事碑(公元前2400)、现存都灵的草纸本帝王表(Turin Canon,公元前1300),以及稍后一百年左右的塞卡拉墓刻碑(Saqqara Tablet);至于其各个时代的具体状况,则可以从大量的纪功碑和大臣、总管的墓室自叙与诏令抄录而得以考究。上文提到的“数学手卷”属于草纸本数学教材和计算记录,它十分稀罕,却为当时不那么受注意的文化面向提供了确实证据。
从这些记录得知,“王朝早期”(公元前3100—前2686)是埃及从众多独立小邦融合成为一统政治体的时期,在其间它发展出交错盘结的文化、生产、政治和宗教体制,这包括:以上述两种字体书写的文字、在尼罗河周年泛滥所带来的肥沃土地上的农耕,还有以法老(Pharaoh)绝对王权为中心的层级化官僚体系、多神崇拜、死后的复活与永生追求等等。当然,最重要的是与王权紧密结合的宗教体系,这包括众多和繁复的祭典、庞大和复杂的祭司组织,以及神庙、陵墓、金字塔等硕大无朋的建筑。这样,强有力的一统王朝遂首先在南方的“上埃及”即底比斯(Thebes)一带出现,其后它吸纳了北方的“下埃及”诸邦,并且为统治需要而将行政中心向北迁移到尼罗河三角洲顶端的孟菲斯(Memphis),从而迎来了“旧王朝”,为埃及的历史时期揭开序幕。
表1.1 古埃及历史分期
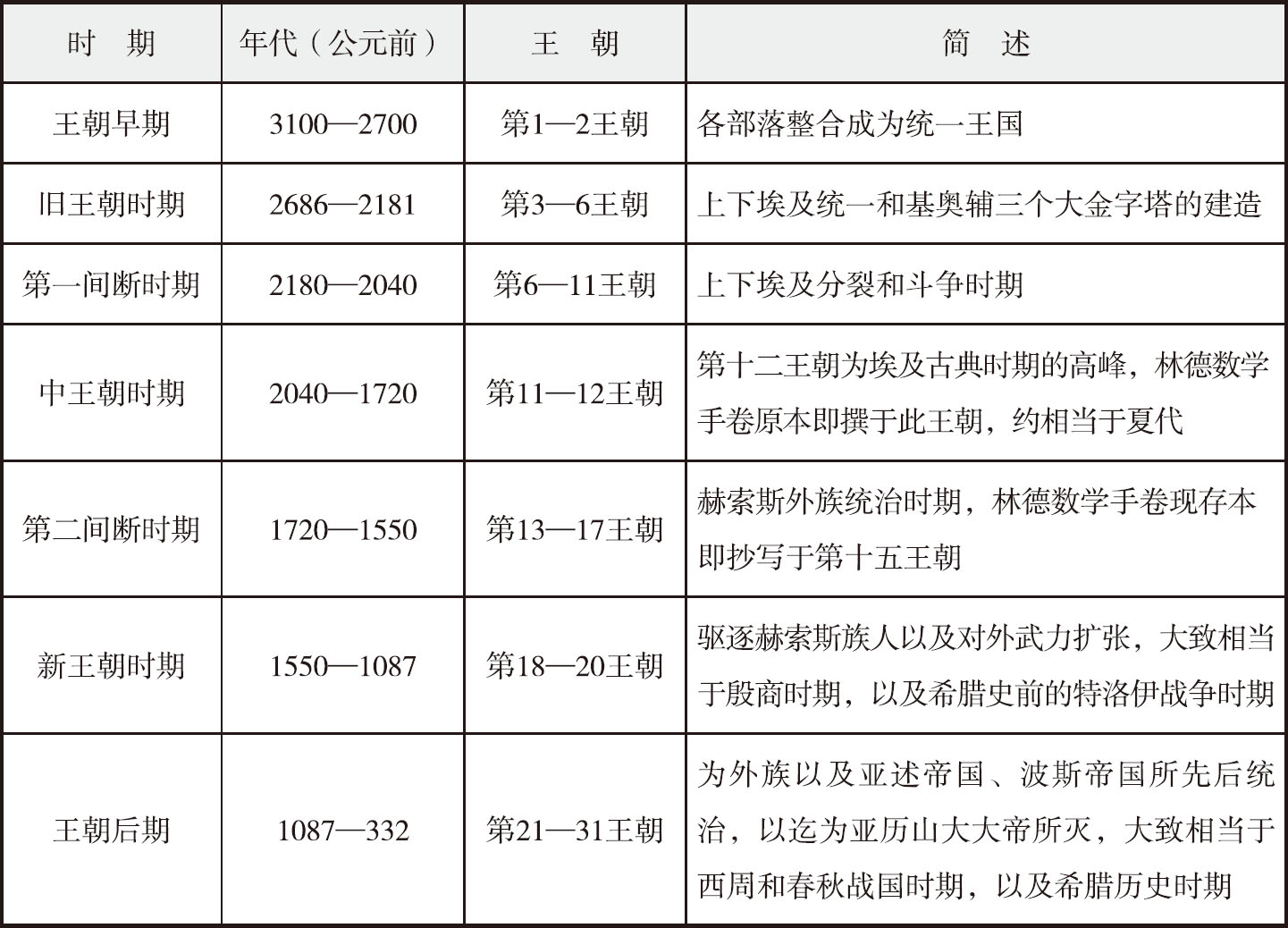
古埃及历史前后跨越三千余年,包含31个王朝,共分七个时期,表1.1为它提供了一个梗概。这段历史值得注意的有以下几点。首先,如今仍然矗立的三个基奥辅(Cheops)巨型金字塔建造于旧王朝早期,也就是说王朝的宗教信仰、政治控制和技术力量从头就已经高度发展。其次,近年研究显示,和以往印象相反,王朝虽然需要动员大量民众来开展庞大建造工程,但这并非以高压奴役手段执行:在工地上不但民众的生活得到照顾,而且经济上市场贸易在起相当作用——否则,如此庞大的建造体制不可能持久。第三,尼罗河农业虽然是埃及经济的核心,但采矿、冶炼、对外贸易也同样重要。第四,从旧王朝以至中王朝和新王朝,埃及的体制、组织和经济、军事力量并没有停滞,而是一直在持续扩展、壮大。因此到了新王朝它开始有能力越过西奈半岛,向巴勒斯坦扩张。但很可能也正是这种扩张触发了亚述、波斯、希腊和罗马这些新兴力量的先后入侵和占领,从而导致它作为一个独立文明的衰亡。此外,我们得强调:在希腊进入历史时期(这大致可以以奥林匹克竞技在公元前776年开始为标记)之际,古埃及已经进入王朝后期,也就是接近尾声了。因此古希腊哲人、历史学家仰慕其历史之悠久、蕴藉之深厚,是非常自然的。最后,埃及最令人感到神秘、震撼之至的事物——金字塔、木乃伊、神庙等等——显示在追求永恒生命的强烈欲望驱使下,人可以发挥如何巨大力量,而这种欲望和力量也可能是了解其他文明现象的关键。
断裂的两河流域文明
两河流域文明和古埃及文明表面上颇为相似:两者都是以大河为中心的农业文明,同样出现了高度集权的一统王朝和强大宗教力量,两个文明同样古老、悠久,都延续到亚历山大大帝时代才先后为马其顿和罗马帝国所吞并。然而,它们其实有深层差异,最根本的,就是埃及文明是连续、整体、一元的,两河流域文明则是断裂、分立和多元的,前者和中国相似,后者则接近西方。因此,埃及文明虽然包含多个王朝和时期,但其文字、文化、体制则始终没有大变化,其中心也只是在底比斯和孟菲斯之间摆动。两河流域文明则不然,它分属苏美尔、巴比伦和亚述等三个帝国时期,这些帝国是由使用不同语言的不同民族在不同政治中心所建立,它们的宗教、文化虽然相互传承,但各有不同本体,是不可混淆的——这是时间上的断裂。不但如此,与此三个帝国同时并存,相互攻伐、影响的,还有周边或大或小的许多其他民族和政权,例如东边的埃兰(Elamites)和波斯(Persia)政权、北部的胡利安(Hurrian)和古梯(Gutian)政权、西北部的赫梯(Hittite)王国、西部的阿摩利(Amorite)政权等等。其实,它最早期的苏美尔帝国本身,就已经是多个城邦的松散结合体,其主宰性力量始终在不同城邦之间转移,嗣后阿卡德人(Akkadian)和亚述人(Assyrian)之先后入主,可以说是同一模式的扩大——这是空间上的分立。
也许,这种强烈对比可以从地理环境的差别找到解释。毕竟,两河流域是“四战之地”:它东边的扎格罗斯(Zagros)山脉、北边的高原、西边和南边的沙漠好像是自然边界,但并不构成有效屏障,其后面的其他民族、政权可以通过无数山脉缺口、途径入侵,使得此地始终处于动荡、风暴之中,而这正是自古至今所不断发生的事情。
在19世纪以前西方人所知道的中东历史主要从圣经《旧约》得来,基本上仅限于后期亚述帝国。其后,经过将近一个多世纪的努力,即到20世纪中叶,两河流域的丰富历史,才得以揭露于世人之前。这转变的关键在于中东发现了陶泥板(clay tablet)上以楔形文字(cuneiform)书写的大量文献。这些陶泥板经过晒干或者烧烤之后非常坚固耐久,成为几乎是永久的记录。我们今日对两河流域远古文明的认识,绝大部分就是得之于收藏在各大博物馆中的数十万块陶泥板。更为幸运的是,这些陶泥板有相当数量和科学特别是数学有密切关系,它们所提供的资料,要比埃及那绝无仅有的五六个草纸手卷丰富太多了。
苏美尔文明
历史上的苏美尔(Sumer),是指今日伊拉克南部,即从巴格达到波斯湾之间的两河流域。它从公元前5000年前开始,就已经有连续发展的农业文明,在此文明末期,出现了以图形符号记录实物的方法(公元前3500—前3200),以及由之发展而来的楔形文字(公元前3200—前2900)。所谓“苏美尔人”,可能就是在此时从里海附近的阿拉塔(Aratta)移居两河流域,从而刺激当地产生高等文明。除了文字以外,这一文明的特征还包括人口密集的城市、大规模灌溉种植、结构繁复的大神庙、精美和风格奇特的巨瓶和圆柱形印章,以及频繁的远程贸易等。比对埃及,苏美尔文明最不同的无疑是它以多个城市而并非固定首都为核心,以及贸易在其经济体系中占据的重要位置。有学者认为,苏美尔文明是经过长久酝酿而逐渐发展出来的本土现象,古埃及文明则是由外来典范刺激而萌生的衍生现象,而外来刺激的唯一可能来源,当然就是苏美尔文明
 。
。
苏美尔文明前后延续近千年之久(公元前2900—前2000),一共经历了城邦争长、霸主出现、阿卡德王朝,以及权力和文化达到顶峰的乌尔(Ur)王朝等四个时期(表1.2)。它的发展有以下几条线索。首先,是政权的逐步集中;其次,是以大神庙为中心的多神宗教之发达并且与政权密切结合;第三,是官僚组织之日趋精密和庞大;最后,则是法律体系包括各种商业契约、协议的逐渐完备。而作为所有这些发展基础的,则是楔形文字的发展和书写在陶泥板上文献的大量应用。和中国一样,苏美尔也是“文字之邦”,但他们幸运得多,因为上天赋予了他们极其方便而且几乎是“不朽”的记录方法。
表1.2 两河流域历史分期
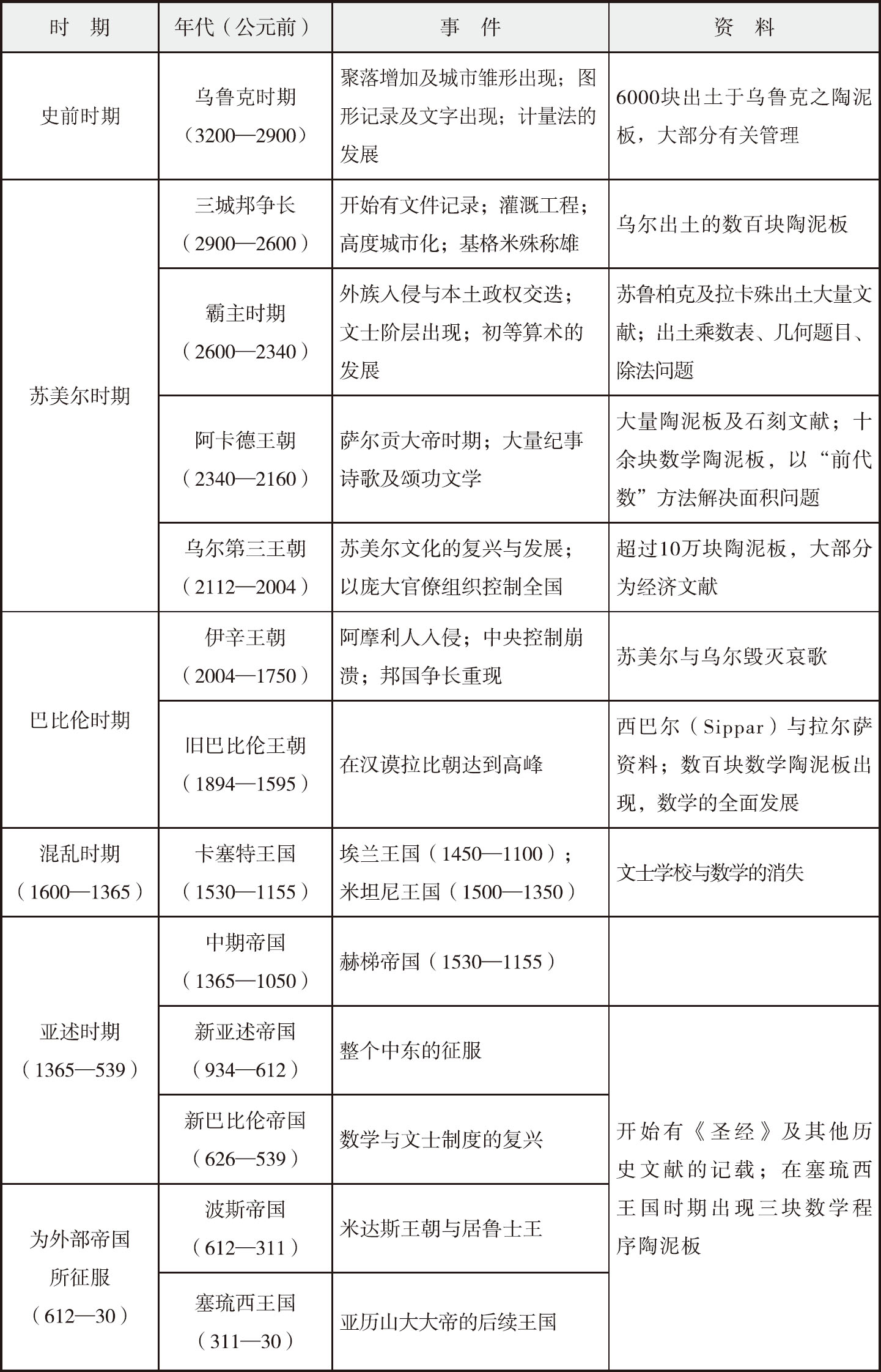
这确切的记录使得两河流域在相当于中国三皇五帝时期就已经进入信史时代。例如,苏美尔第一英雄基格米殊(Gilgemesh)的时期相当于公元前2600年,他不但作为主角出现于刻录在陶泥板上的史诗中,而且,和许多更早的君主一样,有早期文献记载,那就是公元前1800年的“帝王表”(The King's List),以及公元前2000年的神庙碑刻,即列出神庙建造者或者重修者的所谓“Tummal Inscription”。而且,从最早期开始,就已经出现了大量买卖契约;上述霸主时期的拉卡殊城(Lagash)乌鲁卡基那王(Urukagina,约公元前2350)留下了一份长达数千字的政治改革文告;到乌尔第三王朝,不但开创君主乌尔南姆(Ur-Nammu,约公元前2060)留下了残缺但也许是人类最早的成文法典,而且王朝百余年间的民事、刑事诉讼档案以及公证文件也都留存下来,使得我们可以获知当时法律程序的梗概。最后,到了伊辛(Isin)王朝亦即旧巴比伦帝国前期,则有利皮伊殊塔王(Lipit-Ishatar,约公元前1930)另一部颇为完整的法典。
和古希腊一样,苏美尔文明以城邦为基本政治形式,建立庞大帝国非他们所长。正如初次统一希腊诸邦和古代世界的亚历山大是马其顿人而非雅典或者斯巴达人,同样,在两河流域初次建立帝国的萨尔贡大帝(Sargon the Great,约公元前2340)也并非苏美尔人,而是说阿卡德语的闪米特族人(Semite)。在这使用苏美尔文字,但语言不同的外族政权之后,出现了苏美尔人的黄金时代,即乌尔第三王朝,严密而全面的官僚统治在其时达到高峰。但仅仅百年之后苏美尔文明就告结束了。
巴比伦文明
苏美尔文明之后,以阿摩利人为主的伊辛王朝代兴,它前后经历二百零三年和十四位君主,以迄被巴比伦的汉谟拉比所灭。在此时期多城邦政治形态继续留存,与拉尔萨(Larsa)、巴比伦、亚述、马利(Mari)等许多政权同时并存,以迄为所谓旧巴比伦王朝(Old Babylonian Dynasty,约公元前1900—前1600)所取代。此王朝前后历十一王,著名的汉谟拉比(Hammurapi,公元前1792—前1750)居第六位。他在位的时间极长,所征服的幅员很广(包括伊辛王国),以刻在黑石柱上而留存后世的《汉谟拉比法典》(原物现存卢浮宫博物馆)知名。但这其实并非他原创:如上文提到,在其前两三百年间,已经最少有过两套成文法典出现了。此外,由于还不十分清楚的原因,从他的统治开始,数学陡然兴盛发展,今日出土的绝大部分数学陶泥板都属于公元前1800—前1600年这两百年间;更令人惊讶的是:上一节所提到的埃及数学手卷,也同样属于此时期。这是巧合,抑或有更深层关系存乎其间,目前还没有办法判断。
巴比伦帝国没有维持霸权很久,在汉谟拉比之后就开始慢慢衰落,以迄被崛起于小亚细亚的赫梯王国所灭。在随后大约千年间(公元前1600—前600),经历了卡塞特人的长期入侵,以及埃兰人、赫梯人和胡利安人政权相继兴起之后,两河流域的政治重心北移到底格里斯河上游的亚述和尼尼微(Niniveh),受武力和版图都达到空前地步的亚述帝国所主宰。在这漫长时段,文士学校制度被废除,数学完全归于沉寂,几乎没有任何相关陶泥板留存。这样要待到新巴比伦王朝(亦即所谓迦勒底巴比伦,Chaldean Babylon)的短暂复兴,才再有一些数学陶泥板出现,它们显示出与远古传统的联系,但并没有新进展。在公元前529年,新巴比伦王朝为波斯帝国所征服,其后中东又相继为亚历山大大帝和罗马帝国所征服,两河流域作为独立远古文明的阶段就结束了。
二、埃及数学手卷
宗教主宰埃及文明,埃及人可以为神灵以及身后世界而奉献此生。相比之下,科学显得很渺小,可以说微不足道,最多不过是诸般实用技术的附庸罢了。把埃及两千多年间所遗留下来的极少数科学文献和它浩如烟海的其他文献相比,我们自然不免涌起这样的感觉。不过,即使如此,这些远古文献仍然埋藏了两个令人非常惊讶的成就。首先,是其一度采用的圆周率π≈3.16准确到0.6%,和东汉刘歆、张衡,三国时代王蕃等所求得值的准确度(0.4%—1%)不相上下,一直要到魏晋南北朝的刘徽、何承天方才超越此成就
 。其次,是文献中已经提出了截锥体(frustum)体积的准确公式,而这即使在以几何学见长的古希腊数学中,也是要到公元1世纪才明确提出来的。因此,古埃及数学到底曾经达到何种水平,还不能够轻易判断。
。其次,是文献中已经提出了截锥体(frustum)体积的准确公式,而这即使在以几何学见长的古希腊数学中,也是要到公元1世纪才明确提出来的。因此,古埃及数学到底曾经达到何种水平,还不能够轻易判断。
林德数学手卷
从18世纪末年开始,法、英两国相继从奥图曼帝国手中夺取了埃及的控制权,自此之后这古国的遗迹和文物便吸引了大批西方官员、商人、探险家和学者。在他们所发掘、搜集、购得的无数器物、文献之中,有六件写在草纸或者羊皮上面的数学手卷,其中最重要、最有价值的,是所谓“林德数学手卷”(Rhind Mathematical Papyrus,RMP)
 。它是苏格兰律师和埃及学家林德(Alexander Henry Rhind)于1855—1857年在底比斯的卢克索(Luxor)大神庙附近发掘陵墓时所购得,他去世后由大英博物馆在1865年分两截购入收藏,连接这两截的片段则为纽约布鲁克林博物馆(Brooklyn Museum)收藏。这手卷宽32厘米,长513厘米,由14张40厘米×32厘米的草纸页片粘连而成,除了稍有残缺以外,大体保存完整光洁。手卷是用红黑两色在正反两面书写,字体端庄工整,内容包括誊录者阿莫斯(Ahmose)的题注、85道算题,以及一个数表(
图版1
)。
。它是苏格兰律师和埃及学家林德(Alexander Henry Rhind)于1855—1857年在底比斯的卢克索(Luxor)大神庙附近发掘陵墓时所购得,他去世后由大英博物馆在1865年分两截购入收藏,连接这两截的片段则为纽约布鲁克林博物馆(Brooklyn Museum)收藏。这手卷宽32厘米,长513厘米,由14张40厘米×32厘米的草纸页片粘连而成,除了稍有残缺以外,大体保存完整光洁。手卷是用红黑两色在正反两面书写,字体端庄工整,内容包括誊录者阿莫斯(Ahmose)的题注、85道算题,以及一个数表(
图版1
)。
根据题注中的阿莫斯自述,他是在所谓“赫索斯”(Hyksos)时期第十五王朝(公元前1648—前1540)的阿波菲斯王(Apophis)第三十三年誊录此卷的;所誊录的,是第十二王朝第六王阿门尼米斯三世(Ammenemes Ⅲ,公元前1843—前1798)的旧卷。从这相当清楚和仔细的记载,我们可以肯定这手卷是公元前1600年左右的抄本,其所根据的原本则写成于公元前1800年左右,距今将近四千年了。
表1.3 林德数学手卷算题内容综述
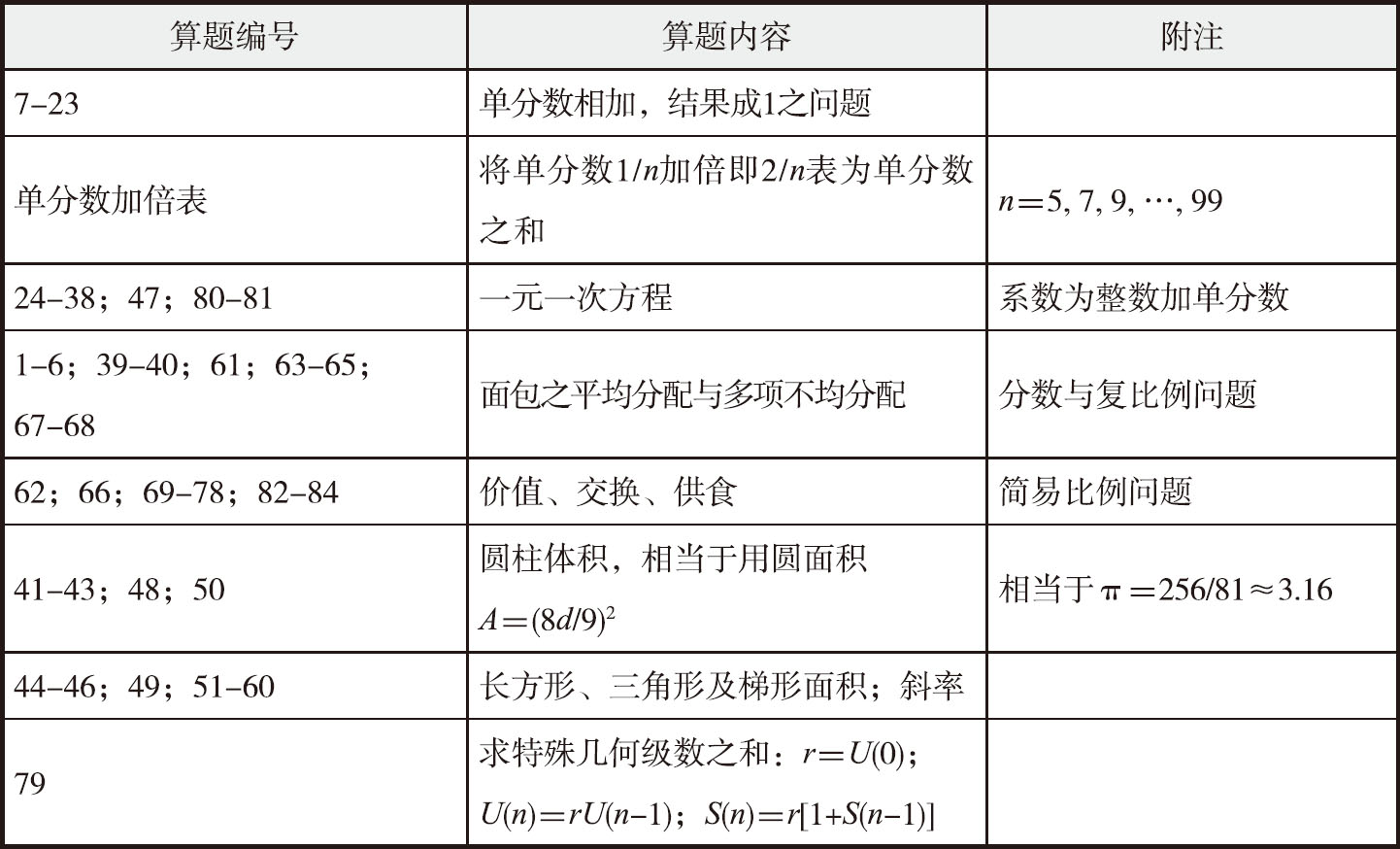
从表1.3可见,此远古数学手卷的性质类似于教科书,内容大体上可以分成分数运算、比例问题、一元一次方程和几何形体求面积、体积等四类,性质大都很浅显,但也有以下值得注意的地方。第一,古埃及的乘法和除法基本上都分别是以加法和减法来演算的,也就是说,他们还没有发展出应用乘数表和对位的方法。第二,他们虽然已经有分数的观念,并且广泛应用,然而却还没有发展出普通分数(common fraction),即以分子和分母两个数目表示一个分数的观念,而局限于“单分数”(unit fraction),即是分子为1的分数1/ n (2/3的应用是个特殊例外)。这种执着使得他们在分数的运算上发展了许多奇特的技术,其中最显著的,便是如何将单分数的双倍,分解为其他不同单分数之和(这不一定是独特分解),例如2/11=1/6+1/66,2/71=1/40+1/568+1/710,等等。手卷中的数表便是为5—99之间所有奇数 n 的单分数倍数2/ n 列出分解的方式。
第三,所有比例和复比例题目,都和食物、物件的分配,或者购买价格有关;至于一元一次方程也往往是和(最少表面上的)应用题相关。但从数学技巧上来说,这两类题目的重点都在于处理分数的技巧,而由于他们对单分数的执着,这些技巧是颇为特别的。第四,所有几何题的目标主要是计算简单形体的面积或者体积,这包括正方形、长方形、梯形、圆形的面积,以及长方柱、圆柱的体积,此外也引进了斜率的概念。特别值得注意的是,它用以计算圆面积
A
的方法相当于下列公式:
A
=(8
d
/9)
2
,其中
d
是直径。这相当于圆周率π的有效值是256/81≈3.16,其准确度已经达到0.6%。至于当时怎么能够获得这样高度近似的数值,则从该题的附图引起了各种可能猜测,但迄今没有定论
 。可惜的是,到后来这方法好像失传了,粗略的π≈3反而应用更广。第五,手卷中还有一道很奇特的几何级数求和问题——但它只是在级数首项和级数比率相等的特殊情况下求和,所以意义并不是很大。
。可惜的是,到后来这方法好像失传了,粗略的π≈3反而应用更广。第五,手卷中还有一道很奇特的几何级数求和问题——但它只是在级数首项和级数比率相等的特殊情况下求和,所以意义并不是很大。
莫斯科数学手卷
林德所发现的,同时还有一个年代相若的羊皮手卷,它已经硬化和黏结,一直到1927年才打开,然而结果却令人大失所望,因为它只不过是誊录了26道单分数加法题,是常用手册、数表之类的东西
 ,并没有特殊价值。重要得多的是“莫斯科数学手卷”(Moscow Mathematical Papyrus,MMP),它在1893年由俄国人戈列尼谢夫(V. S. Golenishchev)从埃及人拉苏尔(Abdel-Rasoul,此人曾经发现秘密陵墓和大量帝王木乃伊)手中购得,后来归莫斯科艺术博物馆所有。此卷长度与林德数学手卷相若,但高仅8厘米,也属第十二王朝旧物,但年代更早,约在公元前1890年。不幸的是,誊录者很草率,卷子又颇为残破,所录25道算题有将近三分之一破损或者隐晦无法阅读,其余各题则大多是浅易的交易、比例、面积计算题等,并没有超出林德数学手卷的范围
,并没有特殊价值。重要得多的是“莫斯科数学手卷”(Moscow Mathematical Papyrus,MMP),它在1893年由俄国人戈列尼谢夫(V. S. Golenishchev)从埃及人拉苏尔(Abdel-Rasoul,此人曾经发现秘密陵墓和大量帝王木乃伊)手中购得,后来归莫斯科艺术博物馆所有。此卷长度与林德数学手卷相若,但高仅8厘米,也属第十二王朝旧物,但年代更早,约在公元前1890年。不幸的是,誊录者很草率,卷子又颇为残破,所录25道算题有将近三分之一破损或者隐晦无法阅读,其余各题则大多是浅易的交易、比例、面积计算题等,并没有超出林德数学手卷的范围
 。
。
但是,它有两题却非常特别,显示出意想不到的几何计算能力。这首先是第14题,它正确地提供了计算截锥体,即金字塔截去尖端而成为平顶立体的体积公式:
V
=
h
(
a
2
+
ab
+
b
2
)/3,其中
h
是截锥体高,
a
和
b
分别是底正方形和面正方形的边长。这是个不那么容易得到的准确公式,在古希腊数学中要一直迟到1世纪的赫伦(Heron)才初次提出来。对于古埃及人如何得到这个公式的有不少猜测,例如,他们肯定知道完整金字塔的体积是底面积乘以高除以3;根据这个公式,只须将大金字塔体积减去塔尖那个小金字塔的体积,原则上就可以得到截锥体的体积;他们也可能把截锥体分解为小金字塔、方棱体和两个三角棱体,然后求其体积之和。但是,要以这类方法得到上述公式的话,必须做相当繁复的数式运算,在符号代数还未曾出现的时代,这是极端困难的
 。
。
其次,它的第10题是计算一个“开口篮子”的面积。倘若将此视为半球的表面积
A
,那么它提出了正确的公式:
A
=2π
r
2
,其中
r
是半径,π的相当值同样是前述的256/81。倘若真是如此,那么远在阿基米德之前一千五百年,埃及人就可能已经知道(虽然并没有证明)他最可引以自豪的成就之一,即球表面积公式了!这无疑非常令人震惊,它有两种可能解释:其一是编织草篮子是普遍日常工作,所以埃及人可能从经验上知道,近乎半球面的篮子面积大致是其圆形开口面积π
r
2
的两倍;另外一种看法是所谓“篮子”其实是半圆柱面,而计算所得也可以解释为其面积,但这似乎就比较牵强了
 。
。
其他数学手卷
除了上述两个主要草纸卷以及一个羊皮卷之外,余下的其他三个数学手卷年代也在公元前1900—前1800年间,但它们所提供的资料很稀少
 。大英博物馆所藏的“卡洪数学手卷”(Kahun Papyrus)只剩六块残片,它有部分和林德数学手卷相同,此外有计算圆柱体积的问题,以及涉及开方的问题。柏林国家博物馆(Staatliche Museen,Berlin)所收藏的“柏林数学手卷”同样是一组残片,它似乎和毕达哥拉斯定理或者二元二次方程式有关,不过其确切意义目前只能够存疑。最后,藏于波士顿美术博物馆(Boston Museum of Fine Art)的“莱斯纳数学手卷”(Reisner Papyrus)则大部分是工场记录,只有小部分和建筑施工,即挖掘体积的计算有关
。大英博物馆所藏的“卡洪数学手卷”(Kahun Papyrus)只剩六块残片,它有部分和林德数学手卷相同,此外有计算圆柱体积的问题,以及涉及开方的问题。柏林国家博物馆(Staatliche Museen,Berlin)所收藏的“柏林数学手卷”同样是一组残片,它似乎和毕达哥拉斯定理或者二元二次方程式有关,不过其确切意义目前只能够存疑。最后,藏于波士顿美术博物馆(Boston Museum of Fine Art)的“莱斯纳数学手卷”(Reisner Papyrus)则大部分是工场记录,只有小部分和建筑施工,即挖掘体积的计算有关
 。
。
总括而言,从以上六个手卷所能够看到的古埃及数学大部分都很浅易。然而,它显然也并不缺乏高深和精密部分,只是由于证据稀少,所以它在漫长的两三千年岁月中,到底发展到什么程度,实在难以判断。此外,对埃及计算数学的重要性也有不同的估计,例如古希腊数学史专家希斯(Thomas Heath)就曾经论证,在几何与代数两方面,希腊数学都渊源于埃及,而林德数学手卷上的计算题就已经具有解一次方程式的雏形
 。
。
三、陶泥板上的数学
埃及数学手卷的发现是非常偶然而稀罕的,因此我们无法衡量埃及数学的真正水平。两河流域的数学却完全不一样。从19世纪末叶开始,通过长期考古发掘,已经有大量载有远古楔形文字记录的陶泥板出土和累积在西方各大博物馆中,其中大约400块已知和数学有关系。这些数学陶泥板的研究,是由开山祖师奈格包尔奠定基础。在20世纪初,陶泥板上的大量数字、数表到底有何意义还是个谜,这位德国哥廷根大学才华横溢的青年数学家接受了挑战,从学习以楔形文字书写的阿卡德语开始,经过数年潜心研究,终于破解谜团,从而作出本章开头所引述的震撼性宣布。在其后不久,和许多其他德国学者一样,他也由于纳粹当权而移居美国,并出任布朗大学(Brown University)教授,该校科学史系在近半个世纪能够大放异彩,他的领导、培育之功实不可没。
但开拓先锋奈格包尔所揭露的,其实只是冰山一角而已。经过随后许多学者大半个世纪的辛勤研究,巴比伦数学的整体面貌,特别是其几何型代数学的精妙与丰富,方才为学界充分认识,并且由丹麦科学史家海鲁普(Jens Høyrup)在《长度、阔度、平面:旧巴比伦代数及其支属的面貌》一书中全面展示于世人之前。我们这才知道,三千五百年前巴比伦数学所达到的水平,所显示的运算能力,其实远远超过一般学者想象,而且,如下文将会讨论的,古希腊乃至中古伊斯兰数学的渊源,都有可能直接追溯到古巴比伦
 。
。
西方数学的起源
两河流域的数学有个悠久和渐进的发展过程,它的第一阶段是苏美尔文明的数学,那主要是发展记数法和算术。这在它的数学陶泥板上显示得非常清楚:在最早期出现的,是用以记录不同实物数目的各种符号;到了乌鲁克(Uruk)考古时代末期(公元前3200—前2900),这些符号逐步统一和抽象化,以至演变为有独立意义的数目字,而文字亦在大致相同时间出现;到了所谓“前萨尔贡时代”(公元前2600—前2340),则两河流域所特有的六十进制记数法以及在此基础上发展的四则运算法成熟,陶泥板上开始出现乘数表和除法问题,这后来就成为更高级的巴比伦数学之基础
 。
。
表1.4 混合六十进制记数法

六十进制记数法往往被国人视为笨拙、不切实际。当然,它的确及不上阿拉伯记数法和近世标准十进制算法的便捷,但却也并不如想象中那么复杂、困难。这有两个原因。首先,六十进制记数法所应用的基本数目字只是14个而并非60个,因为它是所谓“六十进与十进混合制”,因此,如表1.4所示,从1至59的任何一个数目都只要用1—9以及10、20、30、40、50这14个符号就可以表达。举例来说,中文的“三十七”以阿拉伯数字表示是“37”,在六十进制中仍然是“30”加“7”。其次,他们已经发明了全面的位置记数法,因此“五百八十九”以阿拉伯数字表示是589,在“混合六十进制”中可以分解为589=9×60+49,以现代六十进制记法可以简明地表示为[9,49];同样,更大的数目12736=3×60 2 +32×60+16,即[3,32,16],这以楔形符号表达也是同样方便的。
由于位置记数法的应用,这种六十进制记数法和我们熟悉的阿拉伯十进制记数法并没有根本差别:它可以轻松处理很大的数目,在其中加法和减法都很容易。乘法在原则上也和我们熟知的没有分别——只是60×60的乘数表不容易记住,必须求助于记载在陶泥板上的数表。至于除法,则的确不容易直接用心算,而需要借助于预先编制的“倒数表”,以将除数改变为乘数。不过,这计算系统虽然在多数情况下很方便、实际,但仍然有基本缺陷。首先,它尚没有相当于“0”的数字,因此无法准确表达诸如3601那样的数目——它应该是1×60 2 +1,即[1,0,1],所以必须用到“0”这个数字。其次,它没有小数点,所以数目的绝对值不能确定:上文的[9,49]既可以是589,也可以理解为589/60=9+49/60,甚或是589×60 n ,其中 n 是任意整数,正负均可。所以,在实际应用上,数目的绝对值只能根据问题的语境决定,这就严重地限制了它作为数学工具的独立性。最后,这计算系统中还没有普遍的分数观念;而且,对于像7,17,23这些不能够整除60的数目来说,“倒数表”只能给出近似而非准确结果,所以如何处理相关除数还是个大问题。
无论如何,位置记数所带来的巨大方便使得苏美尔的六十进制记数法和四则运算法流传下来,其符号和细节虽然有变更,但整体方法则为巴比伦和希腊数学家,包括像托勒密那样需要做大量繁复计算的天文学家所沿用。而且,上述缺陷也在后来逐渐得到弥补,这主要包括“0”符号以及六十进制小数点“;”的发明。今日十进制已经普及全世界,但由于历史上六十进制已经在天文、航海上广泛应用,所以它仍然遗留在方向、角度和时间的划分、记载上,即圆周分为360度,每度60分,每分60秒;每小时分为60分,每分60秒;等等。
其实,苏美尔数学并不完全止于四则运算。有清楚的证据显示,在霸主至萨尔贡时代(公元前2600—前2200),苏美尔陶泥板上已经出现解决测量亦即几何问题的一些基本方法,它们后来成为巴比伦时代解决更复杂同类问题的基础。为了方便,这些我们留待下面一并讨论。
巴比伦的数学陶泥板
两河流域数学的高峰在巴比伦旧王朝,但它并非缓慢地发展而来,其出现是相当突兀和独特的。如上文一再提到,出土的数学陶泥板绝大部分都属于此时期。而且这绝非偶然:虽然在它之前的乌尔第三王朝,和在它之后的卡塞特混乱时期和亚述帝国时期,都有大量陶泥板记录,其中却几乎没有任何数学文献,此后一直到公元前300年开始的塞琉西王朝,才重新有数学陶泥板出现。这个特殊现象是很令人惊讶的,它很可能和大规模文士教育体制(scribal institutions)的建立有密切关系,其意义下文还将讨论。
巴比伦数学陶泥板大致有三类:
(1)问题板,统共大约100块,这又可以再细分为两个次类:(a)解题板,每板只记录一至数题,数学问题本身和计算步骤都详细列出;(b)各种类型的问题集,其中有些类似于教科书中的练习题部分,但也有各种不同类型问题的集合,它们一般没有解法和答案,或者仅有答案而没有解法。
(2)数表,统共大约300块,这包括最简单和常用的乘数表、倒数表、度量衡转变表、平方和立方表,以及为解决更复杂问题而编制的特殊数表,例如复利表、高次方表、方根表、幂数表、平方与立方之和的数表等。
(3)少量计算板,也就是算草的记录。
显然,以上三者与我们今日所熟悉的教育文本大致对应:问题板类似于教科书,包括教材和习题两部分;数表类似于计算机出现以前常用的对数表和三角函数表;计算板则相当于学生的练习本或者算草纸。
四、巴比伦代数学
那么,在这个历时久远、规模庞大的巴比伦文士体系之中,数学的发展到底达到了什么程度呢?简单的答案是:他们最杰出的成就是解方程式,包括大量线性方程和一般二次方程的通解,这在西方本来以为要到欧几里得的《几何原本》才会出现。至于在中国,到西汉方才成书,历来被奉为圭臬的《九章算术》虽然有线性方程组解法,但二次方程解法只是在“勾股”章第二十问的所谓带“从法”的开方术简略提到,详细步骤则阙如。所以我们为将近四千年前的巴比伦代数学感到震惊是完全有道理的。除此之外,巴比伦数学还将数量关系应用到几何形体的划分上去,和利用数表得到高次方程式乃至超越方程式的近似解;对三角形、梯形、正多边形和圆形的边、周长和面积的研究,也是他们所长;不过立体的研究则似乎较少为他们注意。以下我们就上述最重要的几类问题举例说明
 。
。
二次方程式
二次方程解法是巴比伦数学的核心。当时还没有抽象的未知数概念,所以它的问题都是用正方形、长方形、面积、边长这些几何词汇和观念来建构,但我们可以判断,在底子里这些问题具有很强的抽象性质,这主要是因为在解决这些问题的运算中,经常会出现面积和长度相加减那样缺乏实际意义的情况。所以,将之称为“代数”是合理的。
现在我们举出编号为BM 13901的陶泥板所载第一题,来说明他们的基本解题方法,即通过“剪贴面积”来“完成平方”。以我们熟悉的语言表达,这个题目是:“[正方形的]面积加边长为 a ,求边长 x ”。倘若正方形的边长为 x ,其面积就是 x 2 ,因此这个问题相当于求解下列方程式: x 2 + x = a 。为了简便,以下我们用符号□( x )来代表“边长为 x 的正方形”之面积,用符号[ x , y ]来代表“边长为 x 和 y 的长方形”之面积。这样,陶泥板上的解法是(图1.2):
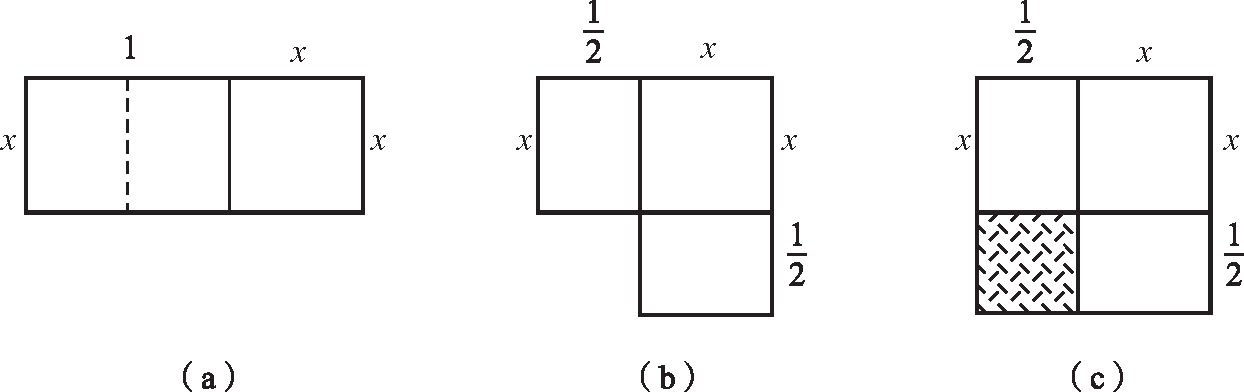
图1.2 以剪贴法解方程式 x 2 + x = a
(a)把长方形[1, x ](注意,这实际等于 x )附在正方形□( x )旁边,两者的总面积是 x 2 + x ;
(b)把长方形[1, x ]分割为两个长方形[1/2, x ],然后分别贴在正方形□( x )的两边,以造成一个曲尺形,但图形总面积维持不变,仍然是 x 2 + x ;
(c)把另一个面积为1/4的正方形□(1/2)贴附到曲尺形的内弯中,从而造成完整的正方形□( x +1/2),这样图形的总面积增加了1/4,即变成 a +1/4;
(d)于是,(
x
+1/2)
2
=
a
+1/4,也就解得
 。
。
显然,这解法和现代代数的“完成平方法”(completing the square)基本上一致,只不过前者是用面积的分割、挪动,也就是“剪贴”来“完成平方”,而不是用抽象符号达到目的而已。同板第二题有个简单变化,即求解 x 2 - x = a ,其方法和第一题基本相同,但需要从正方形“剪裁”掉(而非贴附上去)两个长方形面积。
同板第三题求解(2/3) x 2 +(1/3) x = a ,即具任意系数的二次方程式,解法相当于将 ax 2 + bx = c 全部乘以 a ,从而得到( ax ) 2 + b ( ax )= ac ;然后令 y = ax ,将方程式变为 y 2 + by = ac 的形式,最后完成平方。在图1.3中,这相当于把面积为 a 的长方形[ x ,(2/3) x +(1/3)]的一边减少1/3,造成长方形[(2/3) x ,(2/3) x +(1/3)],其面积为(2/3) a 。这已经具有第一题“未知正方形加有相同边之长方形”即 y ( y + b )的形式, y =(2/3) x ,所以可以立刻用“完成平方”的办法求解。换而言之,这是在“完成平方”这个基本方法以外加上“变换未知数尺度”的方法,这可以说是二次方程解法的两个基本原则。
图1.3 以剪贴法解方程式(2/3) x 2 +(1/3) x = a
基本相同策略也同样可以解决二次型的二元方程式。例如, xy = a , x-y = b 这样的联立方程式(陶泥板YBC 6967)就很容易通过前述面积变形和剪贴的方式解决,而另外一道关于买卖的问题(TMS XIII)实际上相当于同样的方程式,并且是以相同的面积变换方法解决的。当然,可以归入二次方程式类的还有很多问题,解决方法也变化多端,例如有所谓“假设法”(false position),那就是变换未知数;有些问题导致“双二次型方程”(biquadratic equation),即 ax 2 n + bx n = c (其中 n =2,3,4,…),那显然也可以用前述标准办法解决。例如陶泥板TMS XIX上的第二题就属于 n =4型,其中牵涉以某正立方体体积为“边长”的长方形。这显示出当时文士对于他们所发展的“代数”的运算能力产生了好奇,因此有兴趣探究它的极限。
求平方根
陶泥板上有多种求平方根的方法,但都是作为解决问题的实际手段,而并没有系统的程序。例如,他们会应用下列近似公式(VAT 6598#6):
 ,这和应用二次展开式所得到的最低近似公式吻合。虽然文献中没有显示如何得到这种算法,但上述“完成平方”的基本手段可以很轻易地应用在此问题上。例如,问题可以视为要将大小不同的两个正方形□(
a
)和□(
b
)变为一个正方形(图1.4),步骤如下:
,这和应用二次展开式所得到的最低近似公式吻合。虽然文献中没有显示如何得到这种算法,但上述“完成平方”的基本手段可以很轻易地应用在此问题上。例如,问题可以视为要将大小不同的两个正方形□(
a
)和□(
b
)变为一个正方形(图1.4),步骤如下:
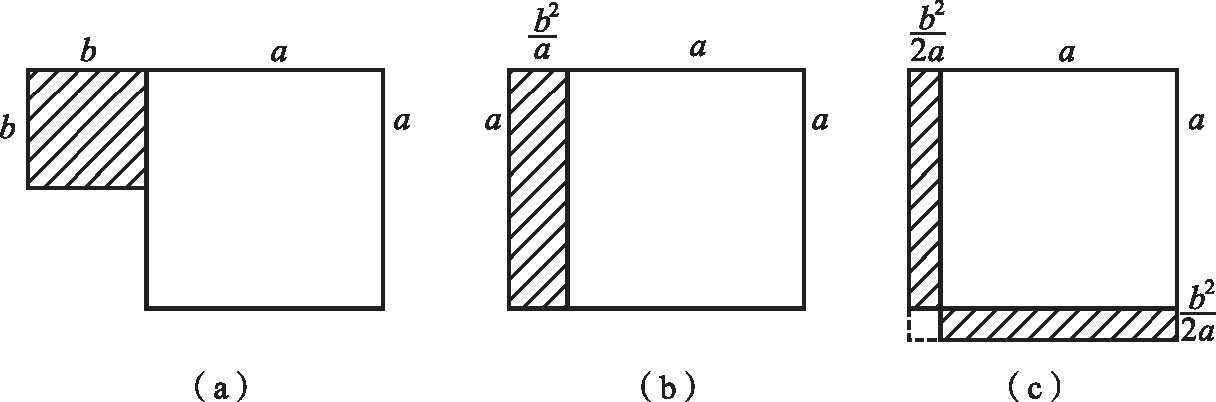
图1.4 以剪贴法求

(1)把正方形□( b )转变为等面积的长方形[ a , b 2 / a ]贴附在□( a )旁边;
(2)把[ a , b 2 / a ]分拆成两个长方形[ a , b 2 /2 a ],分别贴附到□( a )的两边;
(3)这样造成的曲尺形的内凹部分较小,可以忽略,因此它可以视为正方形□( a + b 2 /2 a ),那么原面积的开方就大约是 a + b 2 /2 a 了。
显然,这近似解法在a>>b时最有效。在上述陶泥板问题中
a
=40,
b
=10,近似结果可以准确到0.04%。此外,倘若问题是求任意数
A
的平方根,那么显然可以先估计一个(较小的)近似尝试值
a
,然后采取与上述相同的步骤得到更准确的修正值
a
1
=
a
+
b
2
/2
a
,其中显然
b
2
=
A-a
2
,亦即
a
1
=(
a
+
A/a
)/2。这是个非常简便,也很容易反复代入求高次修正值的公式。例如,以1作为
 的尝试值
a
(即
A
=2),那么反复代入所得近似值依次是:
a
1
=1.5,
a
2
=1.416,
a
3
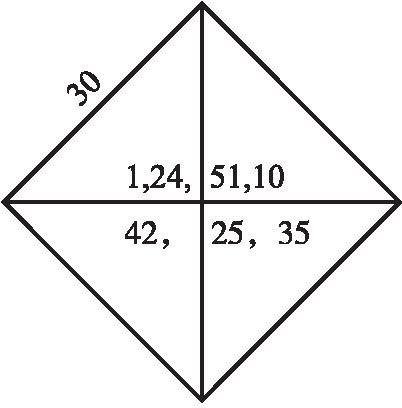
=1.4142157,那已经准确到百万分之1.5了。虽然陶泥板上并没有这计算法的直接记录,但像奈格包尔等专家都认为,这有绝大可能是他们实际的运算方法。证据是:陶泥板YBC 7289上没有文字,它所显示的如下图(
并见图版2
),是个带对角线的正方形,上面注明了边长(30)和对角线长([42,25,35],即42.426389),以及[1,24,51,10],那相当于十进制的1.414213,这正好是所注明的对角线长和边长之比,所以毫无疑问,正是他们的
的尝试值
a
(即
A
=2),那么反复代入所得近似值依次是:
a
1
=1.5,
a
2
=1.416,
a
3
=1.4142157,那已经准确到百万分之1.5了。虽然陶泥板上并没有这计算法的直接记录,但像奈格包尔等专家都认为,这有绝大可能是他们实际的运算方法。证据是:陶泥板YBC 7289上没有文字,它所显示的如下图(
并见图版2
),是个带对角线的正方形,上面注明了边长(30)和对角线长([42,25,35],即42.426389),以及[1,24,51,10],那相当于十进制的1.414213,这正好是所注明的对角线长和边长之比,所以毫无疑问,正是他们的
 近似值,而它和上述第三修正值
a
3
是基本相同的。
近似值,而它和上述第三修正值
a
3
是基本相同的。
三次方程式
巴比伦文士在二次方程式和二次根问题上成绩斐然,这大体上已经达到他们系统运算能力的限度了。他们留下了一些企图解决更高次问题的记录,但显然并没有获得突破。例如陶泥板YBC 6295是开立方问题,也就是从正立方体的体积求边长,但解法却是“找到”适当的“参考正立方体”,它的体积“恰好”是所给体积的1/27,因此所求边长是“参考正立方体”边长的3倍,如此而已。此外陶泥板BM 85200+VAT 6599长达156行,有30道题目,这些都和挖掘泥土有关,并且导致一些“不齐次型”(inhomogeneous)三次方程式,但他们同样无法提出普遍解法——这得到三千多年后,即公元16世纪才会有突破。
另一方面,陶泥板上也列出 n 3 + n 2 ( n =1,2,3,…,30)数值的数表,这可以视为解决不齐三次方程 x 3 + x 2 = a 的重要准备工作,而且板上的确有从数表反求变量的解法记录;至于更普遍的方程 ax 3 + bx 2 = c ,自然也可以通过他们所熟悉的“重标度”(re-scaling)变量转换而化约成前面的标准式。这方面的工作应当视为巴比伦数学在解三次方程的最成功尝试。除此之外,应当顺带提到,陶泥板上还有幂数表 a n ( n =2,3,4,…)以及反求幂数的问题,虽然语焉不详,也可以视为探索对数(logarithm)关系的滥觞。
不过,巴比伦文士显然还未曾发展出负数观念,更没有意识到二次方程式可以有两个解。也就是说,他们在陶泥板上所解决的大量二次方程问题虽然已经脱离实际需要,而变为在专业训练中发展出来的智力考验或者游戏,然而在观念和方法上,还没有彻底抽象化和系统化。因此这只能够说是代数的雏形,它与严格意义的现代数学之间还有很大距离。
五、代数型几何学
除了“几何化”的代数以外,陶泥板上有不少真正的几何问题,但是它们的基本关怀仍然是简单直线图形的数量关系,而并非线条的空间关系,或者几何形体的度量。所以,称之为代数型的几何学是很恰当的。
几何形体度量
整体而言,巴比伦数学对几何形体的直接度量并没有什么令人惊讶的发现。在奈格包尔和萨赫斯合编的《楔形文字数学文献》与此相关的部分有十余块陶泥板,上面载有超过百道算题
 ,其性质都是和挖土、砌砖、疏浚运河等实际问题有关,所牵涉的数学只限于简单比例和立方体、圆柱体体积的计算而已。唯一的例外,是出现在陶泥板YBC 5037的35—44题中的下列正截锥体体积近似公式:
V
=
h
(
a
2
+
b
2
)/2,其中
h
,
a
,
b
分别是其高度和上下两面的边长:显然,比之莫斯科数学手卷的发现,它是差得远了。
,其性质都是和挖土、砌砖、疏浚运河等实际问题有关,所牵涉的数学只限于简单比例和立方体、圆柱体体积的计算而已。唯一的例外,是出现在陶泥板YBC 5037的35—44题中的下列正截锥体体积近似公式:
V
=
h
(
a
2
+
b
2
)/2,其中
h
,
a
,
b
分别是其高度和上下两面的边长:显然,比之莫斯科数学手卷的发现,它是差得远了。
在多数陶泥板上,圆周率一般只用极其粗略的3,这未免令人惊讶。但在苏萨(Susa)出土的文献却证明他们对此有更仔细的研究,因为其列出了正多边形面积
A
n
与边长
a
n
的关系:
 ;
;
 ;等等。由于我们知道,
A
3
和
;等等。由于我们知道,
A
3
和
 的比值应该是
的比值应该是
 ,因此可以推断在巴比伦数学中,
,因此可以推断在巴比伦数学中,
 ,这大约准确至1%。此外,在同一文献中,还有正六边形周长
C
6
与外接圆周长
C
的关系:
C
6
=(24/25)
C
。由于
C
6
=3
C
/π,这相当于π=25/8,那准确到0.5%,和埃及数学所得不相上下。然而,他们到底从何得到24/25的比例,是不清楚的。值得注意的是:在
n
=5,6,7时,上列
A
n
公式和公元1世纪希腊数学家赫伦在他的《测量学》(
Metrica
)中所列出的(见§6.2)并无二致。因此,他所承袭的,很可能是巴比伦而并非希腊本身的传统
,这大约准确至1%。此外,在同一文献中,还有正六边形周长
C
6
与外接圆周长
C
的关系:
C
6
=(24/25)
C
。由于
C
6
=3
C
/π,这相当于π=25/8,那准确到0.5%,和埃及数学所得不相上下。然而,他们到底从何得到24/25的比例,是不清楚的。值得注意的是:在
n
=5,6,7时,上列
A
n
公式和公元1世纪希腊数学家赫伦在他的《测量学》(
Metrica
)中所列出的(见§6.2)并无二致。因此,他所承袭的,很可能是巴比伦而并非希腊本身的传统
 。
。
平面形的分割
陶泥板上真正深入探讨的几何问题,其实还是离不开代数计算,而这是有深厚基础的,因为在公元前2200年的苏美尔陶泥板上,已经有几何图形划分的记载。这基本上有两项。首先,是相当于(
R-r
)
2
展开式的面积关系□(
R-r
)+2[
R
,
r
]=□(
R
)+□(
r
)。这关系很容易在图1.5中看出来,因为显然
A
=□(
R-r
),
B
=□(
r
),
C
=[
R
,
r
]-
B
,□(
R
)=
A
+
B
+2
C
=
A-B
+2[
R
,
r
]。其次,如图1.6所示,倘若要以平行线
EF
平均分割正梯形
ABCD
,那么梯形
AEFB
=[□(
a
)-□(
c
)]/4=梯形
EFCD
=[□(
c
)-□(
b
)]/4,因此立刻得到□(
c
)=[□(
a
)+□(
b
)]/2,这就是巴比伦数学中常用的“分割边的平方等于两平行边平方的平均数”定理
 。
。
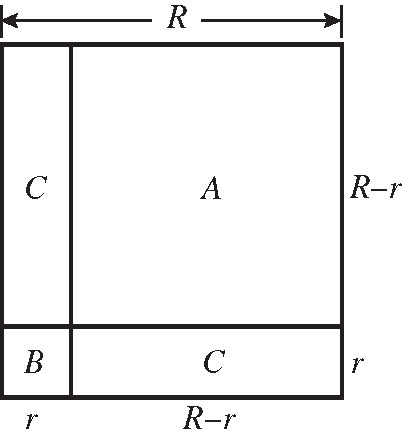
图1.5 以图解显示二次展开式□( R-r )+2[ R , r ]=□( R )+□( r )
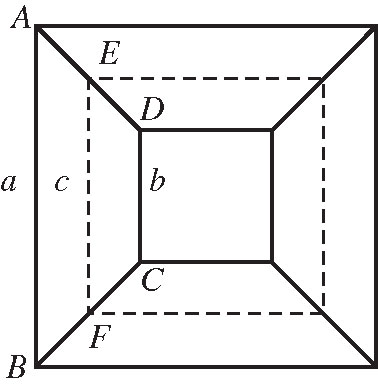
图1.6 以平行线 EF 等分正梯形 ABCD 之面积
在旧巴比伦王朝时代各种几何图形分割的问题广受热爱,而解法基本上都是以上述两个发现或曰“定理”为基础。以下我们举陶泥板VAT 8512上的突出例子说明这定理的应用
 。这是一道相当困难的三角形不等划分问题,它不但解法十分巧妙,而且充分显示了巴比伦数学运用平分梯形以及转变标度的纯熟技巧。题目是:以平行虚线将直角三角形划分为不等的两半,以使分割后的边长差为
q
=
b-a
,面积差为
S
=
A-B
;从
q
,
S
和三角形的边长
h
,求分割线长
x
,分割后的边长
a
,
b
,以及分割后的面积
A
,
B
(图1.7a)。
。这是一道相当困难的三角形不等划分问题,它不但解法十分巧妙,而且充分显示了巴比伦数学运用平分梯形以及转变标度的纯熟技巧。题目是:以平行虚线将直角三角形划分为不等的两半,以使分割后的边长差为
q
=
b-a
,面积差为
S
=
A-B
;从
q
,
S
和三角形的边长
h
,求分割线长
x
,分割后的边长
a
,
b
,以及分割后的面积
A
,
B
(图1.7a)。
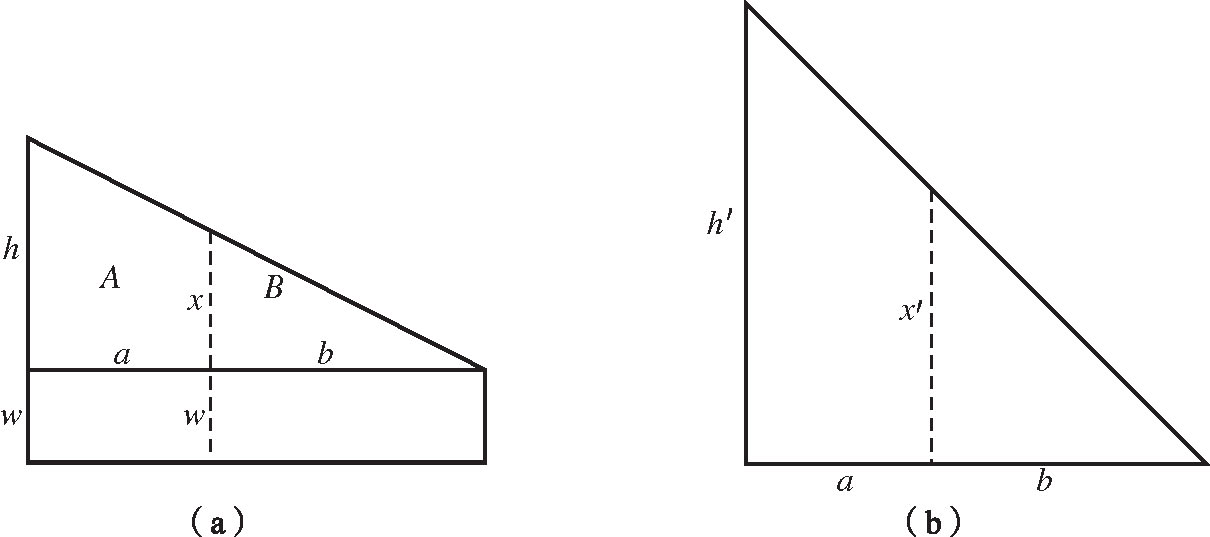
图1.7 将直角三角形面积作不等分配问题的图解
解法是:在三角形下面附加一个宽度为 w 的长方形,以令两者合并构成一个梯形,并且要求分割线(及其延长)平分这梯形:
A + wa = B + wb ,即 w =( A-B )/( b-a )= S/q
因此长方形宽度 w 可以简单决定。但梯形既然是平分了,那么也就可以用上述有关定理:
□( x + w )=[□( h + w )+□( w )]/2
由之可以简单地算出 x + w 并从而决定 x 。
但求得 x 之后,还得求边长 a , b 和面积 A , B 。为此,板上列出的解法也是颇富于创造性和巧思的(图1.7b):改变宽度 h 的标度(scale)以使三角形成为等边,即令 Ph = a + b ,这样同时还可以得到 Px = b ,以及 P ( A + B )=□( a + b )/2, PB =□( b )/2,因此
P ( A-B )= PS =[□( a + b )-2□( b )]/2=□( P )[□( h )-2□( x )]/2,这就求得了标度因子 P :
P =2 S /[□( h )-2□( x )]
由之就可以直接算出 b , a 和 A , B 。倘若试图循现代一般方式解此问题,则需解一具有五个未知数并带二次项的联立方程式,由是可深知上法之巧妙。
毕达哥拉斯定理
数学陶泥板上只有计算的步骤,而很少解释,更没有论述,所以我们并没有巴比伦文士是否具有几何观念的直接证据。然而,从他们所遗留关于正方形、长方形、梯形的大量计算以及相关图解看来,他们肯定并不缺乏关于“垂直”和“平行”的观念——虽然这不一定很抽象或者严格。而且,他们也显然知道并经常利用毕达哥拉斯定理——这并不奇怪,因为这个定理和他们所感兴趣的计算关系非常密切,在多达9块陶泥板上的各种计算都可以强有力地证明这一点
 。
。
不但如此,奈格包尔在详细研究著名的Plimpton 322号陶泥板( 图版3 )数表之后认为,撰作此板的文士很可能还知道“毕达哥拉斯数组”的标准生成法。此法如下:令 b , c , d 数组适合毕氏方程式 d 2 = b 2 + c 2 ,也就是说,它是“毕氏数组”,那么它可以从一任何整数对 p , q ( p > q )产生,只要令
b = p 2 - q 2 , c =2 pq , d = p 2 + q 2
即可,因为对任何
p
,
q
来说,前述的毕氏方程恒真。前述Plimpton数表共有4列,15行,所列出的除了各行顺序数
[1]
以外,是(
d/c
)
2
,
b
,
d
这三列数,其中
d
,
b
,
c
是上述毕氏数组。奈格包尔所发现的是:表中的
c
全部可以整除
d
;由于
d/c
=(
p/q
+
q/p
)/2,这整除的要求意味着在六十进制中
p
和
q
的倒数都必须是有限数,而事实上,与表中各行对应的
p
,
q
值也的确全部是在陶泥板标准倒数表中出现的
 。
。
最后,甚至有迹象显示,巴比伦文士可能已经知道“何以”勾股定理是对的——虽然我们并没有证据表明他们曾经发展出“证明”的观念。这些迹象主要系于曾经多次出现的,由四个相同长方形首尾回环连接而构成的一个正方形(图1.8)
 。与此图相关的问题(陶泥板DB
2
-146)是:从长方形的面积[
a
,
b
]和对角线长
c
求边长
a
,
b
。它的解法意义不是很清楚,但最后是用了勾股定理,而且牵涉诸如□(
a
+
b
)和□(
a-b
)这些面积。而从图1.8可以见到,只要考虑由四个长方形的对角线
c
所形成的正方形,那么无论用下面哪一个关系:
。与此图相关的问题(陶泥板DB
2
-146)是:从长方形的面积[
a
,
b
]和对角线长
c
求边长
a
,
b
。它的解法意义不是很清楚,但最后是用了勾股定理,而且牵涉诸如□(
a
+
b
)和□(
a-b
)这些面积。而从图1.8可以见到,只要考虑由四个长方形的对角线
c
所形成的正方形,那么无论用下面哪一个关系:
□( c )=□( a + b )-4[ a , b ]/2(即最外正方形减去四角)
□( c )=4[ a , b ]/2+□( b-a )(即四角加上中间的小正方形)
都可以立刻得到勾股定理□(
c
)=□(
a
)+□(
b
)。所以,目前已经出土的文献虽然还不足以支持勾股定理在当时已经得到证明的说法,但综合以上各种证据,说当时对于勾股定理已经有很深刻认识甚至证明意识,那大概是不错的。值得注意的是,图1.8和《周髀算经》中用以证明“勾股定理”亦即毕达哥拉斯定理的“赵爽弦图”基本相同,但两者之间是否有关系就很难说了
 。
。
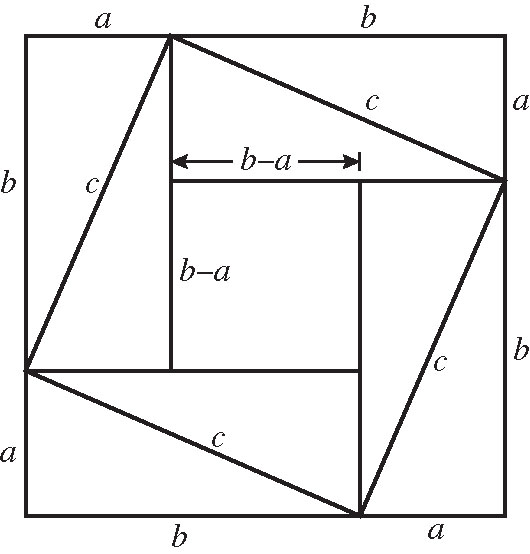
图1.8 用以证明毕达哥拉斯定理的“环矩图”
远古数学的启示
那么,具有将近四千年历史的两河流域数学除了令人对它的精妙、久远感到震惊以外,到底还告诉了我们些什么呢?首先,它令我们意识到,数学发展不一定稳定和依循直线,更未必是由实用价值所推动。苏美尔文明遗留在数学陶泥板上的第一阶段数学是缓慢、稳定发展,由实用需求所带动的。这是个历时千年以上的过程:最初出现的是实物记录,它逐步演变为符号、数字,乃至以位置记数法表示的数目,最后四则运算和数表出现。在此阶段数学始终没有超越实用目标,它的内容仅限于具有直接日常应用意义的四则和比例算题。然而,巴比伦文明所显示的第二阶段发展却完全不同:在实用类型问题的延续之外,数学陶泥板上涌现了大量性质上明显属于“超实用”,并且表现出相当高技巧的问题。但这并不能够持续:在随后的卡塞特混乱时期和亚述帝国时期,数学就完全沉寂下来,只有凤毛麟角的一两块数学陶泥板留存;这样一直要到塞琉西时期,才再有数学陶泥板出现。
所以,数学虽然起源于实用,但它的进一步发展也就是“突破”却似乎有赖于“超实用”(supra-utilitarian)的兴趣与动机,也就是纯粹为了好奇或者炫耀而作的探究,以及容许,甚至鼓励这种探究的环境。这种发展带有“突变”甚至“革命”性质,而且它是不稳定的,极可能由于政治、社会、文化环境的改变而受到挫折,甚至消失。海鲁普认为,数学的突破性发展之出现于旧巴比伦王朝,很可能是因为它大规模发展了气氛宽松、带有人文气息和自主性的文士学堂(scribal school)。这些学堂提供了具有普遍意义的教育,即所谓博雅教育,而不仅仅是狭隘的技术、职业训练。由是相应的专业教师阶层得以兴起,为数学脱离直接实用需求,在小部分“专家”当中向精巧美妙的方向发展提供了土壤;同时教材的需求大增——我们今日看到的陶泥板数学文献,大部分就是由此而来。数学要能够发展到相当复杂的程度,并且变为一门独立学问,似乎必须倚靠这种土壤——一个既有闲暇也有高度专业兴趣和自豪感的阶层之形成。而这种体制和相应阶层之消失,可能也就是数学突然中衰的原因
 。
。
六、希腊文明的渊源
巴比伦数学充分显示,西方数学有着极其深厚的渊源,其年代之悠久远远超过以往想象——事实上,它的萌芽是和西方文明本身同步的。当然,这个认识凸显了另外一个问题,那就是:古希腊数学与巴比伦数学之间究竟有何关系?西方数学大传统的确可以一直追溯到巴比伦乃至苏美尔文明吗?这不是个容易回答的问题,它牵涉希腊文明与两河流域文明之间的整体关系,因而不免受制于某些学者所固执的观点,从而引起难解争论。不过,在最近二三十年,由于在中东不断出现新证据,这种情况已经逐渐改变,希腊文明在多方面受到中东影响这一点,已不容否认,两者之间的传承关系,也慢慢为学界所接受了。
在以往不少学者的印象中,巴比伦和亚述帝国是崇尚武力与君主意志、视民众如草芥的高度集权国家;古埃及则是尼罗河、金字塔和法老王的世界,在彼庞大官僚机构统治百千万黎民,驱使他们夜以继日地开凿、搬运沉重石块,为统治者建造不可思议的巨大陵墓,在他们死后把保存完好的木乃伊躯体封闭其中,让其安静等待未来的复活。这样忽视个人价值的国度,竟然是追求公平、理性和抽象思维的希腊文明之源头,简直不可思议。然而,古希腊人自己却认为,他们的文化包括数学、哲学是承受于埃及、巴比伦(这指的自然是公元前7—前6世纪之间的“迦勒底巴比伦帝国”)、波斯这些远古文明。他们最早的哲人泰勒斯和毕达哥拉斯相传都到过埃及和巴比伦,并且曾经长时期在那里的神庙跟随祭司学习。他们的“历史之父”希罗多德(Herodotus)猜测,几何学本来是埃及人为了每年尼罗河泛滥之后重新丈量土地而发明的。柏拉图在《对话录》中也一再借埃及祭司的口吻,提到他们悠久的传统和深不可测的累积智慧,在其面前希腊哲人只不过像是孩童。整体而言,在古代希腊人观念中,东方的远古文明是博大精深、不可忽视的,他们自己的成就虽然值得自豪,但不可能凭空而生,其源头必然和远古文明有关。当然,上述传闻、猜测并无具体细节,《对话录》也颇不乏寓言、夸张和想象之词,所以在缺乏有力旁证的情况下,许多前代学者认为,那都只不过是古希腊人震惊于这些文明之久远而生出的想当然说法,不足深信。然而,传世古史为后来出土资料所证实的例子在近代考古学中屡见不鲜,我们现在也不可能对这些根深蒂固的传闻采取一概抹杀的态度了。
希腊主义的退潮
事实上,希腊文明整体(而不仅仅是其科学)与远古文明的关系在六十年前就已经受到西方学界关注了。当时考古学家戈登(Cyrus H. Gordon)在其《希腊与希伯来文明的共同背景》一书中提出这样肯定的观点:“在诸如乌格列的考古发现令我们不再能够将希腊视为密封的奥林匹克奇迹,或者将以色列视为真空包装的西奈半岛神迹……希腊与希伯来文明都是建立在东地中海同一基础上的平行结构。”
 他的观点基本上是由叙利亚海岸古遗址乌格列(Ugarit)之发现而触发,但论据则建立在许多有相同结构的史诗、故事之比较上,例如希腊的《奥德赛》(
Odyssey
)与苏美尔的《基格米殊》,希腊的《伊利亚特》(
Iliad
)与乌格列的《克勒特》(
The Epic of Kret
),希伯来的《出埃及记》与埃及中王朝时代的民间故事《辛努赫》(
The Tale of Sinuhe
),等等。在此后十年,这种观点从文学扩展到哲学:牛津的古典学家韦斯特(Martin L. West)研究希腊最早期哲学与东方的关系时得到了这样的结论:“公元前550—前480年是伊朗积极影响希腊思想发展的一个突出时期。”他所说的,正是阿那克西曼德(Anaximander)、阿那克西米尼(Anaximenes)、毕达哥拉斯(Pythagoras)、赫拉克利特(Heraclitus)、巴门尼德(Parmenides)这些“前苏格拉底”自然哲学家的开创时代。他认为,波斯居鲁士(Cyrus)大帝吞并米堤亚(Mede)王国,可能就是引致该地称为“马古斯”(Magus)的哲人大批移居小亚细亚西岸,从而刺激希腊哲学兴起的原因
他的观点基本上是由叙利亚海岸古遗址乌格列(Ugarit)之发现而触发,但论据则建立在许多有相同结构的史诗、故事之比较上,例如希腊的《奥德赛》(
Odyssey
)与苏美尔的《基格米殊》,希腊的《伊利亚特》(
Iliad
)与乌格列的《克勒特》(
The Epic of Kret
),希伯来的《出埃及记》与埃及中王朝时代的民间故事《辛努赫》(
The Tale of Sinuhe
),等等。在此后十年,这种观点从文学扩展到哲学:牛津的古典学家韦斯特(Martin L. West)研究希腊最早期哲学与东方的关系时得到了这样的结论:“公元前550—前480年是伊朗积极影响希腊思想发展的一个突出时期。”他所说的,正是阿那克西曼德(Anaximander)、阿那克西米尼(Anaximenes)、毕达哥拉斯(Pythagoras)、赫拉克利特(Heraclitus)、巴门尼德(Parmenides)这些“前苏格拉底”自然哲学家的开创时代。他认为,波斯居鲁士(Cyrus)大帝吞并米堤亚(Mede)王国,可能就是引致该地称为“马古斯”(Magus)的哲人大批移居小亚细亚西岸,从而刺激希腊哲学兴起的原因
 。
。
但是,即使到了20世纪90年代,对于这些观点仍然不是没有抗拒的。持开放观点的德国学者布尔克特(Walter Burkert)在《东方化革命:近东对希腊文化在古代早期的影响》一书中就说得很感慨,也很坦白:“……即使在今日,要持平地讨论古典希腊与东方的关系还是困难,谁要作此尝试就会碰到不可动摇的观点、不安、辩护,乃至忿恨。谨慎的防卫心态将陌生与未知事物拒诸门外。在很大程度上,这是开始于两个多世纪之前,而主要生根于德国的思潮之结果。”不过,正如他跟着所指出的那样,自20世纪中叶以来,这一度声势浩大的“希腊主义”(Hellenism)已经在大量证据面前逐渐退潮。希腊文明之在许多方面受到两河流域和其他中东文明的深刻影响,已经是不争的事实了。他自己的著作引用了大量古希腊与中东有关其史诗、神话的考古发现,以将两者联系起来,其中最引人注目的,包括中东的可怕女怪拉马什图(Lamashtu)与希腊的蛇发女怪戈耳工(Gorgon)之相似;以及希腊英雄珀耳修斯(Perseus)在雅典娜帮助下杀死戈耳工的铜刻画像,与基格米殊杀死怪物洪巴巴(Humbaba)的中东圆柱形陶泥印章之如出一辙,等等
 。但是,戈登与布尔克特所搜集的证据虽然广泛,真正深入而细致的考究则有赖韦斯特继其70年代工作之后,于20世纪末出版的巨著《赫利孔山的东面:希腊诗歌与神话中的西亚素材》
。但是,戈登与布尔克特所搜集的证据虽然广泛,真正深入而细致的考究则有赖韦斯特继其70年代工作之后,于20世纪末出版的巨著《赫利孔山的东面:希腊诗歌与神话中的西亚素材》
 。以下我们就此书所讨论的问题以及相关历史与宗教背景稍微再作一点说明。
。以下我们就此书所讨论的问题以及相关历史与宗教背景稍微再作一点说明。
赫利孔山的东面
希腊的信史大致从首届奥林匹克竞技会(公元前776)开始,可是,毫无疑问,希腊文化上第一件大事是荷马(Homer)史诗的出现。它的确切年代已经不可考,希罗多德认为是在自己之前四百年,即公元前850年左右,这个估计是大家历来接受的。在此之前,最具有决定性,最能够熔铸希腊意识的事件,就是作为荷马史诗《伊利亚特》主题的特洛伊(Troy)战争。此长篇诗歌所记载的希腊联军远征特洛伊的故事历来被视为神话、传说,但我们现在知道,它虽然有不少想象和编造成分,但叙事框架和许多细节却并非向壁虚构,而的确可以通过考古和文献研究找到根据。特别是,经过20世纪多次田野发掘,考古学家发现了在小亚细亚西北近达达尼尔(Dardarnelles)海峡入口处的特洛伊多层遗址。它是控制欧亚之间以及地中海与黑海之间贸易的交通枢纽,历史极其悠久,在公元前3000—前1300年一共经过六个时期的累积,至于第七期(Troy ⅦA,公元前1300—前1200)则是个非常富裕和强大的政治、军事和贸易体系的中心。此城在公元前1200年左右被焚毁,其后完全衰落。因此它所反映的,应当就是《伊利亚特》所描述的战争,亦即希腊构成民族三支之一的亚该亚人(Achaean)联军渡海征服特洛伊这希腊史上的大事 [2] 。
荷马在世大约是公元前850至前750年之间,比特洛伊战争只晚三四百年。他是爱奥尼亚海岸希俄斯岛(Chios)人——或者,应该说,他的后裔族人称为“Homeridae”者在该岛繁衍,那里北离特洛伊160公里,南离自然哲学发源地米利都(Miletus)、萨摩斯(Samos)只百余公里
 。他的史诗不但为当时的历史、社会留下重要见证,并且在两方面塑造了希腊文明。其一,是熔铸希腊的民族意识;其二,更重要的,是塑造了希腊早期的朴素宗教观,在其中奥林匹克山上的众多神祇在感情、私欲、行事作为上与凡人一般无异;神与人之分别,只在于前者能力极其强大,而且长生不老,这两点为凡人所绝对无法企及——正如一般民众不能企及阿伽门农王(Agammemnon)或者其他部族首领的体能和权力一样。色诺芬(Xenophanes)说得好:“从头开始,人人都是从荷马那里学来的。”
。他的史诗不但为当时的历史、社会留下重要见证,并且在两方面塑造了希腊文明。其一,是熔铸希腊的民族意识;其二,更重要的,是塑造了希腊早期的朴素宗教观,在其中奥林匹克山上的众多神祇在感情、私欲、行事作为上与凡人一般无异;神与人之分别,只在于前者能力极其强大,而且长生不老,这两点为凡人所绝对无法企及——正如一般民众不能企及阿伽门农王(Agammemnon)或者其他部族首领的体能和权力一样。色诺芬(Xenophanes)说得好:“从头开始,人人都是从荷马那里学来的。”

然而,《伊利亚特》是完全出于原创的观念,现在已经被打破了。在戈登和布尔克特工作的基础上,韦斯特更进一步,在《赫利孔山的东面》一书中以大量文献比较和研究证明:荷马的伟大创作并非凭空而来,它有无可置疑的东方渊源。那也就是说,《伊利亚特》的布局、情节、描述笔触,甚至它的主角,具有悲剧命运的大英雄阿喀琉斯(Achilles),都并非纯粹凭当地的传说和个人想象创造出来,而是有所本的。所有这一切的本源,就是在苏美尔文明中出现,而后在中东广为传播的《基格米殊史诗》(
The Gilgemesh Epic
)
 。事实上,大英雄基格米殊正是《伊利亚特》悲剧性主角阿喀琉斯的原型。这个长久以来为西方学者忽略的关联,现在已经由于大量陶泥板文献的出土与解读,以及少数学者锲而不舍的长期钻研得以证实。根据布尔克特、韦斯特与其他学者的考据,荷马的另外一部史诗《奥德赛》,以及其他早期希腊文学,诸如与荷马大致同时的赫西奥德(Hesiod)的《神统纪》(
Theogony
)和《工作与时日》(
Works and Days
),以及公元前5世纪悲剧作家埃斯库罗斯(Aeschylus)的作品,乃至希腊早期的宗教观念等,也莫不深受近东影响
。事实上,大英雄基格米殊正是《伊利亚特》悲剧性主角阿喀琉斯的原型。这个长久以来为西方学者忽略的关联,现在已经由于大量陶泥板文献的出土与解读,以及少数学者锲而不舍的长期钻研得以证实。根据布尔克特、韦斯特与其他学者的考据,荷马的另外一部史诗《奥德赛》,以及其他早期希腊文学,诸如与荷马大致同时的赫西奥德(Hesiod)的《神统纪》(
Theogony
)和《工作与时日》(
Works and Days
),以及公元前5世纪悲剧作家埃斯库罗斯(Aeschylus)的作品,乃至希腊早期的宗教观念等,也莫不深受近东影响
 。韦斯特在他的书题中特别提醒我们,希腊众文艺女神缪斯(Muses)所居的赫利孔山(Helicon)有其向东的一面,就是此意。
。韦斯特在他的书题中特别提醒我们,希腊众文艺女神缪斯(Muses)所居的赫利孔山(Helicon)有其向东的一面,就是此意。
东方文明西传的途径
但东方的神话、史诗,是如何西传的呢?根据韦斯特的论证,这开始于新亚述帝国于公元前934年兴起:它的军队在半个世纪后到达巴勒斯坦海岸,随后一再入侵腓尼基(Phoenicia)和小亚细亚东南的西利西亚(Celicia)海岸。因此,在迈锡尼文明覆灭和古典希腊文明形成的最初阶段(§2.1),两河流域文明势力同时到达已经希腊化的塞浦路斯岛东面和北面海岸,为东方文明的西传打下了基础。但真正关键性的转变则可能来自提革拉帕拉萨三世(Tiglath-Pileser Ⅲ,公元前744—前727年在位)所推行的大规模民众迁徙政策,即将所征服地的民众迁徙到两河流域,同时将大量亚述、巴比伦民众迁徙到腓尼基、西利西亚。从这时候开始,亚述帝国与塞浦路斯希腊政权的军事冲突以及政治交涉也开始有明文记载了。总的来说,从公元前9世纪开始,东方文明往西传播到希腊的途径就已经具备,其枢纽极可能是乌格列和塞浦路斯
 。
。
当然,即使有了政治和经济接触,抽象的文化内容诸如宗教信仰、文学著作、科学观念等到底以什么方式传播,也还是一个不容易回答的问题——由于阿卡德语和楔形文字从未在爱琴海世界流行,这个问题更为突出。在这方面有许多猜测,其中可能性最大的,是通过贸易、婚姻、谋生、逃难、应聘、流浪、寻找工作等各种原因而产生的人口流动。在当时海上交通已经十分普遍,而对人口的控制则远不如近代,因此这种流动是相当自由和广泛的。经常为学者引用以说明这流动之普遍的,是《奥德赛》里面奥德修斯(Odysseus)的老仆人尤美乌斯(Eumaeus)所说的:“谁会跑到别处去请回来一个陌生人呢?除非[请的]是对大家都有用的人,像占卜的、治病的、做木工的,甚至能够演唱取悦的歌者吧?这些是在无垠大地上往来,而会受到邀请的人。” [3]
科学文献上的证据
因此,自公元前9世纪以来,希腊与埃及、巴勒斯坦、两河流域、波斯这些东方文明并不是分离、孤立的,而是在艺术、器物、文学、宗教等各方面都有交流,都受其影响。在此大背景下,旧巴比伦数学依循相类似途径和方式渗透、传播到爱奥尼亚,从而影响希腊数学发展的可能性是难以排除的。例如,迟至公元前3世纪,仍然有巴比伦祭司迁徙到小亚细亚西海岸,并且开设学校教授天文学的事实(§4.5)。但是,除了希腊早期哲人曾经在东方游历的多处记载以外,这种可能性还有什么其他更为直接的证据呢?必须承认,相对于文学、宗教、民俗等各方面而言,能够显示这些文明之间在科学上也有传承关系的资料并不多。这巨大差别可能反映了希腊文明在科学上的创新能力,但恐怕也有一部分是由于科学领域的性质不同,即它只关乎极少数精英分子的活动,因此遗留下来的传承痕迹十分稀少。
不过,虽然如此,仍然有例外。那就是在欧几里得的经典《几何原本》第六卷之中,有许多公式事实上与其前一千三百多年在巴比伦陶泥板上所记录的结果如出一辙。当然,在《几何原本》中这些成果已经转变为在严格基础上被证明的普遍定理,从而被赋予崭新意义。但这显然就为希腊数学曾经受到巴比伦某些数学成果的启发、刺激而萌芽、发展,提供了坚强有力的证据(§5.2,特别是表5.1)。那也就是说,像泰勒斯、毕达哥拉斯那些早期哲人的数学意识乃至具体认识,的确可能如传说的那样,是在其游历中得之于“东方”的;又或许如《奥德赛》所描述的那样,是通过社会上各种渠道,间接吸收了“东方”数学成果。除此之外,我们还有若干证据表明,巴比伦的几何代数学一直没有消失,而是成为巴格达地区的民间传统,而这颇有可能就是伊斯兰代数学的根源(§8.3)。倘若如此,那么它之影响古希腊数学也就不足为奇了。所以,无论其具体途径如何,我们都不能不承认,希腊科学的渊源极有可能上溯至将近四千年前之古巴比伦文明。
[1]
各行顺序数则是根据
d/c的
值从接近
 递减至接近
递减至接近
 ,也就是说,相关三角形的其中一角从45°递减至30°左右。
,也就是说,相关三角形的其中一角从45°递减至30°左右。
[2] 根据多方面的最新考证,特洛伊(希腊文为 Tрoía )当是赫梯王国的属邦韦鲁沙(Wilusa),它在公元前1200年前后多次遭受希腊半岛上迈锡尼文明众多部落的联军攻击,这些部落的名称、方位在《伊利亚特》的所谓“舰队名录”中一一列出,至今还可以详细考核。因此特洛伊战争所反映的虽然未必是单一次庞大战争,却很可能是多次战役的实况。详见Latacz 2004的专门研究,至于Cline 2013则是此问题更精简的最新介绍。
[3] Odyssey 17.382-386,作者译文。引用此段的,尚见West 1997,p. 611;Burkert 1992,p. 6。



