基于数字岩芯的微观孔隙可视化流动模拟
摘要： 依托高精度扫描成像技术日趋成熟，数字岩芯分析技术在油气田开发工程中被广泛应用。由于其研究方法种类多、理论性强、差异大，渤海油田现阶段尚无成熟的技术开展数字岩心渗流模拟分析。本文基于渤海S油田东营组砂岩储层的真实数字岩芯，利用灰度处理、图像二值化、边界跟踪等图像处理技术实现岩石骨架提取、孔隙网络建模；基于格子玻尔兹曼方法，采用单松弛模型、非平衡反弹边界，构建流动系统，开展三维孔隙流动可视化模拟。利用本文方法可实现数字岩芯孔隙度-渗透率快速计算，实例表明，模型计算孔隙度-渗透率关系与油田实际误差低于4.0%。
关键词： 格子玻尔兹曼方法；数字岩芯；流动模拟；渗透率
1 引言
数字岩芯技术是一种依托高精度成像设备在岩芯孔隙级层面建模，继而分析储层物性参数的技术，目前已成为一种较为成熟、可用于油气田开发工程的分析技术。相对于传统室内岩芯实验，数字岩芯以其实验周期短、实验可重复、微观因素可控、节约岩芯等优势被广泛关注及应用。数字岩芯扫描分辨率已达到纳米级，也将油气流动研究推进微观孔隙流动研究的大门 [1] 。
数字岩芯孔隙流动，因其具有异常复杂的孔隙空间，孔隙和骨架的边界极不规则，直接求解Navier-Stokes方程不太符合实际，有限元、有限体积、有限差分等方法也难以处理异常复杂边界 [2-3] 。格子玻尔兹曼方法（Lattice Boltzmann Method，LBM方法），作为介观尺度计算流体力学方法，具有介于微观分子动力学模型和宏观连续模型的介观模型特点，因其流体相互作用易于描述、复杂边界易于设置、易于并行计算等优势，逐渐被应用到多孔介质复杂空间流动模拟。
近年来，基于格子玻尔兹曼方法的多孔介质流动模拟的研究较多，其多孔介质模型主要由二维图像切片通过数值重构所获得，常用数值重构方法包含模拟退火法、多点统计法、马尔可夫链-蒙特卡洛法（MCMC）等。虽然数值重构模型能够具有与切片相同的特征参数，但其与真实雅安心结果相差也较大。基于真实数字岩芯开展的孔隙流动模拟相对较少 [4-6] 。
本文基于渤海S油田东营组某砂岩数字岩芯开展研究，应用格子玻尔兹曼方法进行三维孔隙流动模拟，并开展数字岩芯孔隙度-渗透率关系分析。实例计算结果对标油田实际，渗透率误差低于4.0%。
2 数字岩芯孔隙网络模型
本文基于渤海S油田东营组某砂岩岩芯（深度1379.0～1379.1m）CT扫描结果开展孔隙网络建模。扫描对象包括：全直径岩芯（扫描分辨率0.1mm）、岩芯柱塞（扫描分辨率13μm）、柱塞子样（扫描分辨率2μm），见图1。
图1 渤海S油田某砂岩岩芯扫描结果
根据岩芯扫描切片分析可知，全直径岩芯由于扫描精度较低，尚不能有效识别岩芯孔隙；岩芯柱塞扫描分辨率中等，能够识别岩芯孔隙分布；柱塞子样扫描分辨率较高，能够有效识别岩芯孔隙。考虑岩芯孔隙分布的非均匀性、随机性，柱塞子样由于其分辨率高，其扫描区域较小，对岩芯的表征不及岩芯柱塞，因此选用岩芯柱塞扫描结果开展孔隙网络建模。
2.1 数字岩芯灰度处理及数据二值化
在数字岩芯分层CT扫描切片过程中，受扫描设备分辨率影响产生一定程度的噪声，干扰骨架边界识别，因此需要开展灰度图像降噪处理。常用降噪处理方式有：均值滤波、中值滤波。由于中值滤波属非线性降噪技术，能够相对有效地保护边缘信息，在数字岩芯灰度图像降噪处理的同时兼顾保护骨架边界的不规则形状。因此，本文选用中值滤波技术对数字岩芯扫描图像进行噪声过滤，图2为噪声过滤前后对比情况。
图2 数字岩芯某扫描切片局部原始及过滤后灰度图像
数字岩芯为灰度图像堆栈，而用于流动模拟的孔隙网络模型仅关注骨架、孔隙两种状态，需要进行阈值分割处理，将灰度图像二值化，用1代表骨架，0代表孔隙。本文采用单阈值处理方式，数字岩芯数据体设定单一阈值，灰度值大于阈值视为骨架、小于阈值视为孔隙。选用试凑法进行阈值选取，当阈值取10 9 时，中等分辨率（13μm）的柱塞单元与高分辨率（2μm）柱塞子样的孔隙度一致，以该值为单一阈值进行数字岩芯图像二值化，图3为二值化处理后效果图。
图3 数字岩心图像二值化处理后
2.2 数字岩芯孔隙网络建模
数字岩芯孔隙网络模型，体素主要包含3种状态，即孔隙、骨架、边界。数字岩芯二值化处理后仍需开展边界识别、三维重建。
边界识别，需要筛选出骨架与孔隙接触的边界体素，进行单独标记。本文采用图像处理中边界跟踪算法 [7] ，按照八连通关系，对数字岩芯二值图像进行边界跟踪。数据处理后，数字岩芯体素只包含0、1或23种状态，2代表骨架，1代表边界，0代表孔隙。如图4中，深灰色为骨架，浅灰色为边界，黑色为孔隙。
图4 数字岩芯（局部）边界追踪后图像
三维重建，即将边界识别后的切片图像堆栈构建成为孔隙网络模型，根据模型体素状态确定是否为骨架、边界或孔隙。图5中，三维网格模型即孔隙网络模型。
图5 数字岩芯（局部）孔隙网络模型
3 格子玻尔兹曼方法流动模拟
基于本文数字岩芯处理技术，可以将灰度图像堆栈处理成为三维网格模型。在此基础上，选取适宜的格子玻尔兹曼方法模型、确定模型边界条件，即可开展三维数字岩芯流动模拟。
3.1 格子玻尔兹曼方法模型
格子玻尔兹曼模型主要由三部分组成，即平衡态分布函数、演化方程、离散速度模型。
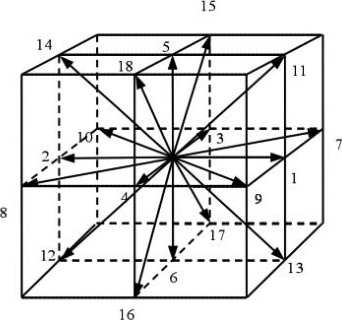
图6 D3Q19速度模型
本文研究对象为三维数字岩芯，因此选用常见的D3Q19模型（空间维数为3，离散速度方向19，如图6），公式（1）即为离散速度模型。
公式中， i =0，1，2，…，19，代表模型包含19个速度方向； e i 代表 i 方向上的速度； c s 表示无量纲格子声速； ω i 代表权重系数；
演化方程及平衡态分布函数选用较为常用的单松弛模型及对应分布函数（无附加作用力项），公式（3）即为单松弛模型演化方程，公式（4）即为单松弛模型平衡态分布函数。
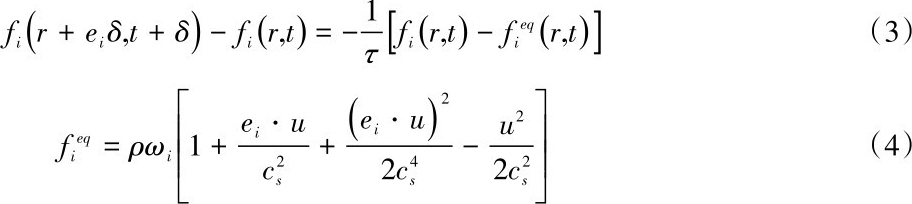
公式中，
r
代表粒子的空间位置；
t
代表时间；
δ
代表时间步长；
代表离散的速度空间中的局部平衡态分布函数。
3.2 模型边界条件
孔隙网络模型为立方体，模型壁面包含流入壁面、流出壁面、边界壁面；系统内，格点包含骨架、孔隙、边界3种状态。其中，模型6个壁面及系统内边界格点都需要设置边界条件。本文选用的室标准反弹边界、压力边界。
标准反弹边界，指在某微粒格点上，微粒按照运动轨迹运动至边界格点，其后微粒发生反弹，反弹后沿原运动轨迹相反的方向运动。标准反弹边界常用于描述无滑移壁面反弹，即沿壁面方向无速度梯度的反弹。孔隙网络模型中，除流入/流出面外，其余所有壁面、系统内边界格点均按照无滑移壁面处理。
压力边界条件，参考Zou等人根据非平衡反弹格式思想提出的动力学压力边界格式
[8]
。在孔隙网络模型流入面处压力值已知，即
（
P
in
为流入面压力，
ρ
in
为流入微粒密度）已知，而流入面速度未知。Zou等人提出的边界处沿壁面方向速度分量为0，水平速度分量
u
x
未知，结合离散速度模型及平衡态分布函数与宏观物理量的关系，联立方程组即可求解边界速度。
3.3 三维数字岩芯孔隙流动模拟
基于数字岩芯孔隙网络模型，采用格子玻尔兹曼方法单松弛模型，进行三维孔隙流动模拟。设置网格尺寸为100μm×100μm×100μm，流动介质为气体，设置 X 方向流入面与流出面压差为0.020MPa，网格步长为1μm，松弛时间为1ms，模拟结果如图7所示。
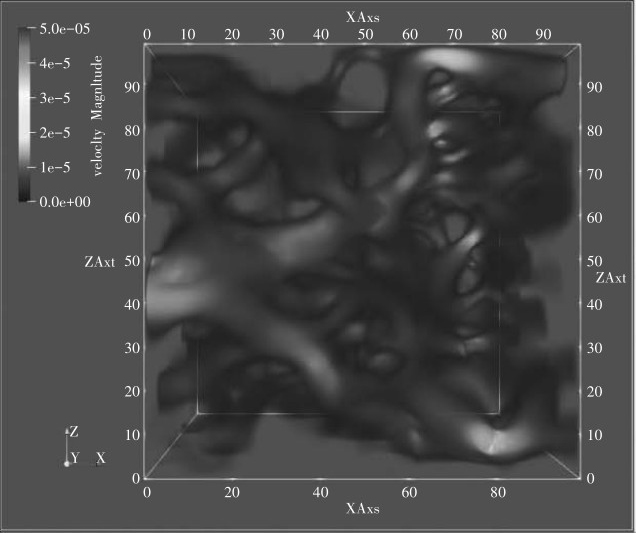
图7 岩芯柱塞孔隙三维稳态流动速度场分布
利用格子玻尔兹曼模型，结合格子条件与宏观条件下物理量的转换关系，可以计算孔隙模型出入端压差、流量，继而获得稳态条件下孔隙过流量，以此计算模型渗透率。
4 岩芯柱塞孔隙度-渗透率分析实例
本文选用的渤海S油田东营组某砂岩岩芯（深度1379.0～1379.1m）CT扫描结果，其中岩芯柱塞数据体扫描尺寸（单位：像素）为2000×2000×1500，考虑到格子玻尔兹曼方法针对每一像素建立网格进行运算，如果针对全柱塞孔隙流动模拟较为困难。因此，在实际流动模拟过程中，提出对数字岩芯拆分、局部流动分析、统计回归的方法分析柱塞孔隙度-渗透率关系，如图8所示。
图8 岩芯柱塞取样分组及部分孔隙流动模拟图
针对柱塞样品选取8组孔隙度有所差异的岩芯样品，并分别进行孔隙度、渗透率统计，并将统计回归后的孔隙度-渗透率关系与油田实际散点对比。如图9所示，统计结果显示，格子玻尔兹曼方法孔渗关系回归结果与油田实际误差低于4.0%。
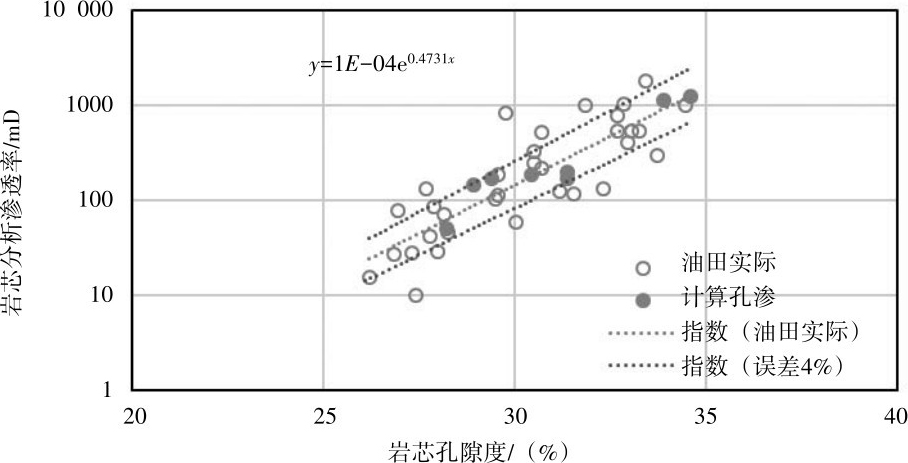
图9 模型计算孔隙度-渗透率关系与油田实际对比图
5 结论
①基于数字岩芯扫描数据结果，利用灰度处理、图像二值化、边界跟踪等方法，实现数字岩芯孔隙网格建模。
②基于三维格子玻尔兹曼模型，选用标准反弹边界、压力边界实现对孔隙网络模型的流动模拟。
③开展数字岩芯孔隙度-渗透率分析研究，模型计算结果与油田实际误差低于4.0%，证明该方法的准确性。
参考文献
[1] 刘雪锋，张伟伟，孙建孟．三维数字岩芯建模方法综述[J]．地球物理学进展，2013，28（6）：3066-3072.
[2] 何雅玲，王勇，李庆．格子Boltzmann方法的理论及应用[M]．北京：科学出版社，2008.
[3] 郭照立，郑楚光．格子Boltzmann方法的原理及应用[M]．北京：科学出版社，2008.
[4] 张顺康，陈月明，侯建，等．岩石孔隙中微观流动规律的CT层析图像三维可视化研究[J]．石油天然气学报（江汉石油学院学报）. 2006，28（4）：102-106.
[5] 王春生，刘洋，孙启冀，等．基于数字岩芯技术研究低渗砂岩渗流特征[J]．物探化探计算技术，2017，39（4）：573-577.
[6] 朱益华，陶果，方伟，等．3D多孔介质渗透率的格子Boltzmann模拟[J]．测井技术，2008，32（1）：25-28.
[7] 邓士超，李伟明，龙芋宏，等．一种改进的二值图像边界跟踪与边界链码获取算法[J]．激光与光电子学进展，2018，55（6）：147-153.
[8] ZOU Q S，HE X Y. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model[J]. Physics of Fluids，1997，9∶1591-1597.
