3.2 芝诺、哥德尔和时空旅行
埃利亚的芝诺(Zeno of Elea,约公元前490年—公元前430年)是一位伟大的哲学家,师从巴门尼德(Parmenides,公元前5世纪)。作为一名虔诚的学生,芝诺推广了老师的哲学观念,并替老师挡住了所有批评。巴门尼德有一个神秘的哲学观点,认为世界是“一”,变化和运动都只不过是幻象,人经过足够的训练之后就能识破这种幻象。为了论证巴门尼德的观点是正确的,芝诺提出了几个思想试验和悖论,用这种方式指出,认为世界“多元”而非“单一”,或者变化和运动真实发生的观念不符合逻辑。在本节中,我将关注其中4个阐述运动实乃幻象的思想实验。由于空间和时间中总是在发生运动,芝诺的悖论将挑战我们对这些显而易见的观念的直觉认知。
不幸的是,芝诺的大多数原始文稿已经丢失了。我们对这些悖论的认识在很大程度上来自那些想要证明他错了的人。亚里士多德先阐述了芝诺的一些观点,然后再将它们一一驳斥。因为芝诺的观点总是被摒弃,所以我们很难弄清他最初的意图是什么。这不应该成为阻止我们的理由,因为我们最关心的不是芝诺实际上说了什么;我们更感兴趣的是弄清楚我们的直觉是否出了毛病,以及我们可以如何调整它。这些观点不应该被等闲视之。它们已经烦扰了哲学家们将近2500年了。无论是否同意芝诺的论断,他都是不能被忽视的人。
芝诺关于运动的第一个也是最简单的悖论是二分法悖论(dichotomy paradox)。设想一下,某个聪明的懒人某天早上从床上醒了过来。他试图从床边走到房间的门口(见图3-2)。

图3-2 芝诺的二分法悖论
要想走完到门口的全部路程,他必须先来到这段路程1/2的位置。抵达这个位置之后,他仍然必须向前走1/4的路程。到达那里之后,前面还有1/8的路程必须要走。抵达每个节点后,他都必须再向前走剩下路程的一半。似乎这个人永远也无法走到门口。换句话说,如果他真的想走到门口,他就必须完成一段无穷无尽的过程。由于人无法在一段有限的时间里完成一段无穷无尽的过程,他永远走不到门口。
他可以用更多逻辑推理进一步正当化自己的懒惰。要走到门口,就必须先走到中点。要走到中点,就必须先走到1/4处,而在1/4处之前,就必须先走到1/8处,……在进行任何动作之前,他都必须先完成这个动作的一半。无论去任何地方,他都需要完成无限多次的过程。无限多次的过程需要无限多的时间。谁拥有无限多的时间?为什么还要起床呢?
芝诺悖论并不只是关于运动,它与任何需要完成的任务都有关。为了完成一项任务,必须先完成这项任务的一半,然后再继续剩下的任务。这表明在一段有限的时间里,不仅运动是不可能的,执行任何任务甚至任何变化的发生都是不合理的。
对于芝诺的这个小小的思维难题,我们该如何解决呢?毕竟,我们的确曾在一段有限的时间抵达了旅程的终点,而且当我们早上起床之后,我们的确可以做到一些事情。与本书的主题十分相符的是,芝诺悖论可以通过矛盾来证伪。我们假设某件事(错误的),然后通过逻辑推导出矛盾或显而易见的谬误。在这里,我们的结论是不存在运动或变化,然而事实上我们总是见到运动和变化。那么我们的错误假设到底是什么呢?
数学家会争辩说,完成一项无限的任务并不存在问题。看看下面这个无限求和算式吧:
1/2+1/4+1/8+1/16+1/32+…
缺乏相应知识的人会说省略号意味着这个算式会无穷无尽地延伸,所以总和将是无穷大。然而总和是有限的数字1。 [1]
我们可以用一种优美的平面几何的方式展示这个算式等于1。设想一个边长为1的正方形,如图3-3所示。
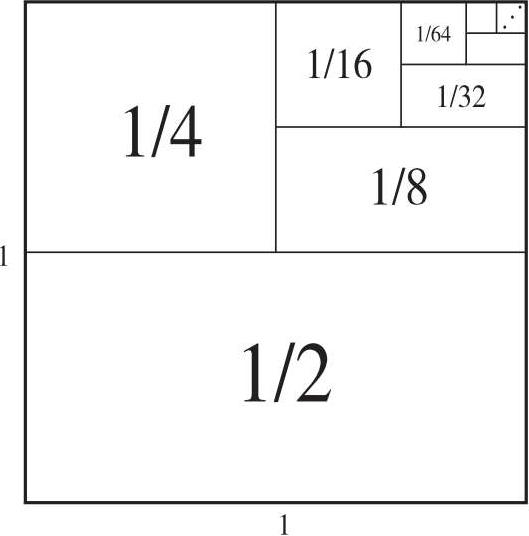
图3-3 以平面几何表示的无限求和算式
可以看到,这个正方形由它自身的1/2加上它的1/4再加上1/8再加上……组成。每个剩余的部分都可以进一步分成两半。显而易见,整个正方形覆盖的总面积是1。
然而,如果某个数学家宣布这样就解决了芝诺这个在有限时间内完成无限过程的悖论的话,那他在某种程度上就是不老实的。毕竟,这位数学家并没有将这个无穷算式的每一项都逐个加起来。他只是展示出了前面几项,然后用省略号表示后面还有无限多个加数。他耍了个花招,将要加上的各项内容简略地表示了出来。如果有人坐下来,将所有无穷无尽的各项逐个加上去,一定会花无限多的时间。
一个更好的办法是声称芝诺的推理中存在问题,问题在于他假设空间是连续的。这就是说空间看起来就像一条线,是无限可分的——在两点之间存在无限多个点。只有在这样的假设之下,才能描述二分法悖论。如果是相反的情况,不妨设想我们正使用一台拥有几百万像素的老式电视观看懒人走向门口。随着他的走动,他在穿越这些像素。他穿过了电视机屏幕的一半像素,然后穿越了剩余像素的一半。最终电视机里的懒人会距离门口只有1个像素,然后他就来到了门口。他不可能只穿过半个像素。一个像素要么被穿过,要么不被穿过。在电视屏幕上,懒人抵达目的地不会产生任何问题,芝诺的悖论也烟消云散了。或许我们也能够对真实的世界做出同样的判断。或许空间是由离散的点构成的,相邻的点彼此独立,任意两点之间其他点的数量都是有限的。如果是这样,我们就不用再为二分法悖论头疼了。如果我们假设空间是离散的,我们就能理解为什么这位懒人能够走到门口了:他只需要穿过一系列数量有限的点。在某一时刻,剩下的间隔再也无法一分为二。在这种类型的空间中,物体的运动形式是从一个离散的点跳跃到另一个离散的点,而不会进入它们之间。
使用第1章中的语言,我们可以说这是一个悖论,因为如果我们假设空间是连续的:
空间是连续的
 运动是不可能的。
运动是不可能的。
由于这个世界上无疑存在运动,我们的假设推导出了谬误的结果,所以我们可以判断,空间是不连续的。相反,它是离散的,或者说分成众多微小的“空间原子”。
对于量子力学的研究者而言,这种离散空间的概念相当熟悉。
 物理学家会谈论
普朗克长度
(Planck's length)这个术语,它约等于1.6162×10
-35
米,比它更小的长度是无法测量出来的。从某种意义上说,不存在比它更小的东西。物理学家向我们保证,物体在运动时总是从一个普朗克长度移动到另一个普朗克长度。在高中化学课上,我们学到原子中的电子围绕原子核分层高速运动。当某个原子吸收能量时,电子会发生“量子跃迁”,从自己原本的那层跳跃到下一层。它们不会进入各层之间的空隙中。或许我们的懒人先生也进行了这样的量子跃迁,因此最终能够走到门口。
物理学家会谈论
普朗克长度
(Planck's length)这个术语,它约等于1.6162×10
-35
米,比它更小的长度是无法测量出来的。从某种意义上说,不存在比它更小的东西。物理学家向我们保证,物体在运动时总是从一个普朗克长度移动到另一个普朗克长度。在高中化学课上,我们学到原子中的电子围绕原子核分层高速运动。当某个原子吸收能量时,电子会发生“量子跃迁”,从自己原本的那层跳跃到下一层。它们不会进入各层之间的空隙中。或许我们的懒人先生也进行了这样的量子跃迁,因此最终能够走到门口。
让我们重新思考一下图3-3。如图所示,这个正方形被无限分割了下去。但只有当我们将这个正方形当成一个数学对象时,这种情形才有可能。在数学中,每个代表一段距离的实数都可以一分为二,因此我们才能永远继续切割下去。相比之下,让我们将这个正方形想象成一张纸。开始的时候,我们可以用越来越精细的剪刀将纸裁剪得越来越小。这样的做法可以持续一段时间,但最终我们会到达原子水平,再也无法进一步切割。对于任何由原子构成的具体物体来说都是如此。我们被迫得出结论,从物理学的角度来看,图3-3中描绘的正方形并不适用于正方形的纸张。实数可以无限分割,但纸不可以。芝诺迫使我们提出了空间(不是由原子构成的)是否可以无限分割这个问题。如果能够无限分割,懒人先生就不能抵达自己的目的地。如果不能的话,说明一定存在离散的“空间原子”,使用连续实数表示的数学不能够作为空间的合适模型。 [2]
然而,我们不能如此轻率地断定空间是离散的而不是连续的。世界看上去的样子当然不像是离散的。运动给人的感觉就是连续的。数学物理的许多内容以微积分为基础,这需要假设真实世界是无限可分的。在量子力学和芝诺的哲学理论之外,连续实数是能够完美适用于物质世界的模型。我们建造火箭和桥梁时使用的数学就假设世界是连续的。让我们不要这么快就抛弃它吧。

关于运动的第二个芝诺悖论是 阿喀琉斯(Achilles)和乌龟 的故事。阿喀琉斯是现代DC漫画中闪电侠(The Flash)这个角色的古希腊版本,他是城里跑得最快的人。有一天他和一只慢吞吞的乌龟进行了一场跑步比赛。为了让这场比赛更加有趣(还因为阿喀琉斯是个心地善良的暖男),阿喀琉斯让乌龟先出发,如图3-4的第一行所示。
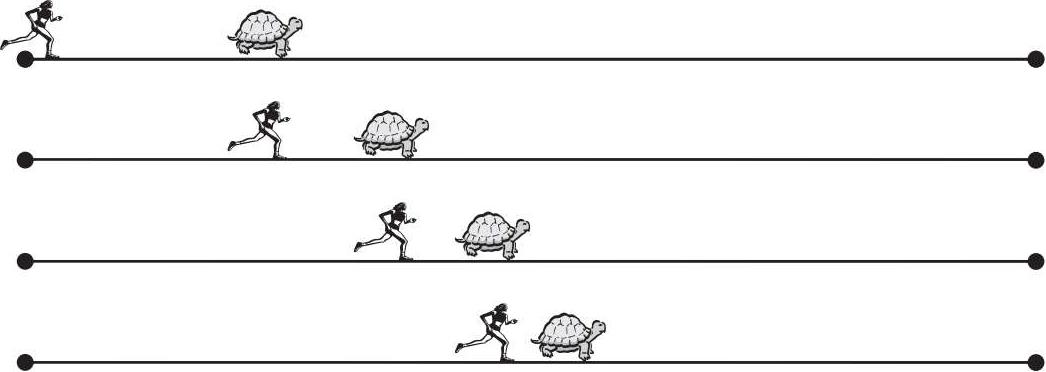
图3-4 阿喀琉斯追不上乌龟
问题在于,阿喀琉斯要想超过乌龟,就必须先通过乌龟开始的起点(如图3-4的第二行所示)。当阿喀琉斯跑到这一点时,乌龟已经向前移动了一段距离。再一次地,阿喀琉斯要想超过乌龟,他必须先抵达乌龟已经移动到的地方。在每个节点,阿喀琉斯都越来越接近恼人的乌龟,但他永远也无法追上它,更别说超过它了。
针对这个悖论可以进行类似的数学分析。在微积分中,我们说当 x 趋近于正无穷时,1/ x 的极限为0。也就是说, x 越大,1/ x 就越接近0。由于正无穷不是一个数, x 永远不会达到正无穷,所以1/ x 永远不会等于0。但是极限的概念让这个等式有了意义。相似地,阿喀琉斯和乌龟之间的距离永远不会真正为零,但这个距离的极限等于零。我们同样能在这种类比中找到瑕疵。数学上的极限概念是一种把戏。因为对于任何有限的数,1/ x 都不会真正等于0,也就是说,在任何一段有限的时间里,阿喀琉斯都不会真正追上乌龟。
如果我们假设跑道是由离散的点构成的,这个悖论同样也会烟消云散。阿喀琉斯比乌龟跑得快这个事实只是意味着在一段相同的时间里,他跑过的离散点的数量更多。所以最终阿喀琉斯将超过乌龟。离散空间可以解答这个悖论,但是同样,我们必须小心谨慎。我们在抛弃连续空间的观念时应该怀着极大的忧虑,因为这个数学模型在普通物理学中的适用性非常好。
在第三个悖论中,芝诺甚至不再关心一个动作是否能够完成。他攻击的是运动这个观念本身。在 飞矢不动悖论 (arrow paradox)中,我们被要求设想一支在空间中飞行的箭。在每一个瞬间,这支箭都处于某个特定的位置上。如果我们将时间设想成一系列连续的“现在”,这些“现在”分开了身后的“过去”和前面的“将来”的话,那么对于每一个“现在”,这支箭都位于某个特定的位置上。在时间的每一个点上,箭都位于某个确定的位置,没有运动。问题是,这支箭在什么时候运动呢?如果它在每个“现在”都不运动,那它在何时运动呢?
如果我们引入离散的概念,这个悖论也会迎刃而解。不过我们在这里要说的不是强调空间是离散的,而是时间是离散的。在时间的每个单独的点上不存在运动。但是时间会从一个点跳跃到另一个点上,运动和这一瞬的跳跃同时发生。换句话说,时间是离散的,不是连续的。我们为什么看不到这些神奇的跳跃呢?我们在看电影时以为自己看到的是连续动作,原因是一样的。事实上,电影是由离散的众多静止画面组成的,这些画面之间不存在运动。因为单独时间点彼此十分接近,而且这样的时间点非常多,所以才产生了连续性的假象。
这个悖论基本描述了下列推导过程:
时间是连续的
 运动是不可能的。
运动是不可能的。
又是相同的情况,既然“运动是可能的”是显而易见的事实,我们可以得出结论:时间是不连续的。
这个悖论也存在相应的数学类比。将时间设想为代表实数的线。实数线上的每一点都对应着一个“现在”。而每一个“现在”都是没有宽度的。上九年级的时候,你已经学到数学中的实线是由无限多个点组成的,而且每一点的长度都为零。那么一段有长度的实线如何由没有任何宽度的点组成呢?零乘以任何数都等于零。你的九年级数学老师在向你撒谎吗?实数线的概念是对的吗?我们是否应该摒弃它?
再一次地,为了接纳离散时间观念而摒弃连续时间观念也存在问题。现代物理和工程学都以时间连续这一现象为基础。所有公式都含有一个连续的时间变量,通常表示为 t 。然而,正如芝诺向我们展示的那样,连续时间的观念是不符合逻辑的。
第四个也是最后一个针对运动的悖论是 运动场悖论 (stadium paradox)。芝诺想让我们想象一下竞技场上的三支游行队伍,如图3-5所示。
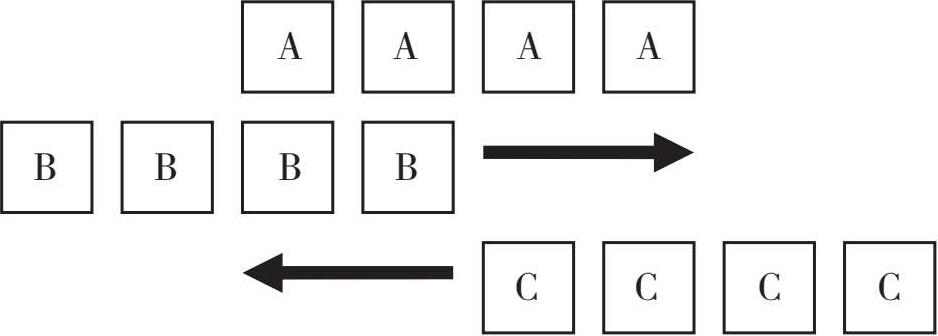
图3-5 三支游行队伍同时出发
A队伍静止不动,在A队伍身后,B队伍和C队伍正在以相同的速度相向而行。经过一段时间后,这三支游行队伍就会如图3-6所示。
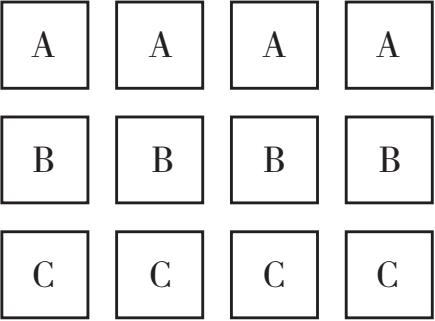
图3-6 结束时的三支游行队伍
值得注意的是,在一段相同的时间里,B队伍最前面的成员经过了2个A队伍成员和4个C队伍成员。既然A队伍和C队伍长度相等,B怎么能经过数量不同的A队伍成员和C队伍成员呢?显而易见的答案是,A队伍是静止的,而C队伍是运动的。速度和相对速度之间存在差别——亚里士多德使用同样的理由驳斥了这个悖论。当我们开车或坐在车里时,总是会发现路边房屋掠过的速度和对面来车掠过的速度有明显差别,我们对此已经习以为常了。
或许我们不该如此蔑视巴门尼德忠实的学生。事实上并没有办法确定芝诺最初的意图是什么,因为我们只有来自亚里士多德的一段简单的讨论。现代思想家假设了一个稍微复杂一些的情景。在之前的三个悖论中,我们看到如果将空间和时间想象成离散的或者量子化的,这些问题就都迎刃而解了。在最后这个悖论中,让我们假设空间和时间都是离散的。设想各游行队伍的成员都拥有可能情况下最小的离散尺寸。与此同时,想象B队伍以可能情况下最快的速度移动。B队伍从图3-5的位置移动到图3-6的位置需要两秒。在这样的速度下,B队伍的每个成员每秒经过一个成员。这是B队伍经过两个A队伍成员所需要的可能情况下最短的离散时间。在这段最短的时间内,B队伍是如何经过数量为两倍的C队伍成员的?这意味着B队伍经过C队伍的速度还要更快。对于B队伍的成员而言,这样的情景看起来像是什么?在B队伍眼中,C队伍要么遗漏了两个成员,要么移动得比允许的最大速度还要快。对竞技场悖论的解读意味着,“空间和时间是离散的”这样一种假设也是有问题的。
空间和时间是离散的
 谬误。
谬误。
我们必须断定,空间和时间不是离散的。
事实究竟如何?空间和时间是连续的还是离散的?一方面,竞技场悖论指出空间和时间应该是连续的。另一方面,如果我们将空间和时间设想为离散的,前三个悖论就能解决。答案很简单,我们不知道空间和时间的性质。
这种冲突是当代物理学的一场对立的缩影。20世纪物理学的两大成就是相对论和量子论。
 这两大革命性的科学进展基本上描述了物理世界的大部分现象。相对论涉及的是引力和宏观物体,而量子论涉及的是其他力和微观物体。然而,这两大理论彼此之间是存在冲突的。它们之间冲突的主要原因之一就在于,相对论认为空间和时间是连续的,而量子论认为空间和时间是离散的。在大多数情况下,由于这两种理论的应用领域不同,这种冲突并不会让我们感到困扰。然而对于某些特定的现象,如黑洞,又被称为“空间的边缘”,这种冲突就会十分明显。既然我们不能同时拥有互相冲突的物理理论,那么一定是因为我们还不知道最终的故事。关于空间和时间的结构,我们尚无定论。
这两大革命性的科学进展基本上描述了物理世界的大部分现象。相对论涉及的是引力和宏观物体,而量子论涉及的是其他力和微观物体。然而,这两大理论彼此之间是存在冲突的。它们之间冲突的主要原因之一就在于,相对论认为空间和时间是连续的,而量子论认为空间和时间是离散的。在大多数情况下,由于这两种理论的应用领域不同,这种冲突并不会让我们感到困扰。然而对于某些特定的现象,如黑洞,又被称为“空间的边缘”,这种冲突就会十分明显。既然我们不能同时拥有互相冲突的物理理论,那么一定是因为我们还不知道最终的故事。关于空间和时间的结构,我们尚无定论。
芝诺悖论最令人惊叹的一面在于,它们来自2500年前,而且关注的是如此终极的主题。空间、时间和运动的本质是什么?我们无法确定的是,这位来自埃利亚的朋友是否向我们发出了最后这个疑问。
既然我们在讨论空间、时间和逻辑的关系,那就来谈谈时间旅行悖论吧。我们首先必须问问自己,穿越到过去
 意味着什么。如果我穿越到1776年的费城大陆会议,见证了《独立宣言》的签署,那意味着什么?如果我奇迹般地穿越回去,目睹了签字盛况,那么我在那个炎热的七月天身处那个会议室的事实就意味着这不是原本的大陆会议。毕竟原本的大陆会议的会场没有我的存在。换句话说,如果原本的大陆会议一共有150人在场,当我穿越回去的时候,会有151人在场。这不是原本的会场。我穿越回去的会场和原始的会场之间存在重大区别。我穿越回去的到底是何时何地?有一点是确定的:不是1776年的大陆会议。
意味着什么。如果我穿越到1776年的费城大陆会议,见证了《独立宣言》的签署,那意味着什么?如果我奇迹般地穿越回去,目睹了签字盛况,那么我在那个炎热的七月天身处那个会议室的事实就意味着这不是原本的大陆会议。毕竟原本的大陆会议的会场没有我的存在。换句话说,如果原本的大陆会议一共有150人在场,当我穿越回去的时候,会有151人在场。这不是原本的会场。我穿越回去的会场和原始的会场之间存在重大区别。我穿越回去的到底是何时何地?有一点是确定的:不是1776年的大陆会议。
 这个困境说明,即便是理解时间旅行本身的基础观念,也是非常困难的。
这个困境说明,即便是理解时间旅行本身的基础观念,也是非常困难的。
尽管如此,还是让我们暂时设想一下我们理解了时间旅行的真正意义,而且不妨再让我们设想一下,这样的过程其实是可能的。如果时间旅行是可能的,时间旅行者可以回到过去的时间,开枪射杀他当时还是单身汉的祖父,以此确保这位时间旅行者永远不会出生。如果他永远不会出生,那么他永远无法射杀自己的祖父。达成这样充满悖论的效果并不一定需要杀人行凶。时间旅行者可以确保自己的父母永远不会有孩子, [3] 他还可以只是回到过去,确保自己将来不进入时间机器。这些动作会导致矛盾,因此不可能发生。时间旅行者不应该射杀自己的祖父(且不论道德上的理由),因为如果他射杀了自己的祖父,将来他就不会存在,无法穿越回来射杀自己的祖父。于是他通过完成一项动作来确保这一动作无法被完成。这一事件是自我指涉的。通常情况下,一个事件只会影响其他事件,但在这里,一个事件影响了自身。使用第1章的语言,我们是在指出:
时间旅行
 矛盾。
矛盾。
由于世界不允许矛盾存在,我们必须通过某种方式避免这种矛盾。要么时间旅行是不可能的,要么即使时间旅行是可能的,一个人也无法制造出杀死更早版本的自己这样的矛盾。我们更喜欢哪种不可能性呢?
阿尔伯特·爱因斯坦的相对论告诉我们,我们对宇宙的常规认知方式决定了时间旅行是不可能的。1949年,爱因斯坦的朋友,他在普林斯顿的邻居库尔特·哥德尔(Kurt Gödel,1906—1978)搞了一点物理学兼职,撰写了一篇关于相对论的论文。哥德尔构建了一种看待宇宙的数学方法,这种方法令时间旅行变得可能。在这样的“哥德尔宇宙”中,回到过去非常困难,但不是没有可能。作为自亚里士多德以来最伟大的逻辑学家,哥德尔充分意识到了时间旅行中的逻辑问题。数学家兼作家鲁迪·鲁克(Rudy Rucker)讲述了他对哥德尔的一次采访,鲁克在这次采访中问到了时间旅行的悖论。相关段落值得在此引用:“‘时间旅行是可能的,但没有人能够杀死过去的自己。’哥德尔笑了笑,然后得出了结论:‘这个推导被严重忽视了。逻辑的力量十分强大。’”
 哥德尔回答道,宇宙不会让你杀死过去的自己。正如理发师悖论说明遵守某些严格规则的村庄不可能存在一样,这个物质世界也不允许你做出某个会导致矛盾的行为。
哥德尔回答道,宇宙不会让你杀死过去的自己。正如理发师悖论说明遵守某些严格规则的村庄不可能存在一样,这个物质世界也不允许你做出某个会导致矛盾的行为。
这将让我们提出更多令人兴奋的问题。如果某个人带着一把枪回到过去,朝更早的自己开枪,会发生什么?宇宙如何阻止他?他不会产生犯下这桩卑劣罪行的自由意志呢,还是枪会卡壳呢?如果子弹终究被发射出去,瞄得也很准,子弹会在距离他身体很近的地方停下来吗?生活在一个不允许矛盾的世界里,实在是令人困惑。
[1]
这实际上是最容易证明的定理之一,值得花一分钟时间展示它的证明过程。假设我们不知道下面这个式子的总和是多少,并将其称为
x
:
x
=1/2+1/4+1/8+1/16+1/32+…
再重申一次,我们不知道
x
是多少,但是通过描述它,我们就能操纵它了。思考(1/2)
x
。根据算术分配率,我们知道1/2(
a
+
b
+
c
)=(1/2)
a
+(1/2)
b
+(1/2)
c
。
这不仅适用于3个数,还适用于无限多个数。于是我们还能得到
(1/2)
x
=(1/2)×(1/2)+(1/2)×(1/4)+(1/2)×(1/8)+(1/2)×(1/16)+…=1/4+1/8+1/16+1/32+…。
用
x
减去(1/2)
x
,我们得到
x
-(1/2)
x
=(1/2)
x
或
x
-(1/2)
x
=(1/2+1/4+1/8+1/16+…)-(1/4+1/8+1/16+1/32+…)=1/2。即(1/2)
x
=1/2
即
x
=1。证明完毕。
[2] 亚里士多德写道:“此外,原子构成物体的观念肯定会和数学产生冲突,还会让许多常见观念、显而易见的数据和感知变得无效。”[《论天》( De Caelo ),303a21]
[3] 这是1985年的一部电影《回到未来》( Back to the Future )的主题。


