1.简化的开放货币经济

我们现在将详细阐述上文简单介绍过的模型。这里所说的“开放”是指，我们分析的国家身处全球经济体系之中，可以同其他国家开展贸易并从那里筹集资本。这是我们分析的一个关键出发点。如果经济是完全封闭的，我们就不能把国家与企业类比，也无法把增加法定货币的供给当作发行股票来解释。

在初始时期（时期0），这个国家可以开展规模为 k >0的投资项目，以提高其生产率。在中间时期（时期1），该国把初始商品禀赋 w 配置为消费（ c ₁ ）与生产投入（ w - c ₁ ）。在最末时期（时期2），该国实现产出 y 并将它们用于消费。我们首先看看在没有基础设施投资时，该经济会如何运行。此时只有两个相应的时期，时期1的生产阶段和时期2的消费阶段。你可以把这两个时期想象为一个永续国家的生命周期中的短暂时间窗口。

这个国家由完全等同的消费者和企业组成，在完全竞争的市场中开展活动。消费者的目标是更多的消费，企业的目标是更多的产出。除了这些基本目标和行为（以便反映经济的运行），我们尽可能保持模型的简单精练。相应地，我们把消费者设定为风险中性，其唯一目标是使整个生命周期的消费最大化。我们假设消费者在每个时期需要最低限度的生存消费，并将它标准化为0，由此必然得到： c t ≥0， t =1，2。消费者的效用函数如下：

U （c ₁ ,c ₂ ）= βc ₁ +c ₂

其中， β ≤1，所以消费者更愿意推迟而非提前消费。生命周期开始时，消费者在时期1有初始商品禀赋为 w >0。他们可以把这些禀赋储存起来，也可以出售给企业。我们假设储存行为缺乏效率，于是企业与消费者会在时期1发生交易，消费者用商品禀赋来换取企业手里的货币。具体来说，我们假设储存产品会贬值，如果禀赋 w 从时期1储存到时期2，它将贬值到 dw ，其中 d <1。在我们的大多数分析中，我们可以设定 d = β 且不会丧失一般性。

代表性竞争企业则会把消费品作为生产的一种投入品，其生产函数为：

y ≡ θf （x）

并且有 f′ >0， f″ ≤0，而 θ 是可能取两个值的生产率冲击： θ ∈{ θ L ， θ H }，其中 θ H > θ L >0。这里的 x 代表企业在生产中使用的投入品数量。我们假设生产技术只意味着企业能够用更多的投入得到更多的产出，而且投入品的使用符合收益递减特征。后一个假设并不严格需要，但可以带来便利，因为我们能由此获得一个均衡市场结果，让所有企业在时期1购买相同数量的投入品，然后在时期2生产相同数量的产出。

企业的初始法定货币禀赋给定为 m >0。企业在时期1利用这些货币去购买消费者的初始禀赋作为投入品，消费者则在时期2利用储存的货币去购买企业的产出。

企业归企业家拥有，后者的目标是实现时期2的产出最大化，并且他们在时期2的消费为最终产出的一部分： ψ ∈（0，1）。为尽量减少需要处理的参数数量，我们用 θf （ x ） =θ （1 -ψ ） F （ x ）来代表将被投入市场的最终产品，包括企业家消费部分的总产出为 θF （ x ）。我们用 m ₂ 来表示代表性企业在时期2结束时持有的现金数量，此时企业的持续经营价值将为 V （ m ₂ ），随 m ₂ 的增加严格递增。我们可以把价值函数 V （ m ₂ ）理解为继承了货币持有数量 m ₂ 的未来企业家能够用这些钱买到的未来投入品和消费品流的现值。这里要求的条件是货币在时期2结束时继续保有价值，否则，企业就不愿意把自己生产的产品交换成货币（Hahn, 1965，1982）。

在时期1，什么是把初始禀赋 w 划分为投入 x 和消费（ w - x ）的有效配置？对 x 的有效选择意味着对如下代表性消费者的效用最大化问题求解：

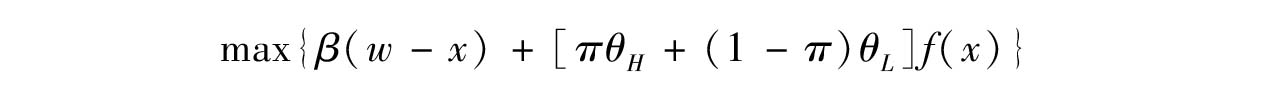
为避免分析中任何不必要的复杂性，我们把关注点放在 x = w 的角点解上。在此情形下，时期1完全投入生产，投入品被交易为货币，消费者把禀赋卖给企业作为投入品，以获得货币；所有消费都发生在时期2，消费者用在时期1出售禀赋给企业获取的货币来购买企业的产出。不一定能得到角点解，但确保 x = w 的一个充分条件是：

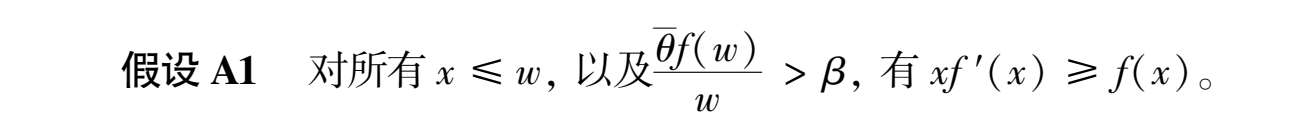
我们可以把这个结果设定为如下竞争均衡：企业在时期1放弃其持有的全部现金，以购买禀赋 w ，消费者则在时期2买下企业的全部产出 θf （ w ）。在这一均衡中，时期1产品的货币价格为 p ₁ = m/ w ，时期2产品的货币价格为 p ₂ （ θ ） =m /[ θf （ w ）]。给定这些价格，时期2货币的实际价值为：

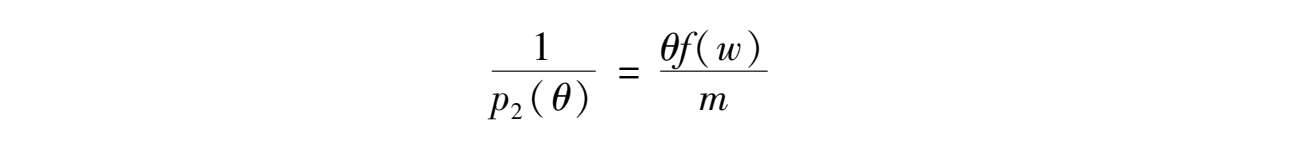
可以很直观地证明，在假设A1之下，代表性消费者的最佳选择是在时期1以价格 p ₁ 出售自己的全部禀赋，代表性企业的最佳选择是在时期2以价格 p ₂ （ θ ）出售自己的全部产出。事实上，如果考虑到代表性消费者有可能在时期1只出售部分资源禀赋 x < w ，并消费掉剩余部分 c ₁ = w - x ，那么其生命周期的预期回报将由如下公式给定：

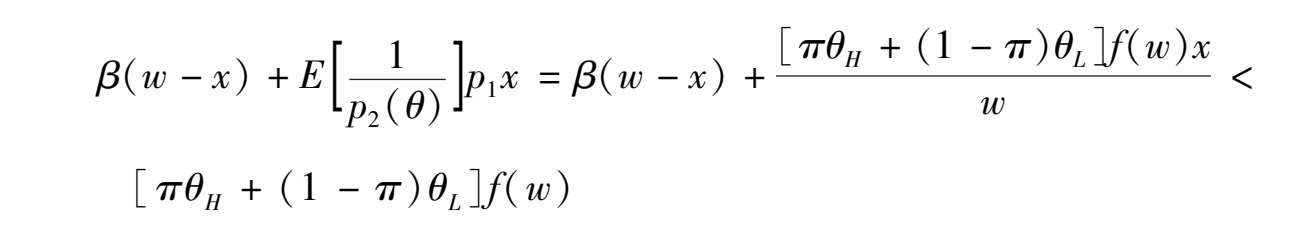
其中的不等式根据假设A1即可得出。

与之类似，如果代表性企业在时期1保留部分现金，只购买 x <w 的投入品，则它在时期2将只能生产和出售不多于[ πθ H + （1 -π ） θ L ] f （ x ）的产出，企业在时期2末期的全部现金存量将等于：

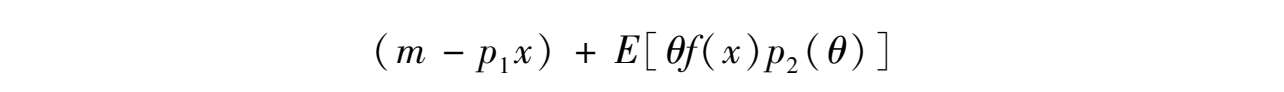
对于任何 x ≤ w ，企业在边际上可以持有 p ₁ 的货币，或者选择多购买1单位投入品，并以预期价格 E [ p ₂ （ θ ）]多出售 单位的产出。若满足以下条件，企业的最佳选择将是把持有的全部货币用于购买投入品：

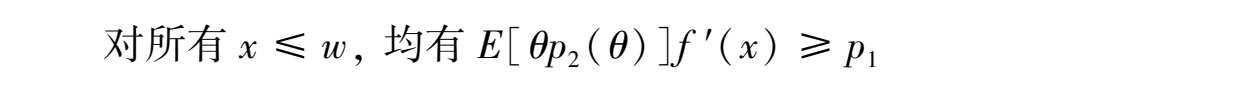
或者代入 p ₂ （ θ ）和 p ₁ ，在假设A1之下，对所有 x ≤ w ，均满足：

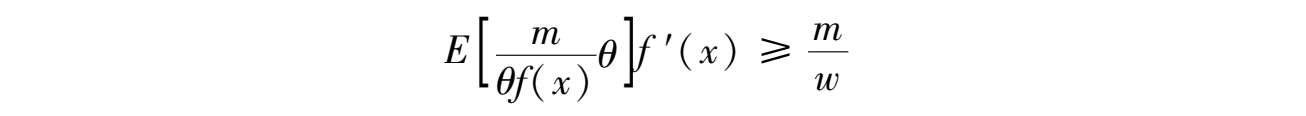
总而言之，在假设A1之下，该经济体的均衡状态是企业在时期1用货币量 m 从消费者手里买下全部投入品 w ，而消费者则在时期2用货币量 m 买下企业提供给市场的全部产出 θf （ w ）。

传统货币数量论在这一经济中依然成立，例如把经济中的货币存量增加1倍，将使时期1的产品价格翻番，并使时期2的货币价值减半。