2.适用于国家的莫迪利亚尼-米勒定理

现代公司金融理论的基础是莫迪利亚尼-米勒定理，它认为在没有税收的完全竞争的金融市场中，企业的财务价值与融资方式无关。企业的投资可以完全来自股票融资或完全来自债务融资，其净现值（企业的总现值减去其投资成本）将维持不变。为支持投资而选择的其他任何债务融资与股票融资的组合也不会影响企业的净现值。这一定理背后的基本理由是，价值创造取决于实际投资活动产生的新现金流，而融资方式只会影响新创造的现金流如何在股东与债权人之间分配。但是，当金融市场出现缺陷，或者因为利息支出能够从公司应税收入中扣除而让债务融资拥有税收优势的时候，企业资本结构的无关性也就不再成立。

针对主权国家可以提出类似的定理。事实上，传统货币数量论正是这一无关性定理的推论。为得出这一定理，我们必须考虑国家在时期0如何为基础设施投资筹集资金。某个国家通过在时期0投资 k >0（这些投资可以提高企业的生产率），企业在时期2的产出会因此增加 Q （ k ）倍，我们假设 Q （0） = 1, Q′ > 0以及 Q″ < 0。为了让问题更有意思，我们再假设这是一项净现值为正的投资：

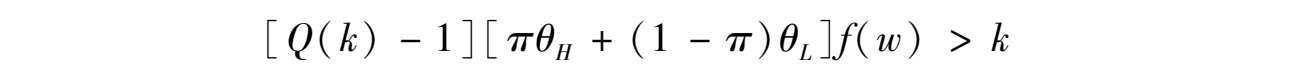
为简化表述，我们令 Q （ k ） f （ w ） = Ω（ k , w ）。另外，如果在时期0该国的禀赋为 w 且实施了投资 k 的时候，对Ω代表其产出水平没有疑义，我们将不考虑Ω对 k 和 w 的依赖。

这个国家将按照标准化为1的世界市场价格，从国际资本市场上筹集数量为 k 的资金。根据开放经济研究中的一般假设，我们把世界利率水平确定为0，相当于让世界市场的资本价格为1。对于这些资本，该国可以通过在时期0增发数量为 δ ₀ m 的货币来支付，或者承诺用时期2的产出来偿还。

我们的分析首先提出一个简化假设：该国可以发行无违约的外币债务。之后再考虑主权债务违约的可能性及其各种严重后果，这些将在我们的理论中起到核心作用。为确保该国不会对债务违约，我们必须要求它即使在最低的生产率水平下也有足够的资源来偿债。可以实现这种情形的一个充分条件是：

假设A2 θ L Ω> k 。

在竞争性的全球资本市场中（世界市场的利率水平标准化为0），这个国家可以承诺在时期2予以偿还，从而在时期0筹集到资金 k 。当不存在债务违约时，这一承诺的还款额将等于债务的面值。所以在假设A2下，即使生产率处于最低水平 θ = θ L ，该国的产出也会超出其债务负担 k ——我们假定该国能够承诺，在有能力偿债时就不会违约。

根据上述假设，对国家适用的莫迪利亚尼-米勒定理将得以成立：

当国际资本市场处于完全竞争状态时，基础设施投资的净现值与某个国家为投资项目选择的融资方式无关。为了支付 k ，它可以选择发行货币、发行外币债务或者债务与货币的任何组合。这一定理得以成立的基本原因如下所述。无论某个国家在时期0是通过发行货币还是债务来筹集资金 k ，它都必须承诺在时期2偿还至少为 k 的金额。这就意味着在时期2，无论基础设施投资的资金是来自货币还是债务，都至少有 k 的产出将归属基础设施的（外国）投资人，剩下的产出才归属本国居民。如果国际资本市场是完全竞争性的（莫迪利亚尼-米勒定理的基本假设之一），则无论是通过货币还是债务融资，都不需要向投资人承诺偿还多于 k 的最终产出。

可以很直观地证明（Bolton and Huang, 2018），当一个国家完全通过增加货币供给来筹集投资资金 k 的时候，基础货币的总增量为 δ 0 m ，其中：

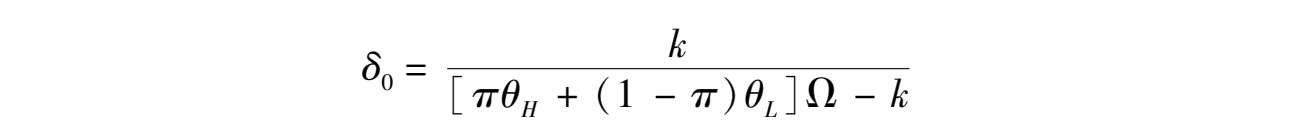
这里的 δ ₀ 由一个无关条件来确定。在用货币融资的时候，竞争性的外国投资人会要求 δ ₀ m = E [ p ₂ （ θ ）] k ，以期望在时期2能够把资金 k 买回来。

换句话说，货币供给在时期0的增幅取决于资本支出 k 与扣除投资支出的预期净产出 的比值。对 δ ₀ 的这个表述意味着货币供给的一个简单法则，它与货币主义者的建议类似，即货币供给的增长应该与实际产出的增长成比例。如本书第1章所述，关于货币增长的货币主义理论并未指出这一比例常数应该是多少，很大程度上是因为它没有考虑货币进入经济的具体方式以及货币可以购买什么东西。我们的分析则指出了货币进入经济的一种重要渠道：通过资本支出来提高国家的生产率水平。正是通过聚焦这一渠道，我们可以得出一个简单的经验法则：基础货币的增长应该与资本支出的正净现值（扣除资本成本后）同GDP之比成正比。

我们的模型得出的另一个有趣结论是，两种融资模式之下的绝对价格水平是相同的，尽管发行货币这一融资方式事实上会使经济中有更多的货币数量。这是因为基础货币的增长是为了支持预期产出的增加。

货币增长速度由投资机会决定。相应地，有更大增长潜力、更多有利可图的投资机会的经济应该有更高速的货币增长。

前文提到，适用于国家的莫迪利亚尼-米勒定理的一个推论是，传统货币数量论得以成立。这点能够从我们的简化理论框架中很直观地得出。由于 p ₁ 和 E [ p ₂ ]是 m 的线性函数， δ ₀ 与 m 无关，那么经济中的货币存量翻番会直接导致时期1的产品价格翻番，时期2的货币价值减半，同时要求该国在时期0发行数量为2 δ ₀ m 的货币。适用于国家的莫迪利亚尼-米勒定理与传统货币数量论之间的联系源自如下事实：货币既是价值储存手段，又是交易媒介。

公司金融理论的一个基本信条以及适用于国家的莫迪利亚尼-米勒定理的一个推论是，股票分拆（把一单位股份分为两个或更多单位）本身不会改变企业的市场价值。企业会产出同样的现金流和同样的净现值，改变的只是把这些价值拆分为多少个数量的单位。但事实上，股票拆分经常伴随着企业市值的变化，已有少量研究文献解释了这种现象的原因。一种常见说法是，企业会在股票拆分的同时做一些改变现金流的其他事情。另一种说法是，由于股东们可以用更小的单位来交易股票，二级市场的流动性会提高。一个国家的货币面值变化可以被理解为与企业股票拆分类似的现象，它对经济体的影响应该是中性的，正如股票拆分对企业市值的影响。这是理解货币数量论的另一种思路。除非货币购买的东西改变了国家的生产率，否则唯一受影响的只有价格水平。

对这里描述的经济还有一个有意思的发现：由于商品在时期1被用于改进生产率的投资，货币的价值会随时间而提升。然而，由于世界市场利率水平为0，时期1和时期2的最优货币数量是不确定的（假设发行货币没有交易成本）。

我们2018年曾对适用于国家的莫迪利亚尼-米勒定理做了严格证明。该无关性结论基于巴罗（Barro, 1974）提出的著名的李嘉图等价定理，认为在完全竞争的经济中，政府的债务发行本身不会创造任何价值。政府发行的任何债务都必须在未来某个时点偿还，这就要求未来有更多的税收收入，而如果预期到这些场景，那么今天发行债务带来的减税效果就会被因为预见偿还债务所需的未来增税而增加的储蓄抵消。与公司资本结构的无关性一样，完美的资本市场排除了通过纯粹的财务操作来创造价值的可能性；在完美的国际资本市场环境中，国家也无法仅通过债务与货币之间的转换来创造价值。

所有这些都表明，关于债务融资比发行货币更好（反之亦然）的任何观点，乃至关于最优法定货币供给的任何理论，都必须以国际资本市场的某些关键缺陷作为基础。我们下面将识别和讨论这些缺陷。