2 循环中包含的循环打开新维度
回想一下在读小学时,你第一次学习如何在纸上画一个三维立方体。你首先画两个部分重叠的正方形,然后把两个正方形对应的四角连起来。纸的表面虽然是平的,但是你的大脑看到了立方体的线条,情不自禁地想象纸面上出现了更多的空间。乍一看,这似乎是不可能的,因为没有任何可供增加空间的新点位,你看到的只是视错觉。不过,你可以这样思考:从技术层面上来说,绘制的立方体为你提供了更多的空间——因为你现在可以在这个立方体中放置点,然后进入一个全新的维度。要想理解这一点,你首先需要激活你的想象力:想想在绘制立方体之前,你在这张纸上找不到任何大小的三维空间,但取决于你的绘制方法,你可以让这个立方体比纸面更大。
让我们用不同的方法将这个过程重复一遍,数学家们把它作为开启第四维度的大门。首先画一个点,这表示零维。

然后将这一点在空间中展开,将两点相连,你会得到一条线,这表示一维。

然后将这条线在空间中展开,将四个顶点相连,你会得到一个平面,这表示二维。

然后将这个平面在空间中展开,将八个顶点相连,你会得到你所知的立方体,这表示三维。

那么,你觉得你应该如何描述第四维呢?没错!将这个立方体在空间中展开,将这十六个顶点相连,你会得到一个超立方体,这表示四维。
每次维度增加时,我都希望你能体会到什么是典型的指数移动。例如,当我们从一维移动到二维,将一条10毫米长的线投射为边长10毫米的正方形时,这个新空间就覆盖了100平方毫米的面积。这在空间大小上是一个很大的跳跃,而当我们移动到三维空间时,空间会更大——这不仅仅是大小的增长,还是超维的增长。
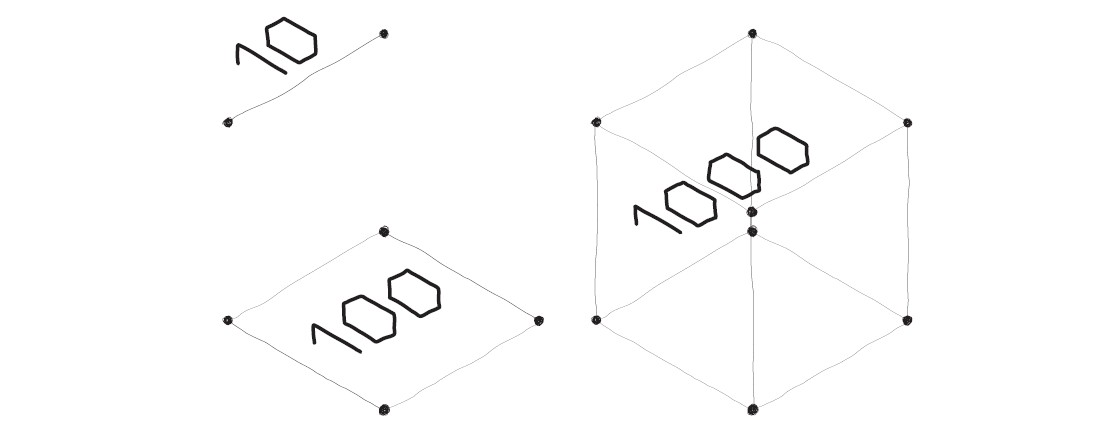
从100平方毫米到1,000立方毫米的三维空间。每一次维度变化时,我们在空间中的增长都是指数级的。我知道这些很抽象,虽然我很想为你介绍一个易于理解的物理比喻,但我只想到一个看不见的:循环。你准备好了吗?
让我们先来想想如何定义“十年”,想想每年是如何被划分为12个月的。我们通过循环来遍历“十年”:
for ( year = 1; year <= 10; year = year+1 ) { }
这段代码从year = 1开始,每次递增1,到year大于10时终止。它目前没有做任何重要的事情,因为它应用于一个内部没有任何东西的代码块。{ }可以被视为一个紧紧的“拥抱”,其内部的代码就像一个整体那样抱在一起。让我们看看运行结果。
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
接下来,让我们把第一段代码中的year替换为month,设定其终止于12而不是10,以循环一年中的12个月:
for ( month = 1; month <= 12; month = month+1 ) { }
运行结果如下。
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
现在,让我们把月循环放到年循环中。
for ( year = 1; year <= 10; year = year+1 ) {
for ( month = 1; month <= 12; month = month+1 ) {
}
}
将发生的情况是一年将循环10次,而一个月也将在每一年中循环12次。如果把结果列出来,它会是这样的:
1.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
2.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
3.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
4.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
5.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
6.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
7.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
8.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
9.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
10.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
你注意到那种感觉了吗?通过简单地将一个循环放在另一个循环中,让你感觉不自然的事情就会发生。现在,如果假设每个月都是30天——为了让这个例子更容易理解,你可以使用以下代码:
for ( day = 1; day <= 30; day = day+1 ) { }
让我们把结果列出来:
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14.15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25.26. 27. 28. 29. 30.
你能想象,如果你把这个循环放到月循环中会发生什么吗?
for( year = 1; year <= 10; year = year+1 ) {
for( month = 1; month <= 12; month = month+1 ) {
for( day = 1; day <= 30; day = day+1 ) { }
}
}
我不想把所有纸张都浪费在追踪这个案例上,但如果你想自己试试看,你可以这样开始:
1.
1.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21.22. 23. 24. 25. 26. 27. 28. 29. 30.
2.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
3.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
……
然后数完3,600个数字的其他部分,这些数字是你在三维空间中通过追踪10年、每年中的12个月、每月中的30天生成的。这很像把直线延伸成一个平面,然后把这个平面延伸成一个立方体。所有这一切的实际意义,是当一个循环进入另一个循环的内部时,它就像电火花,让紧紧拥抱的{}中的任何内容全速运行。
任何内容都可以置于{}中。例如,假设你在网上某个地方租用了10台计算机,你可以轻松通过循环所有机器让它们来完成你的任务。
for( machine = 1; machine <= 10; machine = machine+1 ) {
for( year = 1; year <= 10; year = year+1 ) {
for( month = 1; month <= 12; month = month+1 ) {
for( day = 1; day <= 30; day = day+1 ){ }
}
}
}
或者你可以倒置这个逻辑,在10年时间里的每一天在这10台机器上做一些事情:
for( year = 1; year <= 10; year = year+1 ) {
for( month = 1; month <= 12; month = month+1) {
for( day = 1; day <= 30; day = day+1 ) {
for( machine = 1; machine <=10; machine = machine+1 ) { }
}
}
}
你也许会有以下想法:
·没有什么可以阻止你把year <= 10改成year <= 100,000。
·通过这种方式,你可以一直数到时、分和秒。
·如果我们租几千台机器,我们可以轻松把机器总数从10改成任何你能访问的机器的总数。
每一次循环的嵌套都引入了一个新的维度,就像我们把一个点变成一条直线,然后把一条线变成一个平面,再把一个平面变成一个立方体。随着每一个连续的“被拥抱”或“嵌套”的循环,另一个维度的可能性出现了。在嵌套发生之前不存在的空间突然出现了,调整每个维度的开始和结束限制会增大或减小增加的空间。简而言之,这是一种打开远远超出我们面前或周围物理尺度的空间的方法,这个空间可以大到整个社区乃至整个城市。每个维度可以延伸的距离没有限制,而且通过进一步嵌套循环可以创造出多少个维度也没有限制。对生活在模拟世界的我们来说,这应该很不自然,但这只是计算宇宙中的再自然不过的一天。


