2.3 数据处理:使用Python分析金融数据
下面将给出一个关于如何处理2.2.2小节中的下载数据的Python处理步骤。我们需要使用NumPy和Pandas库来分析这些数据,因为它们非常适合处理时间序列数据。

然后,我们对数据进行如下处理。


其中,提到的几个指标如下。
(1)普通收益率(也叫作简单收益率):指从一天到下一天价格变动的百分比。
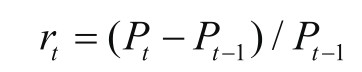
其中,r t 为在时间t的普通收益率,P t 为在时间t的价格,P t−1 为在时间t−1的价格。
(2)对数收益率:价格相对变动的另一种衡量方式,对于小的变动,它和普通收益率相近。但是,对数收益率有一些数学属性使它在金融分析中更为有用。例如,多个时间段的对数收益率可以直接相加。
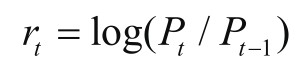
其中,r t 为在时间t的普通收益率,P t 为在时间t的价格,P t−1 为在时间t−1的价格。
(3)平均每日收益率:所有每日收益率的平均值,可以用来衡量资产的平均每日收益。
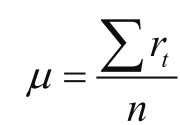
其中,µ为平均每日收益率;r t 为在时间t的收益率;∑为求和符号,表示对所有的t(从1到n)进行求和;n为观察期的天数。
(4)平均每日波动率:所有每日收益率的标准差,可以用来衡量资产价格变动的不确定性或风险。
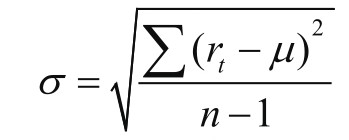
其中,σ为平均每日波动率;r t 为在时间t的收益率;µ为平均每日收益率;∑为求和符号,表示对所有的t(从1到n)进行求和;n为观察期的天数。
(5)年化收益率:将平均每日收益率换算为年化值,使我们可以更好地比较不同的投资。
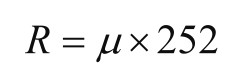
其中,R为年化收益率,µ为平均每日收益率,252为一年的交易日数。
(6)年化波动率:将平均每日波动率换算为年化值,用来衡量资产一年的价格变动风险。
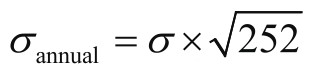
其中,σ annual 为年化波动率,σ为平均每日波动率,252为一年的交易日数。
图2.5所示为通过运行Python得到的上述几个金融指标的数值结果。
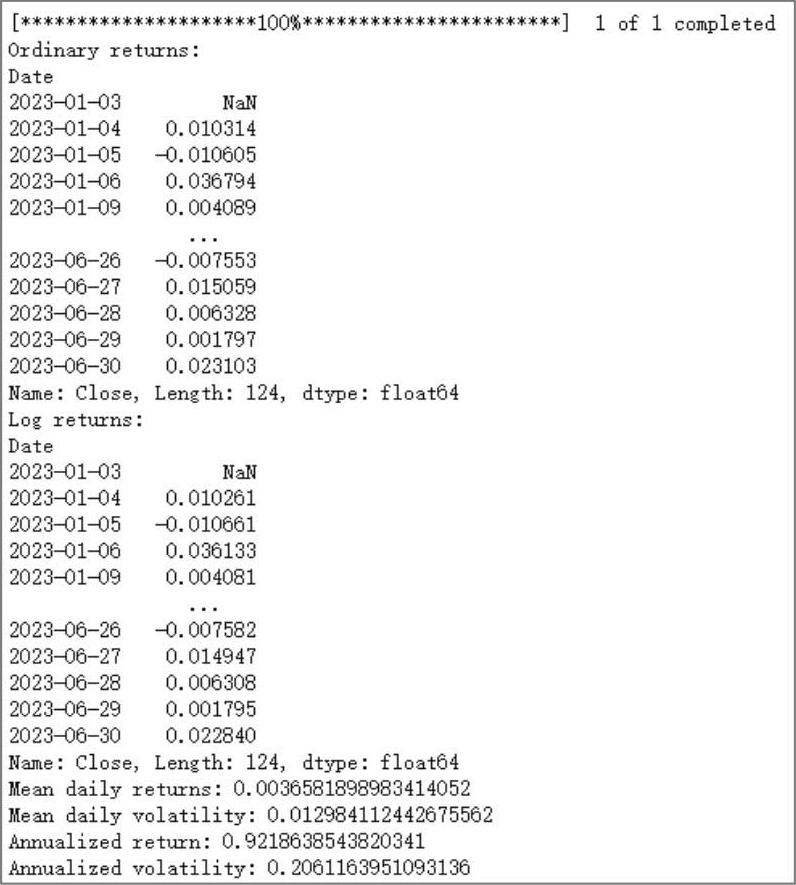
图2.5 股票普通收益率、对数收益率及年化波动率
从图2.5中,我们不仅可以看到苹果公司每日的普通收益率和对数收益率,同时还计算出了该股票每天的平均收益率约为0.3658%,每天的平均波动率(无论上涨或下跌)约为1.2984%,如果这只股票的价格能持续其当前的日均收益率,那么其一年的收益率约为92.1864%;如果这只股票的价格能持续其当前的日均波动率,那么其一年的波动率约为20.6116%。
2.3.1 重新采样
在处理时间序列数据,如股票价格时,重新采样(Resampling)是一个常见且重要的步骤。重新采样是改变数据的时间频率的过程,比如,你可能有一些每日收盘价数据,你可以将其重新采样为每周、每月、每季度甚至每年的数据。换句话说,你可以将高频数据降采样为低频数据(如从每日数据到每月数据),或者将低频数据升采样为高频数据(如从每月数据到每日数据)。
Python的Pandas库提供了一种方便的方法来进行重新采样,使用的是resample()函数。这个函数可以用各种各样的频率参数,且可以自定义重新采样的方法。
让我们基于之前的例子,使用苹果公司的收盘价数据来演示重新采样。

得到的结果如图2.6所示。
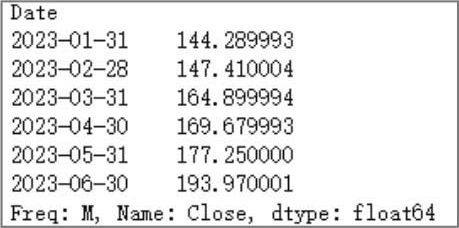
图2.6 重新采样结果
在这个例子中,我们使用resample('M')函数将每日数据重新采样为每月数据,'M'代表月份。然后我们使用last()函数,将每月的最后一个交易日的收盘价作为该月的收盘价。从图2.6中可以看到,重新采样的结果为月度数据。这只是其中一种选择,实际上,你可以使用任何适合你需求的函数,如mean()(平均)、first()(第一天)、max()(最大值)、min()(最小值)等。
通过这些函数,我们可以观察到每个月的平均收盘价、第一个交易日的收盘价、最高的收盘价,以及最低的收盘价。
当我们降低时间序列数据的频率(比如,从每日数据到每月数据)时,我们需要决定如何处理在一个时间单元(比如,一个月)内的多个观测值。这4个函数都是常见的处理方法,它们从不同的角度提供了对数据的概述。
选择哪种处理方法取决于你的具体需求。例如,如果你关心的是价格的总体趋势,那么可能会选择使用mean()函数;如果你关心的是每月的最高价或最低价,那么可以选择使用max()函数或min()函数。
需要注意的是,重新采样可能会导致信息的丢失(在降采样的情况下)或信息的插入(在升采样的情况下),所以在实际操作中应该根据具体需求选择合适的采样频率和方法。
2.3.2 滚动统计
滚动统计(Rolling Statistics)是一种常见的时间序列数据分析手段,它对固定大小的滑动窗口进行计算,以生成一系列的统计值,如滚动平均、滚动标准差等。这种方法可以帮助我们更好地理解时间序列数据的局部特性和变化趋势。
Python的Pandas库提供了方便的方法来进行滚动统计,主要使用的是rolling()函数。rolling()函数会创建一个滑动窗口,我们可以在这个窗口上进行各种统计运算。
让我们基于之前的例子,使用苹果公司的收盘价数据来演示滚动统计。


在这个例子中,我们使用rolling(window=10)函数创建了一个大小为10的滑动窗口。然后我们在这个窗口上分别计算了滚动平均价格(mean())和滚动标准差(std())。这些统计值可以帮助我们了解价格的短期变化趋势和波动情况。
同样,你可以根据需求使用任何适合的窗口大小和统计函数。比如,如果你想看更长期的趋势,可以选择更大的窗口;如果你想看价格的中位数、最高值或最低值,可以使用median()、max()或min()函数。

需要注意的是,滚动统计只考虑了时间窗口内的数据,而忽视了窗口之外的信息。因此,滚动统计是一种对数据局部特性的描述,而不是全局特性。
如果要从第10天开始绘制其趋势线,可以使用如下代码。

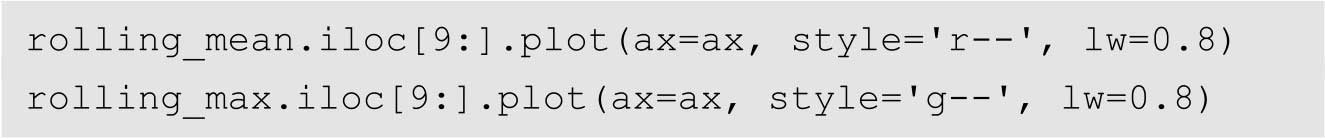
得到的结果如图2.7所示。
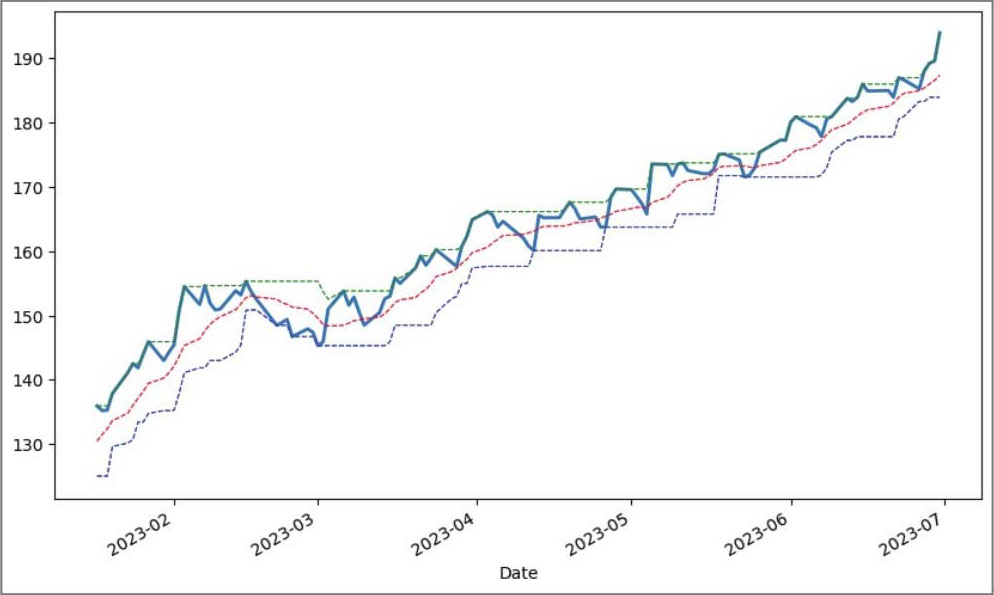
图2.7 苹果公司的滚动统计示例
从图2.7中可以直观地看到近200天的股票价格及该期间的滚动平均值、最大值和最小值的变化,有助于进行更深入的数据分析和理解。
滚动统计是股票技术分析的主要工具之一,基于技术分析的交易策略有几十年的历史,这种策略使用两条简单移动平均线(Simple Moving Average, SMA)。这个策略的思想是,当短期SMA位于长期SMA之上时,交易者应该对股票(或一般的金融工具)进行买入,而当相反情况发生时,应该进行卖出。通常只有在满足窗口参数规定的数据量足够多时,才会计算滚动统计数据。
这里我们以短期为5的滑动窗口(一周),长期为20的滑动窗口为例,代码如下。

这里提到了两种类型的SMA:5日SMA和20日SMA。
(1)5日SMA:作为一个短期简单移动平均线,5日SMA确实为我们捕获了股票的短期动态。它迅速反映了最近的价格变化,这也意味着它更容易受到日常价格波动的影响。在一个明确的趋势中,5日SMA通常会密切跟随股价。
(2)20日SMA:20日SMA为我们提供了对股票中期行为的见解。由于它涵盖了更长的时间框架,它更能够反映出股票的真实趋势,并过滤掉一些不重要的价格波动。
交易策略的核心观点是,当5日SMA从下方穿过20日SMA(短期平均价格超过长期平均价格)时,这是买入信号,说明可能会有一个上升趋势。相反,当5日SMA从上方穿过20日SMA时,这是卖出信号,说明可能会有一个下降趋势。这两条简单移动平均线经常一起使用,以确定所谓的“金叉”和“死叉”。简而言之,金叉是一个买入信号,而死叉是一个卖出信号。但在实践中,交易策略并不总是那么简单,因为还需要考虑其他因素,如交易成本、其他技术指标和市场情况。我们把两条SMA展示在图2.8中。
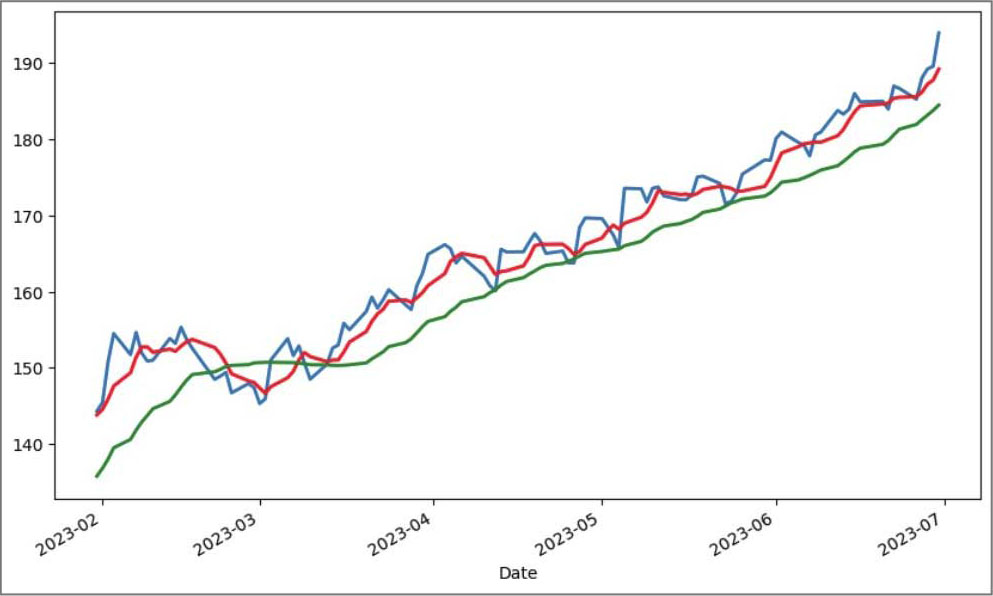
图2.8 苹果公司的5日SMA和20日SMA
从图2.8中可以看到,除3月左右,该股票呈下降趋势以外,其余时间几乎都处于上升趋势。然而,需要注意的是,任何技术分析工具都不能百分之百地准确预测市场行情。在实际操作中,投资者通常会结合其他的技术分析工具和基本面分析来做出投资决策。


