1.1 引言：量化金融与算法交易简介

量化金融与算法交易在过去几十年中对金融市场产生了巨大的影响。从投资组合管理到风险控制，再到订单执行，它们已经在现代金融实践中扮演了核心角色。本节旨在为读者提供一个全面的概述，涵盖量化金融和算法交易的关键概念、发展历程和应用模型。无论你是刚刚开始探索这个领域，还是已经拥有深厚的经验和知识，你都会在这里找到有价值的信息。

1.1.1 量化金融及其发展历史

量化金融就是使用数学模型来帮助我们理解和预测金融市场的行为。这听起来可能很抽象，但我们可以通过它的发展历史来了解它是如何为投资者解决实际问题的。

在20世纪早期，尽管金融市场已经存在了一段时间，但大多数的交易决策都是基于直觉和经验。这种方法虽然有时有效，但也容易受到情绪的影响，导致非理性的决策。于是，一些先驱者开始尝试使用数学和统计方法来帮助他们更好地理解市场。

例如，1952年，Harry Markowitz为了解决如何将资金分配到不同的投资中以达到最佳的风险收益比，提出了现代投资组合理论（Modern Portfolio Theory, MPT）。简而言之，他建议不要将所有的资金投入同一资产中，而是要分散投资，以减少风险。这种思想听起来似乎不是很直观，但Markowitz给出了一个明确的数学模型来描述这一点。

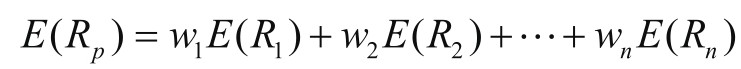
其中，R _p 为投资组合的预期收益，w _n 为资产n在投资组合中的权重，E(R _n )为资产n的预期收益。投资组合的方差（一个风险的度量）计算公式为：

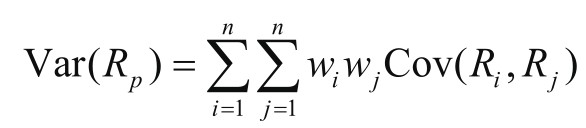
其中，Cov(R _i , R _j )为资产i和资产j之间的协方差，它衡量的是两个资产价格变化之间的关系。如果两个资产的价格通常朝相反的方向移动（一个上涨时另一个下跌），它们的协方差会是负数，这意味着组合这两个资产可以减少投资组合的整体风险。对于只有两个资产的投资组合，协方差是关键。但在现实中，投资组合通常包含许多资产，这时协方差矩阵就起到了关键作用，这个矩阵包含了组合中所有资产之间的协方差。

进入20世纪60年代，William Sharpe带来了资本资产定价模型（Capital Asset Pricing Model, CAPM），这是一个帮助投资者理解资产收益率与市场整体收益率之间关系的工具。CAPM的核心公式为：

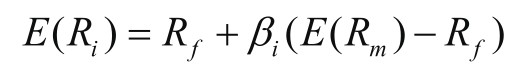
其中，E(R _i )为资产i的预期收益；R _f 为无风险利率，通常可以用短期政府债券的收益率作为参考；E(R _m )为市场的预期收益，可以用一个广泛的市场指数（如S&P 500）的预期收益率作为参考。β _i 为资产i的Beta系数，它衡量的是资产i的系统风险。简单来说，如果β 1 _i =，那么资产i的预期收益将完全与市场同步；如果β 1 _i >，则资产i的收益将比市场更加波动；如果β 1 _i <，则资产i的收益将相对市场更加稳定。这为投资者提供了一个评估资产的风险相对于其潜在收益的方式。Beta系数可以通过以下公式计算。

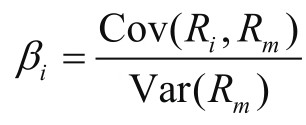
其中，Cov(R _i , R _m )为资产i与市场收益之间的协方差，Var(R _m )为市场收益的方差。

到了20世纪70年代，Fischer Black和Myron Scholes提出了著名的Black-Scholes模型，为期权定价带来了一场革命。期权交易在当时非常流行，但如何公正地为期权定价却是一个大难题。Black和Scholes为此提供了一个解决方案，他们的模型可以基于一系列的变量来预测期权的价值，如资产的当前价格、期权的到期日期和预期的市场波动率。

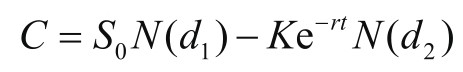
其中，C为看涨期权价值，S ₀ 为资产当前价格，K为期权执行价格，e为自然对数的基数，N为正态分布函数，d ₁ 和d ₂ 为公式中的变量。

Black-Scholes模型是期权定价理论中的里程碑。由于这个模型的重要性和影响，Myron Scholes和Robert C. Merton（他进一步发展了该模型）在1997年被授予诺贝尔经济学奖。值得注意的是，尽管Fischer Black是该模型的共同创作者，但由于他在1995年去世，因此没有与Scholes和Merton一同获得奖项。诺贝尔奖通常不授予已故的候选人。

Black-Scholes模型为期权和其他衍生品的公平定价提供了一个明确的数学公式。这一模型特别突出，因为在那个时候，衍生品市场还处于发展初期，缺乏一个统一的定价方法。此模型提供了一个系统性的方式来估计一个期权的“公平”价格，从而使交易者、投资者和风险管理者都能在一个公认的框架下操作。

Black-Scholes模型的成功引发了衍生品市场的巨大增长，同时也促进了金融工程学科的发展。

随着时间的推移，量化金融不仅局限于理论研究，而且开始广泛应用于实际投资策略，特别是在对冲基金中。比如，到了20世纪80年代，量化金融开始广泛应用于实际投资，许多对冲基金开始使用量化策略来寻求Alpha收益。20世纪90年代以后，计算机技术的发展和数据获取的便利为量化金融提供了强大的支持，机器学习和大数据分析也开始在这个领域中发挥作用，帮助投资者更精确地预测市场的行为。

综上所述，量化金融不仅提供了对金融市场的深入理解，还为投资者带来了实用的工具和策略，帮助他们在复杂的市场环境中做出明智的决策。

1.1.2 当代量化金融

随着时间的推移，量化金融已经不仅仅是基于经典经济理论的模型，还包括了大量数据驱动的策略，如机器学习算法、神经网络等。因此，当我们在讨论当代量化金融时，通常可以将其分为两大类：Q-Quant（Risk-Neutral Probability Measure，风险中性概率测度）和P-Quant（Actual Probability Measure，真实概率测度）。Q-Quant和P-Quant的区别如表1.1所示。

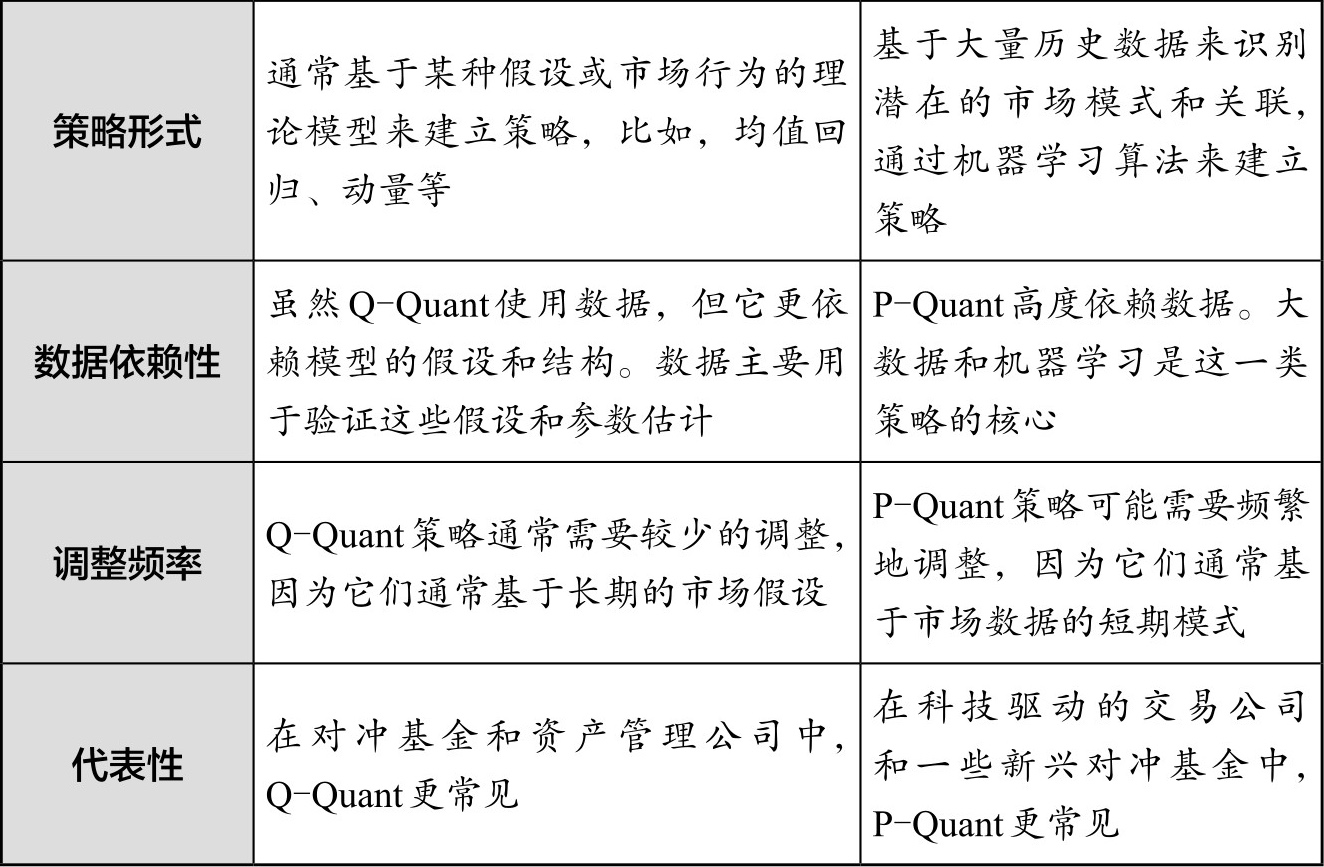
总的来说，Q-Quant倾向于使用基于理论的模型，而P-Quant则更注重使用数据来驱动交易决策。然而，这两种方法并不是相互排斥的。许多成功的量化策略结合了Q-Quant的理论洞察力和P-Quant的数据驱动能力。

1.1.3 算法交易概述

算法交易就是利用计算机算法自动执行交易策略的过程，它涵盖了从交易决策到订单执行的全过程。随着时间的推移，算法交易经历了从简单的订单执行优化到复杂策略应用的演变。

在20世纪80年代，算法交易刚刚崭露头角，当时它的主要目的是优化订单执行，以此减少交易成本。而这个时期的技术并不像现在那么先进，但它为算法交易的未来发展奠定了基础。

到了20世纪90年代，随着电子交易平台的普及和互联网技术的飞速发展，算法交易得到了迅速的推广。更为重要的是，交易策略也开始变得更为复杂，例如，统计套利等策略在这个时期受到了广泛的关注。

进入21世纪，特别是从2000年开始，算法交易不仅已经深入金融市场的每一个角落，而且开始与机器学习和人工智能等先进技术结合，为交易策略的研发和执行带来了前所未有的机会和挑战。这使得金融市场的运作变得更为智能化和高效。

在算法交易领域中，多种模型和策略得以应用，以满足不同的市场需求和投资目标。以下是一些核心的算法交易模型和策略的简要概述。

（1）TWAP（Time-Weighted Average Price，时间加权平均价格）:TWAP策略的核心思想是将较大的订单分解为多个较小的订单，这些小订单在指定的时间段内均匀地执行。其目的是在一段时间内尽可能接近平均价格，从而减少大宗交易对市场价格的影响。

（2）VWAP（Volume-Weighted Average Price，成交量加权平均价格）：与TWAP类似，VWAP策略考虑市场成交量的因素，目标是在成交量较大时执行更多的订单。数学上，VWAP定义为：

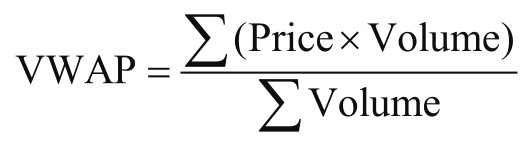
其中，价格（Price）和成交量（Volume）是在特定时间段内的。

（3）统计套利（Statistical Arbitrage）：统计套利策略依赖数学模型来识别和利用不同金融工具之间的价格偏差。这些偏差可能是由于市场无效率、信息滞后或其他相关因素造成的。

（4）趋势追踪（Trend Following）：趋势追踪策略利用技术分析方法来识别并跟随市场的趋势，无论是上升还是下降。这种策略通常依赖移动平均线、动量指标等工具。

（5）做市（Market Making）：做市策略通过在买入和卖出价格之间提供报价来赚取差价，为市场参与者提供流动性。

（6）机器学习算法（Machine Learning Algorithms）：这是一种相对较新的策略，它依赖机器学习技术来预测市场的运动并据此制定交易策略。与传统策略不同，机器学习算法策略可以自我调整并学习新的市场模式。

1.1.4 高频交易概述

在金融交易的世界中，高频交易已经确立了其独特的位置。这种交易方式以执行大量订单著称，并能在极短的时间内完成交易，具体到毫秒或微秒级别。这种现代交易方式的历史起源可以追溯到20世纪90年代末，那时，随着电子交易的崛起，高频交易初露锋芒。

进入21世纪后的10年，高频交易经历了爆炸式的增长，迅速崭露头角并成为市场的主要参与者。这样强劲的增长势头并不是偶然的，交易所提供的对高交易量的激励措施在其中发挥了重要作用，进一步推动了高频交易的盛行。

然而，转眼进入2010年，尽管高频交易依然在金融市场上活跃，其增长速度在某些市场却已经开始放缓。尤其是在美国的股票市场，高频交易的势头似乎不再像之前那般猛烈。不过，不可否认的是，高频交易仍然在当代金融交易中占有重要地位。

当我们深入探讨高频交易时，不可避免地要涉及一些具体的交易策略和技术。以下是一些在高频交易中常见的策略。

（1）市场套利：这种策略是基于市场之间的小的价格差异来获利的。例如，一个股票在两个不同的交易所上可能会有微小的价格差异。高频交易者会利用这些差异买低卖高，从中获利。

（2）市场做市：做市策略涉及为特定的证券提供买卖报价，以赚取买卖的差价。这种策略要求交易者要快速响应市场变化，以保持有竞争力的报价。

（3）统计套利：此策略利用数学模型来识别并利用金融工具之间的价格差异来获利。这种差异是基于历史数据和统计方法来确定的。

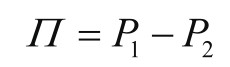
其中，Π为套利收益；P ₁ 为一个资产的价格，而P ₂ 为另一个相关资产的价格。

（4）买卖单薄冲击：在这个策略中，交易者会试图预测其他市场参与者的交易意图，并在这些交易执行之前采取行动。

（5）新闻算法交易：这是基于自动解析和解释新闻报道或财务报告的策略。一旦识别出对市场有影响的信息，算法会立即执行交易。

1.1.5 算法交易与高频交易的区别

算法交易和高频交易作为两种主要的计算机驱动的交易方式，它们都在近年来的金融领域中扮演了至关重要的角色。尽管它们在某些方面可能相似，但也存在显著的差异。为了更好地理解这两种交易方式，在表1.2中，我们详细比较了二者的特点和区别。

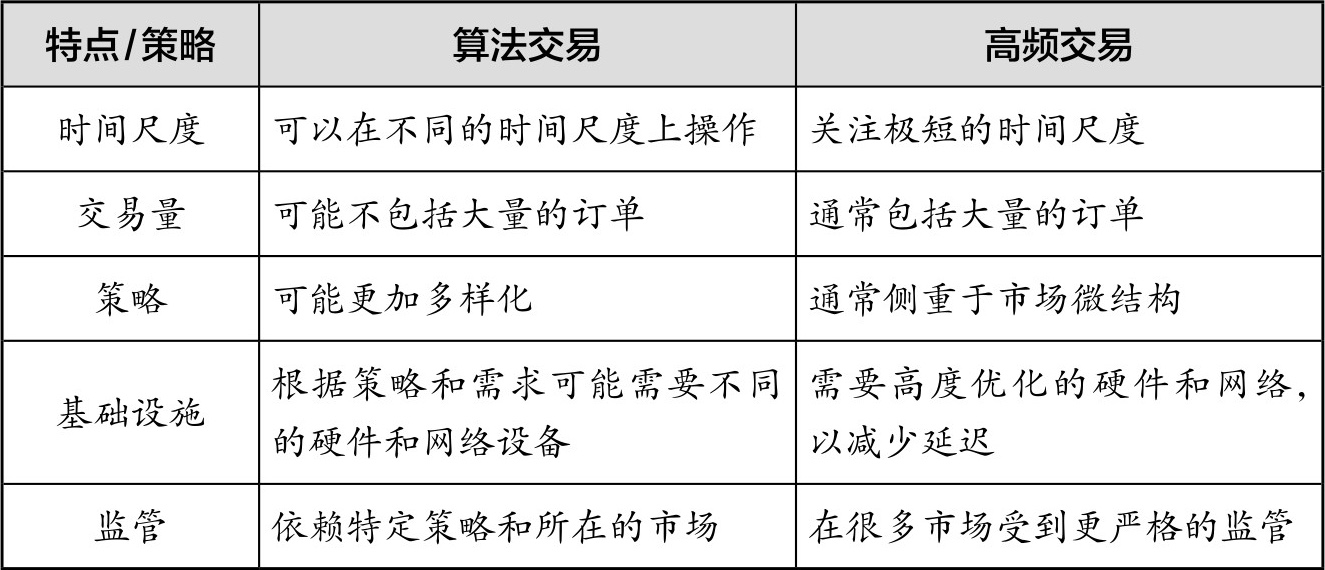
通过对比，我们可以看到算法交易和高频交易在多个维度上存在差异。高频交易主要聚焦在短时间内大量的交易活动，而算法交易则有更宽广的时间和策略范围。尽管高频交易是算法交易的一个子集，但由于其特有的特点和要求，往往被视为一个独特的领域。在进入这两个领域之前，理解它们之间的差异和相似之处是至关重要的。