第2章
天体力学:通向牛顿的路途
自然和自然规律隐没于黑夜中,上帝说:“让牛顿降生吧!”遂一片光明。
——亚历山大·波普(Alexander Pope,1688—1744年)
牛顿的运动定律和万有引力定律不仅优雅地解释了自古巴比伦时代以来的大量天文观测现象,还被证明是现代物理学发展的重要一步。
我们都非常熟悉某个版本的牛顿和苹果的故事,但要理解牛顿的成就,我们需要了解他当时所处学界的状况。而要做到这一点,我们需要看看人类对宇宙的看法——从托勒密时代(公元2世纪)到16世纪初,这些观点几乎没有发生任何变化——是如何在接下来的一个半世纪里,由4位性格迥异、非凡而迷人的科学家发展起来的。这4位科学家分别是尼古拉斯·哥白尼(Nicolaus Copernicus,波兰人)、约翰尼斯·开普勒(Johannes Kepler,德国人)、第谷·布拉赫(Tycho Brahe,丹麦人)和伽利略·伽利雷(Galileo Galilei,意大利人),正是他们的工作为牛顿在这一领域能有所建树奠定了基础,顺便还为优雅和不怎么优雅的科学提供了有趣案例。
我们首先要从天文学家、数学家和地理学家托勒密(Ptolemy)说起,因为他于亚历山大城写成的那部巨著中的宇宙观,在接下来约14个世纪里被人们普遍推崇。遵循古典希腊的传统,他认为,地球是一个位于宇宙中心的完美球体,太阳、月球和行星在同心圆轨道上绕着地球运动,它们的轨道直径依次增加:月球、水星、金星、太阳、火星、木星和土星。“固定星”——因为 相对于彼此的位置 没有变化而得名,被认为附着在一个以地球为中心旋转的最外层球体的内表面。
柏拉图和亚里士多德认为,所有天体都在以恒定的速度做完美的圆周运动,但这很难与观察到的行星运动相吻合。因为行星有时似乎会加速和减速,甚至停止或逆行。为了解释这些现象,后来的希腊天文学家以及托勒密本人提出几个巧妙的假说,我们在此不再探讨(注释 [1] 中有介绍)。
有趣的是,托勒密认为他最终设计的奇妙系统只是用于描述和预测行星运动的工具,包含39个(理论上的)轮子(如果算上带“固定星”的最外层球体,是40个)。在这方面,它相当成功,精确(仅需稍加修正)得足以让哥伦布和瓦斯科·达·伽马在15世纪用于航海导航。托勒密不认为它可以作为这些运动起因的可能指南。鉴于其神圣属性,人们不应指望天体遵循与凡间物体相同的运动规律。
直到充满怀疑精神的16世纪初,被大众接受了很长时间的托勒密系统开始受到天文学家的怀疑。托勒密曾考虑过一种可能性,即“固定星”的明显自转可能是地球自转的结果,但这被认为是荒谬的。尼古拉斯·哥白尼[他本来的姓氏是“Koppernigk”,后来被他改成了拉丁化的“Copernicus”(缘于其父亲是个铜商)]在著作
[2]
中重新考虑了这种可能性,并复兴了另一个希腊理论,即太阳是宇宙的中心。
 除了基本的“日心说”,哥白尼的工作并没有引人注目的优雅之处,也就是没有优雅的新理论、新实验或新证明。对行星运动的预测和对这些运动的观察之间的一致性仍然依赖于托勒密使用过的3种假说中的2种,而且最初使用“日心说”理论做出的预测误差更大。另外,还有一个更深层次的担忧,即哥白尼毫不怀疑地球在运动,但那种认为能够描述地球和所有行星运动的复杂理论机制与真实空间中的真实体系相对应的想法是站不住脚的。如果这个想法不成立,他面临的状况和托密勒的就非常接近了,即他能够描述和预测行星的运动,却不知道是什么原因导致它们运动,以及为什么它们以这样的方式运动。他不同意托勒密的安慰性观点,即不要期望天体与凡间物体遵循相同的运动规律。然而,通过复兴“日心说”,他在1543年弥留之际发表的伟大著作《天体运行论》被证明具有极其重要的意义。
除了基本的“日心说”,哥白尼的工作并没有引人注目的优雅之处,也就是没有优雅的新理论、新实验或新证明。对行星运动的预测和对这些运动的观察之间的一致性仍然依赖于托勒密使用过的3种假说中的2种,而且最初使用“日心说”理论做出的预测误差更大。另外,还有一个更深层次的担忧,即哥白尼毫不怀疑地球在运动,但那种认为能够描述地球和所有行星运动的复杂理论机制与真实空间中的真实体系相对应的想法是站不住脚的。如果这个想法不成立,他面临的状况和托密勒的就非常接近了,即他能够描述和预测行星的运动,却不知道是什么原因导致它们运动,以及为什么它们以这样的方式运动。他不同意托勒密的安慰性观点,即不要期望天体与凡间物体遵循相同的运动规律。然而,通过复兴“日心说”,他在1543年弥留之际发表的伟大著作《天体运行论》被证明具有极其重要的意义。

开普勒最终解决了哥白尼的许多难题,并对行星的运行轨道提供了更加清晰的见解。 [3] 1571年,在哥白尼出生近一个世纪后,开普勒出生在德国西南部一个名叫魏尔德尔斯坦特(Weil der Stadt)的小镇。他的祖父是那里的镇长;他的父亲后来抛妻弃子,险些被绞死;抚养他母亲的祖母被当作女巫烧死;他母亲在年老时也被指控使用巫术,并受到被烧死的警告。开普勒的一生可谓充满了灾祸,他一共有6个弟弟妹妹,其中3个在童年时就死了,还有1个患有癫痫病。开普勒本人是早产儿,小时候也经常生病,4岁时差点死于天花,而且视力还有缺陷——可能是天花造成的。成年后,他依然记得6岁时,也就是1577年,母亲带着他去看“大彗星”的情景。9岁时,他看了一次月食,并注意到月亮看起来相当红。
孩童时期的开普勒没有按时就学,但他后来从信奉新教的符腾堡公爵用没收自修道院的钱建立的高效学校系统(为“敬畏上帝”的贫苦男孩提供完整的奖学金)中获益良多。20岁时,他从图宾根大学毕业。他的兴趣一直是哲学、数学和天文学,但这时他又开始了为期3年的神学课程,目标是成为一名路德教牧师。当课程进行到一半时,有人向他提供了一个在格拉茨新教学校教授数学和天文学的职位,一番犹豫之后他接受了,从而避免了成为牧师的命运。
尽管开普勒是哥白尼体系的热心支持者,但他在格拉茨的早期工作带有浓厚的毕达哥拉斯学派神秘主义者的味道,追求天球中的和谐。有一天,在课堂上画图时,他突然意识到,如果你画一个圆的内接等边三角形,然后再为这个三角形画一个内切圆(见图10),那么这两个圆的相对大小看起来与土星和木星轨道的差不多。他继续思考:如果他在内圆内画一个内接正方形,再在正方形内画一个更小的内切圆,那么这个更小的圆的尺寸与火星轨道是否成比例?他能不能用五边形、六边形和七边形重复这一过程,得到地球、金星和水星的轨道?他做了这个实验,但没有成功。这时他又想到,由于宇宙是三维的,使用多边形非常愚蠢:“为什么要寻找二维图形来匹配空间轨道?我们应该寻找三维形体。”
[4]
那么,明显可使用的形体——因为正如古希腊人所证明的那样,它们是唯一完全对称的三维形体(每个形体都由相同的多边形面相接而成)——“柏拉图多面体”(见图11)。这样的多面体有5个:四面体(由4个等边三角形围成的三面金字塔)、立方体(由6个正方形围成)、八面体(由8个等边三角形围成)、十二面体(由12个五边形围成),以及二十面体(由20个等边三角形围成)。只有5个柏拉图多面体这一事实耐人寻味,因为6颗行星轨道
 之间只有5个空隙,所以如果每个多面体只使用1次,而且开普勒的假设是正确的,它就可以解释为什么只有6颗行星(包括地球)。
之间只有5个空隙,所以如果每个多面体只使用1次,而且开普勒的假设是正确的,它就可以解释为什么只有6颗行星(包括地球)。
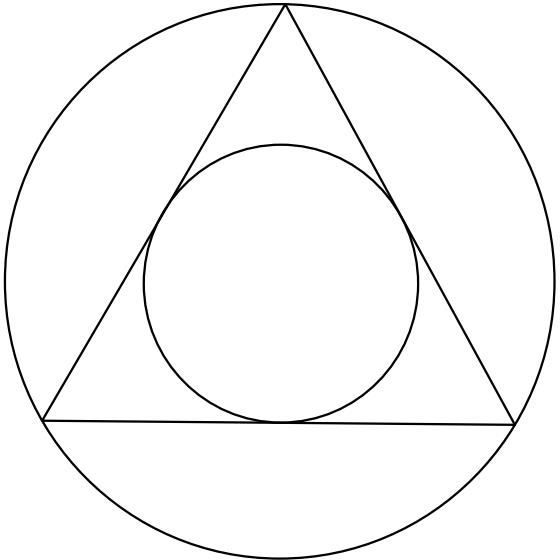
图10 开普勒的图显示,一个三角形外接圆和内切圆的相对大小,与土星和木星轨道的相对大小基本相同
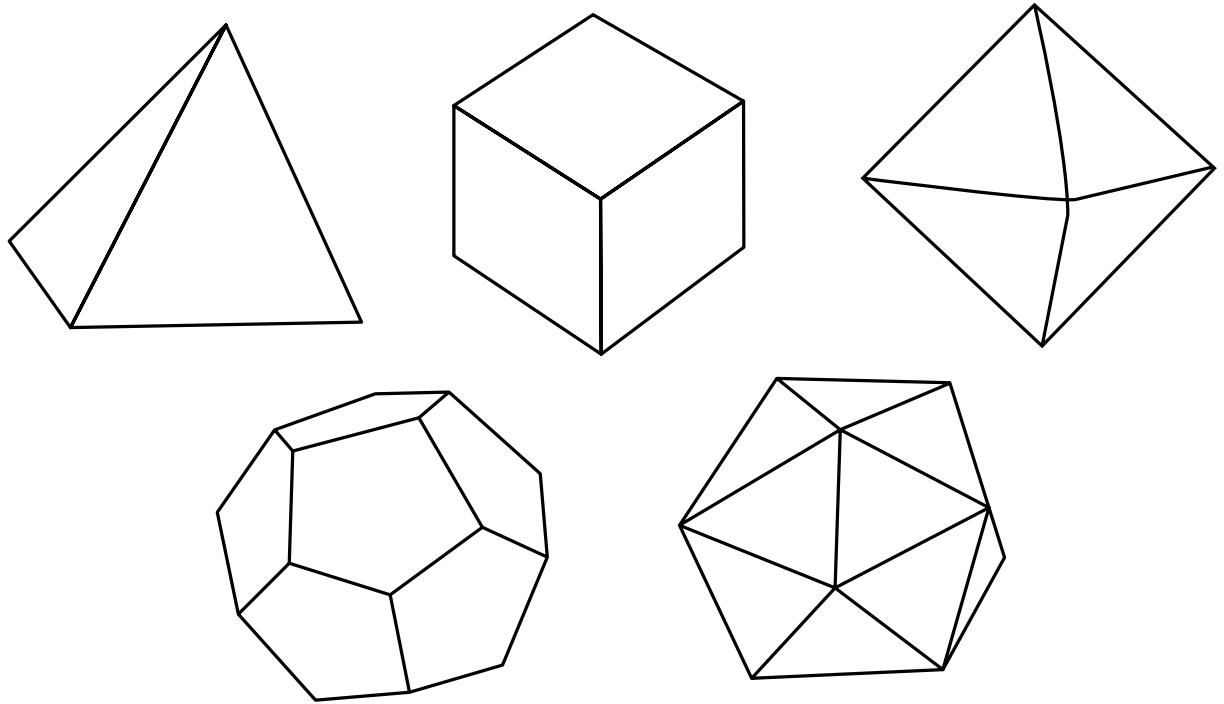
图11 5个“柏拉图多面体”
当开普勒研究能否将这5个多面体整齐地放入轨道间的空隙时,他发现,如果在土星和木星之间放入立方体,木星和火星之间放入四面体,火星和地球之间放入十二面体,地球和金星之间放入二十面体,金星和水星之间放入八面体,那么他的设想与现实之间匹配得就还算不错。他说:
我日日夜夜都在计算,看看我提出的命题是否符合哥白尼轨道,或者我的喜悦是否会随风而逝……几天内,一切各安其位。我看到一个又一个对称的多面体如此精确地嵌入适当的轨道之间。假如一个农夫问我,它们是被什么天界之钩固定住了吗,竟然不会掉下来?我很容易就能回答他。 [5]
这段引文来自开普勒的第一本著作——《宇宙的奥秘》(1597年)。这本书出版时,他刚满25岁,反映了他早年对自己得出结论的欣喜之情。但在该书的后半部分,他认识到自己的结论与哥白尼轨道的吻合程度并不像他最初想象得那么好,特别是对于水星和木星。他对轨道间空隙问题的优雅(多少有点神秘)解决方案开始显得可疑。这也是一次早期的提醒:即使是最优雅的解决方案也可能是错的。他需要的是更可靠的行星轨道数据,但这必须等第谷·布拉赫出现。与此同时,他还提出了一些不曾有人问过的有趣问题。他指出,从现有数据中可以看出,一颗行星离太阳越远,它沿其轨道移动的速度就越慢,而且他认为太阳:
对行星的驱动力在两者距离较近时较大,而(太阳)对外行星的作用力几乎已经枯竭,这是由于距离遥远,以及由此带来的力的减弱。 [6]
到16世纪末,开普勒因费迪南大公的反路德教政策而被迫离开格拉茨。1600年1月1日,他启程前往布拉格,接受了第谷·布拉赫长期以来的邀请,后者刚刚被波希米亚和匈牙利国王、神圣罗马帝国皇帝鲁道夫二世任命为 帝国数学家 。

比开普勒大24岁的第谷(人们通常称呼他的名而不是姓)是丹麦贵族,赫尔辛堡
 总督的儿子,由担任海军副司令的叔父抚养长大。
[7]
14岁那年,他观测到一次日偏食,大为惊讶。他惊讶的原因与其说是事件本身,不如说是该事件被预测到。为此,他立即购买了大量天文学书籍。2年后,他叔父急于消除天文学对第谷的影响,想让侄子接受适合贵族的教育,于是把他和一位合适的家庭教师一起送到莱比锡学习法律。自此,尽管年轻的第谷在白天学习法律,但到了晚上还是会秘密地进行天文观测。第二年(1563年),他观察到了土星和木星的会合(视位置的接近
总督的儿子,由担任海军副司令的叔父抚养长大。
[7]
14岁那年,他观测到一次日偏食,大为惊讶。他惊讶的原因与其说是事件本身,不如说是该事件被预测到。为此,他立即购买了大量天文学书籍。2年后,他叔父急于消除天文学对第谷的影响,想让侄子接受适合贵族的教育,于是把他和一位合适的家庭教师一起送到莱比锡学习法律。自此,尽管年轻的第谷在白天学习法律,但到了晚上还是会秘密地进行天文观测。第二年(1563年),他观察到了土星和木星的会合(视位置的接近
 ),并注意到事件发生的时间比13世纪《阿方索星表》预测的时间晚了1个月,比最近的《普鲁士星表》预测的时间晚了几天。
[8]
他后来说,这是他职业生涯的转折点。在莱比锡待了3年后,他回到哥本哈根。不久后,他的叔父去世,第谷从此自由地投身于天文学研究。
),并注意到事件发生的时间比13世纪《阿方索星表》预测的时间晚了1个月,比最近的《普鲁士星表》预测的时间晚了几天。
[8]
他后来说,这是他职业生涯的转折点。在莱比锡待了3年后,他回到哥本哈根。不久后,他的叔父去世,第谷从此自由地投身于天文学研究。
关于土星和木星会合的预测是不准确的,他意识到需要更精确的观测,于是他大幅改进了天文学家当时用于裸眼观测的仪器。在奥格斯堡工作时,他托人制作了一台四分仪,即一种用于测量90°以内角度的装置,半径约为19英尺
 。
。
1572年11月11日晚上,在回家吃晚饭的路上,他注意到仙后座中多了一颗星,而且比其他星都要亮,当时其位置几乎在他头顶正上方。为了测量这颗星与星座中其他恒星的角距,他使用了一个巨大的六分仪。这个装置由风干的胡桃木制成,带有青铜铰链,并通过精心设计的预防措施确保在每一组测量过程中都保持垂直和静止。在接下来的6个月里,随着这颗星的逐渐变暗,他对它展开了观察,发现它和星座中9个普通成员之间的角距没有明显变化。当时人们坚信(追随亚里士多德的观点)天空中只有月球以下的部分才会发生变化,但第谷计算出,如果这颗新星的位置没有月亮远,那么每年会有近1度的恒星视差(视差是指由于观察者位置的变化而导致的物体相对于背景的明显位移。物体离观察者越近,视差就越大),而且用他的仪器很容易就能测量出来。由此可见,在一个本应一成不变的天区发生了一些非常戏剧化的事情。他所看到的“ 新星 ”,就是我们现在所说的 超新星 。它们很少发生,在银河系中平均每个世纪不超过2次,而且是热核爆炸的结果,会释放出相当大的能量。
1572年超新星的一个副作用是第谷出名了。几年后,丹麦腓特烈二世赋予了他汶岛(这座岛的面积超过8平方千米,位于埃尔西诺以南)的终身使用权,还有王室在岛上所有租户和仆人的“租金和税款”、每年的慷慨资助,以及建造房屋和天文台的费用。
[9]
这些条件让人无法拒绝,之后第谷在那里建了一座天文台,根据现存的木刻画,库斯勒(Koestler)将其描述为“很像韦基奥宫(位于佛罗伦萨)和克里姆林宫的混合体”。在接下来的20年里,第谷一直住在这里,并作为一名天文学家完成了非常成功的工作,尽管他始终无法完全接受哥白尼体系——行星也许围绕太阳旋转,但地球必须是一切的中心。遗憾的是,第谷是一个傲慢且专横的地主,当克里斯蒂安四世接替腓特烈二世的王位后,双方的关系逐渐恶化,1597年,他不得不离开丹麦。16世纪末17世纪初,鲁道夫皇帝任命他为
帝国数学家
,年薪(至少在理论上)是3000弗罗林
 ,在离布拉格22英里
,在离布拉格22英里
 的贝纳特基还有一座城堡可以供其使用。他就是在那里遇到开普勒的。
的贝纳特基还有一座城堡可以供其使用。他就是在那里遇到开普勒的。

1600年开普勒和第谷的相遇对开普勒职业生涯的意义,堪比1563年土星和木星的会合对第谷事业的意义。28岁时,开普勒提出了解释行星轨道间距的非凡理论(一个并不完全成立的理论),并对天体运动的原因提出了新的问题和建议(这些问题和建议终将带来重大进展,但当时还没有)。他需要的也是他意识到自己需要的,是关于行星轨道更精确的数据,而第谷是最适合的人选。
2月初,开普勒在贝纳特基见到了第谷,尽管双方都明白对方的作用,但还有一些复杂的问题待解决:开普勒需要收入和住处,但第谷很难给予其承诺的薪水。另外,开普勒的助手和仪器也不在身边。在随后与第谷的艰难讨论中,开普勒的情绪在愤怒和深深的悔恨之间摇摆不定,不过双方和解之后,他安下心来继续工作。根据第谷的要求,开普勒从第谷的助手那里接过了关于火星的研究项目,后者没有取得多大进展。1个月后,开普勒回到格拉茨,主要是为了接他妻子。在那里,他继续研究确定火星轨道的问题,还发明了一个用于安全观测日食的装置,并在格拉茨中央广场上使用了这个装置。等他回到波希米亚时,第谷已经把他的研究中心从贝纳特基搬到了布拉格,以满足鲁道夫让 帝国数学家 离自己更近的愿望(估计是为了让他提供占星方面的建议)。在接下来的几个月里,开普勒继续研究火星,不过在1601年2月写给图宾根大学的老师的一封信里,他表达了自己的不满:
第谷在交流他的(天文)观测结果方面非常吝啬……我被允许每天使用它们。如果我能足够快地复制它们就好了!然而,我必须满足于从中做出选择……我可以接触到所有(观测数据),但首先我必须郑重地承诺对它们保密。 [10]
到了10月底,情况发生了巨大变化,第谷因急性尿潴留而死亡。葬礼后两天,皇帝任命29岁的开普勒为 帝国数学家 ,他担任这一职务直到生命最后一刻。开普勒对第谷去世的反应似乎和皇帝一样迅速。“我承认,”他在给英国的一个朋友的信中写道,“第谷去世后,我很快就利用了继承人不在或不谨慎的机会,把观测数据占为己有,或者可以说是篡夺了它们……” [11] 第谷的继承人自然很生气,几年里与其龃龉不止,但开普勒已经得到了他需要的东西。
有了第谷的数据所提供的详细而准确的信息,开普勒原本预计大约在一周内就能描述出火星的轨道。事实上,这花了他近5年的时间,虽然他完成时,揭示的不仅仅是轨道数据。延误的部分原因是两件事的干扰。 [12] 第一件事是他花了大量时间研究光学,并就这一课题写了一本450页厚的著作。 [13] 第二件事是1604年出现了一颗新星(另一颗超新星),它首次出现在土星和木星的会合点附近,离火星也不远。作为 帝国数学家 ,他受命解释这颗新星是如何产生的(一个天文学问题),以及它意味着什么(一个占星学问题)。他对这两个问题的处理方式截然不同:用大体上客观冷静的态度应对天文学问题,用大量的猜测应对占星学问题。由于这颗新星相对于其他固定星没有改变位置,他拒绝了它是由行星点燃的说法,并假定它是天上的物质聚集的结果,是由这些物质中固有的“建筑天性”造成的。当有人提出这种聚集可能只是原子偶然积累的结果时,他回应道:
对于这些争论者,我的对手,我要说一说我妻子而不是我的意见。昨天,当我写得很累,脑子因为考虑这些原子而昏昏沉沉时,妻子叫我吃晚饭,沙拉摆在我面前。“那么,”我大声说,“如果锡盘、生菜叶、盐粒、水滴、醋、油和鸡蛋片从古至今一直在空中飞来飞去,说不定最后会碰巧出现一份沙拉。”“是的,”我妻子说,“但不会像我做得这么美味,品相这么好。” [14]
尽管有这些干扰,但到1606年,开普勒还是成功地解决了火星轨道的问题。他开始使用托勒密和哥白尼用过的技术,但是经过大量研究,他得出结论,轨道不可能是圆形的,火星绕其轨道运行的速度也不可能是恒定的。但如果轨道不是圆形的,是什么形状呢?这是一个困难的问题,因为要回答它,他需要知道火星在其轨道上每一点的位置,但所有对火星的观测都是在地球上进行的,而地球本身也在运动。要想确定火星的实际运动,他首先需要知道地球是如何运动的。为了确定地球在任意时刻的位置,他需要效法导航员在船离海岸有一段距离但又不确定在哪里的做法:取两个固定点的方位,在地图上从这些点出发画线,这两条线的交叉点便是船的位置。问题是,这里只有一个明显的固定点——太阳(固定星派不上用场,因为它们太远了,其方位不会随着地球的运行而发生明显变化。不过,它们确实有助于确定整个太阳系在太空中的方位)。
面对这个问题,开普勒想出了一个如此优雅、如此反直觉的解决方案,以至于3个多世纪后,爱因斯坦称赞其为“真正的天才想法”。 [15] 开普勒把火星当作第二个固定点。尽管无法预测火星在某一时刻的确切位置,但他知道火星绕其轨道一周需要687.1个地球日。因此,每隔687.1个地球日(1个火星年),火星将处于相同位置。通过从第谷的大量数据中选出间隔正好为1个或多个火星年的观测数据,并只关注这些数据,他得出两个固定点,进而可以计算出地球在这些时刻的位置。在确定了地球轨道的精确形状和地球沿轨道运动的方式之后,他可以利用对火星的观测数据来确定火星的轨道和火星的运动方式。
通过这项工作和其他大量工作,开普勒认识到,3条相当简单的定律便足以描述行星的运动。
开普勒第一定律
涉及不对称的布局,因此他一开始对其心怀疑虑。该定律指出,每颗行星都在一个椭圆
 轨道上运动,太阳位于其中一个焦点(见图12)。不同行星的椭圆形轨道与正圆的差别程度不同。地球轨道接近正圆,火星轨道是所有行星中最不圆的——这就是为什么开普勒和他的前辈们在试图预测火星的运动时遇到了那么大的困难,因为他们假设火星运行在圆形轨道上。
轨道上运动,太阳位于其中一个焦点(见图12)。不同行星的椭圆形轨道与正圆的差别程度不同。地球轨道接近正圆,火星轨道是所有行星中最不圆的——这就是为什么开普勒和他的前辈们在试图预测火星的运动时遇到了那么大的困难,因为他们假设火星运行在圆形轨道上。
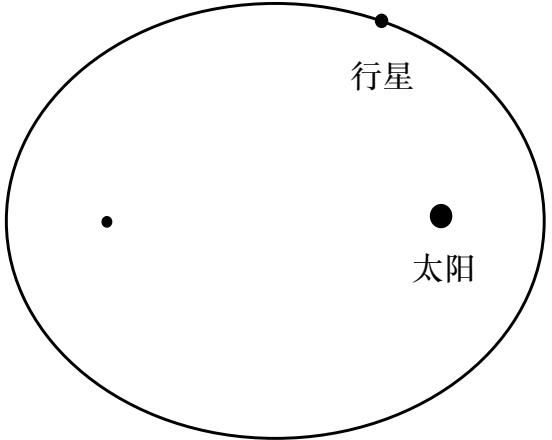
图12 椭圆形轨道,太阳位于其中一个焦点
开普勒第二条定律 是,行星绕其轨道运行的速度不是恒定的,而是接近太阳时加速,远离太阳时减速。更准确地说,在一颗行星沿其轨道运动的过程中,行星和太阳之间的连线在相同的时间内扫出的面积相等(见图13)。
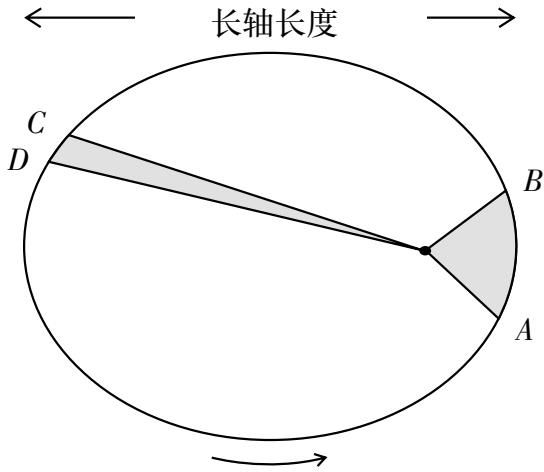
图13 开普勒第二定律示意图
开普勒第三条定律 (直到1618年,他46岁时才发现)是,如果你比较不同的行星,你会发现每颗行星完成一次公转所需时间的平方与椭圆长轴的立方成正比(见图13)。从年轻时起,开普勒就想知道行星与太阳的距离和它绕太阳运行一周所需的时间之间有什么关系。现在他有答案了。

利用第谷的数据,开普勒不仅成功地发现了行星如何运行,还能够用3个简单的数学公式来描述它们的运动。这确实优雅且简洁。下一步,也就是了解为什么行星会以这种方式运动?就只能等待牛顿出现了,不过开普勒确实提出了一些建议。这些建议虽然不正确,却令人耳目一新,因为它们基于已知的物理学,而不是对柏拉图多面体的幻想(如他早期的工作),也不是基于毕达哥拉斯学派证明与音乐和谐相关的数学模式以及可能与“宇宙和谐”相关的数学模式之间的类比(如他后期的工作)。早期,他认为太阳可能提供了使行星旋转的力量,但为了解释行星的旋转,他认为太阳在某种程度上就像一把扫帚。事实上,他曾经好奇太阳本身是否在绕着自己的轴旋转。几年后,伽利略对太阳黑子的观察表明,事实的确如此。
他意识到物体之间存在引力。他不仅提出月球的引力是潮汐发生的原因,还在《新天文学》( Astronomia Nova ) [16] 一书——出版于他38岁时,包含他的前两个行星运动定律——的序言中写道:
引力是同类
 物体之间相互统一或者接触的倾向……因此,地球对石头的吸引力要远远大于石头对地球的吸引力……
物体之间相互统一或者接触的倾向……因此,地球对石头的吸引力要远远大于石头对地球的吸引力……
如果把两块石头放在彼此靠近的一个空间的任意位置,并且在第三个同类物体的力的范围之外,那么它们就会以类似磁体的方式会合于一个中间点,每一块石头都按其质量的比例接近另一块石头。 [17]
他的困难在于,在没有 动量 和 惯性 这类现代概念的情况下——尽管他后来引入了含义较为狭隘的“惯性”一词,他无法理解仅靠引力(或者就他当时的理解而言,即太阳的磁力)是如何让行星绕太阳旋转的[9年后,威廉·吉尔伯特(William Gilbert)证明了地球本身就像一个巨大的磁铁]。
尽管人们终将认识到开普勒前两条定律的重要性,但它们在当时没有引起什么波澜。在接下来的两年里,开普勒将注意力转向了改进望远镜——荷兰的眼镜制造商在1608年发明的望远镜,使伽利略得以发现木星的卫星。1611年,开普勒的妻子死于“匈牙利热”(可能是斑疹伤寒),他6岁的儿子也于同年死于天花。第二年,他不得不逃离布拉格,因为路德教派在布拉格已经不被接受了。接下来的14年,他是在林茨度过的:再次结婚并生育了好几个孩子;撰写了一部关于哥白尼天文学的长篇论著;在他母亲遭受漫长的女巫审判期间为她辩护;(重新使用他更神秘的模式)写下了《世界的和谐》一书,该书的最后一章包含他完全不神秘的第三定律。1626年,由于深陷三十年战争,开普勒第三次出于宗教方面的原因搬家。
 他搬到了符腾堡州的乌尔姆市。在那里,也就是第谷去世26年后,开普勒终于出版了人们期待已久且备受赞誉的《鲁道夫星表》——第谷曾答应皇帝要为其制作出第一份现代天文表,而开普勒也曾向垂死的第谷保证,他将完成这一使命。
他搬到了符腾堡州的乌尔姆市。在那里,也就是第谷去世26年后,开普勒终于出版了人们期待已久且备受赞誉的《鲁道夫星表》——第谷曾答应皇帝要为其制作出第一份现代天文表,而开普勒也曾向垂死的第谷保证,他将完成这一使命。
在结束对开普勒的介绍之前,我还要提及另一件事。尽管在关于哥白尼天文学的著作中,开普勒没有论及现代惯性概念——除非受力不平衡,一个物体会保持其当前速度的趋势——但他确实在更有限的意义上引入了“惯性”
 这个词。他用它来衡量一个静止的物体保持静止的趋势。这个词在现代的狭义用法是,如果你把一个乒乓球和一个台球放在光滑的水平面上,然后用力拍打这两个球,乒乓球会“动若脱兔”,台球则缓慢移动,因为它的惯性更大。只有等到伽利略(尽管他实际上没有使用“惯性”一词)将
其含义扩展到对一个物体保持其当前运动速度和方向的倾向的衡量
时,这个概念才开始极大地促进我们对运动(包括行星运动)的理解。
这个词。他用它来衡量一个静止的物体保持静止的趋势。这个词在现代的狭义用法是,如果你把一个乒乓球和一个台球放在光滑的水平面上,然后用力拍打这两个球,乒乓球会“动若脱兔”,台球则缓慢移动,因为它的惯性更大。只有等到伽利略(尽管他实际上没有使用“惯性”一词)将
其含义扩展到对一个物体保持其当前运动速度和方向的倾向的衡量
时,这个概念才开始极大地促进我们对运动(包括行星运动)的理解。
伽利略的贡献到下一章再讲。在本章尾声,我希望思考一下,是什么让开普勒对两颗彼此接近但在空间中孤立的石头之间相互吸引的效果做出了如上文所述的论断。那句相当接近于万有引力定律的话指出,两块石头:
……会合于一个中间点,按其质量的比例接近另一块石头。
我们现在知道,这种行为将遵循牛顿的第二和第三运动定律,但开普勒在牛顿出生前30多年就写下了这句话。可以想象,出于某种原因,他当时(正确地)认为,在不受其他影响的情况下,这些石头会以这样一种方式运动,即隔绝系统的质量中心
 不会改变。但这也显示出一种非凡的洞察力,如果他的论断基于这个想法,我们倒是期望他提到了这一点。我的同事皮耶罗·米廖拉托(Piero Migliorato)向我提出的一个更有可能的假设是,他正试图对落石情境中的不对称性做出解释。两块相互接近但在空间上孤立的石头会移向对方。但当一块石头落向地球时,地球并没有表现出向着石头上升的可察觉趋势。将这种不对称性与石头、地球质量之间巨大的不对称性联系起来似乎很自然。毫无疑问,开普勒的确相信地球会向石头方向轻微上升。他在1605年写给下萨克森州的一个同事的信中写道:
不会改变。但这也显示出一种非凡的洞察力,如果他的论断基于这个想法,我们倒是期望他提到了这一点。我的同事皮耶罗·米廖拉托(Piero Migliorato)向我提出的一个更有可能的假设是,他正试图对落石情境中的不对称性做出解释。两块相互接近但在空间上孤立的石头会移向对方。但当一块石头落向地球时,地球并没有表现出向着石头上升的可察觉趋势。将这种不对称性与石头、地球质量之间巨大的不对称性联系起来似乎很自然。毫无疑问,开普勒的确相信地球会向石头方向轻微上升。他在1605年写给下萨克森州的一个同事的信中写道:
……不光是石头接近地球,地球也会接近石头,它们对间隔空间的划分与它们的重量成反比。 [18]
如果一个物体的惯性(开普勒所说的狭义的惯性)与它的质量成正比,那么落石和地球的惯性差异就为落石情境的不对称性提供了简单的解释。同样,如果惯性与质量成正比,那么两块相互接近并在空间中隔离的石头就会相向移动,它们各自移动的距离与对方的质量成正比。尽管开普勒直到1618年才写下关于惯性的文章,但看来他早在十多年前就在思考这个问题了。


