第3章
把天堂带入凡尘
正是伽利略在研究地面物体运动方面新颖而优雅的方法,最终使人们得以将地面物体运动和天体运动联系起来。
1564年,伽利略·伽利雷生于比萨一个佛罗伦萨贵族家庭的破落支系。
[1]
他的父亲文森佐(Vincenzo)是作曲家、优秀的鲁特琴演奏家和音乐理论方面的作家。作为音乐理论家,他发现纯五度音程不仅可以由两根长度比为3:2且处于相同张力下的弦产生,也可以由两根长度相同但承受的拉力比为4:9(反比的平方)的弦产生。他的儿子似乎继承了他将数学分析和直接实验相结合的兴趣。文森佐本来希望儿子能成为商人,重组家族财富,但伽利略显而易见的才智使上大学成了一条有吸引力的人生之路。由于他的父亲知道学数学和音乐的经济回报很低,所以让他在比萨学习医学。第一年,到比萨大教堂做礼拜时,伽利略的思绪却在神游
 ,他注意到,一盏被设置为摆动状态的油灯在幅度越来越小的情况下保持相同的频率。后来他对钟摆进行研究,并证明了钟摆的频率与摆锤的重量无关。这时的他对数学还知之甚少,但一次偶然的机会,他听了他父亲朋友的一场几何学讲座,深受启发。由于资金短缺和未能获得学医的奖学金,他在21岁时没拿到学位就离开了比萨。他回到家人当时居住的佛罗伦萨,开始自学数学。4年后,他被拒绝向他提供奖学金的大学任命为数学讲师。回到比萨后,他开始研究物体运动,尤其是地面物体运动,并随着研究工作的推进推翻了当时仍然盛行的亚里士多德的物理学,而这则是他对科学做出的最重要贡献。
,他注意到,一盏被设置为摆动状态的油灯在幅度越来越小的情况下保持相同的频率。后来他对钟摆进行研究,并证明了钟摆的频率与摆锤的重量无关。这时的他对数学还知之甚少,但一次偶然的机会,他听了他父亲朋友的一场几何学讲座,深受启发。由于资金短缺和未能获得学医的奖学金,他在21岁时没拿到学位就离开了比萨。他回到家人当时居住的佛罗伦萨,开始自学数学。4年后,他被拒绝向他提供奖学金的大学任命为数学讲师。回到比萨后,他开始研究物体运动,尤其是地面物体运动,并随着研究工作的推进推翻了当时仍然盛行的亚里士多德的物理学,而这则是他对科学做出的最重要贡献。
亚里士多德区分了“自然运动”和“受迫运动”,前者如重物落地或者空气升腾,后者如飞矢离弦或者马拉战车。他认为,所有运动,无论是自然的还是受迫的,都是由“动力”引起的,而且只要运动在持续,就可以肯定力在发挥作用。动力越大,运动就会越快。两匹马拉战车的速度比一匹马的快,而且他认为(并不总是正确的)较重物体下落的速度比较轻物体的快。事实上,他还进一步(错误地)宣布,物体的下落速度与它的重量成正比。
他意识到一个困难:如果运动只在力起作用的时候持续,那么为什么箭离开弓后还能继续飞?他不得不假设周围的介质起了作用,弓弦在推动箭的同时也推动了介质,而且在一段时间内,介质必须取代弓弦的作用。他认为,所涉及的介质不可能是空气,因为空气不可能使一个重物充分移动,肯定有某种更神秘的介质参与。
到伽利略的时代,亚里士多德的这些观念已经存在了近2000年,其中一些似乎已经成为常识。但物体下落的速度与其重量成正比的说法很容易被一个简单的“真实实验”证伪,还可以被一个优雅的“思想实验”证明会导致矛盾的结论。这两者都是伽利略所为。
在真实实验中,伽利略从很高的地方同时扔下一个重达100多磅
 的炮弹和一个半磅重的火枪弹,它们几乎同时着地。长期以来,人们一直认为这个实验是在比萨斜塔上做的——也许是作为一场引人注目的公开演示,而考虑到伽利略开始这方面研究时正身处比萨,所以这种猜测貌似是可信的,尽管有人认为这个故事被“润色”过。
的炮弹和一个半磅重的火枪弹,它们几乎同时着地。长期以来,人们一直认为这个实验是在比萨斜塔上做的——也许是作为一场引人注目的公开演示,而考虑到伽利略开始这方面研究时正身处比萨,所以这种猜测貌似是可信的,尽管有人认为这个故事被“润色”过。
思想实验虽然没有那么引人注目,但它所展现的朴素性、独创性、简洁性、意外性和说服力非常优雅。 [2] 假设两个重量相差很大的物体被一根绳子绑在一起,然后从高处落下。如果亚里士多德是正确的,那么重的物体会下落得更快,并趋于增加轻的物体的速度,而轻的物体会下落得更慢,并趋于拖慢重的物体的速度。因此,这对被绑在一起的物体下落的速度应该介于它们分开下落的速度之间。但如果亚里士多德是正确的,你也可以说,这对组合的重量始终大于其中任意一个,因此,组合下落的速度应该比它们单独下落的速度快。导致矛盾结论的一组假设一定有问题。
很容易理解亚里士多德为什么会认为重物比轻物下落得快——一枚硬币要比一根羽毛下落得更快,但他关于重量和下落速度成比例的观点能够流传近2000年,这很不寻常。不是每个人身边都有一座斜塔,但将2枚重量不同的硬币同时扔下并观察到它们同时落地就很容易。
虽然伽利略的论点令人信服,但无论是这些论点还是他讽刺的态度都没能让他获得哲学系传统亚里士多德派的青睐。当他因批评一项疏浚来航(Leghorn,里窝那的旧称)港的计划而激怒了美第奇家族,又因写了一首关于学术着装的戏谑诗而激怒了大学的教务人员时,他开始发现自己在大学的工作既不舒适也不安全。在3年合同期满后,他离开了比萨,并在他的朋友、赞助人和数学家吉多巴尔多·德尔·蒙特(Guidobaldo del Monte)侯爵的帮助下,在帕多瓦大学担任数学教授。当时他28岁,之后在帕多瓦度过了18年成绩斐然的时光。
帕多瓦是威尼斯共和国的一部分,它的大学已有近400年的历史,相对来说不太受罗马天主教会的控制,因此吸引了欧洲各地的学生(伽利略在那里时,威廉·哈维曾到访过)。伽利略安顿下来,教授几何、力学、军事工程和天文学,并继续他在运动方面的研究。在推翻了亚里士多德关于自由落体的观点之后,他不得不面对这样一个问题:自由落体下落的速度有多快,以及它们的速度在下落过程中是如何变化的?解决这个问题的困难在于,自由落体的速度太快了,没有有效的方法来追踪这一运动。
因此,他没有研究自由落体,而是研究了光滑沉重的青铜球从倾斜的抛光木板上滚落时的加速度方式。通过使坡度平缓(有时略低于2°),他可以让球的速度慢到可以测量。他最成功的测量方法之一是利用了人类对任何偏离规律节奏的敏感度。如果你听的是间隔半秒的有规律节拍,当一个节拍提早或延迟了哪怕三十二分之一秒时,几乎每个人都能发现这一错误。伽利略(也是一名鲁特琴演奏家)所做的是在木制的斜坡上每隔一段距离系一圈肠线,就像鲁特琴琴颈上的弦品一样。为了确定线圈的初始位置,他随着节奏强烈的曲子的节拍释放球,并在随后的每个节拍上大致标记出球的位置。然后他把线圈套好,使每个标记点上都有一条线穿过球的路径。球走过线圈的声音是可以被听到的,于是在随后的运动中,他可以调整线圈的位置,直到球走过线圈的声音与音乐的节拍完全一致。这样相邻的线圈之间的距离就可以告诉他球在连续的等长时段内所走的距离。 [3]
他的发现使他大吃一惊。如果在第一个区间内移动的距离被定义为1个单位,那么在第二个区间内移动的距离就变成了3个单位,第三个区间是5个单位,第四个区间是7个单位,依此类推,这是一个“奇数定律”。将球走的总距离和总用时比较之后,他发现距离与时间的平方成正比。如果球从斜坡滚下的行为是物体自由下落的向导,那么他最终得到的是“自由落体定律”。但这意味着什么呢?直到几年后,他才意识到,奇数定律以及所走距离与所用时间的平方成正比的关系仅仅是这样一个事实的结果:当球从斜坡上滚下时,其速度随着时间线性增加。换句话说,加速度是恒定的。
这些实验优雅且重要,但伽利略用球和斜面做的另一组实验也不容小视,后者使他得出了惯性的概念——虽然他没有使用“惯性”一词。在用一对相向而设的斜面所做的实验中,他发现球从一个斜面滚下来,然后从对面的斜面滚上去,几乎达到了它开始滚落时的高度。即使坡度不同,也是如此(见图14)。摩擦力越小,球滚上去就越接近它的起始高度。如果第二个平面的坡度比第一个平面小,那么球就必须沿着第二个平面走更远才能接近原来的高度。如果第二个平面的坡度被不断放缓,球就会走得越来越远。事实上,伽利略的结论是,如果第二个平面是水平的,以及如果摩擦力可以被消除,那么球将以恒定的速度沿着平面一直滚动。这不仅与“只要运动持续,就肯定有力在起作用”的观点相矛盾,还接近于预见到牛顿的第一运动定律——有时被称为“惯性定律”, 即除非受到力的作用,否则物体将保持静止或者匀速直线运动 。
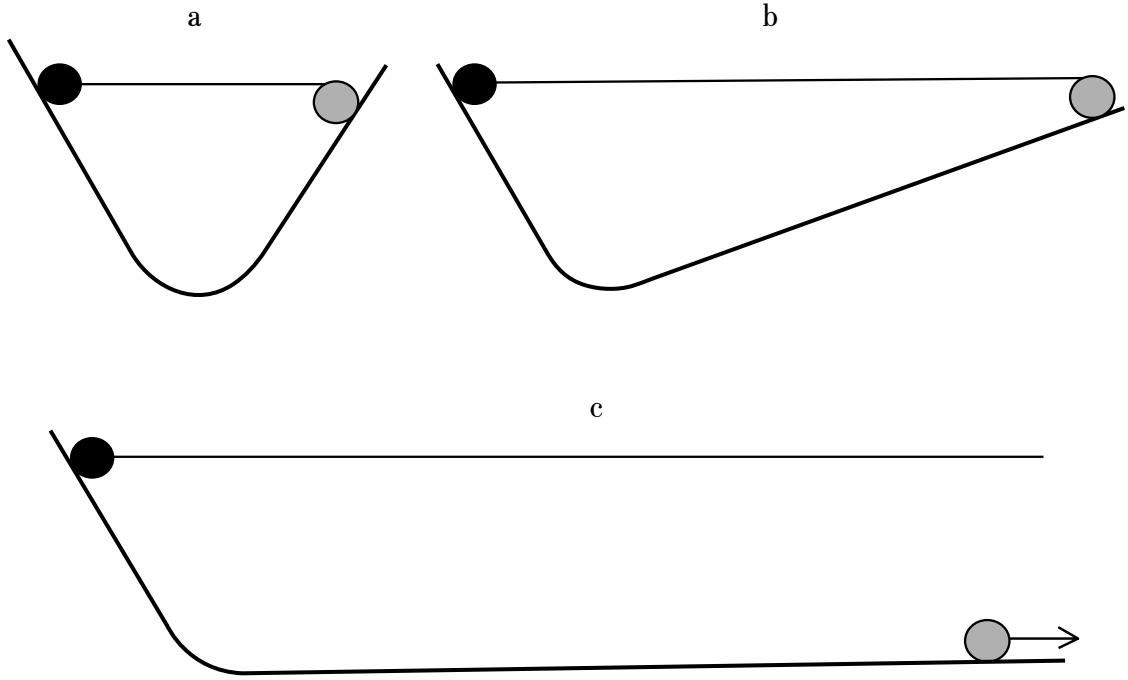
图14 伽利略的实验;用球在几乎没有摩擦力的光滑平面上滚动,这使他得出了惯性的概念
在确立了“自由落体定律”和“惯性”的概念后,伽利略稍做修改,将这些关于球和斜面的实验更进一步,得到了两个更重要的结论。和前面的实验一样,他让球从斜面跑到水平面上,但这一次的水平面是桌面,当球离开桌子边缘时,它会沿着弯曲的路径落到地面上。通过改变球在斜面上开始滚落的高度,他可以改变球沿桌面滚动的速度。有趣的问题是:桌子上的水平速度是如何影响球落地的路径的?对于任意一个速度,球到达地面的路径是什么形状?
他所期望的是,当到达桌子边缘时,球的稳定水平运动将继续保持不变,但球也会同时进行获得具备自由落体条件的竖直向下运动,也就是说下降的距离与时间的平方成比例。如果球以桌边为起始的水平位移与它离开桌边的时间成正比,而竖直位移与时间的平方成正比,那么球到地面的路径必定是半条抛物线, [4] 而这正是他所发现的(见图15)。这在两个方面都很重要:首先,它表明一个物体在两个相互垂直的方向上的运动可以彼此独立改变。其次,它提出了对当时而言的新观点,即抛掷物的飞行路径是抛物线,是由不同力引起的运动的共同结果。通过如此简单的实验得出如此多的重要结论,这不仅是非常优雅的科学,更是一种新颖科学——对真实的运动进行数学层面的描述,而不是试图将其纳入先入为主的完美圆圈或者其他概念。
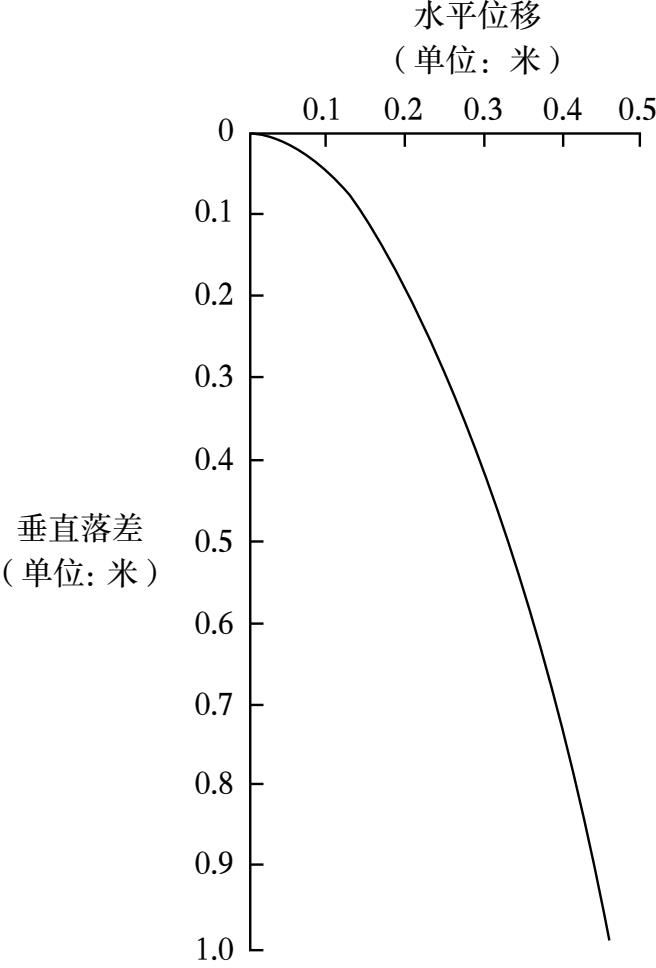
图15 伽利略展现抛物线运动的实验

尽管我所讨论的大部分研究伽利略1609年前就在帕多瓦完成了,但他直到生命接近尾声时才将它们发表(顺带一提,这就是开普勒在1620年前后还可以发表一篇关于惯性不太成熟的论述的原因)。拖延的主要原因是,和开普勒一样,研究动力学时,伽利略被荷兰眼镜制造商发明望远镜的报道分散了注意力。1609年访问威尼斯时,他听说那些报道都是真的,而且当时还有一个外国人将望远镜带到了意大利帕多瓦。但当他回到帕多瓦时,那个外国人已经离开了,因此已经了解荷兰这一发明基本设计的伽利略决定自己制作一个。他不仅成功了,还使望远镜达到了30倍的放大率,这是使用凸透镜和凹目镜的荷兰系统所能达到的最高水平。 [1] 他在1610年1月初开始使用望远镜,3月底,他发表了《星际信使》。这是一本48页的8开本薄册子,描述了月球上的山脉和陨石坑,揭示了银河系是由无数星星组成的,描述了许多新发现的固定星,以及(最值得注意的)关于木星有4颗卫星的报告。在哥白尼日心说体系中,地球和它的卫星月球不再显得格格不入。
早期对这一体系的反对意见是,如果地球每天都在旋转,那么地球表面的人(除非他们生活在北极或南极附近)会移动得非常快——生活在赤道附近的人移动的速度约为1000英里/时,而生活在帕多瓦的人的移动速度则接近前者的四分之三。但如果地球表面以这样的速度移动,你可能会认为,任何不附着在它上面的东西(比如从树上掉下来的苹果,或者被扔到空中的石头)都会迅速被抛在后面。
在伽利略之前,应对这种反对意见的标准方法是参照英国天文学家托马斯·迪吉斯(Thomas Digges)提出的那种思想实验。他在1576年指出,如果一块石头从快速行驶的船只的桅杆上落下,它会落在桅杆底部,而不是更靠后的位置。1600年被烧死在火刑柱上的意大利人乔尔丹诺·布鲁诺(Giordano Bruno)——他还是多米尼克派修士、哥白尼派天文学家和记忆方面的专家——描述过这个思想实验的一个更精细、更优雅的变体。在布鲁诺思想实验的一个版本中,我们需要想象一艘有高大桅杆的船在运河上快速行驶,并且运河上有一座高度刚好能让船上桅杆通过的桥。如果一个人在船从桥下通过时从桅杆顶部扔下一块石头,同时另一个人从桥上扔下一块石头,那么从桅杆处扔出的石头将落在甲板上紧挨着桅杆的位置,而从桥上扔下的石头将落在更后面的位置。换句话说,随着船向前移动的石头在下落过程中继续向前移动,而没有随着船向前移动的石头在下落过程中则不向前移动。以此类推,在快速旋转的地球上,从树上掉下来的苹果在下落过程中会继续朝同一方向运动,并且(如果不受干扰)最终会准确地落在它起始所在树枝的正下方。
伽利略证明惯性的实验为这些思想实验中所描述的行为提供了直接解释,从而为驳回对哥白尼理论的传统异议提供了坚实的基础。然而,可能因为害怕被嘲笑,伽利略继续教授托勒密体系。甚至他的《星际信使》一书中也没有明确推荐哥白尼的观点。在如此缄默的情况下,这本书几乎一夜成名,并立即引起了争议。尽管威尼斯元老院提出给伽利略的薪水翻倍,但他还是辞去了帕多瓦大学的教授一职,然后成为托斯卡纳大公国的宫廷首席数学家和哲学家,以及比萨大学没有教学任务的首席数学家的职位(该职位在400年后听起来仍然颇有吸引力)。1610年,伽利略用他的望远镜看到了金星的相位,并意识到这在哥白尼体系中很容易解释,但在托勒密体系中完全无解。1613年,在一本关于太阳黑子的书中,他第一次谈到现在被称为“转动惯量”的概念——在没有摩擦力或其他力的情况下,刚体 绕着穿过其质心的轴转动 而保持无限旋转的能力,并为哥白尼体系提出了强有力的论据(第一次在出版物中提及)。奇怪的是,他一生中从未对开普勒的椭圆轨道或行星定律表现出任何兴趣。他似乎对圆形轨道情有独钟。
伽利略突然对哥白尼产生兴趣似乎源自一个有意识的决定,因为他在给大公秘书的信中写道:“我的一生和以后的生活从此都将取决于哥白尼学说的建立。” [5] 事实证明,千真万确。次年年底,他受到神职人员谴责,他晚年的悲剧也随之开始。1616年,教会宣布哥白尼的观点为异端,但在1624年,伽利略获准用公正客观的方式为“日心说”和“地心说”辩护。在接下来的6年里,他创作了《关于托勒密和哥白尼两大世界体系的对话》一书。这本书用意大利语写成,采用的是对话形式。其中一个代表作者,一个是聪明的聆听者,第三个人是好心的辛普利邱(Simplicio)。这本书公然无视伽利略获得许可的相关条件。1633年,伽利略因异端邪说受审,被判处终身监禁,后来改判为软禁。在位于佛罗伦萨城南阿切特里的别墅里,他写出了《关于两门新科学的论述和数学发现》( Discourses and Mathematical Discoveries Concerning Two New Sciences )。这是他写的最后(也是最重要的)一本书,书中最后一节中包含了他关于运动的关键性研究,其中大部分是20多年前完成的。禁书审定院禁止印刷他的任何书籍,所以手稿不得不被偷运出国,并于1638年在莱顿出版。
伽利略于1642年1月去世,而次年,牛顿出生。

到1642年,距离哥白尼的《天体运行论》发表已经过去了近一个世纪,牛顿出生时的知识界与哥白尼曾经与之斗争的那个世界已经截然不同。开普勒的行星运动三大定律为行星的行为方式提供了令人满意的解释,而伽利略的自由落体定律和抛体运动规律(及惯性的概念)不仅推翻了反对地球运动这一观点,还将亚里士多德从神坛推下,并帮助物理学成为一门实验科学。牛顿将对这5个定律做出非常优雅的解释,他展示了它们是如何依赖于3个非常简单的运动定律和一个非常简单的重力吸引定律的。不过在那之前,他要先熬过一个像开普勒那样充满忧愁的童年。 [6]
他36岁的父亲拥有伍尔斯特霍普庄园(林肯郡一座简朴的石头农舍),是一位成功的(尽管目不识丁)自耕农,但在牛顿出生前3个月意外去世。牛顿是个早产儿,后来有人告诉他,他出生时:
个头太小了,小到几乎可以把他放进一夸脱的壶里,还很虚弱,他们不得不用一条垫枕围住他的脖子,才能帮助它立在肩膀上。他活下来的可能性太小了,当两个女人被派到北威瑟姆,为他找一些救命的东西的时候,两人竟坐在路边的一节梯磴上,说不必着急,因为她们确信孩子等不到她们回来就会死。 [7]
他3岁时,他的母亲嫁给了年老的鳏夫邻居(北威瑟姆的一个牧师),并搬到他的教区,把年幼的牛顿留在了伍尔斯特霍普,由他的外公外婆照顾——他从来没有对他们表示过什么好感。小时候,他在当地的两所“家庭幼儿学校”上学。11岁时,他的继父去世,他的母亲带着第二次婚姻的3个孩子回到了伍尔斯特霍普。1年后,他成为格兰瑟姆——玛格丽特·撒切尔(Margaret Thatcher)就出生在这里——历史悠久的国王学校的学生。在那里,他和当地一个药剂师及其3个继子女住在一起。牛顿与女孩相处得更好——他为她们的玩偶制作家具,但与药剂师家及学校里的男孩相处得并不愉快。他喜欢画画,动物、船、植物、查理一世和学校校长都是他的绘画对象,也喜欢制作机械玩具,比如以老鼠为动力的磨坊、火红的风筝、钟表,以及可以坐在里面转动曲柄驱动的四轮车。他还痴迷于日晷。他的成绩时好时坏,经常落后,然后再迎头赶上。除了《圣经》里的知识,他还学习了大量的拉丁文和少量的希腊文,可能还有少量数学知识。 [8]
他快17岁时,他的母亲把他从格兰瑟姆接回来帮助管理农场——他对这项工作既没有兴趣也没有天赋,更愿意把时间花在制造小玩意儿上,而不是照看羊群上。另外,访问格兰瑟姆时,他更愿意在药剂师家里看书,而不是尝试出售农产品。幸运的是,他的舅舅——生活在距离伍尔斯特霍普约2英里的伯顿科格尔斯(Burton Coggles)的牧师——以及独具慧眼的校长一起说服他母亲相信,务农并不适合他。他被允许回到学校为上大学做准备。
1661年6月,牛顿以勤工俭学者
 的身份被剑桥大学三一学院录取,也就是他舅舅曾就读的学校。在头两年里,他学习了以亚里士多德哲学为主的传统课程,但在第三年和第四年,他开始涉猎其他学科,阅读笛卡儿的《几何学》和《哲学原理》、开普勒的《折射光学》、伽利略的《关于托勒密和哥白尼两大世界体系的对话》和《星际信使》,以及伽桑狄对哥白尼天文学的阐述。他还开始研究数学问题。1665年夏天,大学因瘟疫而关闭,牛顿在那一年和次年的大部分时间都是在林肯郡度过的,不过他经常回剑桥大学的图书馆。
[9]
在那两年间,他的智力活动惊人,为他日后在数学(包括他的“流数法”,也就是微积分的基础)、光学(包括发现白光可以分成大约7种颜色)和力学(包括天体力学)方面的工作奠定了基础。当然,与本章相关且值得详细探讨的是他在力学方面的研究。
的身份被剑桥大学三一学院录取,也就是他舅舅曾就读的学校。在头两年里,他学习了以亚里士多德哲学为主的传统课程,但在第三年和第四年,他开始涉猎其他学科,阅读笛卡儿的《几何学》和《哲学原理》、开普勒的《折射光学》、伽利略的《关于托勒密和哥白尼两大世界体系的对话》和《星际信使》,以及伽桑狄对哥白尼天文学的阐述。他还开始研究数学问题。1665年夏天,大学因瘟疫而关闭,牛顿在那一年和次年的大部分时间都是在林肯郡度过的,不过他经常回剑桥大学的图书馆。
[9]
在那两年间,他的智力活动惊人,为他日后在数学(包括他的“流数法”,也就是微积分的基础)、光学(包括发现白光可以分成大约7种颜色)和力学(包括天体力学)方面的工作奠定了基础。当然,与本章相关且值得详细探讨的是他在力学方面的研究。
1665年,哥白尼体系和托勒密体系之间的斗争早已结束。不过,仍然有一个问题悬而未决:开普勒的研究描述了行星是如何运动的,但这并没有解释它们为什么会这样运动。把太阳的光线——或来自太阳的其他某种“辐条”,看作扫帚是一种很吸引人的想法,但这似乎不太可能,而且与开普勒的第三定律也不太容易调和。虽然伽利略的工作对地面物体力学给出了令人满意的解释,但将他的研究应用于天体问题并不简单。由于惯性倾向于保持直线运动,笛卡儿通过假设行星被一片无所不在的以太中的涡流驱动,来解释行星绕其轨道的运动。对于行星轨道问题,另一个令人困惑和不满意的解决方案是“圆周惯性”这个被误导的概念。在伽利略的实验中,球沿着平坦、无摩擦的表面持续匀速运动,如果人们不把这个无摩擦的表面看作一个完美平面,而是看作一个平行于地球圆周的光滑表面,那么直觉上似乎可以认为这个球会继续沿着圆周滚动,而且如果不受干扰,它将永远滚动下去。这个论点是合理的,但解释的不是“圆周惯性”,而是直线惯性和地球引力的组合——正是这种组合使卫星保持在其轨道上。
1665年前后,为了寻求对行星运动的解释,牛顿开始对约束物体绕圆周匀速运动所必需的力产生了兴趣。根据他关于惯性和后来被称为他第二运动定律的知识,他能够证明这个力必须指向圆心,而且其大小必须与速度的平方成正比,与半径成反比。但通过对比各大行星的轨道周期和它们与太阳的距离而得到的开普勒第三定律表明,这些行星与太阳的平均距离和轨道周期(以及由此而得的速率)不是独立的变量。该定律是,轨道周期的平方与行星和太阳之间的平均距离的立方成正比。对于接近圆形的轨道,行星的速率几乎是恒定的,而轨道周期与该速率成反比。把这些陈述放在一起,写上几行代数式, [10] 牛顿得出了一个惊人结论。如果太阳对某一特定行星施加的引力与太阳中心至行星中心的距离的平方成反比,那么引力便足以解释不同行星绕其轨道的运动。这个结论是在假设行星的轨道接近圆形的情况下得出的,大约16年后,他证明了同样的结论适用于更扁的椭圆形轨道。
许多年后,年迈的牛顿在肯辛顿花园里的苹果树下喝茶时,他告诉老朋友斯图克利博士:
他当时的处境和从前一样,引力的概念出现在他的脑海中。这是他坐在那里沉思的时候,一个苹果掉了下来而引起的。 [11]
牛顿侄女的丈夫、牛顿担任造币厂厂长时的助手约翰·康迪特(John Conduitt)对此有更全面的描述:
1666年,他再次从剑桥大学退休……回到生活在林肯郡的母亲身边,当他在花园里(可能是在伍尔斯特霍普庄园)思考时,他想到引力的作用(将苹果从树上带到地上)未必局限于离地球一定距离之内,而是一定比通常认为的要远得多。他想,为什么不会一直延续到月球呢?倘若果真如此,那一定会影响它的运动,也许正是引力将它保持在轨道上。于是他开始计算这个假设会产生怎样的影响…… [12]
这些故事很吸引人,但很难相信是一个苹果的掉落让牛顿第一次想到地球的引力可能延伸到月球。开普勒很久以前就提出了月球在引起潮汐方面的作用,如果月球的引力可以延伸到地球,那么假设地球的引力没有延伸到月球就很奇怪了。不过很有可能是,苹果的掉落提醒了牛顿地球引力在维持月球轨道方面可能发挥的作用,然后他意识到他发现的万有引力平方反比定律可以验证这一假设。
由于月球与地球中心距离大约是苹果与地球中心距离的60倍,
[13]
所以他认为地球引力在月球上的强度应该是它在地球表面强度的1/3600。那么,关键问题是,这种引力强度能使月球保持在绕地球的轨道上吗?
 答案似乎是低了大约11%——可能是因为他使用的地球半径值不准确。虽然过了一段时间,当被问及这个强度是否正确时,他回答说“差不多”,但他显然对这个结果不满意,因为他已经放弃这个课题长达20年之久,并一度认为月球除了对引力有反应外,还可能被一个以太旋涡裹挟着,正如笛卡儿所提议的那样。
答案似乎是低了大约11%——可能是因为他使用的地球半径值不准确。虽然过了一段时间,当被问及这个强度是否正确时,他回答说“差不多”,但他显然对这个结果不满意,因为他已经放弃这个课题长达20年之久,并一度认为月球除了对引力有反应外,还可能被一个以太旋涡裹挟着,正如笛卡儿所提议的那样。
尽管牛顿在17世纪60年代就开始思考他的“运动定律”,但直到1685年,他40多岁时写出《原理》,才确定这些定律的最终形式。在对惯性原理犹豫了20年之后,他最终采用了伽利略和笛卡儿讨论过的直线惯性的概念。他的 第一定律 (通常被称为“惯性定律”),用现代语言表达是这样的:
一切物体在没有受到力的作用时,总保持静止状态或匀速直线运动状态。
他的 第二定律 也是基于他20年前就开始探索的想法。它是:
物体的加速度跟物体所受合力成正比,与物体的质量成反比。
这里的加速度是指速度的变化,而速度是指给定方向上的速率。因此,速度的变化可以是速率的变化,也可以是方向的变化,或者两者都有。月球绕着它近乎圆形的轨道以稳定的速度运行,但它在不断改变相对地球的方向。它有一个朝向地球的稳定的加速度,与地球对它的稳定引力相应。火星在一个更扁的椭圆轨道上,太阳在椭圆的一个焦点上,随着作用在它身上的引力的变化,它的速率和运动方向也都在变化。
牛顿第二定律很好地解释了伽利略的自由落体定律。因为下落物体的质量没有变化,而且它所受的重力作用也变化不大,所以加速度是恒定的。
牛顿 第三定律 也起源于1666年完成的工作,当时牛顿对两个物体碰撞时会发生什么很感兴趣。它的陈述通常简洁却有失明晰:
每一个作用都有一个等值而反向的反作用。
更为翔实的陈述是:
当两个物体相互作用时,作用在第一个物体上的力与作用在第二个物体上的力大小相等,方向相反。相对的力作用于同一条作用线上,并且属于同一类型,如接触力、摩擦力、引力或磁力。
当用球棒击球时,球棒对球的作用力与球对球棒的作用力大小相等,但这两个力的方向是相反的(由于球棒的质量比棒球大得多,因此根据牛顿第二定律,球的加速度比球棒大得多)。
第三定律不只适用于碰撞。当坐在椅子上时,我对椅子施加的向下的力等于椅子对我施加的向上的力。它也不仅仅适用于接触的物体。地球对苹果的引力和苹果对地球的引力一样大。
更一般地说,对于任何两个物体,它们之间的引力与它们质量的乘积成正比,与它们之间距离的平方成反比[或者更严格地说,与我们现在所说的它们质心之间距离的平方成反比(见图16)]。到1685年底,牛顿已经证明,他的三大运动定律和万有引力平方反比定律可以解释伽利略对地面物体运动的观察和开普勒对天体运动的观察。他还重拾了1666年的尝试:建立月球轨道与地月引力的估计强度之间的联系。这时地球半径已经有一个更准确的数字,于是他发现11%的差异消失了,计算结果与观测结果几乎完全一致。月球的惯性和地球的引力共同决定了月球的运动(牛顿指出,笛卡儿的以太旋涡不仅不必要,还与开普勒定律不相容)。
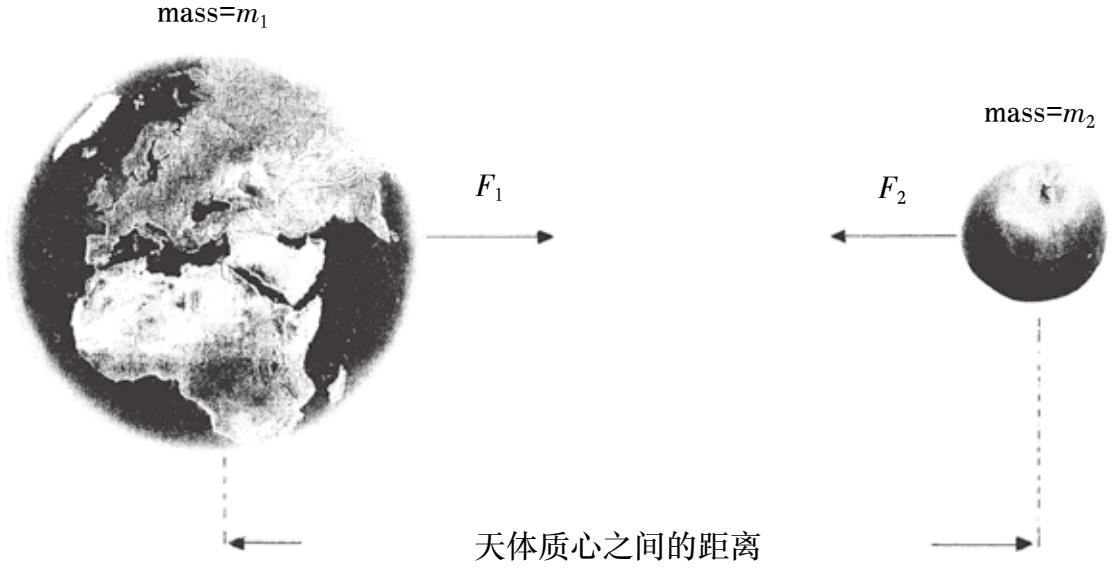
图16 牛顿的万有引力定律示意图
月球轨道与地球对月球引力的估计强度之间的相关性本身并不能证明引力是普遍的,也就是说,任意地方的任意两个物体都会相互吸引,其引力强度与它们的质量乘积成正比,与它们之间距离的平方成反比。但在他的《原理》第三卷中,牛顿证明了他的“万有引力定律”,可以连同他的运动定律来解释各种各样的观察结果:不仅仅是行星及其卫星简单明了的运动,还有大质量行星木星和土星接近合点时观察到的行星际扰动、太阳对月球运动的扰动作用、彗星的运动、潮汐现象、地球不完全是球形的事实(在赤道处隆起,在两极平坦),以及这种隆起的结果——分点岁差。
这个词指的是春分和秋分在时间上非常小但渐进的变化,我们现在知道这是由地轴的回旋造成的。回旋的角速度非常慢,完成一圈需要将近2.6万年。约公元前130年,希腊数学家喜帕恰斯(Hipparchus)在罗得岛编制星表时注意到,一颗名为“角宿一”(Spica)的恒星在秋分时的位置与亚历山大天文学家在大约一个半世纪前秋分时观察到的位置相差大约2°(天文经度)。喜帕恰斯把这种轻微的偏移归因于固定星整个外壳的缓慢运动。16个世纪后,哥白尼指出,如果行星运动的“日心说”理论是正确的,那么春秋分时间的轻微偏移就可以用地轴非常缓慢地回旋来解释。但地轴为什么会回旋呢?
牛顿回答了这个问题。图17展示了如果地轴确实回旋,需要考虑的3种地球运动。在图17中,阴影部分代表地球,赤道上的隆起和两极的扁平被大幅夸大了。从北极看去,地球在以日为周期逆时针旋转。自转轴并不垂直于地球每年绕太阳公转的轨道平面,而是从垂直方向倾斜约23°。倾斜方向在地球绕其轨道运行的过程中几乎保持不变,正是这一点导致了季节变化。尽管倾斜度保持不变,但地球相对于太阳的位置变化意味着北半球夏季时,(地轴北半部) 向太阳倾斜 ,北半球冬季时,(地轴北半部) 背离 太阳,而在春分或秋分时,它 不受影响 。当地轴的倾斜方向朝向或者背离太阳时,地球在赤道附近的隆起造成了太阳对地球分别位于轨道平面上方和下方两部分引力之间的微小差异,这些差异会产生轻微的扭力(或者说是转动力),从而减少地轴的倾斜度。月球的引力也导致了扭力。如果地球不旋转,这些扭力只会改变倾斜度,但是地球在旋转,因此,扭力的作用仿佛在试图改变一个旋转陀螺的倾斜度。它导致旋转的物体回旋——中轴非常缓慢地摇摆、画圈,就像在描画1个(或2个)圆锥体,其方向与旋转方向相反。正是地轴的这种缓慢运动——用了25 800年左右才转完一圈——导致了春秋分时间的微小但渐进而有规律的变化。
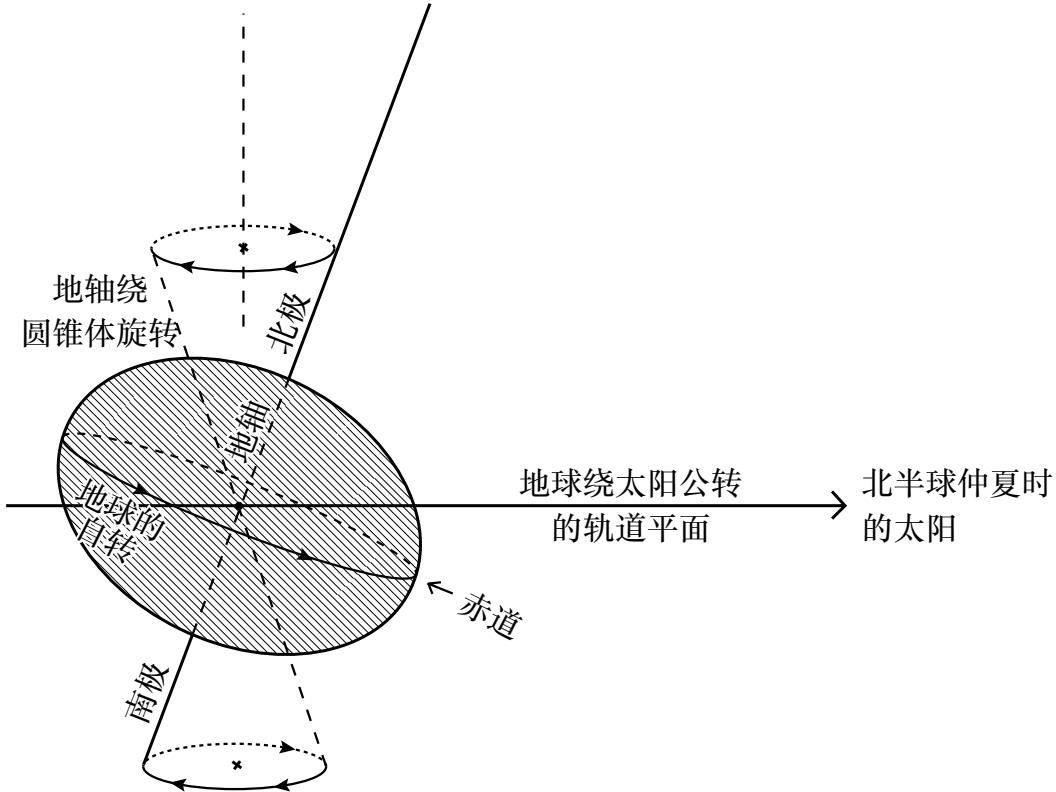
图17 地球的3种运动,即以日为周期的自转、以年为周期的公转和轴的回旋
牛顿的万有引力定律和三大运动定律的简单优雅和惊人广泛的解释能力一定给了他极大的满足感,但这项工作的一个方面却让他深感不快。在1693年2月写给三一学院院长理查德·本特利(Richard Bentley)的一封信中,他解释了原因:
不可思议的是,没有生命和理性的物质(在没有其他非物质介导的情况下)无须相互接触就能对其他物质产生作用和影响……这就是我希望你不要把内禀的引力归因于我的一个原因。引力对物质来说是固有和必不可少的,因此,一个物体可以通过真空远距离作用于另一个物体,而不需要任何其他事物的介导,不需要其他事物来依次传递它们的作用和力量,这样的想法对我来说是如此荒谬,我相信任何一个在哲学问题上有思考能力的人都不会轻信。引力必须由一个持续按照某些规律行事的动因引起,至于这个动因是物质的还是非物质的,我把这个问题留给我的读者。 [14]
幸运的是,随着时间的推移,物理学家已经完全能够接受远距离作用的概念,无论他们处理的是引力、电力还是磁力。正如马米恩(Marmion)的《古董收藏家》( The Antiquary )中的一个角色所说:“熟稔乃无畏之父。”
[1]
这就是后来被广泛用于歌剧眼镜的装置。不过,它的视野确实相当小,当伽利略试图向未经训练的使用者展示要看的东西时,时而会给他们增加难度。尽管如此,米尔顿在1638年拜访年迈的伽利略时,仍还是对这个设备大为欣赏,乃至在《失乐园》中写道:
……浑如球形的满月,
就是托斯卡纳那位大师透过望远镜所见,
夜晚时分,于飞索尔山顶,
或瓦达诺山谷,探望到的未经发现的土地,
还有江河与山峦,列布在那崎岖的球体上。


